Похожие презентации:
Теория игр. Платежная матрица. (Семинар 2)
1. Теория игр
Семинар 2:Теория игр
2. Платежная матрица
Пустьигрок A располагает m стратегиями
A1 , A2, …, Am и игрок B имеет n стратегий
B1 , B2, …, Bn.
Выигрыш игрока A при выборе стратегий
Ai и Bj обозначим aij.
Платежная матрица (матрица игры):
a11 a12 a1n
a 21 a22 a2 n
a
a
a
m2
mn
m1
3. Нижняя цена игры
Пустьαi – наименьший выигрыш игрока A
при выборе им стратегии Ai для всех
возможных стратегий игрока B:
i min ij
Тогда
j 1,n
гарантированный выигрыш игрока A
при любой стратегии игрока B равен:
max i max min ij
i 1, m
α – нижняя цена игры.
i 1, m
j 1, n
4. Верхняя цена игры
Числоβ – верхняя цена игры:
min max ij
j 1, n i 1,m
β
- гарантированный проигрыш игрока B.
Если
α = β = v, то v – чистая цена (или
цена игры). Тогда пара оптимальных
стратегий Ai и Bj, для которой aij = v
называется седловой точкой платежной
матрицы.
5. Задача 1
Найдите седловую точку в игре с матрицейвыигрышей А. В ответе указать чистую цену
игры.
0,1 0,4 0,2
А 0,5 0,4 0,3
0,3 0,2 0,1
6. Решение:
Найдем0,1 0,4 0,2
А 0,5 0,4 0,3
0,3 0,2 0,1
минимальные значения каждой
строки матрицы А и выберем из них
наибольшее для определения нижней
цены игры:
α1 = min (0,1; 0,4; 0,2) = 0,1
α2 = min (0,5; 0,4; 0,3) = 0,3
α3 = min (0,3; 0,2; 0,1) = 0,1
α = max (0,1; 0,3; 0,1) = 0,3
7.
0,1 0,4 0,2А 0,5 0,4 0,3
0,3 0,2 0,1
Найдем
верхнюю цену игры. Для этого
определим максимальное значение в
каждом столбце и выберем наименьшее из
них :
β1 = max (0,1; 0,5; 0,3) = 0,5
β2 = max (0,4; 0,4; 0,2) = 0,4
β3 = max (0,2; 0,3; 0,1) = 0,3
β = min (0,5; 0,4; 0,3) = 0,3
8.
0,1 0,4 0,2А 0,5 0,4 0,3
0,3 0,2 0,1
Получаем: α = β = 0,3
v = 0,3
Седловая точка - (A2B3)
9. Задача 2
Найдите седловую точку в игре с матрицейвыигрышей А. В ответе указать чистую цену
игры.
2 10 25 0
6
13 14 19
А
5 3 2 4
18 5 3 5
10. Решение:
Нижняя2 10 25 0
13 14 19 6
А
5 3 2 4
18 5 3 5
цена игры:
α1 = min (2; 10; 25; 0) = 0
α2 = min (13; 14; 19; 6) = 6
α3 = min (-5; 3; -2; -4) = - 5
α4 = min (18; 5; -3; -5) = - 5
α = max (0; 6 ; -5; -5) = 6
11.
2 10 25 013 14 19 6
А
5 3 2 4
18 5 3 5
Верхняя
цена игры:
β1 = max (2; 13; -5; 18) = 18
β2 = max (10; 14; 3; 5) = 14
β3 = max (25; 19; -2; -3) = 25
β4 = max (0; 6; -4; -5) = 6
β = min (18; 14 ; 25; 6) = 6
12.
2 10 25 013 14 19 6
А
5 3 2 4
18 5 3 5
Получаем: α = β = 6
v=6
Седловая точка - (A2B4)
13. Решение игры в смешанных стратегиях
Еслиα < β, то применение чистых стратегий
не дает оптимального решения игры.
Оптимальное решение можно получить
случайным образом путем чередования
чистых стратегий – в смешанных
стратегиях.
14.
Смешаннаястратегия SА игрока А –
применение чистых стратегий A1 , A2, …, Am с
вероятностями р1 , р2, …, рm.
A1
s A
p1
Для
A2 Am
p2 pm
m
p
i 1
i
1
игрока B аналогично:
B1
s B
q1
B2 Bn
q2 qn
n
q
j 1
j
1
15. Задача 3
Найдите решение игры в смешанныхстратегиях. В ответе указать среднюю цену
игры.
4 2
А
3 5
16. Решение:
Найдем4 2
А
3 5
нижнюю и верхнюю цену игры:
α = 3, β = 4, α ≠ β
Средний выигрыш игрока А равен цене
игры v, если он использует оптимальную
смешанную стратегию s*А A1 A 2
p*
1
p*2
игрок B использует чистую стратегию B1
(т.е. первый столбец платежной матрицы)
*
*
4 p1 3 p2 v
17.
Средний4 2
А
3 5
выигрыш игрока А также равен
цене игры v, если игрок B применяет
стратегию B2 (т.е. второй столбец
платежной матрицы):
2 p1* 5 p2* v
Получаем систему:
4 p1* 3 p2* v
*
*
2 p1 5 p2 v
p* p* 1
2
1
18.
Решаем4 2
А
3 5
систему:
4 p1* 3 p2* 2 p1* 5 p2*
*
*
p1 1 p2
*
*
4
p
3
p
v
1
2
4(1 p ) 3 p 2(1 p ) 5 p
*
*
p1 1 p2
*
*
1
*
4
p
3
p
v
1
2
p2 2
4 p2* 2 3 p2*
1
*
p1
*
*
2
p1 1 p2
7
4 p* 3 p* v
v
1
2
2
*
2
*
2
*
2
*
2
19.
Составим4 2
А
3 5
аналогичную систему для
игрока В:
4 q 2 q v
3q 5q v
q q* 1
2
*
1
*
1
*
1
4q 2q 3q 5q
*
*
3q1 5q2 v
*
*
q
1
q
1
2
*
2
*
2
*
1
*
2
4(1 q ) 2q 3(1 q ) 5q
*
*
3q1 5q2 v
*
*
q
1
q
1
2
*
2
*
2
*
2
*
1
*
2
*
2
* 1
q 2 4
3
*
q1
4
v 7
2
20.
4 2А
3 5
Ответ: pопт
1 1
3 1
7
( ; ), qопт ( ; ), v
2 2
4 4
2
21. Задача 4
Найдите решение игры в смешанныхстратегиях. В ответе указать среднюю цену
игры.
1,5 3
А
2 1
22. Решение:
Найдем1,5 3
А
2 1
нижнюю и верхнюю цену игры:
α = 1,5, β = 2, α ≠ β
23. Решение:
Найдем1,5 3
А
2 1
нижнюю и верхнюю цену игры:
α = 1,5, β = 2, α ≠ β
Система уравнений для игрока А:
1,5 p 2 p v
*
3 p p2 v
p p* 1
2
*
1
*
1
*
1
*
2
24.
1,5 p 2 p v*
3 p p2 v
p p* 1
2
*
1
*
1
*
1
*
2
* 3
p2 5
2
*
p1
5
v 9
5
1,5 3
А
2 1
25.
1,5 p 2 p v*
3 p p2 v
p p* 1
2
*
1
*
1
*
1
*
2
Составим
* 3
p2 5
2
*
p1
5
v 9
5
аналогичную систему для
игрока В:
1,5q 3q v
*
2 q q2 v
q q* 1
2
*
1
*
1
*
1
*
2
1,5 3
А
2 1
26.
1,5q 3q v*
2q q2 v
q q* 1
2
*
1
*
1
*
1
Ответ:
*
2
pопт
* 1
q2 5
4
*
q1
5
v 9
5
2 3
4 1
9
( ; ), qопт ( ; ), v
5 5
5 5
5
27. Задача 3
Найдите решение игры в смешанныхстратегиях графическим способом. В
ответе указать среднюю цену игры.
4 2
А
3 5
28. Решение:
Найдем4 2
А
3 5
нижнюю и верхнюю цену игры:
α = 3, β = 4, α ≠ β
29. Решение:
Найдем4 2
А
3 5
нижнюю и верхнюю цену игры:
α = 3, β = 4, α ≠ β
На оси Оx отложим единичный отрезок
A1A2.
Прямая x = 0 соответствует стратегии A1
игрока A, а прямая x = 1 соответствует
стратегии A2.
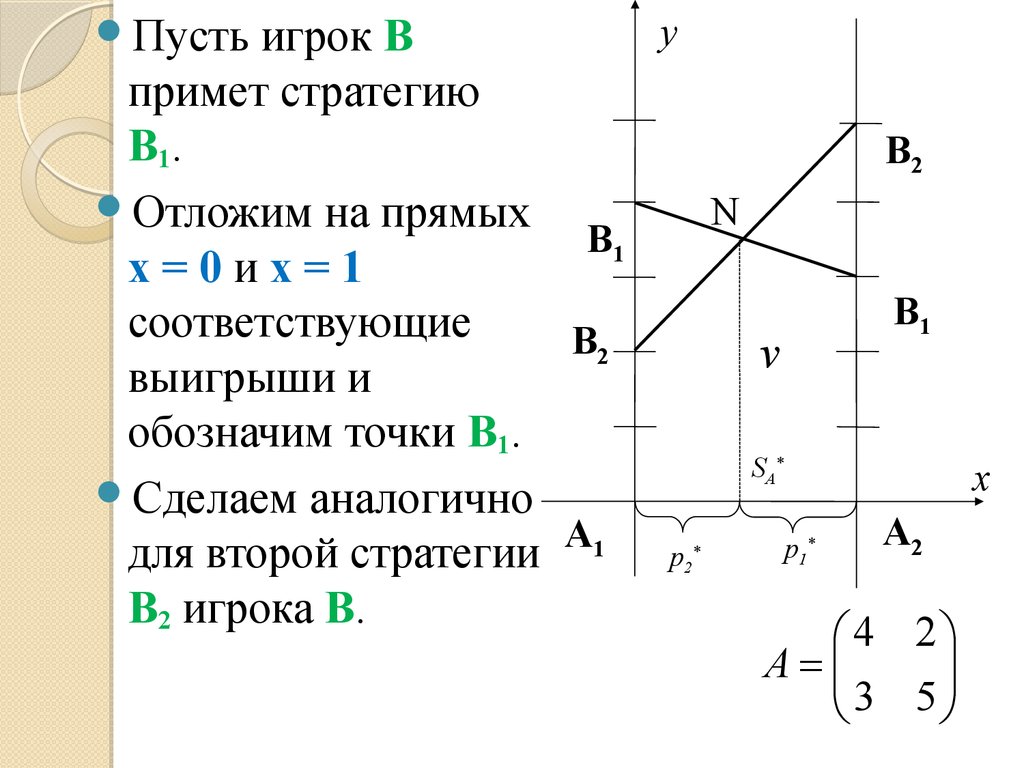
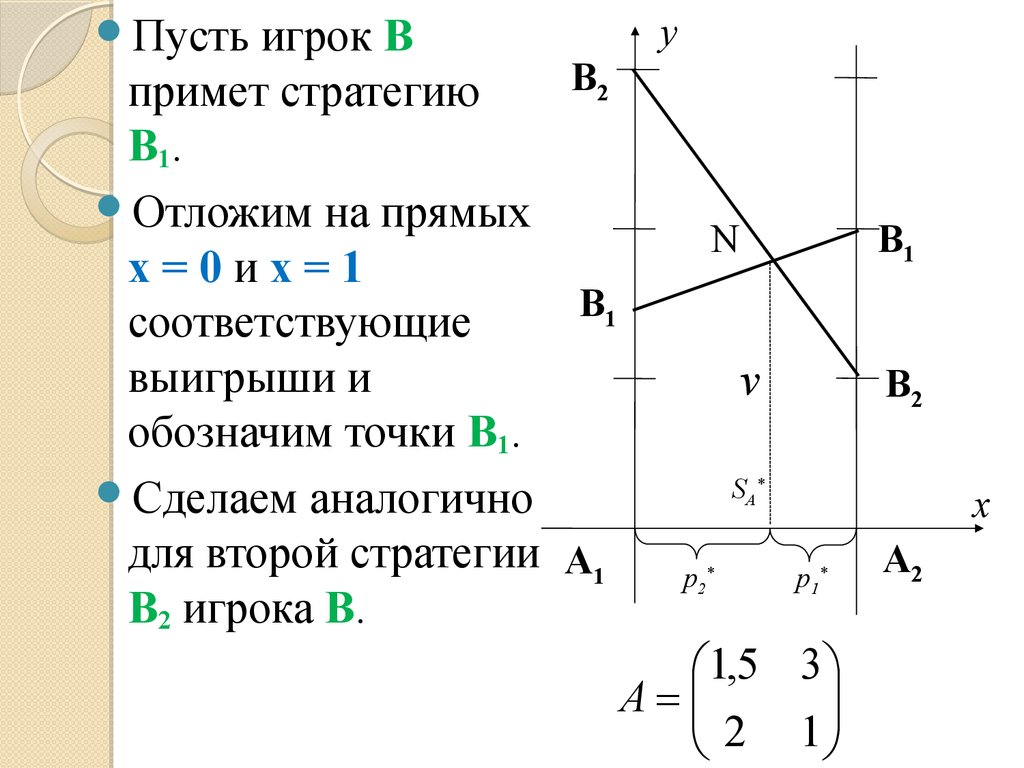
30.
yигрок В
примет стратегию
В1.
Отложим на прямых
N
В1
x=0иx=1
соответствующие
В2
v
выигрыши и
обозначим точки В1.
S
Сделаем аналогично
p
для второй стратегии А1 p
В2 игрока В.
Пусть
A
2
*
В2
В1
*
x
1
*
А2
4 2
А
3 5
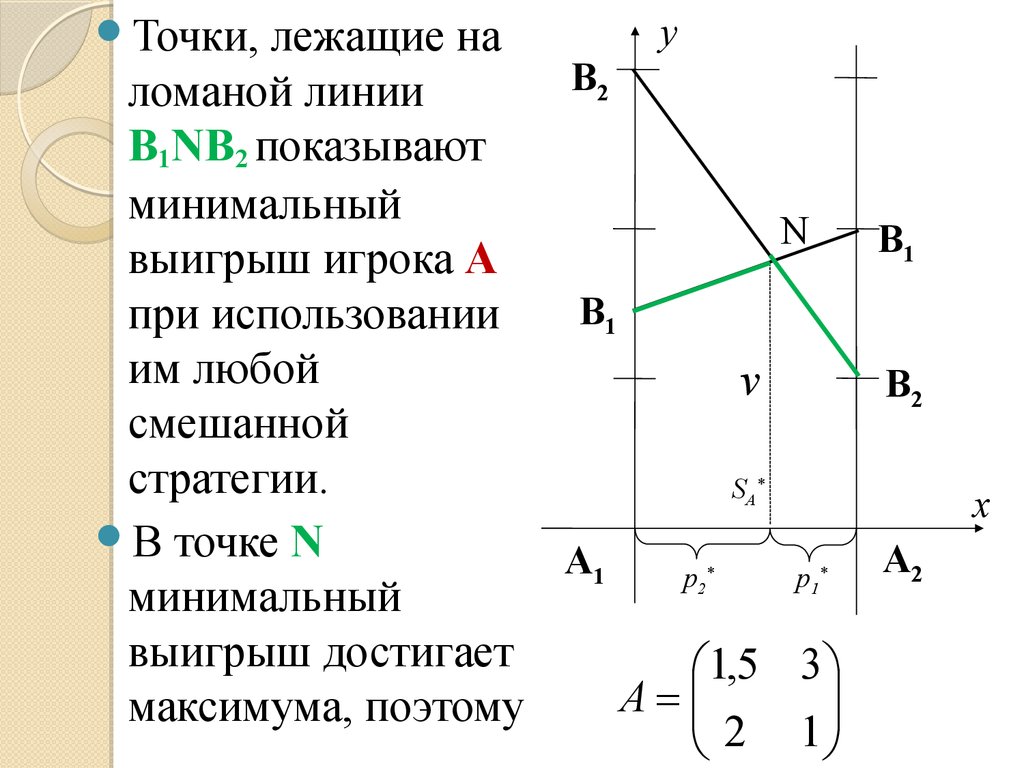
31.
лежащие наломаной линии
В2NВ1 показывают
минимальный
выигрыш игрока A
при использовании
им любой
смешанной
стратегии.
В точке N
минимальный
выигрыш достигает
максимума, поэтому
y
Точки,
В2
N
В1
В2
В1
v
S A*
А1
p2
*
x
p1*
А2
4 2
А
3 5
32.
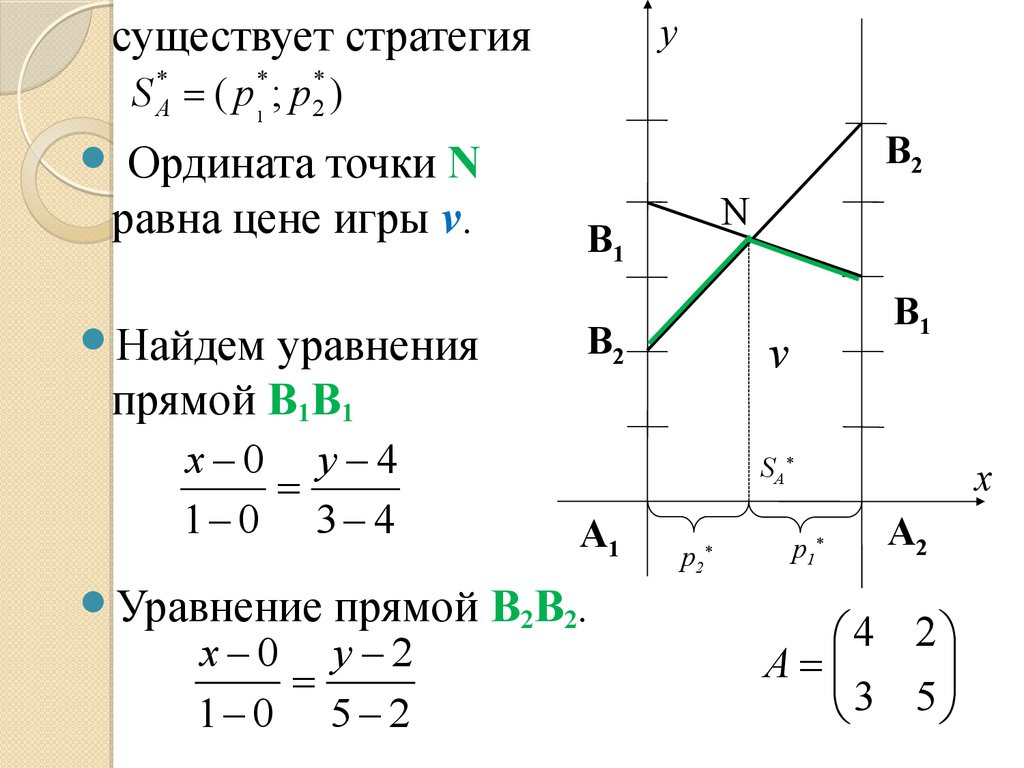
yсуществует стратегия
S A* ( p 1* ; p 2* )
Ордината точки N
равна цене игры v.
В2
Найдем
уравнения
прямой В1В1
x 0 y 4
1 0 3 4
Уравнение
В1
В2
В1
v
S A*
А1
прямой В2В2.
x 0 y 2
1 0 5 2
N
p2
*
p 1*
x
А2
4 2
А
3 5
33.
Получаем систему уравнений:y x 4
y 3x 2
1
p x
2
1
*
*
p1 1 p2
2
*
2
7
v y
2
1
x 2
7
y
2
34.
Определиманалогично геометрическим
способом оптимальную стратегию игрока
В.
Поменяем местами игроков А и В и вместо
максимума найдем минимум верхней
границы.
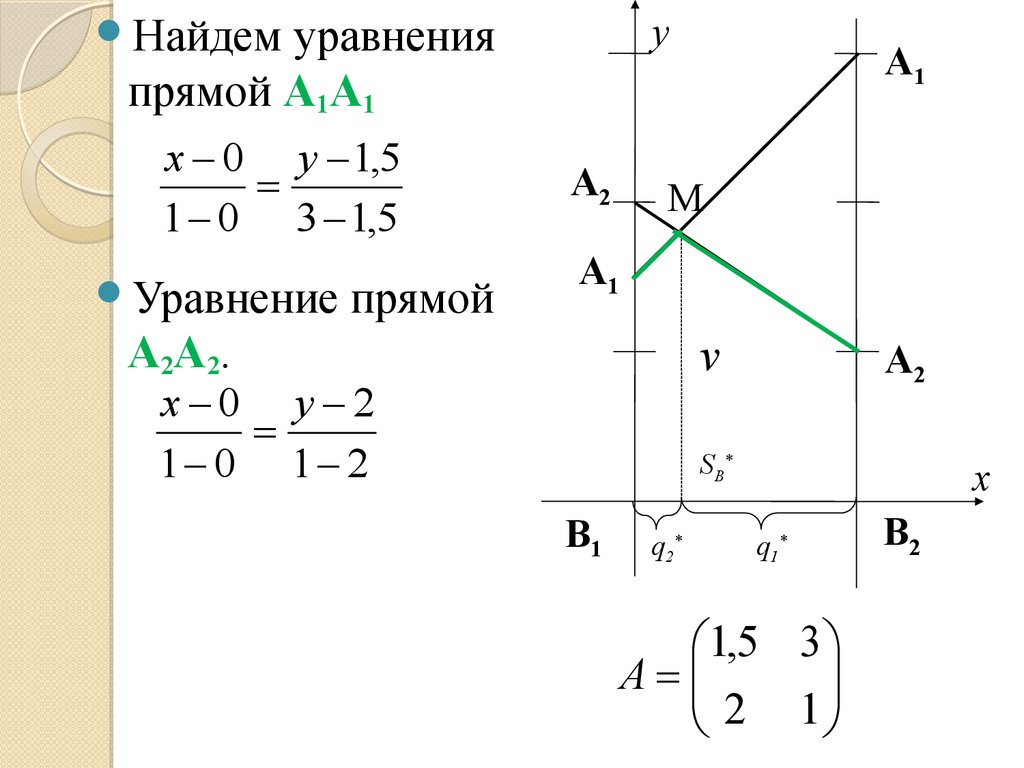
35.
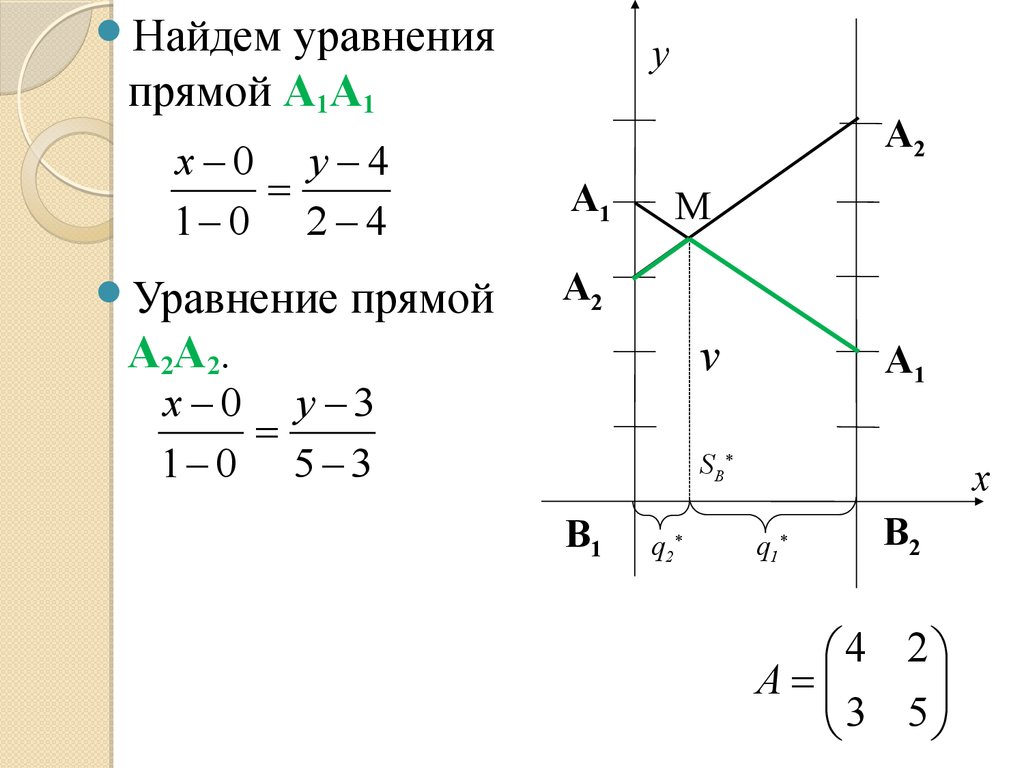
Найдемуравнения
прямой A1A1
x 0 y 4
1 0 2 4
Уравнение
прямой
y
А2
А1
M
А2
A2A2.
v
x 0 y 3
1 0 5 3
А1
S B*
В1
q2*
x
q1*
В2
4 2
А
3 5
36.
Получаемсистему уравнений:
y 2 x 4
y 2x 3
1
q x
4
3
*
*
q1 1 q2
4
1
x 4
7
y
2
*
2
7
v y
2
Ответ: pопт
1 1
3 1
7
( ; ), qопт ( ; ), v
2 2
4 4
2
37. Задача 4
Найдите решение игры в смешанныхстратегиях графическим способом. В
ответе указать среднюю цену игры.
1,5 3
А
2 1
38. Решение:
1,5 3Решение:
А
2 1
Найдем нижнюю и верхнюю цену игры:
α = 1,5, β = 2, α ≠ β
39. Решение:
1,5 3Решение:
А
2 1
Найдем нижнюю и верхнюю цену игры:
α = 1,5, β = 2, α ≠ β
На оси Оx отложим единичный отрезок
A1A2.
Прямая x = 0 соответствует стратегии A1
игрока A, а прямая x = 1 соответствует
стратегии A2.
40.
yигрок В
В2
примет стратегию
В1.
Отложим на прямых
N
В1
x=0иx=1
В1
соответствующие
выигрыши и
v
В2
обозначим точки В1.
S
Сделаем аналогично
для второй стратегии А1
А2
p
p
В2 игрока В.
1,5 3
А
2 1
Пусть
A
*
2
*
1
*
x
41.
yлежащие на
В2
ломаной линии
В1NВ2 показывают
минимальный
N
В1
выигрыш игрока A
В1
при использовании
им любой
v
В2
смешанной
стратегии.
S
В точке N
А2
А1
p
p
минимальный
выигрыш достигает
1,5 3
А
максимума, поэтому
2 1
Точки,
A
*
2
*
1
*
x
42.
существует стратегияS A* ( p 1* ; p 2* )
y
В2
Ордината точки N
равна цене игры v.
Найдем
уравнения
прямой В1В1
x 0 y 1,5
1 0 2 1,5
Уравнение
N
В1
v
В2
S A*
А1
прямой В2В2.
x 0 y 3
1 0 1 3
В1
p2*
x
p1*
1,5 3
А
2 1
А2
43.
Получаемсистему уравнений:
y 0,5 x 1,5
y 2 x 3
3
p x
5
2
*
*
p1 1 p2
5
*
2
9
v y
5
3
x 5
9
y
5
44.
Определиманалогично геометрическим
способом оптимальную стратегию игрока
В.
Поменяем местами игроков А и В и вместо
максимума найдем минимум верхней
границы.
45.
yНайдем
уравнения
прямой A1A1
x 0 y 1,5
1 0 3 1,5
Уравнение
прямой
А2
А1
M
А1
A2A2.
v
x 0 y 2
1 0 1 2
А2
S B*
В1
q2*
x
q1*
1,5 3
А
2 1
В2
46.
Получаемсистему уравнений:
y 1,5 x 1,5
y x 2
1
q x
5
4
*
*
q1 1 q2
5
1
x 5
9
y
5
*
2
9
v y
5
Ответ:
pопт
2 3
4 1
9
( ; ), qопт ( ; ), v
5 5
5 5
5
47. Доминирующие и доминируемые стратегии
Еслив платежной матрице A все элементы
i-й строки не меньше соответствующих
элементов k-й строки, aij ≥ akj , j = 1, 2, …,
n, а по крайней мере один строго больше,
то i-я строка – доминирующая, а k-я
строка – доминирумая.
48. Доминирующие и доминируемые стратегии
ИгрокуА не выгодно применять стратегии,
которым соответствуют доминируемые
строки, а игроку В – доминирующие
столбцы.
При решении игры можно уменьшить
размер платежной матрицы с помощью
удаления из нее доминируемых строк и
доминирующих столбцов.
49. Задача 5
Найти решение игры в смешанныхстратегиях, предварительно упростив ее.
В ответе указать среднюю цену игры.
2 4 3 2
А 4 3 2 6
3 2 1 3
50. Решение:
Найдем2 4 3 2
А 4 3 2 6
3 2 1 3
нижнюю и верхнюю цену игры:
α = 2, β = 3, α ≠ β
51. Решение:
Найдем2 4 3 2
А 4 3 2 6
3 2 1 3
нижнюю и верхнюю цену игры:
α = 2, β = 3, α ≠ β
Cтрока А3 доминируемая относительно
строки А1, поэтому для игрока А она не
выгодна.
Для игрока В не выгодны столбцы В1 и В2 .
52.
2 4 3 2А 4 3 2 6
3 2 1 3
Удаляем
не выгодные для игроков А и В
стратегии и получаем матрицу:
3 2
А
2 6
Решим
полученную задачу аналитическим
способом. Для игрока А:
53.
2 4 3 2А 4 3 2 6
3 2 1 3
Удаляем
не выгодные для игроков А и В
стратегии и получаем матрицу:
3 2
А
2 6
Решим
полученную задачу аналитическим
способом. Для игрока А:
3 p1* 2 p2* v
*
*
2 p1 6 p2 v
p* p* 1
1
2
54.
3 p1* 2 p2* 2 p1* 6 p2**
*
3 p1 2 p2 v
*
*
p1 1 p2
3 2
А
2 6
3(1 p2* ) 2 p2* 2(1 p2* ) 6 p2*
*
*
3 p1 2 p2 v
*
*
5
p
1
p
*
1
2
3 p2* 2 8 p2*
*
*
3 p1 2 p2 v
p* 1 p*
1
2
p2 9
4
*
p1
9
v 22
9
55.
Дляигрока В:
3q1* 2q2* v
*
*
2q1 6q2 v
q* q* 1
2
1
3 2
А
2 6
56.
Для3 2
А
2 6
игрока В:
3q1* 2q2* v
*
*
2q1 6q2 v
q* q* 1
2
1
3 5q 2 4q
*
*
2q1 6q2 v
q* 1 q*
1
2
*
2
3q1* 2q2* 2q1* 6q2*
*
*
2q1 6q2 v
*
*
q
1
q
1
2
*
2
* 1
q2 9
8
*
q1
9
v 22
9
57.
2 4 3 2А 4 3 2 6
3 2 1 3
Ответ:
pопт
4 5
8 1
22
( ; ;0), qопт (0;0; ; ), v
9 9
9 9
9
58. Задача 6
Найти решение игры в смешанныхстратегиях, предварительно упростив ее.
В ответе указать среднюю цену игры.
7
5
А
5
2
6 5 4 2
4 3 2 3
6 6 3 5
3 3 2 4
59. Решение:
Найдем7
5
А
5
2
6 5 4 2
4 3 2 3
6 6 3 5
3 3 2 4
нижнюю и верхнюю цену игры:
α = 3, β = 4, α ≠ β
60. Решение:
Найдем7
5
А
5
2
6 5 4 2
4 3 2 3
6 6 3 5
3 3 2 4
нижнюю и верхнюю цену игры:
α = 3, β = 4, α ≠ β
Строка А2 доминируемая относительно
строки А1 .
Строка А4 доминируемая строки А3.
Для игрока А они не выгодны.
7 6 5 4 2
Остается матрица: А
5 6 6 3 5
61.
7 6 5 4 2А
5 6 6 3 5
Для игрока В при сравнении:
В1 и В4 исключим столбец В1;
В2 и В4 исключим столбец В2;
В3 и В4 исключим столбец В3.
4 2
Остается матрица: А
3 5
62.
4 2А
3 5
Решим полученную задачу аналитическим
способом. Для игрока А:
4 p1* 3 p2* v
*
*
2 p1 5 p2 v
p* p* 1
2
1
63.
4 2А
3 5
4 p 3 p v
2 p 5 p v
p p* 1
2
*
1
*
1
*
1
Для
*
2
*
2
игрока В:
* 1
p2 2
1
*
p1
2
v 7
2
64.
4 2А
3 5
4 p 3 p v
2 p 5 p v
p p* 1
2
*
1
*
1
*
1
*
2
*
2
Для
игрока В:
4 q 2 q v
3q 5q v
q q* 1
2
*
1
*
1
*
1
*
2
*
2
* 1
p2 2
1
*
p1
2
v 7
2
65.
4q1* 2q2* v*
*
3q1 5q2 v
q* q* 1
2
1
* 1
q 2 4
3
*
q1
4
v 7
2
Ответ:
pопт
1 1
3 1
7
( ;0; ;0), qопт (0;0;0; ; ), v
2 2
4 4
2
7
5
А
5
2
6 5 4 2
4 3 2 3
6 6 3 5
3 3 2 4
4 2
А
3 5
66. Приведение матричной игры к задаче линейного программирования
Пустьигрок A обладает Ai стратегиями
i = 1, 2, …, m и игрок B имеет Bj стратегий
j = 1, 2, …, n.
Оптимальная стратегия SA* обеспечивает
игроку A при любой стратегии игрока B
средний выигрыш, не меньший, чем цена
игры v, и при оптимальной стратегии
игрока B выигрыш равный цене игры v.
67.
Пустьv > 0, тогда для оптимальной
стратегии SA* все средние выигрыши не
меньше цены игры v:
a11 p1 a21 p2 ... am1 p m v
a p a p ... a p v
12 1
22 2
m2 m
a1n p1 a2 n p2 ... amn pm v
Пусть
pj
x j , тогда:
v
a11 x1 a21 x2 ... am1 xm 1
a x a x ... a x 1
12 1 22 2
m2 m
a1n x1 a2 n x2 ... amn xm 1
68.
Цельигрока A – максимизировать свой
гарантированный выигрыш.
Рассмотрим
m
m
x
j 1
j
j 1
pj
1 m
1
pj
v v j 1
v
Поскольку
m
v max , то x j min
j 1
69.
Получаемзадачу линейного
программирования:
f x1 x2 ... xm min
a x a x ... a x 1
m1 m
11 1 21 2
a12 x1 a22 x2 ... am 2 xm 1
a1n x1 a2 n x2 ... amn xm 1
x1 0, x2 0,..., xm 0
Решением
задачи будет оптимальная
стратегия SA* игрока A.
70.
Дляопределения оптимальной стратегии
SВ*игрока B следует учесть, что игрок B
стремится минимизировать гарантированный
выигрыш игрока A.
Тогда задача линейного программирования
будет иметь вид:
y1 y2 ... yn max
a y a y ... a y 1
1n n
11 1 12 2
a21 y1 a22 y2 ... a2 n yn 1
am1 y1 am 2 y2 ... amn yn 1
y1 0, y2 0,..., ym 0
где
yj
qj
v
71. Задача 7
Найти решение игры с помощьюлинейного программирования.
1 2 0
А 1 0 1
2 1 0
72. Решение:
Найдем1 2 0
А 1 0 1
2 1 0
нижнюю и верхнюю цену игры:
α = 0, β = 1, α ≠ β
73. Решение:
Найдем1 2 0
А 1 0 1
2 1 0
нижнюю и верхнюю цену игры:
α = 0, β = 1, α ≠ β
Решим задачу для второго игрока В с
помощью линейного программирования:
y1 y2 y3 max
y 2y 1
2
1
y1 y3 1
2 y y 1
2
1
y1 0, y2 0, y3 0
где
yj
qj
v
74.
y1 y2 y3 maxy 2y 1
2
1
y1 y3 1
2 y y 1
2
1
y1 0, y2 0, y3 0
Приведем
1 2 0
А 1 0 1
2 1 0
полученную систему к
каноническому виду:
y1 y2 y3 max
y1 2 y2 y4 1
y1 y3 y5 1
2 y y y 1
2
6
1
yi 0, i 1,6
75.
y1 y2 y3 maxy1 2 y2 y4 1
y1 y3 y5 1
2 y y y 1
2
6
1
yi 0, i 1,6
1 2 0
А 1 0 1
2 1 0
y1 y2 y3 0
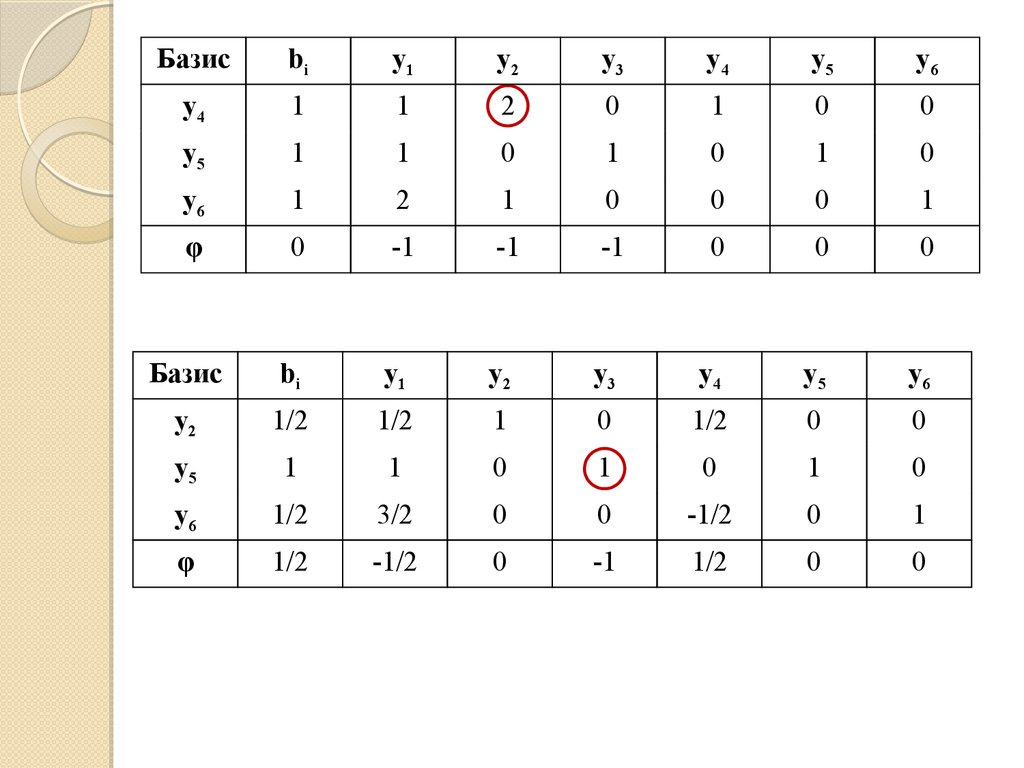
Решим
полученную задачу линейного
программирования симплекс-методом:
Базис
bi
y1
y2
y3
y4
y5
y6
y4
1
1
2
0
1
0
0
y5
1
1
0
1
0
1
0
y6
1
2
1
0
0
0
1
φ
0
-1
-1
-1
0
0
0
1 1 1
min ;
2 1 2
76.
Базисbi
y1
y2
y3
y4
y5
y6
y4
1
1
2
0
1
0
0
y5
1
1
0
1
0
1
0
y6
1
2
1
0
0
0
1
φ
0
-1
-1
-1
0
0
0
Базис
bi
y1
y2
y3
y4
y5
y6
y2
1/2
1/2
1
0
1/2
0
0
y5
1
1
0
1
0
1
0
y6
1/2
3/2
0
0
-1/2
0
1
φ
1/2
-1/2
0
-1
1/2
0
0
77.
Базисbi
y1
y2
y3
y4
y5
y6
y2
1/2
1/2
1
0
1/2
0
0
y5
1
1
0
1
0
1
0
y6
1/2
3/2
0
0
-1/2
0
1
φ
1/2
-1/2
0
-1
1/2
0
0
Базис
bi
y1
y2
y3
y4
y5
y6
y2
1/2
1/2
1
0
1/2
0
0
y3
1
1
0
1
0
1
0
y6
1/2
3/2
0
0
-1/2
0
1
φ
3/2
1/2
0
0
1/2
1
0
3
1
y 0; ;1 , max
2
2
*
78.
Поскольку y jqj
v
и
q1 q2 q3 1
1
y1 y 2 y3
q1 q2 q3
v
v
v v
v
то
2
v
3
2
q y v 0 0
3
*
1
*
1
1 2 1
q y v
2 3 3
2 2
*
*
q3 y3 v 1
3 3
*
2
*
2
3
1
y * 0; ;1 , max
2
2
79.
Базисbi
y1
y2
y3
y4
y5
y6
y2
1/2
1/2
1
0
1/2
0
0
y3
1
1
0
1
0
1
0
y6
1/2
3/2
0
0
-1/2
0
1
φ
3/2
1/2
0
0
1/2
1
0
1 2 1
p x v
2 3 3
*
1
*
1
v
2
3
2 2
p x v 1
3 3
2
*
*
p3 x3 v 0 0
3
*
2
*
2
Ответ:
pопт
2
1 2
1 2
0; ; , qопт ; ;0 , v
3
3 3
3 3
80. Задача 8
Найти решение игры с помощьюлинейного программирования.
4 6 3
А 9 5 4
7 3 6
81. Решение:
Найдем4 6 3
А 9 5 4
7 3 6
нижнюю и верхнюю цену игры:
α = 4, β = 6, α ≠ β
82. Решение:
Найдем4 6 3
А 9 5 4
7 3 6
нижнюю и верхнюю цену игры:
α = 4, β = 6, α ≠ β
Решим задачу для второго игрока В с
помощью линейного программирования:
y1 y2 y3 max
4 y 6 y 3 y 1
2
3
1
9 y1 5 y2 4 y3 1
7 y 3 y 6 y 1
2
3
1
y1 0, y2 0, y3 0
где
yj
qj
v
83.
y1 y2 y3 max4 y 6 y 3 y 1
2
3
1
9 y1 5 y2 4 y3 1
7 y 3 y 6 y 1
2
3
1
y1 0, y2 0, y3 0
Приведем
полученную систему к
каноническому виду:
y1 y2 y3 max
4 y1 6 y2 3 y3 y4 1
9 y1 5 y2 4 y3 y5 1
7 y 3 y 6 y y 1
2
3
6
1
yi 0, i 1,6
4 6 3
А 9 5 4
7 3 6
84.
y1 y2 y3 max4 y1 6 y2 3 y3 y4 1
9 y1 5 y2 4 y3 y5 1
7 y 3 y 6 y y 1
2
3
6
1
yi 0, i 1,6
Решим
y1 y2 y3 0
симплекс-методом:
Базис
bi
y1
y2
y3
y4
y5
y6
y4
1
4
6
3
1
0
0
y5
1
9
5
4
0
1
0
y6
1
7
3
6
0
0
1
φ
0
-1
-1
-1
0
0
0
1 1 1 1
min ; ;
4 9 7 9
85.
Базисbi
y1
y2
y3
y4
y5
y6
y4
1
4
6
3
1
0
0
y5
1
9
5
4
0
1
0
y6
1
7
3
6
0
0
1
φ
0
-1
-1
-1
0
0
0
Базис
bi
y1
y2
y3
y4
y5
y6
y4
5/9
0
34/9
11/9
1
-4/9
0
y1
1/9
1
5/9
4/9
0
1/9
0
y6
2/9
0
-8/9
26/9
0
-7/9
1
φ
1/9
0
-4/9
-5/9
0
1/9
0
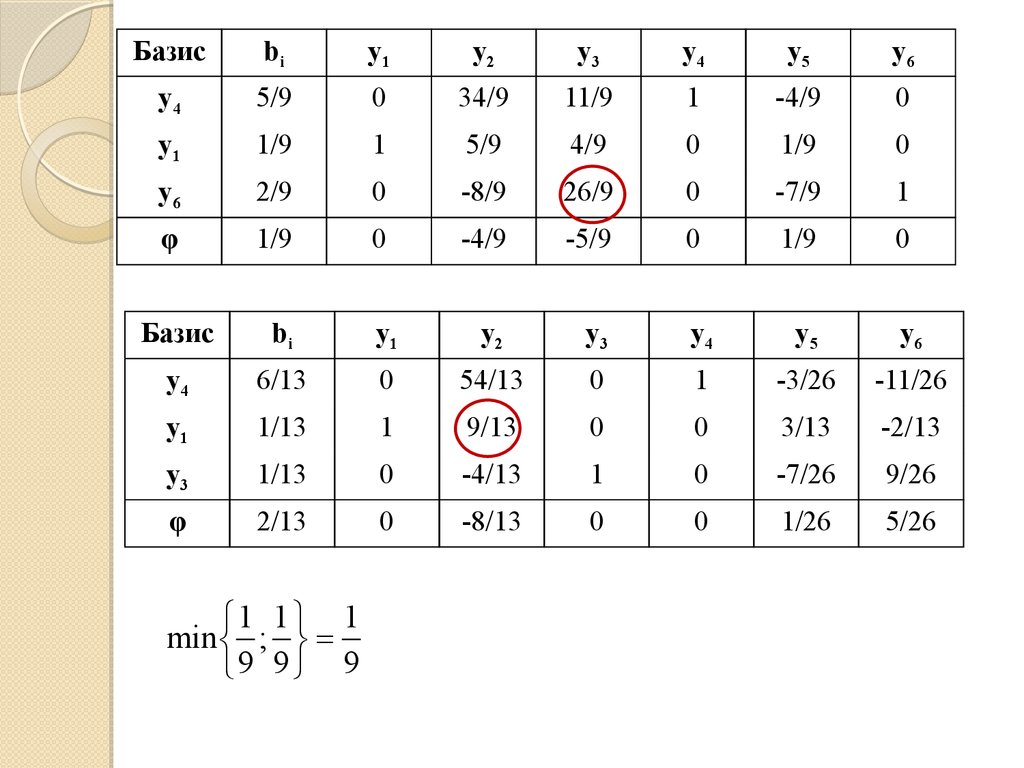
5 1 1 1
min ; ;
11 4 13 13
86.
Базисbi
y1
y2
y3
y4
y5
y6
y4
5/9
0
34/9
11/9
1
-4/9
0
y1
1/9
1
5/9
4/9
0
1/9
0
y6
2/9
0
-8/9
26/9
0
-7/9
1
φ
1/9
0
-4/9
-5/9
0
1/9
0
Базис
bi
y1
y2
y3
y4
y5
y6
y4
6/13
0
54/13
0
1
-3/26
-11/26
y1
1/13
1
9/13
0
0
3/13
-2/13
y3
1/13
0
-4/13
1
0
-7/26
9/26
φ
2/13
0
-8/13
0
0
1/26
5/26
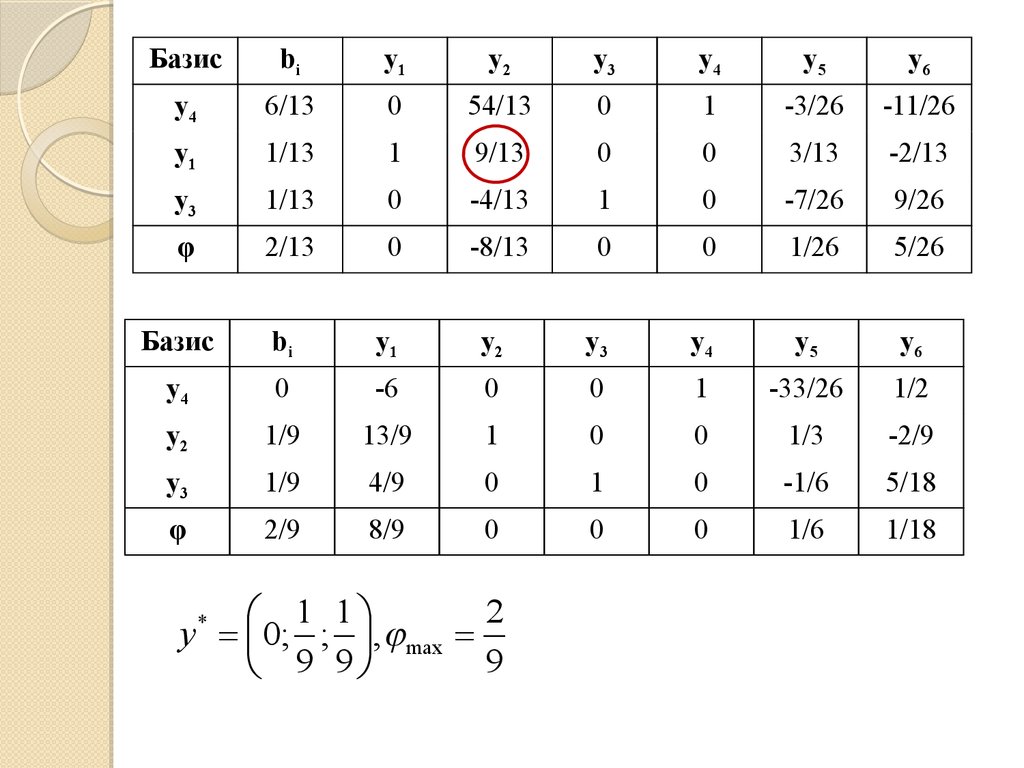
1 1 1
min ;
9 9 9
87.
Базисbi
y1
y2
y3
y4
y5
y6
y4
6/13
0
54/13
0
1
-3/26
-11/26
y1
1/13
1
9/13
0
0
3/13
-2/13
y3
1/13
0
-4/13
1
0
-7/26
9/26
φ
2/13
0
-8/13
0
0
1/26
5/26
Базис
bi
y1
y2
y3
y4
y5
y6
y4
0
-6
0
0
1
-33/26
1/2
y2
1/9
13/9
1
0
0
1/3
-2/9
y3
1/9
4/9
0
1
0
-1/6
5/18
φ
2/9
8/9
0
0
0
1/6
1/18
2
1 1
y 0; ; , max
9
9 9
*
88.
Поскольку y jqj
v
и
q1 q2 q3 1
1
y1 y 2 y3
q1 q2 q3
v
v
v v
v
то
9
v
2
9
q y v 0 0
2
1 9 1
*
*
q2 y 2 v
9 2 2
1 9 1
*
*
q3 y3 v
9 2 2
*
1
*
1
2
1 1
y 0; ; , max
9
9 9
*
89.
Базисbi
y1
y2
y3
y4
y5
y6
y4
0
-6
0
0
1
-33/26
1/2
y2
1/9
13/9
1
0
0
1/3
-2/9
y3
1/9
4/9
0
1
0
-1/6
5/18
φ
2/9
8/9
0
0
0
1/6
1/18
9
p x v 0 0
2
*
1
*
1
9
v
2
1 9 3
p x v
6 2 4
1 9 1
*
*
p3 x3 v
18 2 4
*
2
*
2
Ответ:
pопт
9
3 1
1 1
0; ; , qопт 0; ; , v
2
4 4
2 2
90. Игра с природой
- матричная игра, где игрок взаимодействуетс окружающей средой, которая не
заинтересована в его проигрыше, и решает
задачу определения оптимальной стратегии
с учетом неопределенности состояния
окружающей среды.
91. Игра с природой
Пусть A1 , A2,…, Am - возможные чистые
стратегии игрока A; П1 , П2, …, Пn –
возможные состояния природы; aij –
выигрыш игрока при применении им своей
i-й стратегии при j-м состоянии природы.
Платежная матрица:
a11
a21
А
a
m1
П1
a12
a22
am 2
a1n А1
a2 n А 2
amn А m
П2 Пn
92.
Естьдругой способ задания матрицы игры с
природой – в виде матрицы рисков R rij
Риск rij игрока A при использовании
стратегии Ai и состоянии природы Пj –
разность между выигрышем, который
получил бы игрок, если бы знал, что
состоянием природы будет Пj, и
выигрышем, который получит игрок, не
зная этого.
rij max aij aij
1 i m
93.
Дляопределения оптимальной стратегии
игрока A в игре с природой используется ряд
критериев: Лапласа, Вальда, Сэвиджа, Гурвица.
Критерий
Вальда – основан на выборе
наилучшей из наихудших стратегий Ai.
Если в матрице А результат аij представляет
выигрыш игрока A, при выборе его
оптимальной стратегии используется
максиминный критерий:
Z max min aij
1 i m 1 j n
94.
КритерийCэвиджа – использует матрицу
рисков
R rij ; i 1, m; j 1, n
В
оптимальной стратегии минимизируется
максимальный риск (достигается значение
S):
S min max rij
1 i m 1 j n
95.
КритерийГурвица – при любом выборе
стратегии наихудший для игрока А вариант
реализуется с вероятностью α, а наилучший
с вероятностью 1-α,
где α – показатель пессимизма (0 ≤ α ≤ 1).
Если аij – выигрыш игрока А, то
оптимальной стратегией считается та, в
которой достигается значение G:
S max( min aij (1 ) max aij )
1 i m
1 j n
1 j n
96.
КритерийЛапласа – все состояния
природы Пj, j = 1, …, n, считаются
равновероятностными q j 1 .
n
Оптимальной стратегией считается та, для
которой достигается значение L:
1 n
S max aij
1 i m n
j 1
97. Задача 9
Найти оптимальную стратегию игрока, используякритерии оптимальности Вальда, Гурвица,
Сэвиджа, Лапласа (коэффициент пессимизма равен
0,3).
2 3 4
А 1 1 1
3 4 1
98. Решение:
2 3 4А 1 1 1
3 4 1
1. Найдем критерий Вальда.
В каждой строке матрицы найдем
наименьший элемент, а затем из них
выберем строку j с наибольшим из
найденных элементов:
Z1 min(2;3; 4) 4
Z 2 min( 1;1;1) 1
Z 3 min(3;4; 1) 1
Z max( 4; 1; 1) 1
По критерию Вальда оптимальные
стратегии A2 и A3.
99.
2 3 4А 1 1 1
3 4 1
2. Найдем критерий Сэвиджа.
Для матрицы А построим матрицу рисков R:
4 3 1 ( 4) 1 1 5
3 2
R 3 ( 1) 4 1
1 1 4 3 0
3 3
0 0 2
4
4
1
(
1
)
В каждом столбце выбираем наибольший
элемент: 3; 4; 1
100.
4 3 1 ( 4) 1 1 53 2
R 3 ( 1) 4 1
1 1 4 3 0
3 3
0 0 2
4
4
1
(
1
)
Найдем наибольший элемент каждой строки
матрицы R, затем среди них выберем
минимальный.
S1 max(1;1;5) 5
S 2 max(4;3;0) 4
S3 max(0;0;2) 2
S3 min(5;4;2) 2
По критерию Сэвиджа оптимальная стратегия
A3.
101.
2 3 4А 1 1 1
3 4 1
3. Найдем критерий Гурвица. (α = 0,3)
G1 0,3 ( 4) 0,7 3 0,9
G2 0,3 ( 1) 0,7 1 0,4
G3 0,3 ( 1) 0,7 4 2,5
G max(0,9;0,4;2,5) 2,5
По
критерию Гурвица оптимальная
стратегия A3.
102.
2 3 4А 1 1 1
3 4 1
4. Найдем критерий Лапласа. n = 3
1
1
L1 (2 3 4)
3
3
1
1
L2 ( 1 1 1)
3
3
1
L3 (3 4 1) 2
3
1 1
L max( ; ;2) 2
3 3
По
критерию Лапласа оптимальная
стратегия A3.
103.
Ответ:По критерию Вальда оптимальные
стратегии A2 и A3.
По критерию Сэвиджа оптимальная
стратегия A3.
По критерию Гурвица оптимальная
стратегия A3.
По критерию Лапласа оптимальная
стратегия A3.
104. Задача 10
Найти оптимальную стратегию игрока, используякритерии оптимальности Вальда, Гурвица,
Сэвиджа, Лапласа (коэффициент пессимизма равен
0,3).
8 4 7
А 6 5 9
7 7 8
105. Решение:
8 4 7А 6 5 9
7 7 8
1. Найдем критерий Вальда.
В каждой строке матрицы найдем
наименьший элемент, а затем из них
выберем строку j с наибольшим из
найденных элементов:
Z1 min(8;4;7) 4
Z 2 min(6;5;9) 5
Z 3 min(7;7;8) 7
Z max(4;5;7) 7
По критерию Вальда оптимальные
стратегии A3.
106.
8 4 7А 6 5 9
7 7 8
2. Найдем критерий Сэвиджа.
Для матрицы А построим матрицу рисков R:
8 8 7 4 9 7 2 3 2
R 8 6 7 5 9 9 2 2 0
8 7 7 7 9 8 1 0 1
В каждом столбце выбираем наибольший
элемент: 8; 7; 9
107.
8 8 7 4 9 7 2 3 2R 8 6 7 5 9 9 2 2 0
8 7 7 7 9 8 1 0 1
Найдем наибольший элемент каждой строки
матрицы R, затем среди них выберем
минимальный.
S1 max(2;3;2) 3
S 2 max(2;2;0) 2
S3 max(1;0;1) 1
S3 min(3;2;1) 1
По критерию Сэвиджа оптимальная стратегия
A3.
108.
8 4 7А 6 5 9
7 7 8
3. Найдем критерий Гурвица. (α = 0,3)
G1 0,3 4 0,7 8 6,8
G2 0,3 5 0,7 9 7,8
G3 0,3 7 0,7 8 7,7
G max(6,8;7,8;7,7) 7,8
По
критерию Гурвица оптимальная
стратегия A2.
109.
8 4 7А 6 5 9
7 7 8
4. Найдем критерий Лапласа. n = 3
1
19
L1 (8 4 7)
3
3
1
20
L2 (6 5 9)
3
3
1
22
L3 (7 7 8)
3
3
19 20 22
22
L max( ; ; )
3 3 3
3
По
критерию Лапласа оптимальная
стратегия A3.
110.
Ответ:По критерию Вальда оптимальная
стратегия A3.
По критерию Сэвиджа оптимальная
стратегия A3.
По критерию Гурвица оптимальная
стратегия A2.
По критерию Лапласа оптимальная
стратегия A3.



















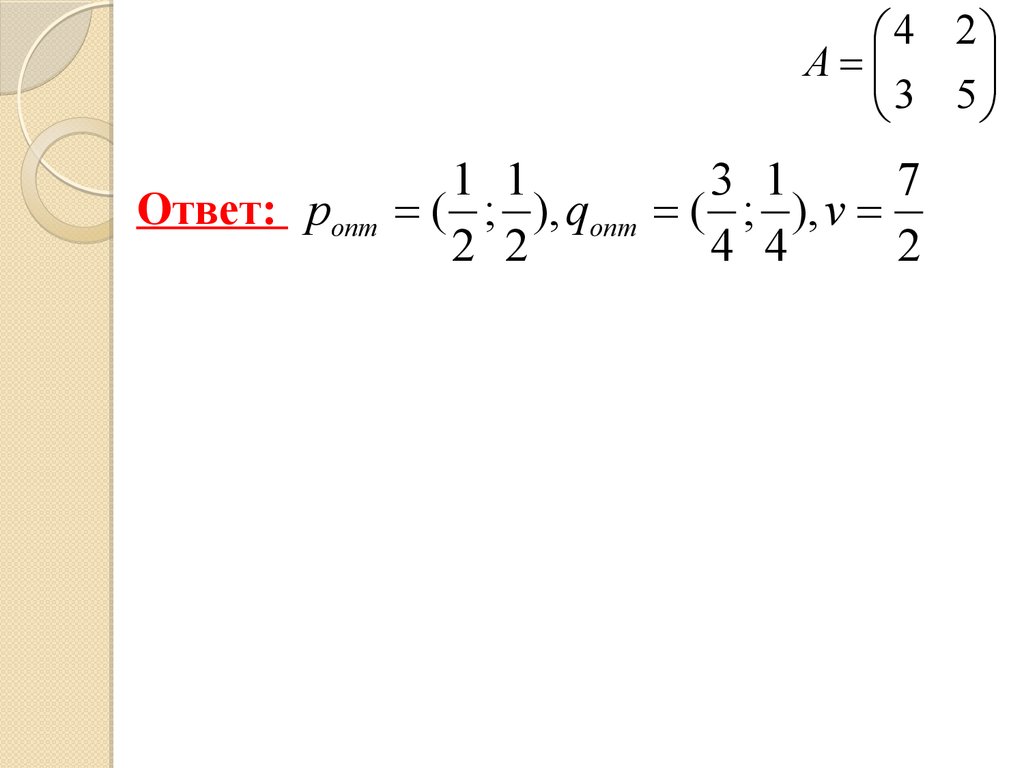



























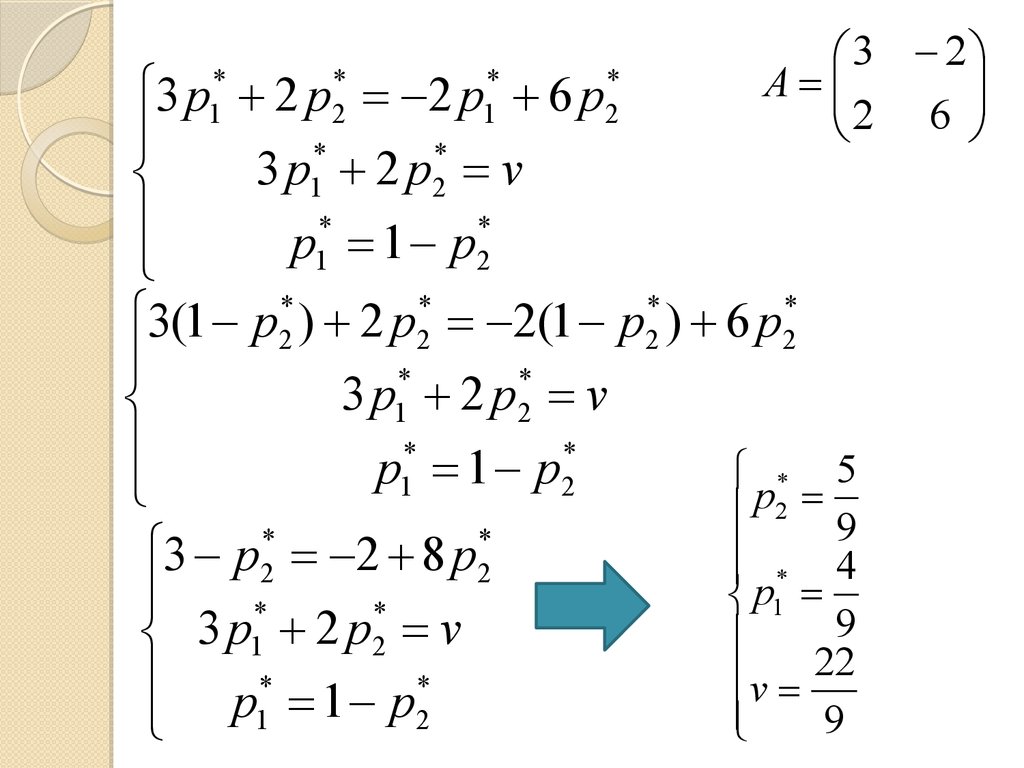






























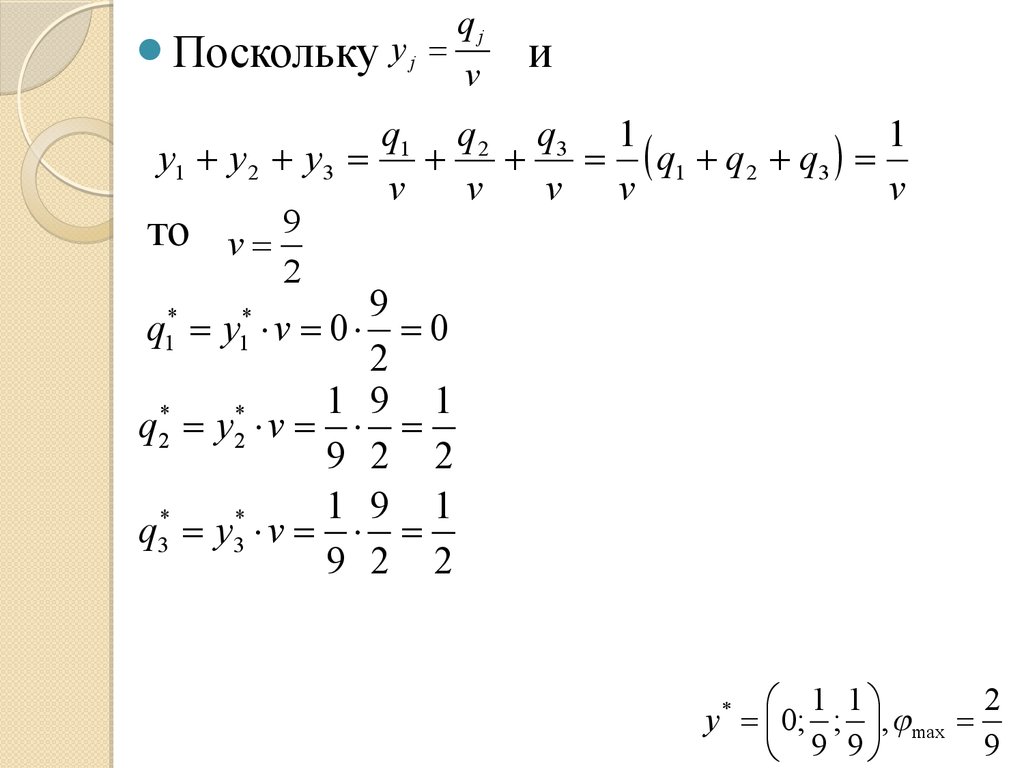























 Математика
Математика Программирование
Программирование








