Электротехника. Электрические фильтры. (Лекция 11)

1.

Кубанский государственный технологический университет
Институт информационных технологий и безопасности
Кафедра компьютерных технологий и информационной
безопасности
Учебная дисциплина
Электротехника
Лекция № 11
Электрические фильтры

2.

Учебные вопросы:
1. Определения и классификация электрических фильтров.
2. Достаточное условие работы классического фильтра в
полосе пропускания.
3. Фильтры нижних частот типа «k» и типа «m».
4. Полиномиальные фильтры.
5. Понятия об активных фильтрах.
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 169 –187.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 208 –
227.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.:
Высшая школа, 2003 г, с. 128 –132.

3.

1. Определения и классификация электрических фильтров.
Электрическим фильтром называется четырехполюсник, пропускающий
без ослабления или с малым ослаблением колебания определенных частот
и пропускающий с большим ослаблением колебания других частот.
U 1 I1
S1
U1
I1
AC 10 lg
10 lg 20 lg
20 lg дБ
U2I2
S2
U2
I2
Величина АС показывает в логарифмическом масштабе, во сколько раз
уменьшилась мощность на выходе четырехполюсника по сравнению с
мощностью на его входе при передаче энергии через четырехполюсник
в согласованном режиме.
Полоса частот, в которой ослабление мало, называется полосой
пропускания (ПП)
Полоса частот, в которой ослабление велико, называется полосой
задерживания (ПЗ)
Идеальный
фильтр:
K ( j ) k const ; K ( j ) 1; AC 0 в ПП
K ( j ) 0; AC
в ПЗ
Граничные частоты полосы пропускания называются частотами среза.

4.

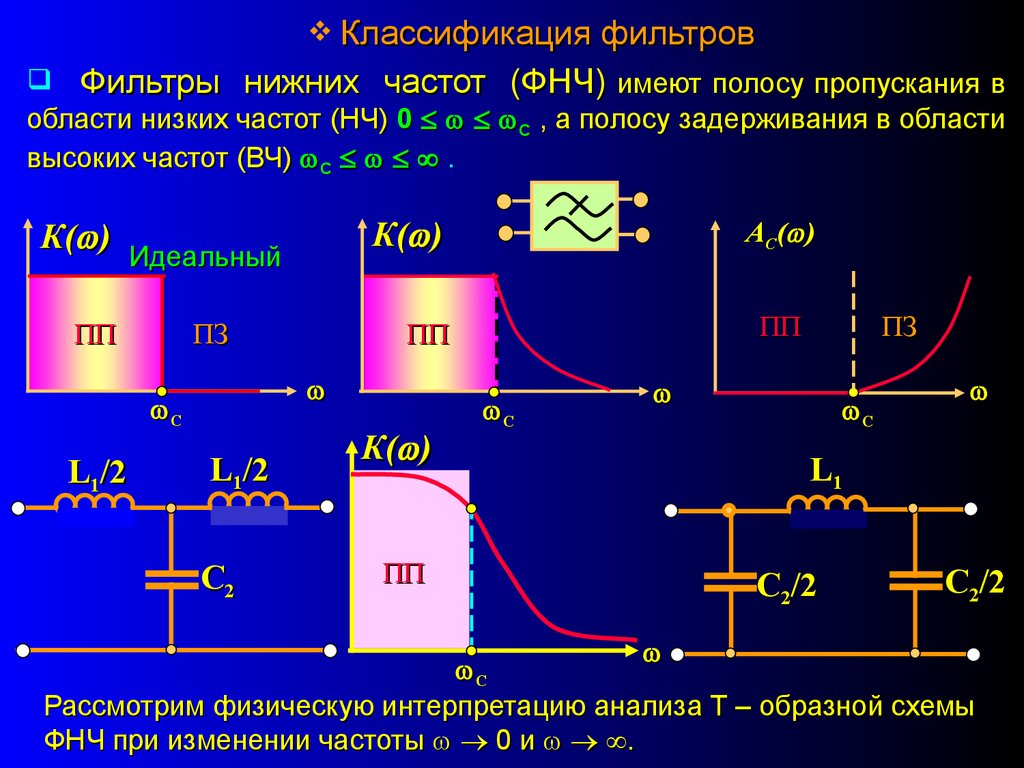
Классификация фильтров
Фильтры нижних частот (ФНЧ) имеют полосу пропускания в
области низких частот (НЧ) 0 С , а полосу задерживания в области
высоких частот (ВЧ) С .
К( )
Идеальный
ПП
ПЗ
L1/2
C2
А С ( )
ПП
ПП
С
L1/2
К( )
К( )
ПП
С
ПЗ
С
L1
C2/2
C2/2
С
Рассмотрим физическую интерпретацию анализа Т – образной схемы
ФНЧ при изменении частоты 0 и .

5.

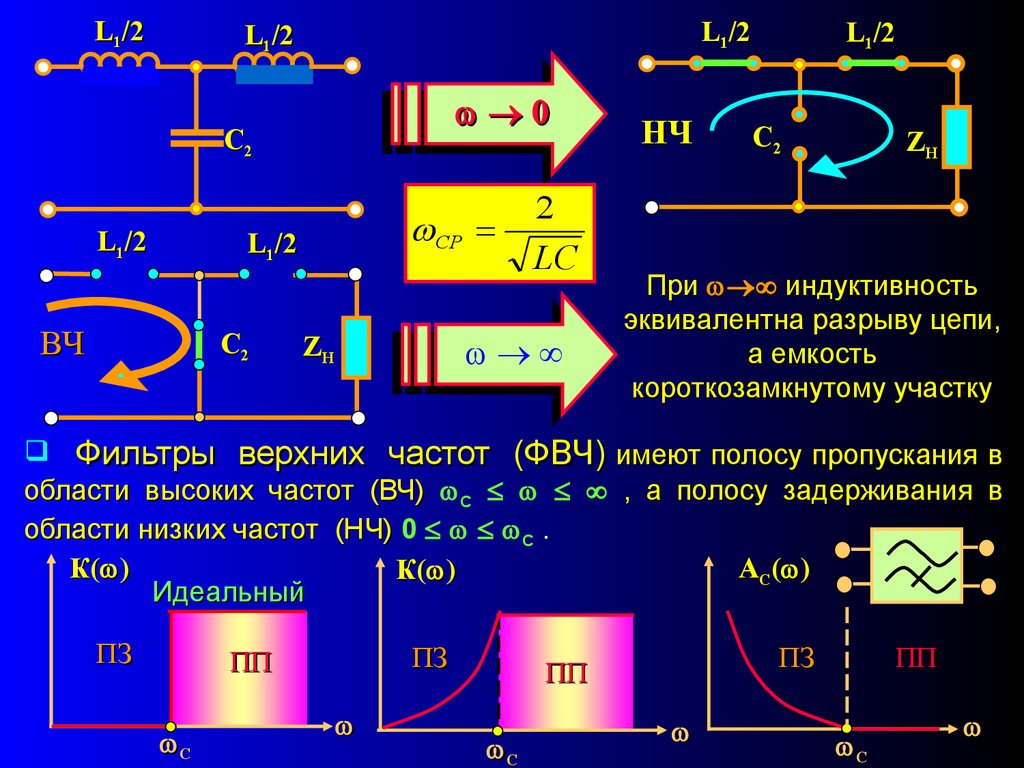
L1/2
L1/2
L1/2
C2
L1/2
СР
L1/2
ВЧ
C2
2
LC
ZН
НЧ
L1/2
C2
ZН
При индуктивность
эквивалентна разрыву цепи,
а емкость
короткозамкнутому участку
Фильтры верхних частот (ФВЧ) имеют полосу пропускания в
области высоких частот (ВЧ) С , а полосу задерживания в
области низких частот (НЧ) 0 С .
К( )
А С( )
К( )
Идеальный
ПЗ
ПЗ
ПП
С
ПЗ
ПП
С
ПП
С

6.

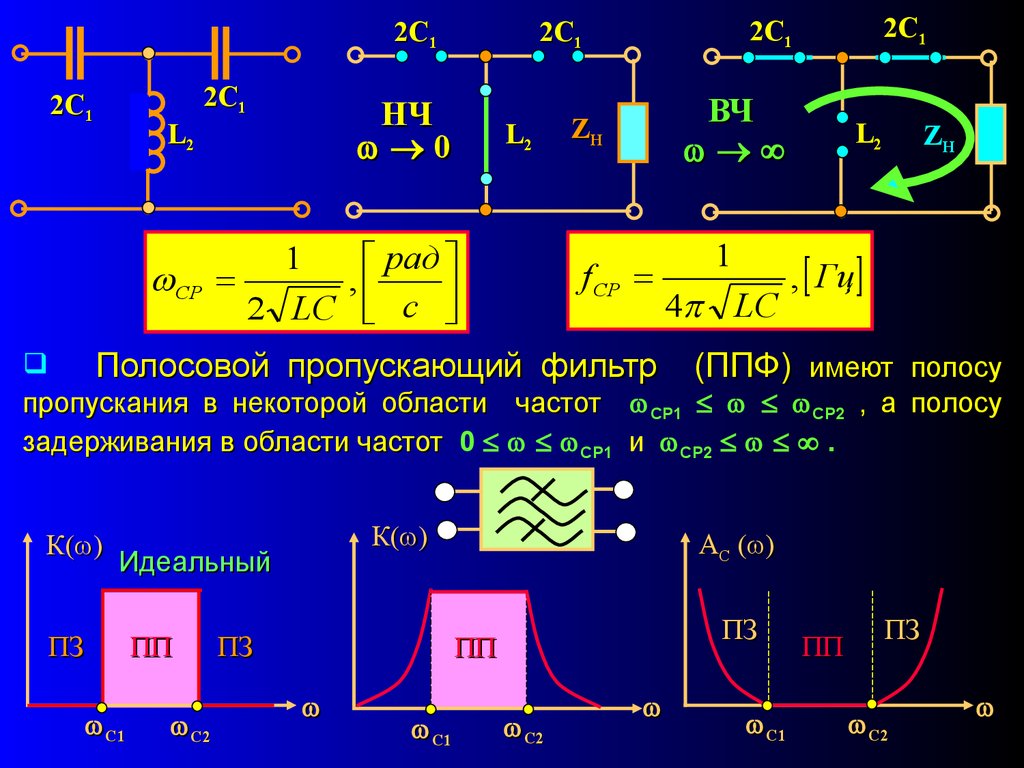
2 C1
2C1
2 C1
НЧ
0
L2
СР
1
2 LC
L2
рад
,
с
2 C1
2 C1
2 C1
ВЧ
ZН
f СР
1
4 LC
L2
ZН
, Гц
Полосовой пропускающий фильтр (ППФ) имеют полосу
пропускания в некоторой области частот СР1 СР2 , а полосу
задерживания в области частот 0 СР1 и СР2 .
К( )
К( )
Идеальный
ПЗ
ПП
С1
С2
ПЗ
АС ( )
ПЗ
ПП
С1
С2
С1
ПП
ПЗ
С2

7.

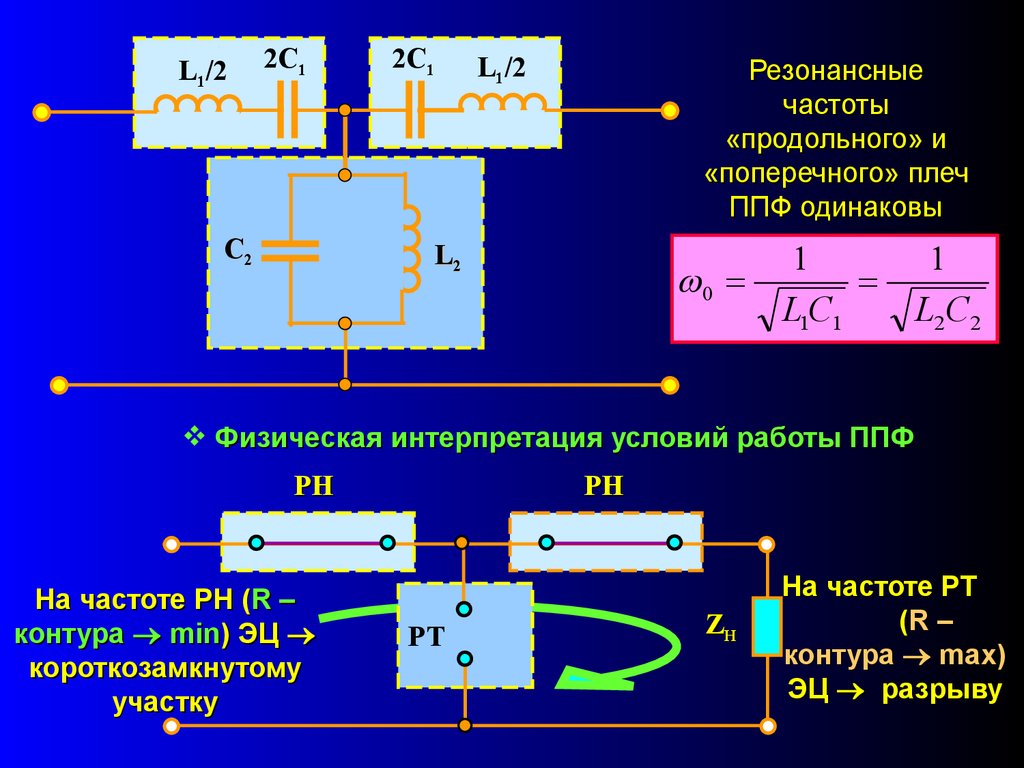
L1/2
2C1
C2
2C1
L1/2
Резонансные
частоты
«продольного» и
«поперечного» плеч
ППФ одинаковы
L2
0
1
L1C1
1
L2C2
Физическая интерпретация условий работы ППФ
РН
На частоте РН (R –
контура min) ЭЦ
короткозамкнутому
участку
РН
РТ
ZH
На частоте РТ
(R –
контура mах)
ЭЦ разрыву

8.

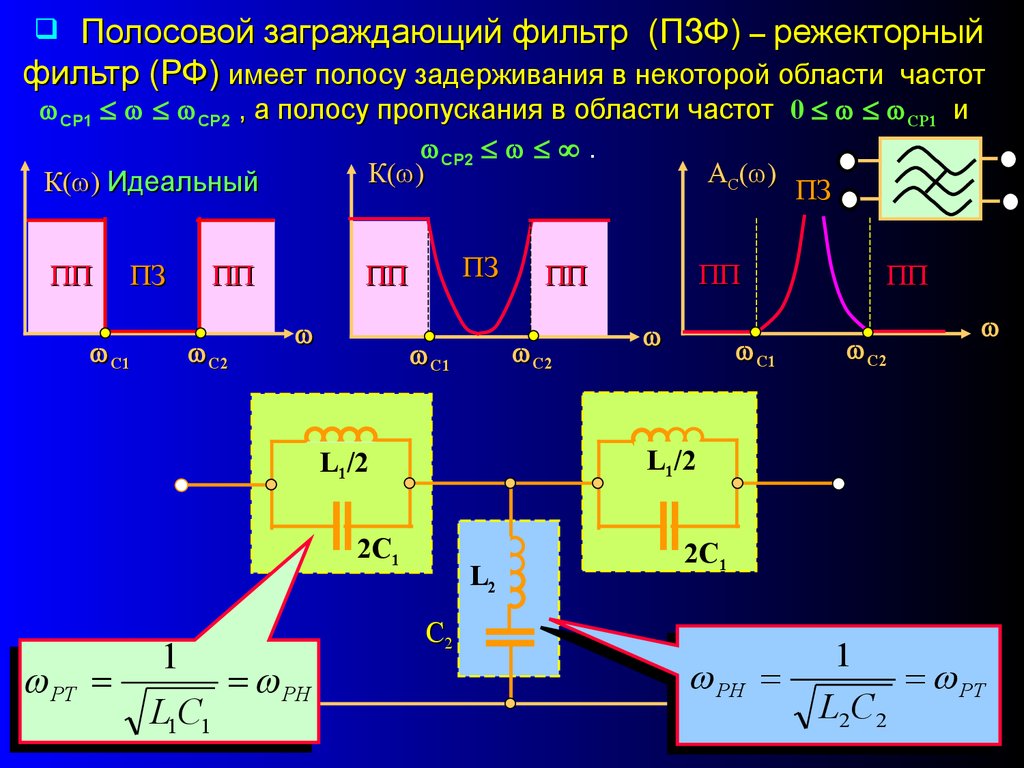
Полосовой заграждающий фильтр (ПЗФ) – режекторный
фильтр (РФ) имеет полосу задерживания в некоторой области частот
СР1 СР2 , а полосу пропускания в области частот 0 СР1 и
СР2 .
К( )
АС( )
К( ) Идеальный
ПЗ
ПП
ПЗ
С1
ПП
С2
ПЗ
ПП
С2
С1
2С1
РТ
С1
ПП
С2
L1/2
L1/2
1
РН
L1C1
ПП
ПП
L2
С2
2С1
РН
1
РТ
L2C2

9.

Требования к электрическим характеристикам фильтров
Избирательность фильтра (степень разграничения полос пропускания и
заграждения) определяется крутизной характеристики рабочего ослабления
UГ
ZH
AP 20 lg
10 lg
, дБ
2U 2
ZГ
Чем больше крутизна этой характеристики и чем сильнее ослабление в
полосе пропускания, тем лучше избирательность фильтра и,
следовательно, меньше уровень помех от подавляемых колебаний.
Требования к электрическим фильтрам задаются в виде
допустимых пределов изменения этих характеристик.
Так рабочее ослабление в полосе пропускания не должно превышать
некоторого максимального допустимого значения AР МАХ, а в полосе
задерживания не должно быть ниже некоторого
минимально
допустимого значения AР МIN
МIN.
Требования к
квадрату АЧХ
2
К ( j )
е 2 АР max , при 0 П
е 2 АР min , при З

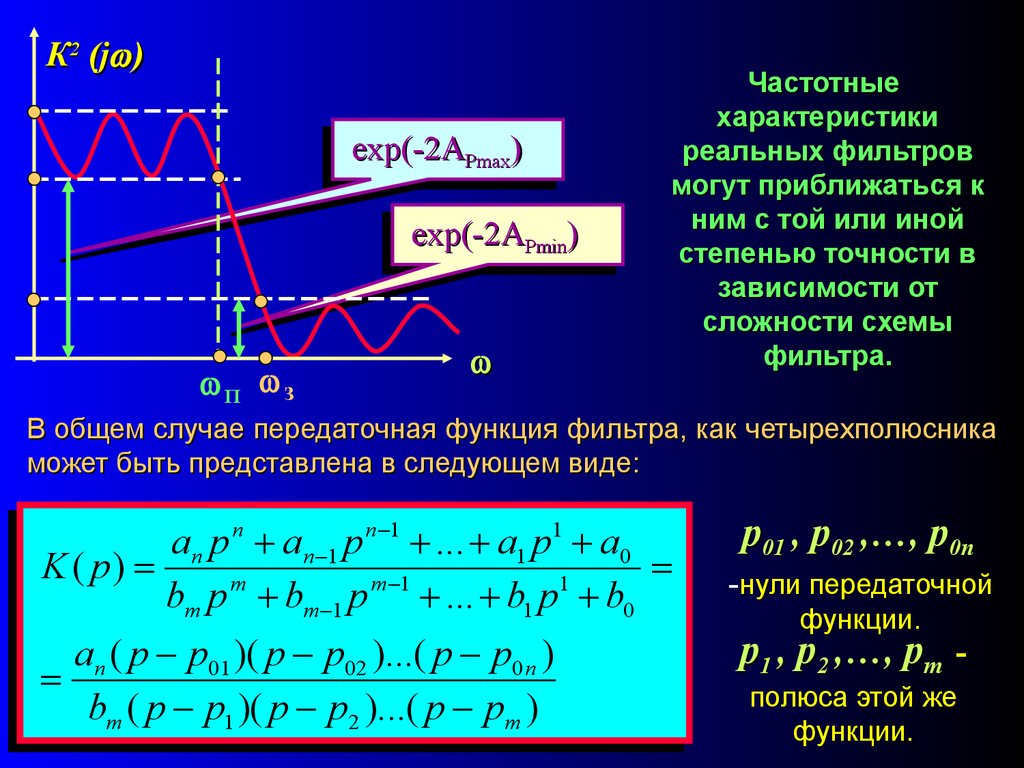
10.

К 2 (j )
exp(-2APmax)
exp(-2APmin)
П
З
Частотные
характеристики
реальных фильтров
могут приближаться к
ним с той или иной
степенью точности в
зависимости от
сложности схемы
фильтра.
В общем случае передаточная функция фильтра, как четырехполюсника
может быть представлена в следующем виде:
an p n an 1 p n 1 ... a1 p1 a0
K ( p)
m
m 1
1
bm p bm 1 p ... b1 p b0
an ( p p01 )( p p02 )...( p p0 n )
bm ( p p1 )( p p2 )...( p pm )
p01 , р02 ,…, р0n
-нули передаточной
функции.
p1 , р2 ,…, рm полюса этой же
функции.

11.

2. Достаточное условие работы классического фильтра в полосе
пропускания
1. Если у симметричного реактивного четырехполюсника в согласованном
установившемся
синусоидальном
режиме
сопротивление
нагрузки
положительно, то такой фильтр работает в полосе пропускания.
2
2
U
U
RC I C2 1 RC I 22 2 при Z H Z ВХ Z С RC 0
RC
RC
2. Если сопротивления симметричного четырехполюсника (фильтра)
ZXX
ZКЗ
и
«разнореактивны» (т.е. одно имеет чисто индуктивный характер, а
второе чисто емкостной), то такой фильтр работает в полосе пропускания.
Для LC – фильтра, с учетом условия 1, можно записать
Z C Z XX ( j ) Z КЗ ( j )
jX XX ( ) jX КЗ ( )
X XX ( ) X КЗ ( ) RC 0
Следовательно, для того чтобы подкоренное выражение было
положительным, значения ХХХ и ХКЗ должны быть разными по знаку.

12.

3. Фильтры нижних частот типа «k» и типа «m»
Классический реактивный фильтр называется фильтром типа k, если
произведение сопротивлений его продольного Z1(j ) и поперечного
Z2(j ) плеч на любой частоте равно постоянному положительному числу,
обозначаемому как k2.
Z1/2
Z1/2
Z2
Z1
ZH
0Т 0,25Z Z1Z 2
2
1
L1/2
ZВХ = ZC
0Т
Z1 ( j ) Z 2 ( j ) k
2Z2
2
Формулы для расчета
характеристических
сопротивлений
0 П
L
2 LC
(1
)
C
4
ZH
Z1 Z 2
1 Z1 / 4 Z 2
L1
L1/2
C2
2Z2
ZH = ZC
ZВХ = ZC
C2/2
C2/2
ZH = ZC
2
L
4
(
)
0 CР
0Т 0 П 0 П
2
C 4 LC
LC

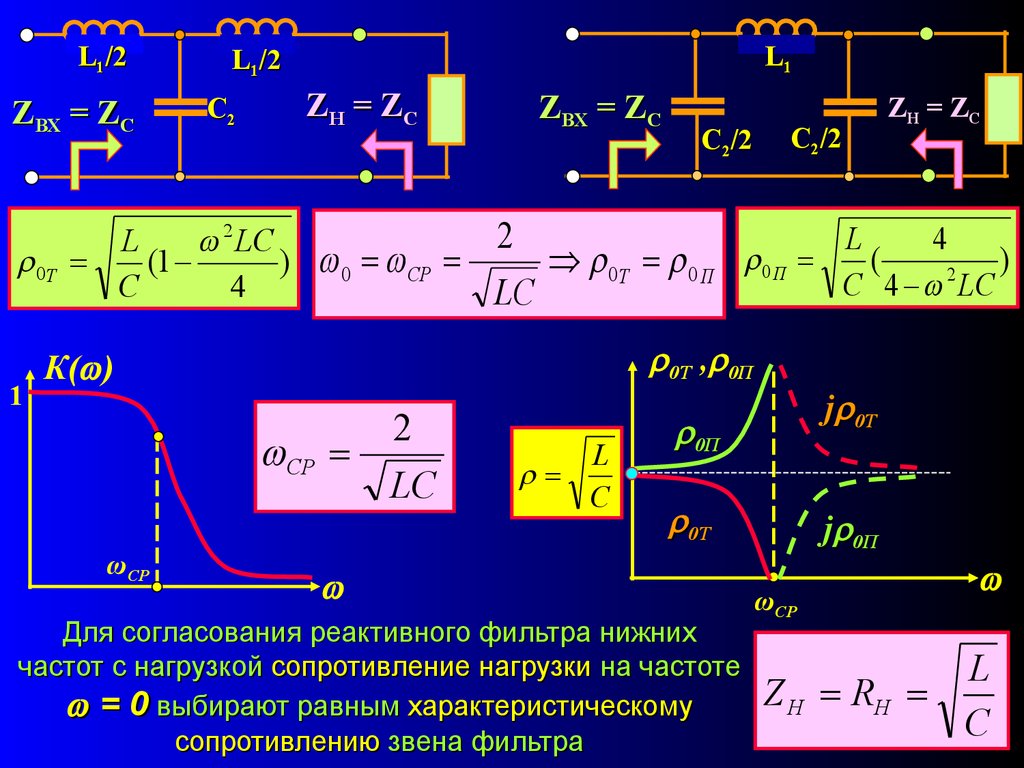
13.

L1/2
ZВХ = ZC
0Т
1
L1
L1/2
ZH = ZC
C2
L
2 LC
(1
)
C
4
ZВХ = ZC
C2/2
2
L
4
)
0 CР
0Т 0 П 0 П (
2
C 4 LC
LC
0Т , 0П
К( )
СР
ωСР
C2/2
ZH = ZC
2
LC
L
C
j 0Т
0П
0Т
Для согласования реактивного фильтра нижних
частот с нагрузкой сопротивление нагрузки на частоте
= 0 выбирают равным характеристическому
сопротивлению звена фильтра
j 0П
ωСР
L
Z H RH
C

14.

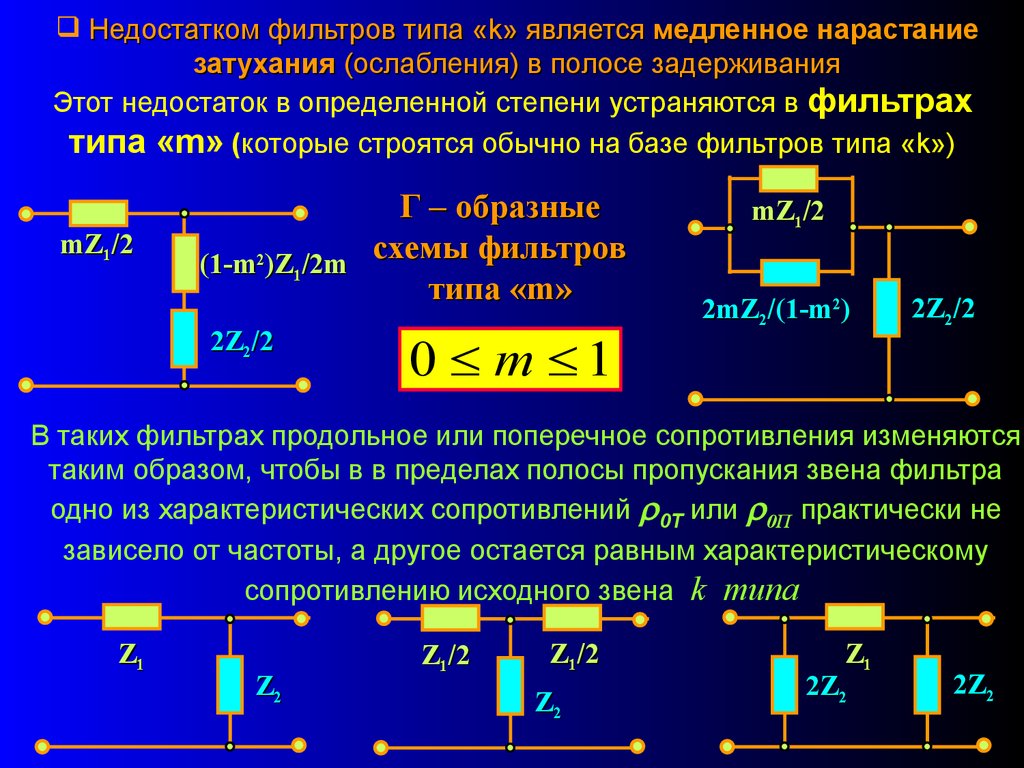
Недостатком фильтров типа «k» является медленное нарастание
затухания (ослабления) в полосе задерживания
Этот недостаток в определенной степени устраняются в фильтрах
типа «m» (которые строятся обычно на базе фильтров типа «k»)
mZ1/2
Г – образные
схемы фильтров
(1-m2)Z1/2m
типа «m»
2Z2/2
0 m 1
mZ1/2
2mZ2/(1-m2)
2Z2/2
В таких фильтрах продольное или поперечное сопротивления изменяются
таким образом, чтобы в в пределах полосы пропускания звена фильтра
одно из характеристических сопротивлений 0Т или 0П практически не
зависело от частоты, а другое остается равным характеристическому
сопротивлению исходного звена k типа
Z1
Z2
Z1/2
Z1/2
Z2
Z1
2Z2
2Z2

15.

Методика определения полосы пропускания
классического фильтра
1. Найти операторные сопротивления ZXX(p) и ZКЗ (p) , а
затем их нули р0k и полюса pk .
2. Размечают р0k и рk на мнимой оси и на каждом
частотном интервале между ними определяют характер
реакции («реактивности») фильтра отдельно для ZXX(p)
и ZКЗ (p) ; зоны, где характер реакции ZXX и ZКЗ различен,
определяют полосу пропускания.
L1/2
L1/2
ZХХ = ?
ZКЗ = ?
C2
ZH

16.

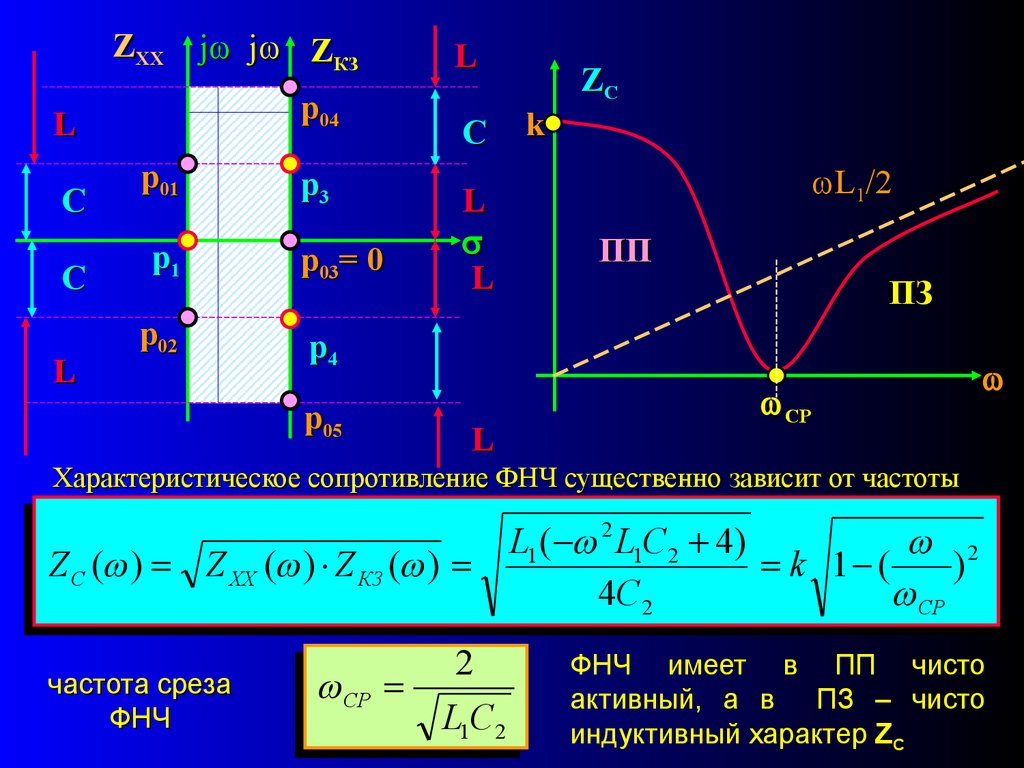
L1/2
Определим сопротивление ХХ
pL1
1
p 2 L1C2 2
Z XX ( p )
2
pC2
2 pC2
ZХХ
L1/2
C2
нули р01, 02 j 2 ( L1C2 ) , полюса р1 0, р2
Определим сопротивление КЗ
L1/2
L1/2
ZКЗ
C2
КЗ
pL1
2 1
Z КЗ ( p )
( рС2
)
2
pL1
pL1 ( p 2 L1C2 4)
2( p 2 L1C2 2)
нули р03 0, p04,05 2 j L1C1 ,
полюса р3, 4 j 2 ( L1C2 ) , р5

17.

ZXX
j j ZКЗ
р04
L
C
C
L
р01
р1
р02
р3
р03= 0
L
C
L
L
ZC
k
L1/2
ПП
ПЗ
р4
р05
L
СР
Характеристическое сопротивление ФНЧ существенно зависит от частоты
Z C ( ) Z XX ( ) Z КЗ ( )
частота среза
ФНЧ
СР
2
L1C2
L1 ( 2 L1C2 4)
2
k 1 (
)
4C2
CP
ФНЧ имеет в ПП чисто
активный, а в ПЗ – чисто
индуктивный характер ZC

18.

4. Полиномиальные фильтры.
Электрические фильтры с передаточной функцией вида
K ( p)
1
bn p n bn 1 p n 1 ... b1 p b0
принято называть полиномиальными
Фильтры, у которых на дополнительной резонансной частоте в полосе
задерживания вблизи частоты среза СР АЧХ «проваливается» до
нуля, благодаря чему она «лучше приближается» к идеальной
принято относить к фильтрам типа m.
L1/2
L1/2
2С1
2С1
С2

19.

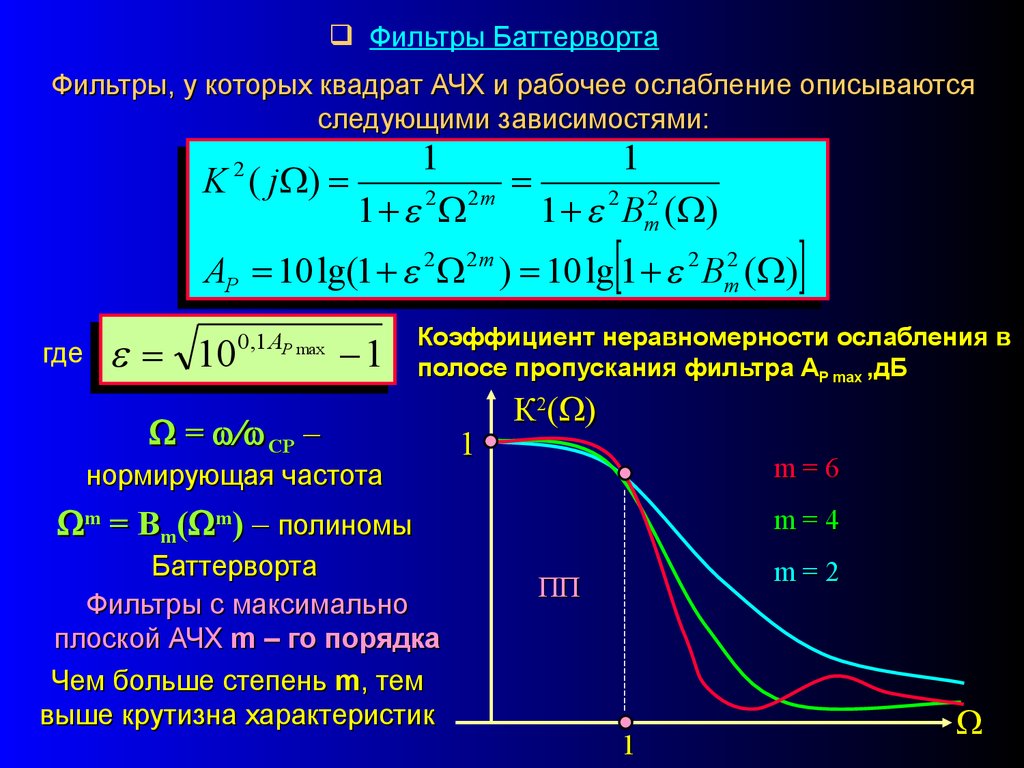
Фильтры Баттерворта
Фильтры, у которых квадрат АЧХ и рабочее ослабление описываются
следующими зависимостями:
1
1
K ( j )
2 2m
1
1 2 Bm2 ( )
2
AP 10 lg(1 2 2 m ) 10 lg 1 2 Bm2 ( )
где
10
0 ,1 АР max
1
Коэффициент неравномерности ослабления в
полосе пропускания фильтра АР max ,дБ
= СР –
нормирующая частота
1
К2( )
m=6
m = Bm( m) – полиномы
Баттерворта
Фильтры с максимально
плоской АЧХ m – го порядка
Чем больше степень m, тем
выше крутизна характеристик
m=4
m=2
ПП
1

20.

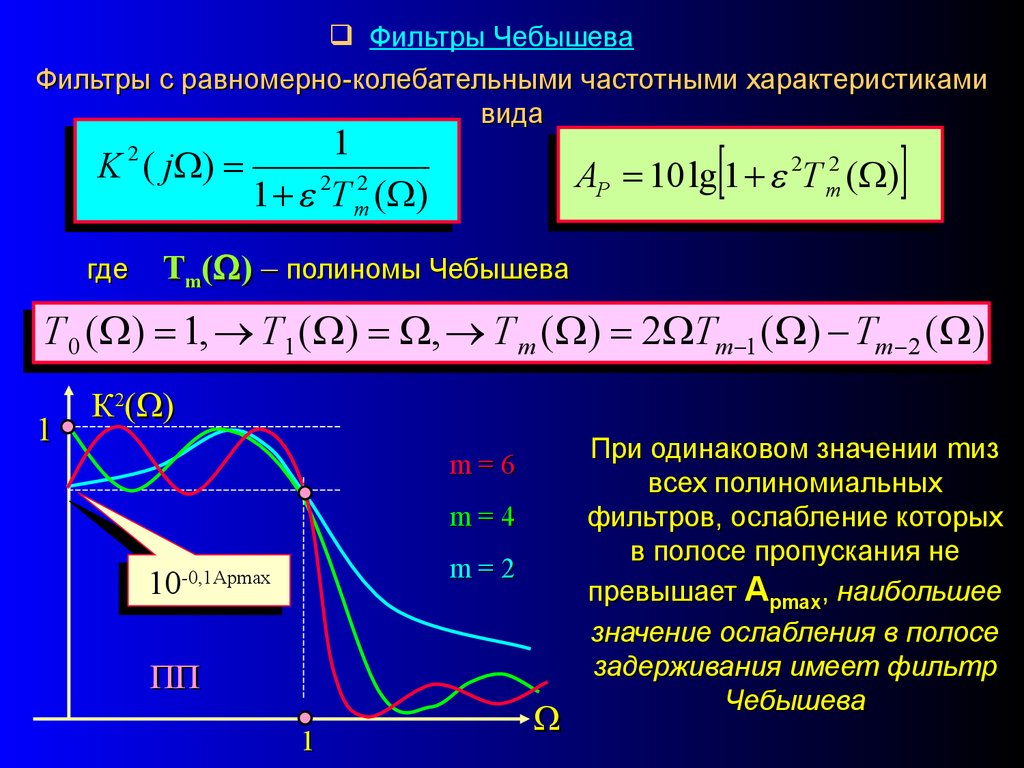
Фильтры Чебышева
Фильтры с равномерно-колебательными частотными характеристиками
вида
1
K ( j )
1 2Т m2 ( )
2
где
AP 10 lg 1 2Т m2 ( )
Тm( ) – полиномы Чебышева
Т 0 ( ) 1, Т1 ( ) , Т m ( ) 2 Tm 1 ( ) Tm 2 ( )
1
К2( )
m=6
m=4
m=2
-0,1Арmax
10-0,1Арmax
10
ПП
1
При одинаковом значении mиз
всех полиномиальных
фильтров, ослабление которых
в полосе пропускания не
превышает Арmax, наибольшее
значение ослабления в полосе
задерживания имеет фильтр
Чебышева

21.

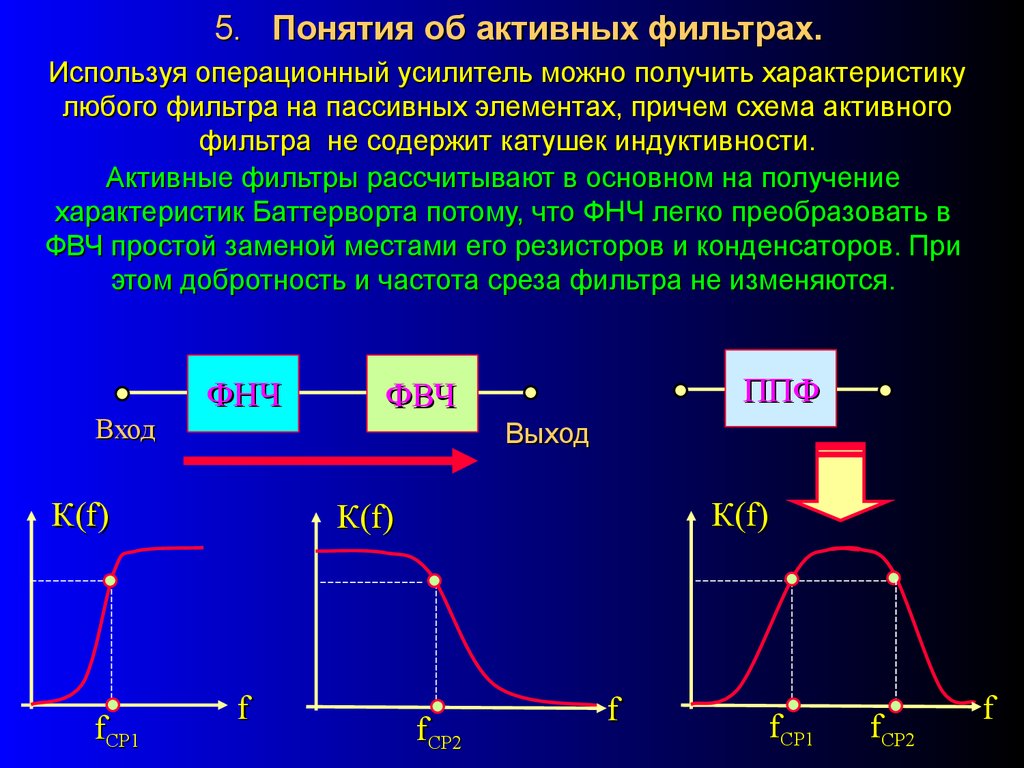
5. Понятия об активных фильтрах.
Используя операционный усилитель можно получить характеристику
любого фильтра на пассивных элементах, причем схема активного
фильтра не содержит катушек индуктивности.
Активные фильтры рассчитывают в основном на получение
характеристик Баттерворта потому, что ФНЧ легко преобразовать в
ФВЧ простой заменой местами его резисторов и конденсаторов. При
этом добротность и частота среза фильтра не изменяются.
Вход
ФНЧ
Выход
К(f)
fСР1
ППФ
ФВЧ
К(f)
К(f)
f
fСР2
f
fСР1
fСР2
f

22.

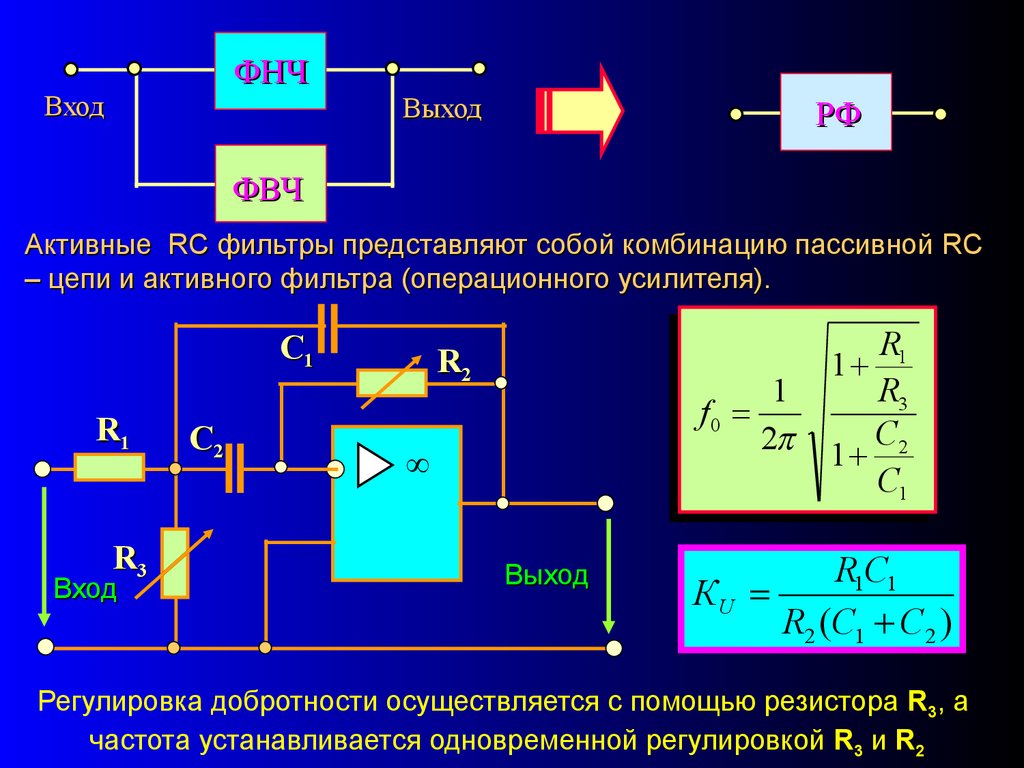
ФНЧ
Вход
Выход
РФ
ФВЧ
Активные RC фильтры представляют собой комбинацию пассивной RC
– цепи и активного фильтра (операционного усилителя).
C1
R1
R3
Вход
C2
R2
1
f0
2
Выход
R1
1
R3
C
1 2
C1
R1C1
КU
R2 (C1 C2 )
Регулировка добротности осуществляется с помощью резистора R3, а
частота устанавливается одновременной регулировкой R3 и R2

23.

Задание на самостоятельную работу
Литература:
Литература
1. Зевеке Г.В., Ионкин А.В., Нетушил А.В.,Страков С.В. Основы теории
цепей: Учебник для вузов, - М.: Энергоатомиздат, 1999 г, с. 169 –187.
2. Бакалов В.П., Игнатов А.Н., Крук Б.И. Основы теории электрических
цепей и электроники: Учебник для вузов, - М.: Радио и связь, 1999 г, с. 208 –
227.
3. Касаткин А.С., Немцов М.В. Электротехника: Учебник для вузов, - М.:
Высшая школа, 2003 г, с. 128 –132.
4. Фрикс В.В. Основы теории цепей: Учебное пособие для межвузовского
использования вузов, - М.: Радио Софт, 2002 г, с. 250 –259.