Похожие презентации:
Дифференциальное исчисление функций нескольких переменных
1. Дифференциальное исчисление функций нескольких переменных
2. Примеры функций нескольких переменных
S(a, b)=a·b – площадь прямоугольника состоронами a и b.
m
T 2
k
– период колебаний груза массы m
на пружине с жесткостью k.
P
R
a b
– уровень рентабельности зависит от
прибыли Р на реализованную продукцию,
величины основных а и b оборотных фондов.
3. Декартово произведение
E1 E2 ... En( x1 , x2 ,..., xn ) | xi Ei
i Ei R R
n
4. Функция п действительных переменных
Отображение f: Х →R, где X R nназывается действительной функцией п
действительных переменных (аргументов).
Соответствие f, которое для каждой пары
действительных чисел (х; у) из множества
2
D R определяет один и только один
элемент z из множества Z, называется
однозначной функцией двух переменных.
5. Функции
z=f(x; y)f: D →Z
y=f(x1; x2;…; xn)
y f (x )
f: Х →R
Область определения
(существования) функции
6. Окрестность точки
δ-окрестностью точки М0 (х0; у0) называетсямножество всех точек М(х; у) плоскости хОу,
координаты удовлетворяют неравенству
( x x0 ) ( y y0 )
2
М0 δ
2
(M ; M 0 ) ( x x0 )2 ( y y0 )2
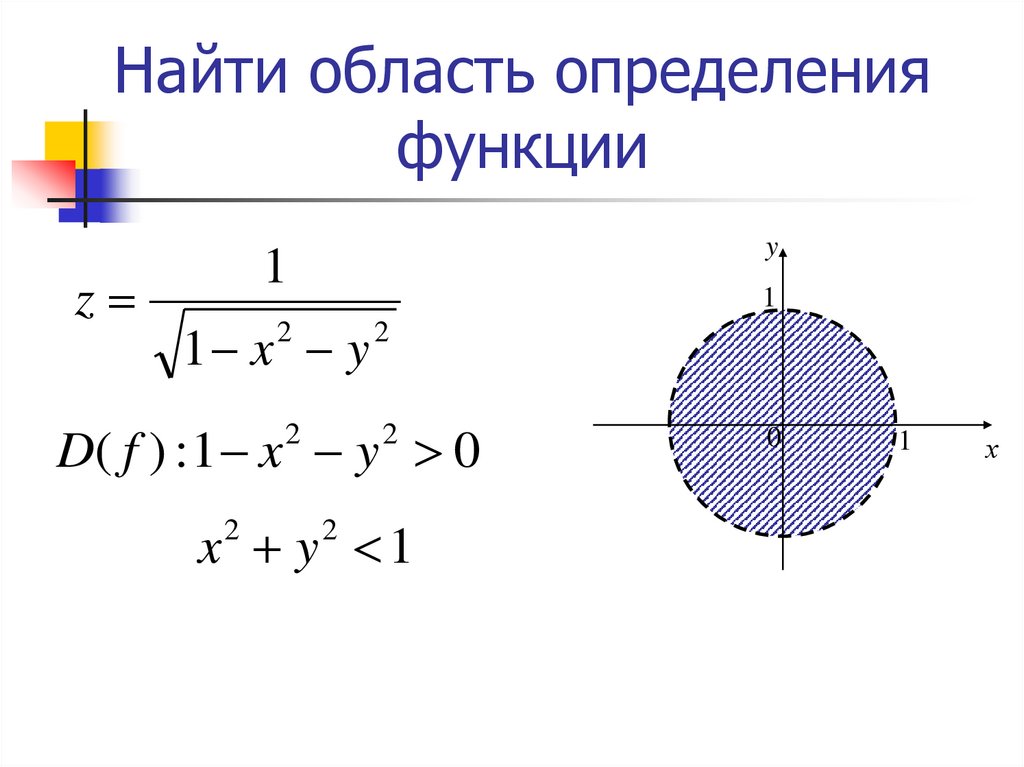
7. Найти область определения функции
zy
1
1
1 x y
2
2
D( f ) : 1 x y 0
2
2
x y 1
2
2
0
1
х
8. График функции f: Х→R
( x1 , x 2 ,..., x n , y ) Rn 1
: y f ( x1 , x 2 ,..., x n )
При п=2 графиком функции является
поверхность в R3.
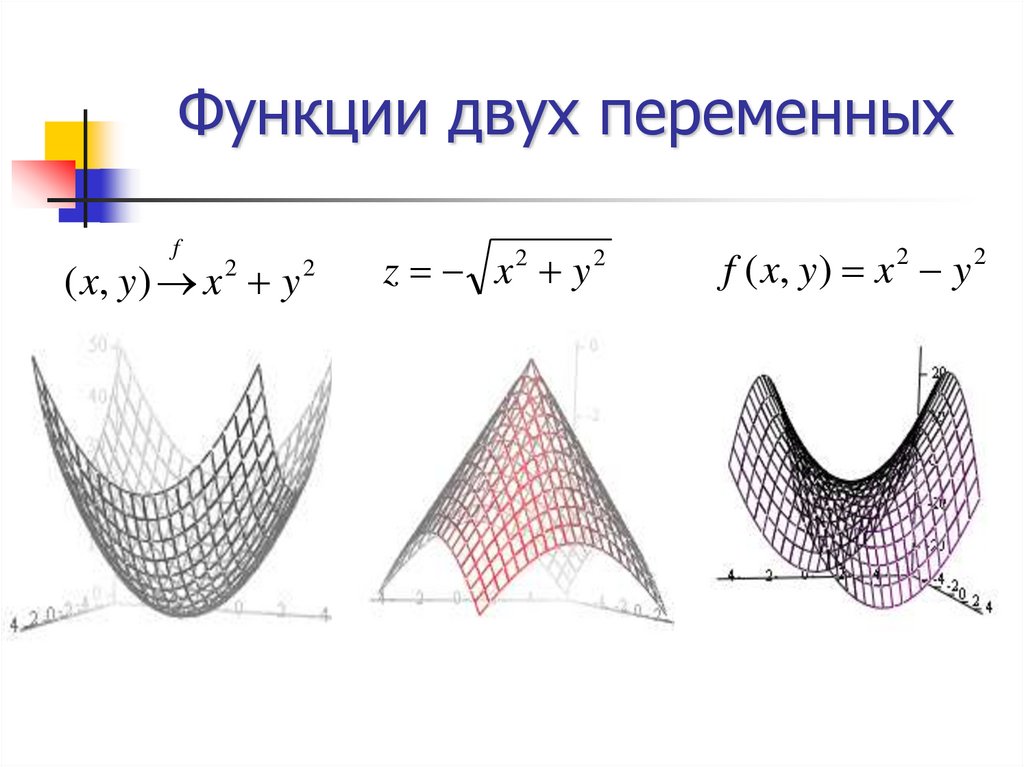
9. Функции двух переменных
f( x, y ) x y
2
f ( x, y) x 2 y 2
z x2 y2
2
F
F
10. Предел функции в точке М0 (х0; у0) (при х→х0 и у→у0)
A lim f ( x; y ) 0 ( ) 0 :M M 0
x x0 , y y0 ( M ; M 0 )
| f ( x; y ) A |
lim f ( x; y) lim f ( x; y)
M M 0
x x0
y y0
11. Непрерывность функции в точке
Функция z = f(x,y) называетсянепрерывной в точке М0 (х0; у0), если
lim f ( x; y) f ( x0 ; y0 )
x x0
y y0
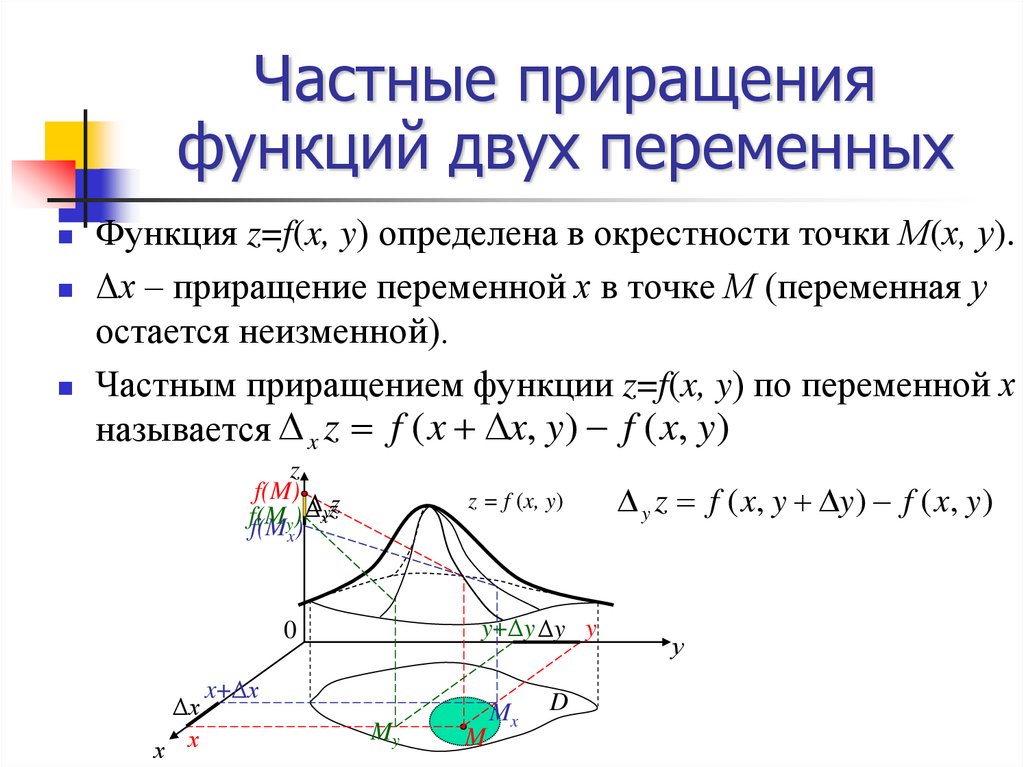
12. Частные приращения функций двух переменных
Функция z=f(x, y) определена в окрестности точки М(х, у).Δх – приращение переменной х в точке М (переменная у
остается неизменной).
Частным приращением функции z=f(x, y) по переменной х
называется x z f ( x x, y) f ( x, y)
z
f(M) Δ z
Δхyz
f(M
)
y
f(Mx)
z = f (x, y)
y+Δy Δy y
0
Δх
х х
x+Δх
My
M
Mx
D
y z f ( x, y y ) f ( x, y )
у
13. Частные производные функции двух переменных
Частной производной функции z=f(x, y) попеременной х называется предел, если он
существует, отношения частного
приращения функции по переменной х к
приращению этой переменной, когда
последнее стремится к 0.
xz
z
f ( x x, y ) f ( x, y )
lim
lim
x x 0 x x 0
x
14. Частные производные функции двух переменных
zz
f ( x x, y ) f ( x, y )
lim x lim
x x 0 x x 0
x
y f
z
f ( x, y y) f ( x, y)
lim
lim
y y 0 y y 0
y
Частные
производные
функции z по
переменным х и у.
Обозначения частной производной функции z=f(x, y)
f
по переменной х: f x/ ( x, y )
z x
x
вычисленной в точке М(х0, у0)
f x ( x0 , y0 )
z
x
x x0
y y0
15. Геометрический смысл частных производных
zP( x0 , y0 , f ( x0 , y0 ))
х=х0
z = f (x, y)
z = f (x0, y)
z = f (x, y0)
Р
0
х0
х
α
у0
f x/ ( x0 , y0 ) tg
f y/ ( x0 , y0 ) tg
у
β
M0
Частная производная f /x(x0, y0) – угловой
коэффициент касательной к линии
пересечения поверхности z = f(x,y) и
плоскости у=у0 в соответствующей точке.
16.
Полное приращениефункций двух переменных
z
z = f (x, y)
0
х
x+Δх Δх
х
y+Δy
Δу у
у
M
z f ( x x, y y ) f ( x, y )
17. Дифференцируемость функции
Функция z=f(x; y) называетсядифференцируемой в точке М, если
полное приращение этой функции
z f ( x x, y y ) f ( x, y )
можно представить в виде
z A x B y о( )
о( )
2
2 lim
0
x y x 0
y 0
18. Полный дифференциал функции
Полным дифференциаломдифференцируемой функции z=f(x; y) в точке
М называется главная часть её приращения,
линейная относительно Δх и Δу, т.е.
z A x B y о( )
dz A x B y
dz A dx B dy
19. Необходимое условие дифференцируемости функции
Если функция z=f(x; y) дифференцируемав точке М(х; у), то она непрерывна в этой
точке и имеет в ней частные
z
z
производные, причем
A
x
z
z
dz dx dy
x
y
; B
y
20. Достаточное условие дифференцируемости функции
Если функция z=f(x; y) в точке М(х; у)имеет непрерывные частные
производные, то она дифференцируема в
этой точке.
21. Частные производные высших порядков
z z,
x y
z = f (x, y)
частные производные первого порядка
(непрерывные и имеют частные производные)
z z
2
x x x
2
z z
2
y y y
2
z
z z
z
2
x2
x
y x x y
2
2
частные
производные
второго
порядка
z z
x y y x
2
Смешанные
22. Частные производные высших порядков
zz
z
xy
2
y
x y
y x y
3
f
2
(n)
xi 1 xi 2 ... xi n
f
частная
( 3) производная
z xy 2
третьего
порядка
( n 1)
xi 1 xi 2 ... xi n 1
xi n
23. Теорема Шварца
zz
x y y x
2
2
z
z
z
2
2
y x y y x x y
3
3
3
Если функция от п переменных определена в
открытой п-мерной области, в которой
существуют частные производные до (k–1)го порядка включительно и смешанные
производные k-го порядка включительно и
все эти производные непрерывны, то
смешанные производные k-го порядка,
отличающиеся
лишь
порядком
дифференцирования, равны между собой.
24. Дифференциалы высших порядков
z = f (x, y)z
z
полный дифференциал
dz dх dу первого порядка
х
у
d z d (dz )
2
дифференциал
второго порядка
z 2
z
z 2
d z 2 dх 2
dxdу 2 dу
х
x у
у
2
2
2
2
25. Точки экстремума
Функция z=f(x, y) определена в области DТочка М0(х0, у0) области D называется точкой локального максимума
(минимума) если существует В(М0, δ), что для всех точек М(х, у) из
В(М0, δ)∩D выполняется неравенство f(x0, y0) ≥ f(x, y) ( f(x0, y0) ≤ f(x, y)).
Точки максимума и минимума (Δz – знакопостоянно) функции
называются точками экстремума, а значения функции в этих точках –
экстремальными.
z
z
z = f (x, y)
z = f (x, y)
у
М0
х
у
М0
М
х
26. Необходимое условие существования экстремума
Если функция z=f(x, y) определена и дифференцируема вВ(М0, δ) и имеет в точке М0(х0, у0) экстремум, то в этой
точке частные производные первого порядка равны нулю:
f ( M 0 )
f ( M 0 )
0
0
x
y
z
Эта система эквивалентна
уравнению df(x, y)=0.
z = f (x, y)
у
М0
х
М
27.
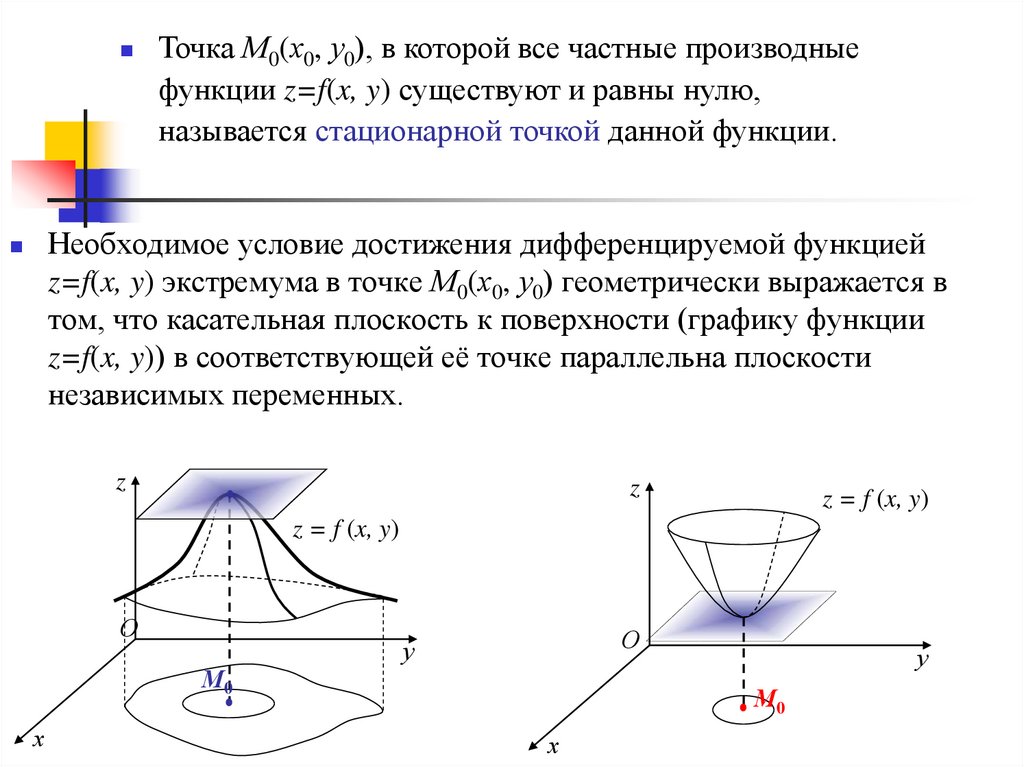
Точка М0(х0, у0), в которой все частные производныефункции z=f(x, y) существуют и равны нулю,
называется стационарной точкой данной функции.
Необходимое условие достижения дифференцируемой функцией
z=f(x, y) экстремума в точке М0(х0, у0) геометрически выражается в
том, что касательная плоскость к поверхности (графику функции
z=f(x, y)) в соответствующей её точке параллельна плоскости
независимых переменных.
z
z
z = f (x, y)
z = f (x, y)
О
М0
х
О
у
у
М0
х
28. Замечание.
Функция z=f(x, y) может иметь экстремум и в таких точках, в которыхпо крайней мере одна из частных производных не существует.
Например, функция z x 2 y 2 в точке О(0, 0) имеет минимум, но в
этой точке частные производные первого порядка не существуют.
f
x
f
y
z
x
x y
2
z x2 y2
2
y
x y
2
у
2
х
Точки, в которых частные производные равны нулю или хотя бы одна
из них не существуют, называются критическими точками.
29. Достаточное условие существования экстремума
Случай функции двух переменныхПусть функция z=f(x, y) определена, непрерывна и непрерывно
дифференцируема до второго порядка включительно в некоторой
окрестности точки М0(х0, у0), причем grad f ( M 0 ) 0. Обозначим
2 f (M 0 )
2 f (M 0 )
2 f (M 0 )
a11 a12
a
a
a
11
22
12
x 2
y 2
x y
a21 a22
Если Δ>0, а11<0, то точка М0(х0, у0) – точка максимума;
Если Δ>0, а11>0, то точка М0(х0, у0) – точка минимума;
Если Δ<0, то точка М0(х0, у0) не является точкой экстремума;
Если Δ=0, то требуются дополнительные исследования.
Точка М0(х0, у0) является точкой экстремума если d2f (M0) знакопостоянен.
30. Замечание.
Стационарная точка функции z=f(x, y) может и не являться точкойэкстремума.
Например, функция z x 2 y 2 в точке О(0, 0) не имеет экстремума,
хотя в этой точке частные производные первого порядка равны нулю.
f
2x
x
2
0
0 2
f
2 y
y
f ( x, y) x 2 y 2
z
у
4 0
х
F
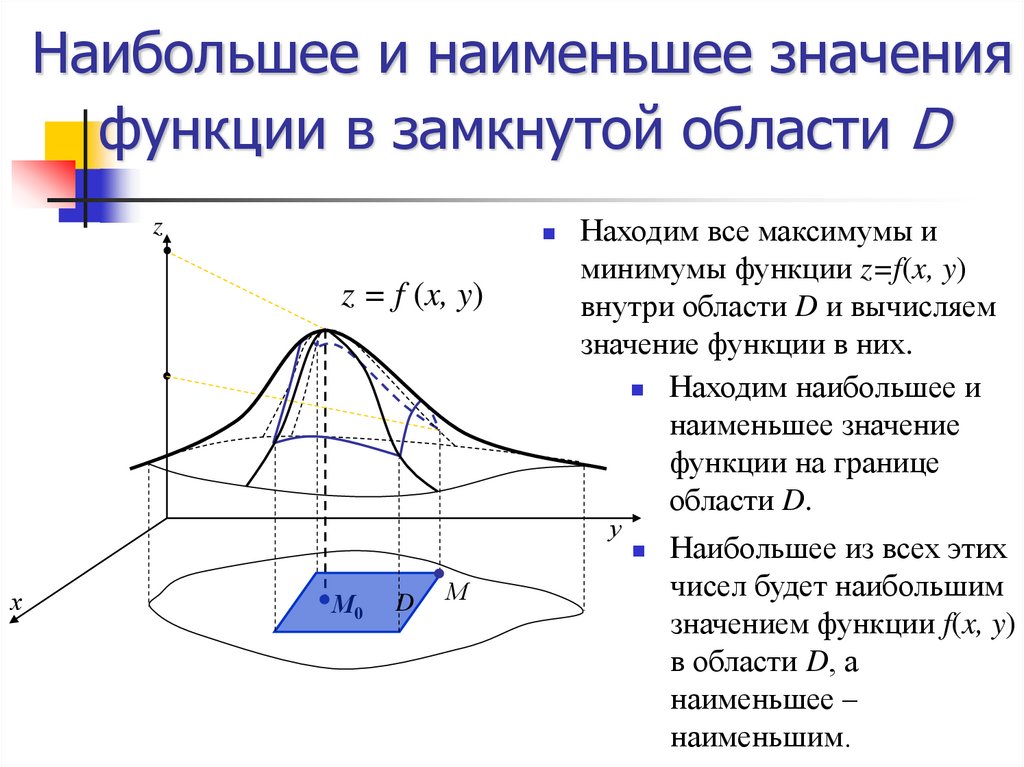
31. Наибольшее и наименьшее значения функции в замкнутой области D
zz = f (x, y)
Находим все максимумы и
минимумы функции z=f(x, y)
внутри области D и вычисляем
значение функции в них.
Находим наибольшее и
наименьшее значение
функции на границе
области D.
у
х
М0
D
М
Наибольшее из всех этих
чисел будет наибольшим
значением функции f(x, y)
в области D, а
наименьшее –
наименьшим.


























 Математика
Математика








