Сращивание асимптотических разложений. Модельные задачи. (Лекция 6)

1. Введение в асимптотические методы. Лекция 6

Сращивание асимптотических
разложения: модельные задачи

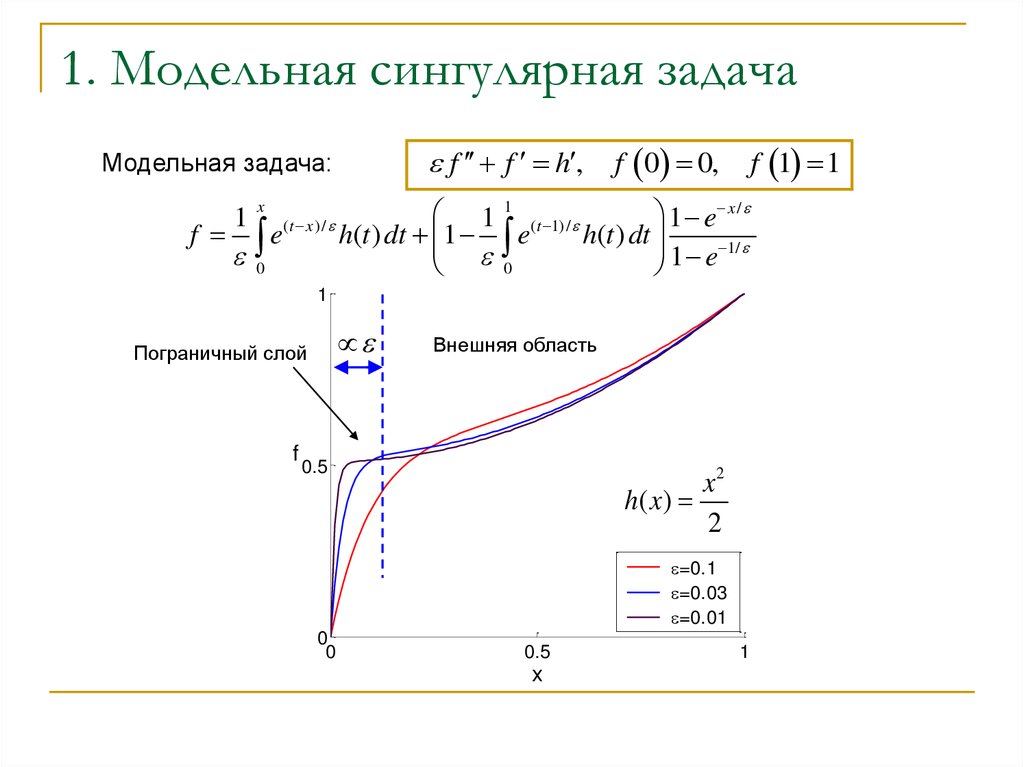
2. 1. Модельная сингулярная задача

f f h ,
Модельная задача:
f
1
x
e
(t x ) /
0
f 0 0,
f 1 1
1 1 (t 1) /
1 e x /
h(t ) dt 1 e
h(t ) dt
1/
1
e
0
1
Пограничный слой
f
Внешняя область
0.5
x2
h( x )
2
=0.1
=0.03
=0.01
0
0
0.5
x
1

3. 2. Внешнее разложение

f f h ,
f 0 0,
f 1 1
f f 0 ( x) f1 ( x) 2 f 2 ( x)
f0 h , f0 0 0, f0 1 1
f1 f0 , f1 0 0, f1 1 0
f2 f1 ,
f 2 0 0,
f 2 1 0
f 0 ( x) h( x) h(1) 1
f1 ( x) h ( x) h (1)
f 2 ( x) h ( x) h (1)
Нельзя удовлетворить обоим граничным условиям.
Значит существуют погранслои, в которых данное
АР неприменимо. Нам известно, что ПС находится
в точке x=0, но не x=1.
То, что внешнее разложение полностью определено,
является спецификой рассматриваемой задачи. В
общем случае оно содержит неопределенные
константы интегрирования.

4. 3. Внутреннее разложение

f 0 0,
f f h ,
x/
f ( x, ) F ( , )
Погранслойная координата:
f 1 1
Нам известно, что ПС находится в
точке x=0, и имеет ширину .
1 d 2 F 1 dF
1 2
h
h
(0)
h
(0)
h (0) 2
2
2
d
d
F F0 ( ) F1 ( ) 2 F2 ( )
d 2 F0 dF0
0, F0 (0) 0
d 2 d
d 2 F1 dF1
h (0), F1 (0) 0
2
d
d
d 2 F2 dF2
h (0), F2 (0) 0
2
d
d
F0 A0 1 e
?
F1 h (0) A1 1 e
F2 h (0) 12 2 A2 1 e

5. 4. Сращивание: правило Ван Дайка

Внешний предел внутреннего разложения равен
внутреннему пределу внешнего разложения
E2( m ) E1( n ) f ( , ) E1( n ) E2( m ) F ( x, )
m n 3
1) подставляем во внешнее разложение x и проводим разложение
полученного выражения по с удержанием трех главных членов
E2(3)
E f ( , ) h( ) h(1) 1 h ( ) h (1)
(3)
1
2
h ( ) h (1)
h(0) h (0) 12 2h (0) 2 h(1) 1 h (0) h (0) h (1) 2 h (0) h (1)
2) подставляем во внутреннее разложение x / и проводим разложение
полученного выражения по с удержанием трех главных членов
E1(3)
E F ( x, ) A 1 e h (0) x A 1 e
h (0) x x A 1 e
x /
(3)
2
0
2
1
2
2
0
1
2
A h (0) x
x/
1
x /
1
2
1
2
h (0) x 2 A1 h (0) x 2 A2

6. 5. Сращивание: правило Ван Дайка

Внешний предел внутреннего разложения равен
внутреннему пределу внешнего разложения
m n 3
3) переходим в первом из этих разложений от переменной к переменной x
E2(3)
E f ( , )
(3)
1
x
h(0) h (0) x 12 h (0) x 2 h(1) 1
h (0) h (0) x h (1) 2 h (0) h (1)
4) сравнивая полученное выражение с
E1(3) E2(3) F ( x, ) A0 h (0) x 12 h (0) x 2 A1 h (0) x 2 A2
находим
A0 h(0) h(1) 1,
A1 h (1) h (0),
A2 h (0) h (1).
E2( m ) E1( n ) f ( , ) E1( n ) E2( m ) F ( x, )

7. 6. Равномерно пригодное разложение

Cn ,m f E1( n ) f E2( m ) F E1( n ) E2( m ) F ( x, )
составное
разложение
внешнее
внутреннее
общая часть
C1,1 f h( x ) h(1) 1 h(0) h(1) 1 1 e x / h(0) h(1) 1
h( x ) h(1) 1 h(0) h(1) 1 e x / .1
=0.1
C22 f C11 f
h ( x) h (1) h (0) h (1) e x /
f 0.5
exact
E0
H0
C00
C11
0
0
0.5
x
1

8. 7. Толщина погранслоя

Толщина ПС
0
0 1
1
1
f xx
0, ?
Погранслойная координата x /
fx
hx
……. баланс……
главный
……….. баланс………....
главный
внешнее
перекрытие
внутреннее
под-внутреннее
Потенциально интересны те перенормировки, которые обеспечивают
баланс 2-х или более членов уравнения
!
Важно, что в области перекрытия внешнего и внутреннего разложения, т. е.
при 0 1внешняя и внутренняя задачи имеют в качестве главного один и
тот же (конвективный) член. Именно это обстоятельство в конечном итоге и
позволяет срастить внешнее и внутреннее разложения.

9. 8. Толщина погранслоя: пример 2

f x f f 0,
x f0 f0 0,
Внешнее АР
Толщина ПС
f (0) 0,
f0 (1) 1
f (1) 1
f0 e
2
x 1
x / 1 2 f / 2 f f 0 1 2 / 2
Внутреннее АР
g0 g0 0, g0 (0) 0 g0 A exp 23 d
0
Сращивание
f 0 (0) g 0 ( )
A e
2
2
exp
d
3
0
2
3

10. 9. Толщина погранслоя: пример 3

Во многих задачах толщина пограничного слоя подсказывается самим
видом внешнего разложения
dy
y y 2 x,
x 1;
y (1) 1
dx
y x 1 e1 x x 2 4 x 5 x 2 2 x e1 x e2(1 x )
главный и следующий члены разложения становятся соизмеримы, а значит,
разложение разваливается при x 1
Пограничный слой в этой задаче лежит на бесконечности, и при его изучении
1
необходимо нормировать пространственную координату на . В отличие от
рассмотренных выше задач, здесь оказывается необходимым перенормировать также и искомую функцию . На этого также указывает полученное
1
1
разложение : при x
оба его члена разложения имеют порядок .
Поэтому подходящей перенормировкой при изучении ПС будет
x , Y y

11. 10. Толщина погранслоя: пример 3

dY
Y Y 2
d
1 1 4
Y Y 2 Y
2
В главном члене
Для выбора знака нужно срастить главные члены внутреннего и внешнего
разложений
верный
E2(1) E1(1) y ( , ) 1 e1 / 1 x
выбор
1 1 4 x 1 1 2 x
x
(1)
(1) 1
E1
E2 Y ( x , )
1
2
2
Составное разложение
1 4 x 1
2x
1 x
C1,1 ( y ) x 1 e1 x
x
e
1
2
1 1 4 x

12. 11. Где пограничный слой?

Помогают узнать:
Численные расчеты
Физические соображения
Если угадано неправильно, то не удастся срастить разложения
Пример 1: 2 ПС на обоих концах интервала
2 f f 1,
f
f (0) 0,
1
f (1) 0
1 e x / e( x 1) /
0
Пример 2: ПС в середине интервала
f 2 xf 2 x,
f
1
f ( 1) 0,
x erf x
1
f (1) 0
-1
0
-1
1

13. 12. Где пограничный слой? Пример 4

y yy y 0,
y (0) A,
0 y 1
y (1) B.
y0 y0 y0 0 y0 0, y0 x const
Главный член внешнего разложения
y0 R ( x ) x B 1
y0 L ( x ) x A
x xd , Y , y x,
Погранслой
Y Y0 ( ) Y1 ( )
Y0
Y0 Y0Y0 0
Y0 ( ) th
1
1
Y0 Y02 2
2
2
2
Y0 ( ) cth
2
k
k
th
cth

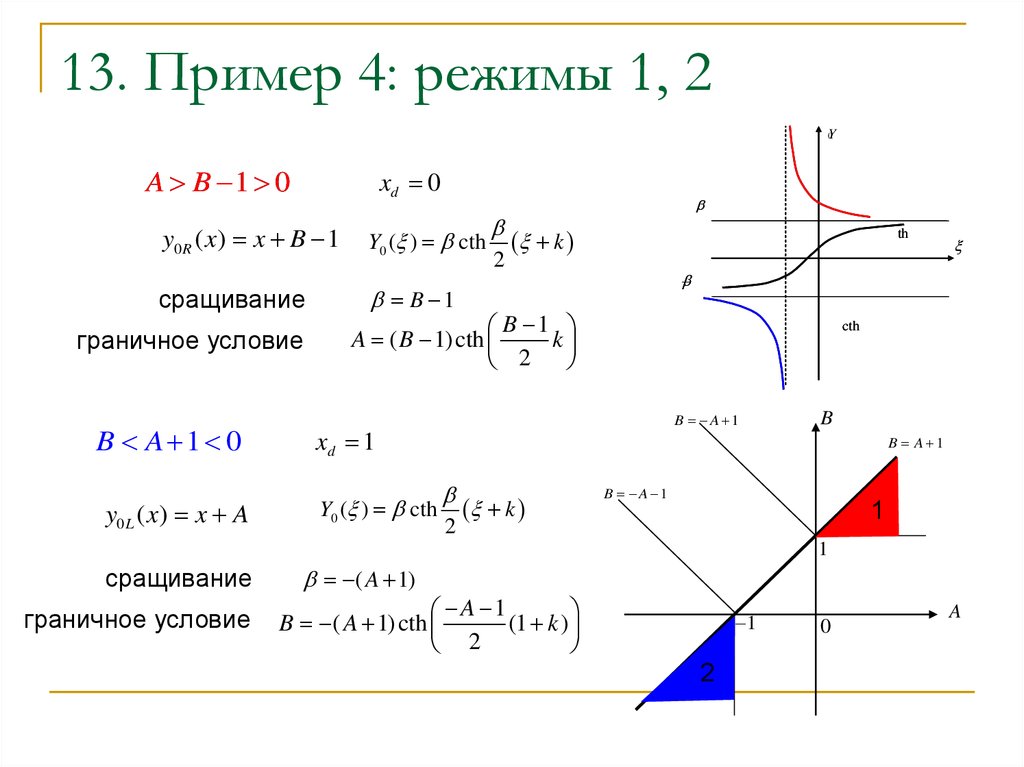
14. 13. Пример 4: режимы 1, 2

Y
0
A B 1 0
xd 0
y0 R ( x) x B 1
сращивание
граничное условие
B A 1 0
y0 L ( x) x A
Y0 ( ) cth
2
k
th
B 1
B 1
A ( B 1) cth
k
2
cth
B A 1
xd 1
Y0 ( ) cth
B
B A 1
2
k
B A 1
1
1
сращивание
граничное условие
( A 1)
A 1
B ( A 1) cth
(1 k )
2
1
2
0
A

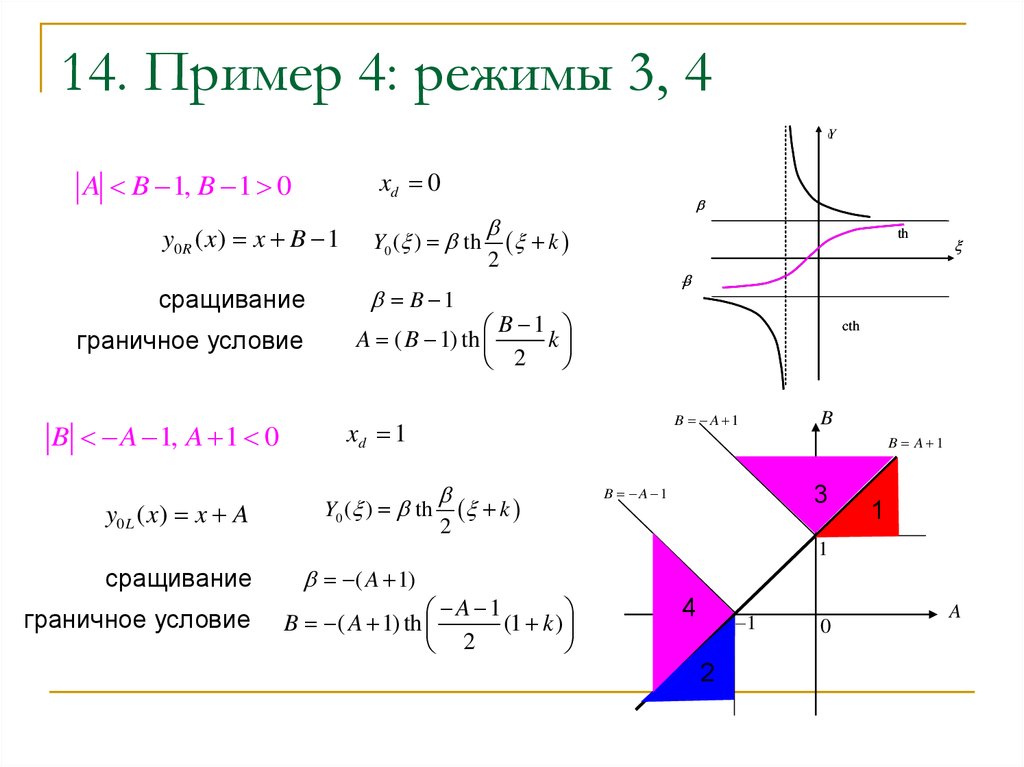
15. 14. Пример 4: режимы 3, 4

Y
0
xd 0
A B 1, B 1 0
y0 R ( x) x B 1
сращивание
граничное условие
B A 1, A 1 0
y0 L ( x) x A
Y0 ( ) th
2
k
th
B 1
B 1
A ( B 1) th
k
2
cth
B A 1
xd 1
Y0 ( ) th
B
B A 1
2
k
B A 1
3
1
1
сращивание
граничное условие
( A 1)
A 1
B ( A 1) th
(1 k )
2
4
1
2
0
A

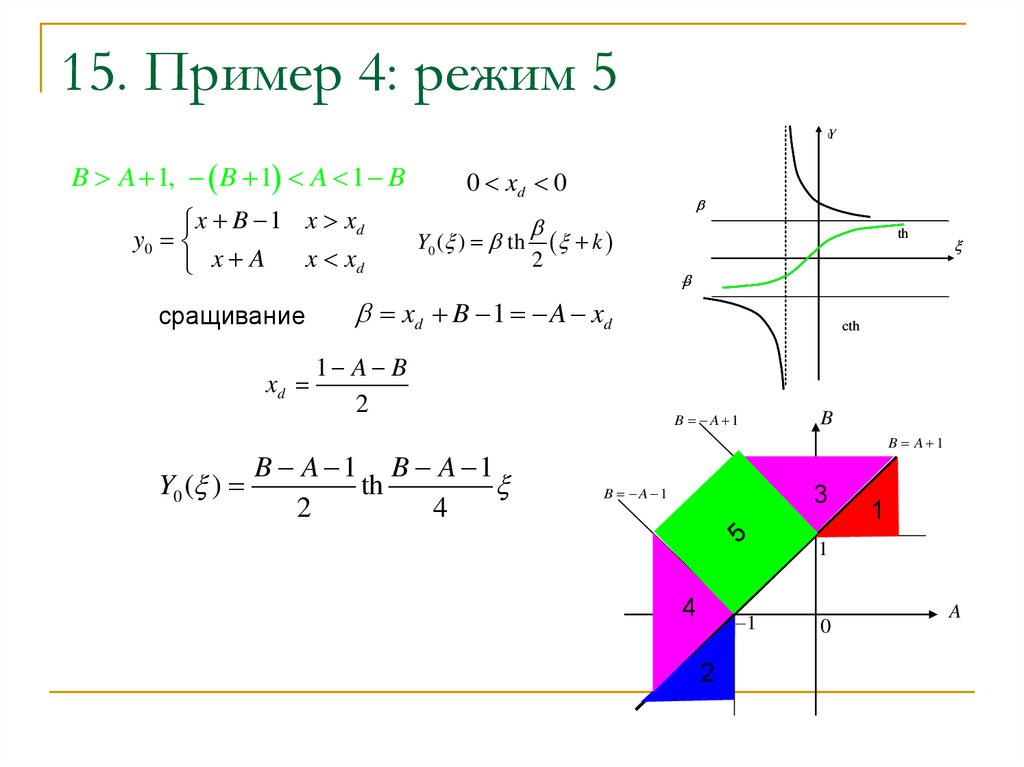
16. 15. Пример 4: режим 5

Y
0
B A 1, B 1 A 1 B
x B 1 x xd
y0
x xd
x A
сращивание
xd
Y0 ( )
0 xd 0
Y0 ( ) th
2
k
th
xd B 1 A xd
1 A B
2
B A 1 B A 1
th
2
4
cth
B A 1
B
B A 1
B A 1
3
1
1
4
1
2
0
A

17. 16. Упражнения к лекции 6

1.
Рассмотреть при
0 m 1, 0
0 x 1: x m y y 1,
2.
Рассмотреть задачу
задачу
y (0) 0
y x1/ 2 y y 1, 0 x 1
y (0) 0,
y (1) 1
Вначале найти перенормировку для пограничного слоя вблизи и
получить главный член внутреннего разложения. Далее найти
главный член внешнего разложения и срастить разложения
3. Определить где находятся погранслои и найти главные члены
внешнего и внутреннего разложений для задач
0 x 1: y y 1,
y (0) y (1) 0
1 x 1: y 2 y 1 y 2 0,
y ( 1) 1,
y (1) 1