Сращивание разложений. Подслои. Решение задачи. (Лекция 8)

1. Введение в асимптотические методы. Лекция 8

Сращивание разложений:
подслои

2. 1. Подслои

Рассматриваемая до сих пор схема: внешнее разложение + погранслой
не всегда достаточна. Погранслой сам может оказаться структурированным: содержать внутри себя подслои.
внешняя область
погранслой
подслой
Трехпалубная модель
Слои влияют друг на друга и построение решения в каждом из них
должно быть согласовано с построением решения в других слоях

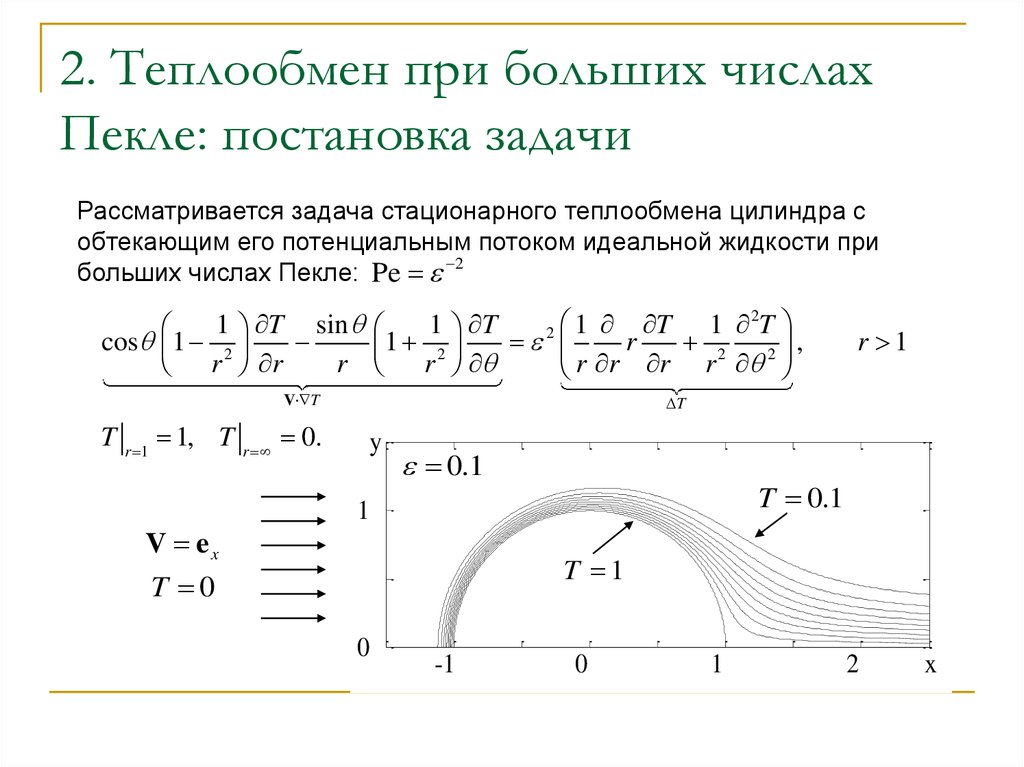
3. 2. Теплообмен при больших числах Пекле: постановка задачи

Рассматривается задача стационарного теплообмена цилиндра с
обтекающим его потенциальным потоком идеальной жидкости при
больших числах Пекле: Pe 2
1 T sin
1 T
T 1 2T
2 1
cos 1 2
r
2
,
1 2
2
r r
r r
r r r r
V T
T
r 1
1, T
V ex
r
0.
r 1
T
y
0.1
T 0.1
1
T 1
T 0
0
-1
0
1
2
x

4. 3. Внешнее разложение и толщина ПС

Внешнее разложение в главном члене
V T 0
Т постоянна вдоль линий тока
Т равна нулю вдоль любой линии тока при r
Толщина ПС
1
ПС координата
R
T 0
r 1
T
T
2 2T
2 R cos
2sin
O 2 2 O .
R
R
В погранслойных координатах обеспечивается баланс конвекции и
действующей по нормали к поверхности тела кондукции

5. 4. Внутреннее разложение: автомодельность

T0
T0 2T0
2 R cos
2sin
,
2
R
R
T0 R 0 1, T0 R 0.
Внутреннее разложение в главном члене
условие
сращивания
Ищем автомодельное решение задачи вида
T0 ( R, ) u( ), Rg ( )
2 R cos g ( )u 2 R sin g ( )u g 2 ( )u
g cos g sin
u
2R
2
u
g
u 2k u
Задача для
u( )
g cos g sin kg 3
Задача для
g ( )
kg
За счет нормировки
g
g g / k
всегда можно добиться чтобы k 1

6. 5. Внутреннее разложение: решение автомодельной задачи

u const e
u 2 u
Rg ( )
2
должна затухать при R
нужный знак - (+) при g>0 (g<0)
u C1 e d C2 , u(0) 1, u( ) 0
g 0
2
g 0
u( ) erfc
u( ) erfc
u( ) erfc
g cos g sin
g
g2
g sin 2sin
2
g
sin
sin
sin 2
2
g
2 C cos
sin
g
2
R sin
T erfc
2 C cos
g
sin
2 C cos
C 1
Константа С не определена. Для ее нахождения
нужно рассмотреть подслой вблизи критич. точки

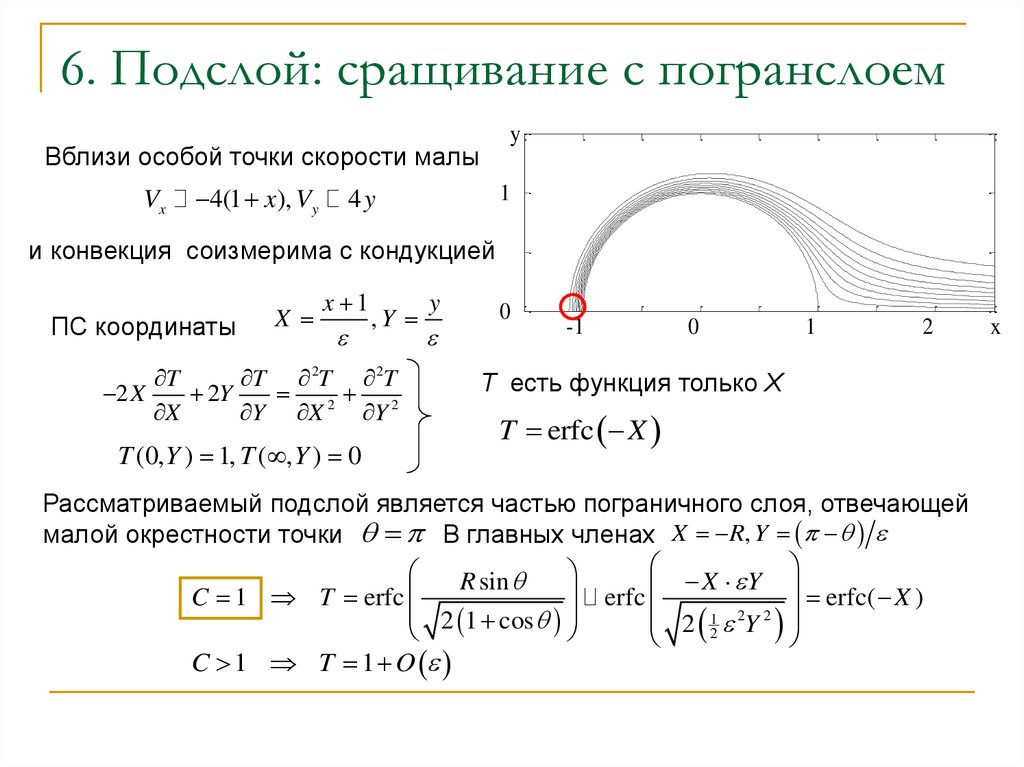
7. 6. Подслой: сращивание с погранслоем

y
Вблизи особой точки скорости малы
Vx
4(1 x), Vy
1
4y
и конвекция соизмерима с кондукцией
ПС координаты
X
x 1
,Y
T
T 2T 2T
2 X
2Y
X
Y X 2 Y 2
T (0, Y ) 1, T ( , Y ) 0
y
0
-1
0
1
2
T есть функция только X
T erfc X
Рассматриваемый подслой является частью пограничного слоя, отвечающей
малой окрестности точки В главных членах X R, Y
R sin
X
Y
erfc( X )
erfc
C 1 T erfc
2
2
2 1 Y
2 1 cos
2
C 1 T 1 O
x

8. 7. Динамический гистерезис: определя-ющее уравнение

7. Динамический гистерезис: определяющее уравнение
Изотермическая пульсация маленького пузырька с газом Ван-дер-Ваальса
p p(t ), (t ), T const
Равновесный (бесконечно медленный) процесс
p
жидкость
p P( )
Релаксационный закон для медленных процессов
время релаксации
p P( )
Задавая внешними условиями закон изменения давления p p0 (t ) получим ОДУ для нахождения
p P( )
неустойчивость
газ
P( ) p0 (t )
Характерная особенность – неустойчивость в области, где P ( ) 0
*
p p p*
p P( )
* P ( ) * 0
* A exp P ( )t

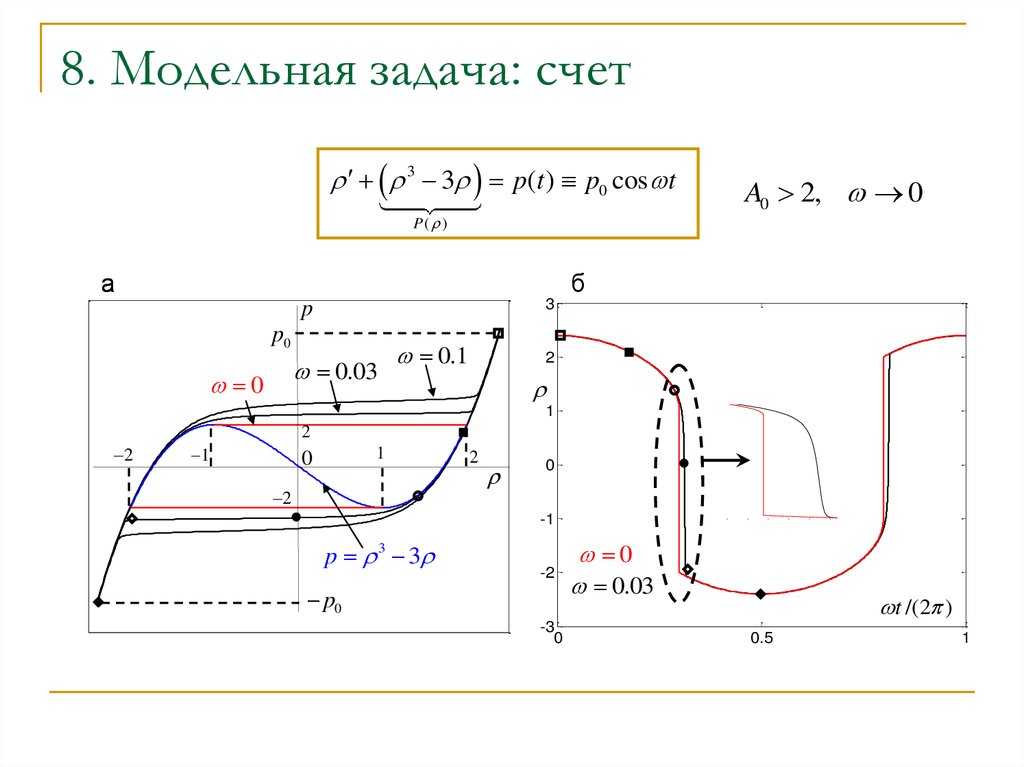
9. 8. Модельная задача: счет

3 3 p(t ) p0 cos t
A0 2, 0
P( )
а
б
3
p
p0
0.03
0
0.1
2
1
1
2
2
1
0.5
1
0
2
2
0
0
-0.5
-1
-1.5
-1
p 3 3
-2
p0
-3
0
-2
0.285
0.29
0.295
0.3
0
0.03
0.305
0.31
0.315
t /(2 )
0.5
1

10. 9. Медленная фаза

Перенормировка:
: 3 0 p0 cos T
3
0
T T0 : 0
1 :
3 3 p0 cos T
0 (T ) 1 (T )
Разложение:
0
T t
03 3 0
T arccos
p
0
1 B(T0 T )
0 3 02 1 3 1 0 1
2
T T0 arccos
p0
B 3 p0 sin T0 3 p02 4
0
3 02 1
1
12(T0 T )
Где разложение (1) перестает быть справедливым?
1/ 2
1
1
1 B1/ 2 1/ 2 t0 t
1 t0 t
12
T T0 : 1
(1)
t t0 T0 /
1/ 3
При этом оба члена 1/ 3
Соизмеримы, когда t0 t
Это дает нам нужную перенормировку для следующей фазы

11. 10. Промежуточная фаза

Перенормировка: t t0 9 B
:
, 1 B / 3
1/ 3
y y0 ( ) B / 9
1/ 3
Разложение:
0
1/ 3
y0 y 0
2
0
y y 2 B / 9
1/ 3
y
y3 0
y1 ( )
4
уравнение Рикатти
Сращивание
0
B / 3
1/ 3
1/ 3
0 1 B / 3
B / 3
2/3
1/ 3
B T0 T
1/2
y
y0 B / 3
y (- )
-4
-1
y -( - )
y y 2 0
1/ 2
: y
0 :
y0
0
0
Решение
=2.34
0
-8
-5
1
0
5

12. 11. Промежуточная фаза

1/ 3
:
y1 6 y1 y0 y03 0
0 : y0 0
1.5
1
1
0 : y1 0
0.5
2
0
1
1/ 3
1
-0.5
Где промежуточное разложение
перестает быть справедливым?
1 B / 3
1/ 3
B / 3
0
2/3
1
2
0
-1
-1.5
-2
0.03
0
Промежуточная
асимптотика
60
63
При этом все члены 1
Соизмеримы, когда 0 B / 3
Это дает нам нужную перенормировку для следующей фазы
1/ 3
66

13. 12.Быстрая фаза

( 1) 2 ( 2) O 2 / 3
t t* tnew ,
Перенормировка:
t :
Сращивание:
d
dt
2
( 1) ( 2)
Максимум скорости (максимальная
скорость фазового перехода) достигается
на этой фазе
при
1
1/ 3
1
1/ 3
1
0
12
1
3t
t0* T0 1 0 9 B
1 2
1
ln
t Const
9 1 3(1 )
d
dt
1
1
0.03
0 Внешнее решение
-1
Промежуточная фаза
Быстрая фаза
max
-2
Он не зависит от внешних условий
(констант p0 , в правой части уравнения)
60
61
62
63
64
65
66

14. 13.Плошадь петли гистерезиса

6
1
2
0
p
-2
-1
p
-6
-2
-2
-1
0
1
2
x
60
S ( ) S (0) 1 p
p p0 cos T0 ( 2 / 3 ) p0 cos T0 2 / 3
S ( ) S (0) 2/ 3
61
62
63
T0
64
65
T0
66
0
3
3B

15. 14. Упражнение к лекции 8

1.
Рассмотреть осесимметричную задачу о теплообмене сферы с
обтекающим ее потенциальным потоком идеальной жидкости при
больших значениях критерия Пекле
V T 2 T ,
T
r 1
1, T
r
r 1
0.
Используйте полярные координаты, в которых поле скоростей имеет вид
2.
1
2
Vr cos 1 3 , V sin 1 3 , V 0
r
r
Рассмотреть следующую «трехпалубную» задачу:
x 3 y 1 x 2 2 y 2 , 0 x 1
y (1) 1
Вычислить последовательно два члена внешнего, затем два члена
погранслойного, и наконец один член подслойного разложения.