Розвиток коаліцеподібних моделей в теорії корисності

1. Розвиток коаліцеподібних моделей в теорії корисності

РОЗВИТОК
КОАЛІЦЕПОДІБНИХ
МОДЕЛЕЙ В ТЕОРІЇ
КОРИСНОСТІ

2. Теорія корисності: історія та сучасність

ТЕОРІЯ КОРИСНОСТІ:
ІСТОРІЯ ТА СУЧАСНІСТЬ

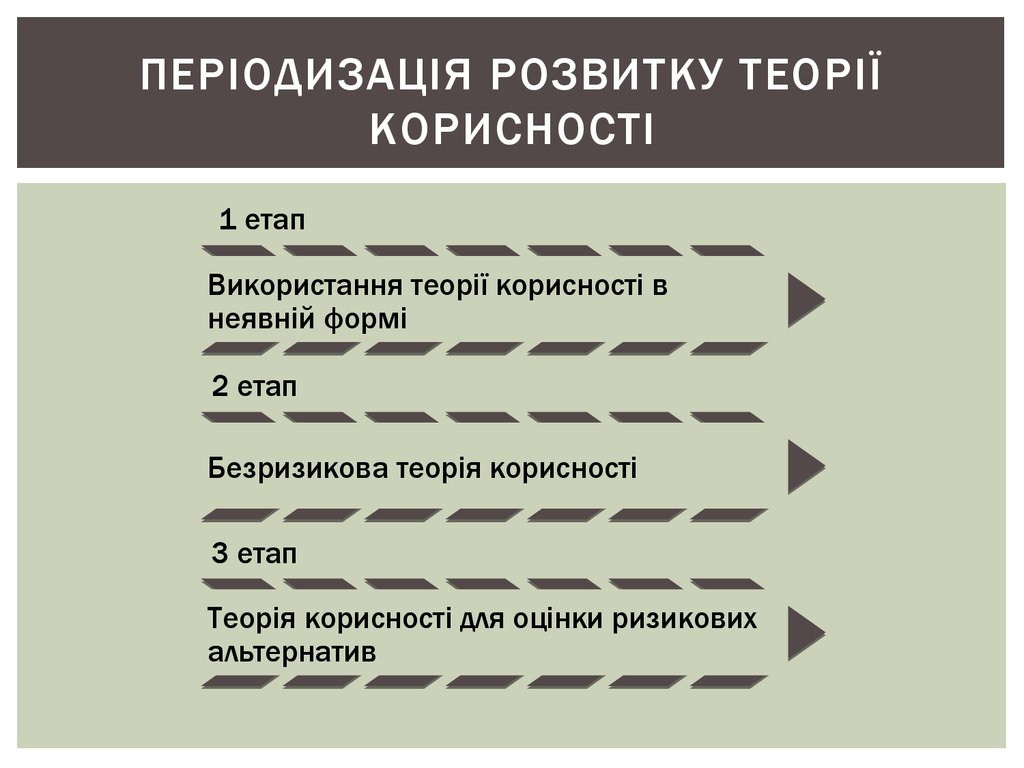
3. Періодизація розвитку теорії корисності

ПЕРІОДИЗАЦІЯ РОЗВИТКУ ТЕОРІЇ
КОРИСНОСТІ
1 етап
Використання теорії корисності в
неявній формі
2 етап
Безризикова теорія корисності
3 етап
Теорія корисності для оцінки ризикових
альтернатив

4. Періодизація розвитку теорії корисності

ПЕРІОДИЗАЦІЯ РОЗВИТКУ ТЕОРІЇ
КОРИСНОСТІ
Безризикова теорія корисності
1
• Аналіз вибору індивіда в
умовах повної визначеності
2
• Виведення функції
корисності та побудова на її
основі функції попиту
3
• Широке використання
інструментарію кривих
байдужості
Теорія корисності для аналізу
ризикових альтернатив
1
2
3
• Використання ризику для оцінки
уподобань індивіда
• Прогнозування поведінки
індивіда в умовах ризику
• Використання модифікованого
інструментарію кривих
байдужості

5. Основні моделі сучасної теорії корисності

ОСНОВНІ МОДЕЛІ СУЧАСНОЇ ТЕОРІЇ
КОРИСНОСТІ
Теорія
 
сподіваної корисності:
Теорія перспектив:
Порядково-залежна теорія сподіваної корисності:

6. Проблеми сучасної теорії очікуваної корисності

ПРОБЛЕМИ СУЧАСНОЇ
ТЕОРІЇ ОЧІКУВАНОЇ
КОРИСНОСТІ

7. Невідповідність передбачень теорії та результатів експериментів

НЕВІДПОВІДНІСТЬ ПЕРЕДБАЧЕНЬ ТЕОРІЇ
ТА РЕЗУЛЬТАТІВ ЕКСПЕРИМЕНТІВ
Сучасна теорія корисності прагне пояснити
поведінку індивіда в умовах ризику та
визначити базові характеристики (принципи)
на яких ґрунтується оцінка ризикових
альтернатив індивідом.

8. Базові принципи сучасної теорії корисності

БАЗОВІ ПРИНЦИПИ СУЧАСНОЇ ТЕОРІЇ
КОРИСНОСТІ
1. 
Принцип ідемпотентності
Сутність принципу ідемпотентності полягає в
еквівалентності:
2. Принцип або ефект коаліціонування
Ефект
коаліціонування
проявляється
в
еквівалентності для індивіда двох лотерей
виду:

9. Ефект розщеплення подій (Event splitting effect, ese)

ЕФЕКТ РОЗЩЕПЛЕННЯ ПОДІЙ (EVENT
SPLITTING EFFECT, ESE)
Альтернативним
до
принципу
коаліціонування є припущення про ефект
розщеплення подій. В рамках транзитивних
моделей теорії корисності припущення про
коаліціонування та ефект розщеплення подій
є взаємовиключними.

10. Види коаліціонування

ВИДИ КОАЛІЦІОНУВАННЯ
 
Для
тригілкової лотереї за умови :
Верхнє коаліціонування:
В рамках ESE моделей
Нижнє коаліціонування:
В рамках ESE моделей:

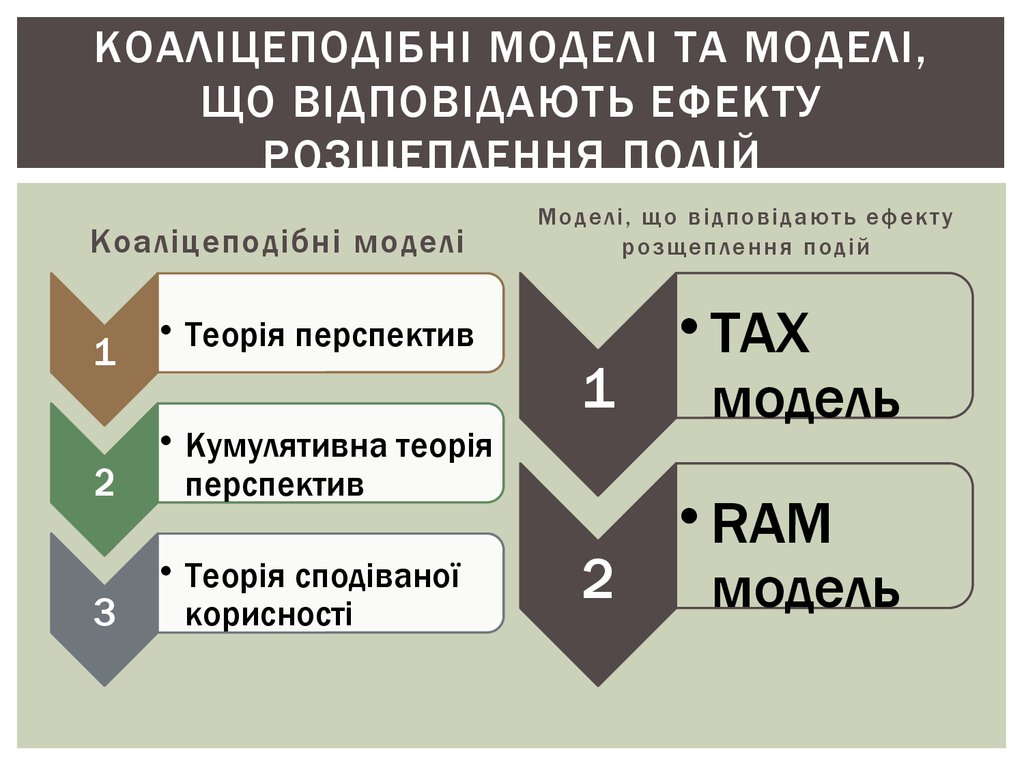
11. Коаліцеподібні моделі та моделі, що відповідають ефекту розщеплення подій

КОАЛІЦЕПОДІБНІ МОДЕЛІ ТА МОДЕЛІ,
ЩО ВІДПОВІДАЮТЬ ЕФЕКТУ
РОЗЩЕПЛЕННЯ ПОДІЙ
Коаліцеподібні моделі
1
Моделі, що відповідають ефекту
розщеплення подій
1
• TAX
модель
2
• RAM
модель
• Теорія перспектив
2
• Кумулятивна теорія
перспектив
3
• Теорія сподіваної
корисності

12. Критика коаліцеподібних моделей

КРИТИКА КОАЛІЦЕПОДІБНИХ МОДЕЛЕЙ
Критика коаліцеподібного класу моделей
ведеться з позиції неможливості пояснення в
рамках існуючих моделей даного класу ряду
емпірично виявлених феноменів:
Відхилення від стохастичного домінування
першого порядку
Відхилення
від
верхньої
та
нижньої
кумулятивної незалежності
Інше

13. Стохастичне домінування першого порядку (first stochastic order dominance, fsd)

СТОХАСТИЧНЕ ДОМІНУВАННЯ ПЕРШОГО
ПОРЯДКУ (FIRST STOCHASTIC ORDER
DOMINANCE, FSD)
 
Стохастичне домінування першого
порядку означає виконання нестрогої
нерівності (із перетворенням її на строгу
нерівність принаймні для одного ):
,
де
означає імовірність того, що
можливий результат лотереї буде більше
ніж

14. Експерименти М. Бірнбаума та Р. Наваррети

ЕКСПЕРИМЕНТИ М. БІРНБАУМА ТА Р.
НАВАРРЕТИ
  М.
Бірнбаум та Р. Наваррета провели серію
експериментів, в яких показали, що існує стійка
тенденція до порушення FSD що не може бути пояснена
в рамках існуючих моделей коаліцеподібного класу.
Базова лотерея:
Розщеплення нижньої гілки базової лотереї (має
зробити її менш бажаною в рамках ESE):
Розщеплення верхньої гілки базової лотереї (має
зробити її більш бажаною в рамках ESE)

15. Експерименти М. Бірнбаума та Р. Наваррети

ЕКСПЕРИМЕНТИ М. БІРНБАУМА ТА Р.
НАВАРРЕТИ
  рамках існуючих коаліцеподібних моделей (PT,
В
CPT, RDEU) має виконуватися співвідношення:
Крім того лотерея домінує лотерею в плані FSD.
Оскільки імовірність отримати 14$ або більше в
обох лотереях однакова – 95%, 90$ або більше
також однакова (95%), а 96$ в лотереї складає
95% а в – 90%.
Але емпірична перевірка показала, що близько
70% учасників експериментів обирають лотерею

16. Double rank dependent expected utility (DRDEU модель)

DOUBLE RANK
DEPENDENT EXPECTED
UTILITY (DRDEU
МОДЕЛЬ)

17. Ґенеза DRDEU моделі

ҐЕНЕЗА DRDEU МОДЕЛІ
Базові принципи подвійної порядково залежної
моделі
сподіваної
корисності
(Double
Rank
Dependent Expected Utility, DRDEU):
1.Індивід оцінює найменший результат як
гарантований (референтна точка)
2.Індивід оцінює не абсолютну величину інших
потенційних результатів, а величину збільшення
гарантованого
результату
(на
скільки
він
збільшиться). Тобто оцінюються різниці між
результатами

18. Функціональна форма DRDEU моделі

ФУНКЦІОНАЛЬНА ФОРМА DRDEU
МОДЕЛІ
При впорядкуванні потенційних результатів в
порядку неспадання:
 
DRDEU модель можна представити як:
При чому , а при дорівнює 0.

19. Редукція DRDEU моделі до інших моделей коаліцеподібного класу

РЕДУКЦІЯ DRDEU МОДЕЛІ ДО ІНШИХ
МОДЕЛЕЙ КОАЛІЦЕПОДІБНОГО КЛАСУ
 
За умови лінійності функції корисності
DRDEU модель редукується до форми RDEU
За умови лінійності функції зваження
імовірності DRDEU модель редукується до
форми SUT
За умови
та лінійності функції
корисності DRDEU модель редукується до
форми EUT

20. Пояснення в рамках DRDEU моделі відхилення від стохастичного домінування першого порядку

ПОЯСНЕННЯ В РАМКАХ DRDEU МОДЕЛІ
ВІДХИЛЕННЯ ВІД СТОХАСТИЧНОГО
ДОМІНУВАННЯ ПЕРШОГО ПОРЯДКУ
М. Бірнбаум показав, що FSD еквівалентно
одночасному виконанню трьох припущень:
1. Транзитивність
2. Монотонність за виходом
3. Коаліціонування
Відповідно, для того, щоб модель передбачала
можливість відхилення від FSD вона повинна
порушувати принаймні одне з базових
припущень.

21. Пояснення в рамках DRDEU моделі відхилення від стохастичного домінування першого порядку

ПОЯСНЕННЯ В РАМКАХ DRDEU МОДЕЛІ
ВІДХИЛЕННЯ ВІД СТОХАСТИЧНОГО
ДОМІНУВАННЯ ПЕРШОГО ПОРЯДКУ
Моделі, запропоновані М. Бірнбаумом
пояснюють відхилення від FSD шляхом
порушення
принципу
коаліціонування
(відповідно це моделі ESE класу).
Натомість DRDEU модель може пояснити
відхилення від FSD завдяки можливості
порушення принципу монотонності

22. Пояснення в рамках DRDEU моделі відхилення від стохастичного домінування першого порядку

ПОЯСНЕННЯ В РАМКАХ DRDEU МОДЕЛІ
ВІДХИЛЕННЯ ВІД СТОХАСТИЧНОГО
ДОМІНУВАННЯ ПЕРШОГО ПОРЯДКУ
При
  використанні стандартних умов для функції корисності:
U ( x) x
0.88
Та для функції зваження ймовірностей:
0,724 p 0, 61
w( p )
0,724 p 0, 61 (1 p ) 0,61
Модель DRDEU відповідає емпіричним даним М. Бірнбаума та
Р. Наваррета

23. Допоміжні інструменти в аналізі дескриптивної сили моделей в теорії корисності

ДОПОМІЖНІ ІНСТРУМЕНТИ В АНАЛІЗІ
ДЕСКРИПТИВНОЇ СИЛИ МОДЕЛЕЙ В
ТЕОРІЇ КОРИСНОСТІ
 
Міра Бірнбаума:
- теоретична частка індивідів які оберуть
лотерею
Коефіцієнт
обчислюють шляхом проведення
«тестових» серій попарного порівняння альтернатив
які демонструють стійке співвідношення

24. Порівняння ефективності DRDEU з існуючими моделями

ПОРІВНЯННЯ ЕФЕКТИВНОСТІ DRDEU З
ІСНУЮЧИМИ МОДЕЛЯМИ
Коаліц
еподіб
ні
моделі
Ті що відповідають
верхньому
коаліціонуванню
Ті що відповідають
нижньому
коаліціонуванню
Моделі, що відповідають ефекту
розщеплення подій
Ідемпотентні моделі
GDU (4) - 7919
CPT (4) - 12000
CPT (4) - 12000
RAM (5) – 2466
RAM (4) – 6938
TAX (3) – 4868

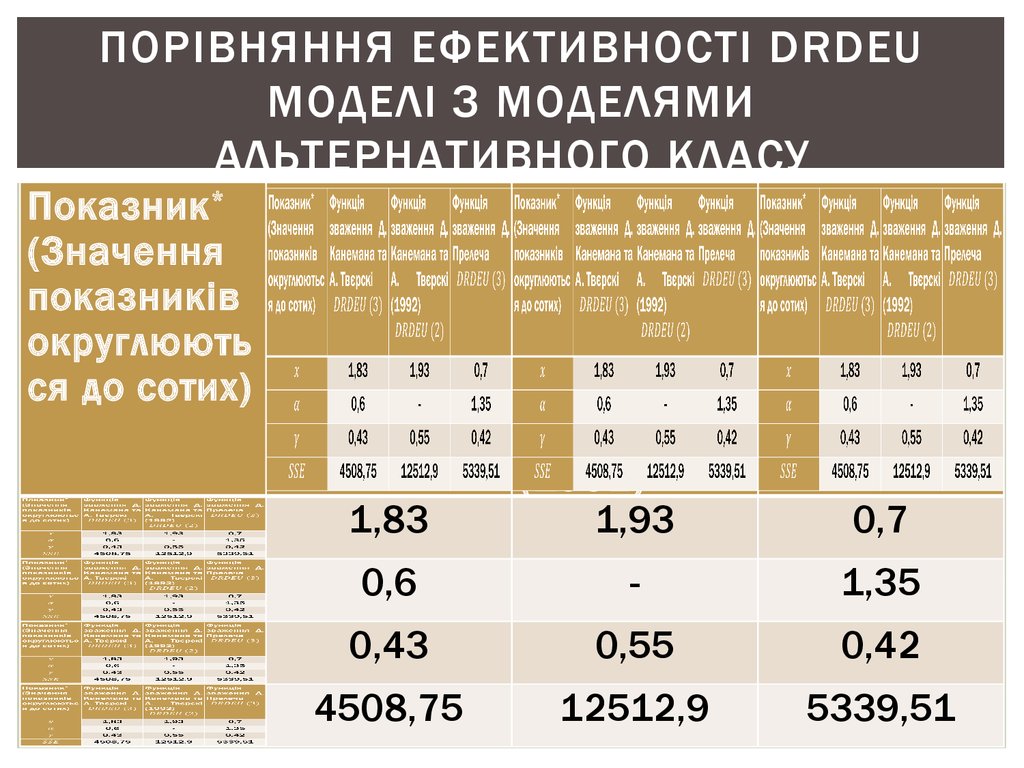
25. Порівняння ефективності DRDEU моделі з моделями альтернативного класу

ПОРІВНЯННЯ ЕФЕКТИВНОСТІ DRDEU
МОДЕЛІ З МОДЕЛЯМИ
АЛЬТЕРНАТИВНОГО КЛАСУ
Показник *
(Значення
показників
округлюють
ся до сотих)
Функція
зваження
Д.
Канемана
та
А.
Твєрскі
1,83
1,83
0,6
0,6
0,43
0,43
4508,75
Функція
Функція
зваження
зваження
Д.
Д. Прелеча
Канемана
та
А.
Твєрскі
(1992)
1,93
0,7
1,93
0,7
1,35
1,35
0,55
0,42
0,55
0,42
12512,9
5339,51

26. Теоретичне обґрунтування ефекту коаліціонування

ТЕОРЕТИЧНЕ ОБҐРУНТУВАННЯ ЕФЕКТУ
КОАЛІЦІОНУВАННЯ
 
Теорема.
Необхідною умовою для виникнення
ефекту розщеплення подій в скінченних
– гілкових лотереях з додатними
виходами в транзитивних ідемпотентних
моделях теорії корисності є порушення
аксіоми незалежності в слабкій формі ().

27. Апробація DRDEU моделі у вирішення задач прикладного характеру

АПРОБАЦІЯ DRDEU
МОДЕЛІ У ВИРІШЕННЯ
ЗАДАЧ ПРИКЛАДНОГО
ХАРАКТЕРУ

28. Використання DRDEU моделі у моделюванні систем контролю

ВИКОРИСТАННЯ DRDEU МОДЕЛІ У
МОДЕЛЮВАННІ СИСТЕМ КОНТРОЛЮ
 
Розглянемо проблему сплати / ухиляння
від сплати для споживача блага як гру
виду:

29. Додаткові припущення

ДОДАТКОВІ ПРИПУЩЕННЯ
 
Сума штрафу пропорційна вартості блага ,
імовірність бути перевіреним:
Де
– число перевірок,
– кількість актів
споживання блага, – інтенсивність використання
блага.
– чисельність споживачів блага
– вартість проведення однієї перевірки для
компанії

30. Оптимізаційна задача

ОПТИМІЗАЦІЙНА ЗАДАЧА
 
- прибуток компанії у випадку використання
стратегії тотального контролю.
- прибуток компанії у випадку стратегії
вибіркового контролю.

31. Оптимізаційна задача з урахуванням додаткових параметрів

ОПТИМІЗАЦІЙНА ЗАДАЧА З
УРАХУВАННЯМ ДОДАТКОВИХ
ПАРАМЕТРІВ
 

32. Приклад постановки задачі

ПРИКЛАД ПОСТАНОВКИ ЗАДАЧІ
 
Припустімо,
що розподіл інтенсивності використання
здійснюється за нормальним законом розподілу з
параметрами ( та ), з вартістю перевірки , , , , (в
такому випадку
– кількість рейсів на день,
–
пасажиропотік/день, – вартість квитка, – штраф за
безквитковий проїзд (виражений у вартості квитків)).
В такому випадку більш вигідною для компанії є
використання
стратегії (це дозволить отримати
додатковий прибуток в сумі 1238.13) з кількістю
перевірок , та з невиплатами вартості проїзду 25
пасажирами.