Классификация поверхностей с использованием определителя

1.

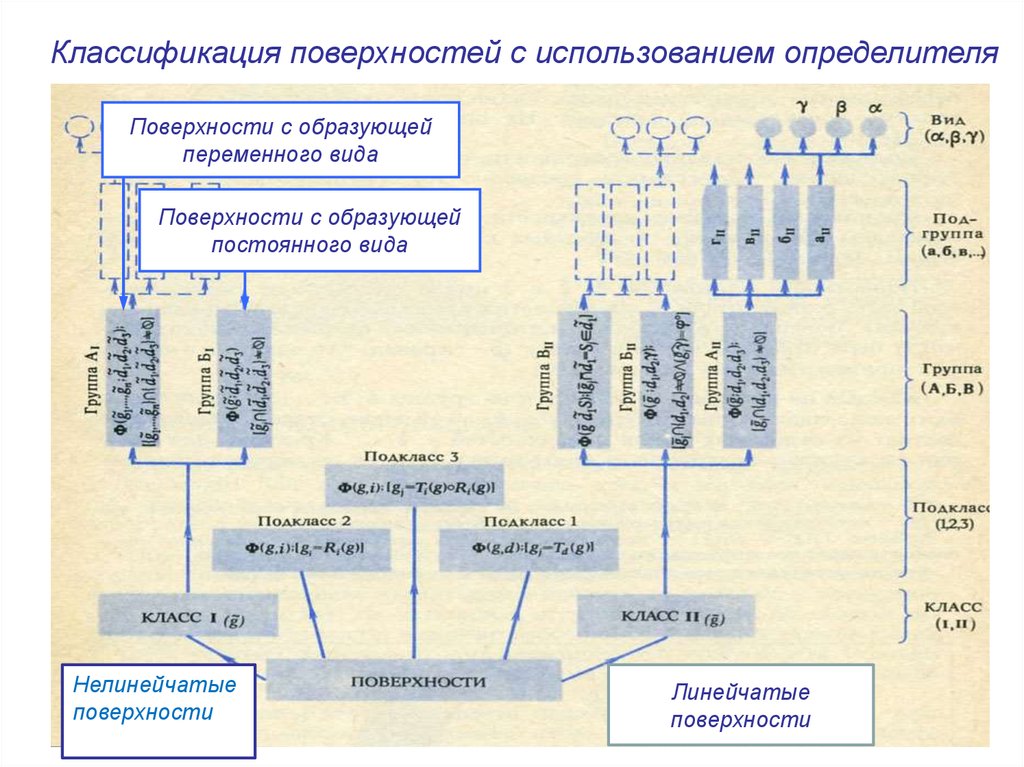
Классификация поверхностей с использованием определителя
Поверхности с образующей
переменного вида
Поверхности с образующей
постоянного вида
Нелинейчатые
поверхности
Линейчатые
поверхности

2.

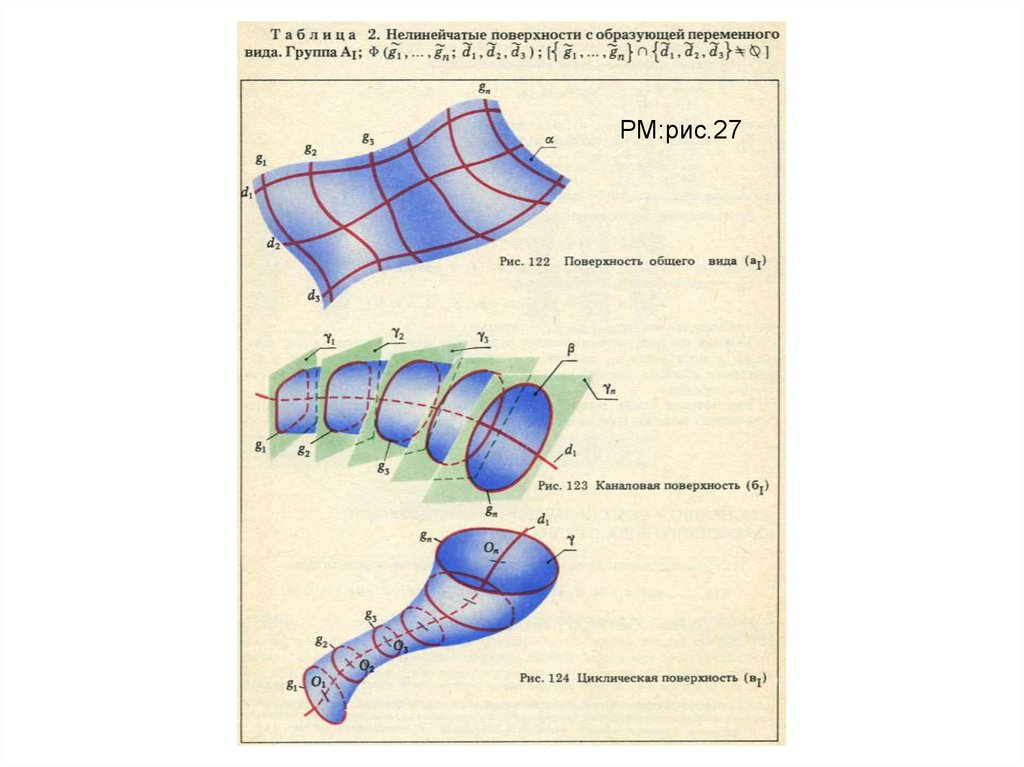
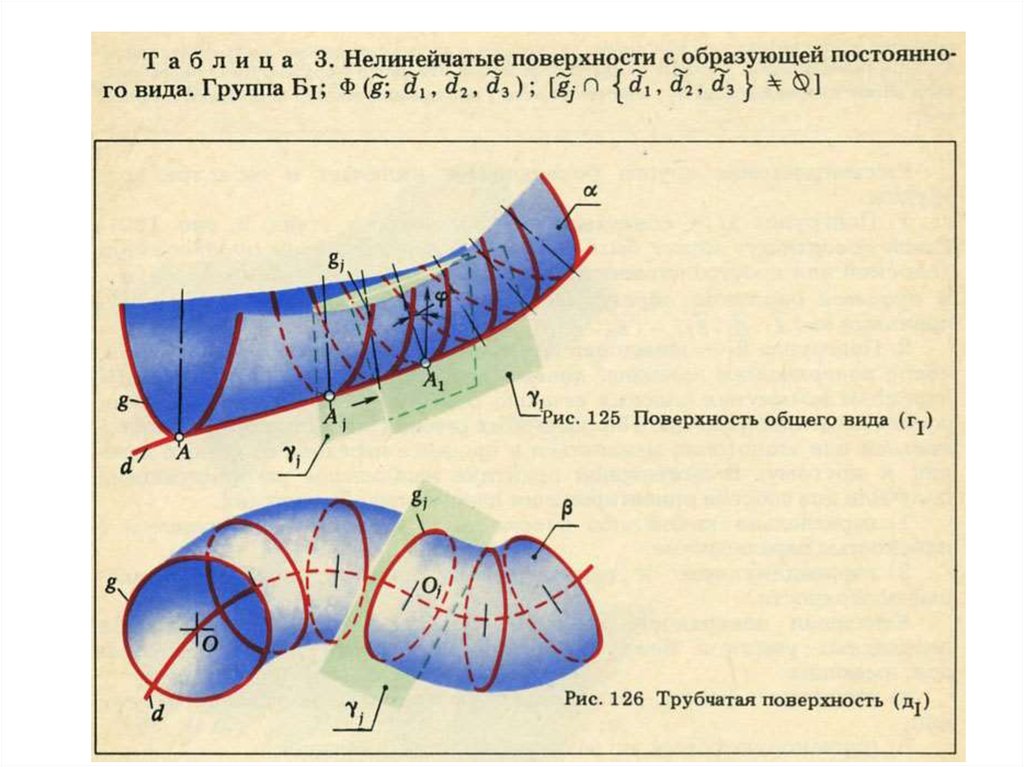
РМ:рис.27

3.

4.

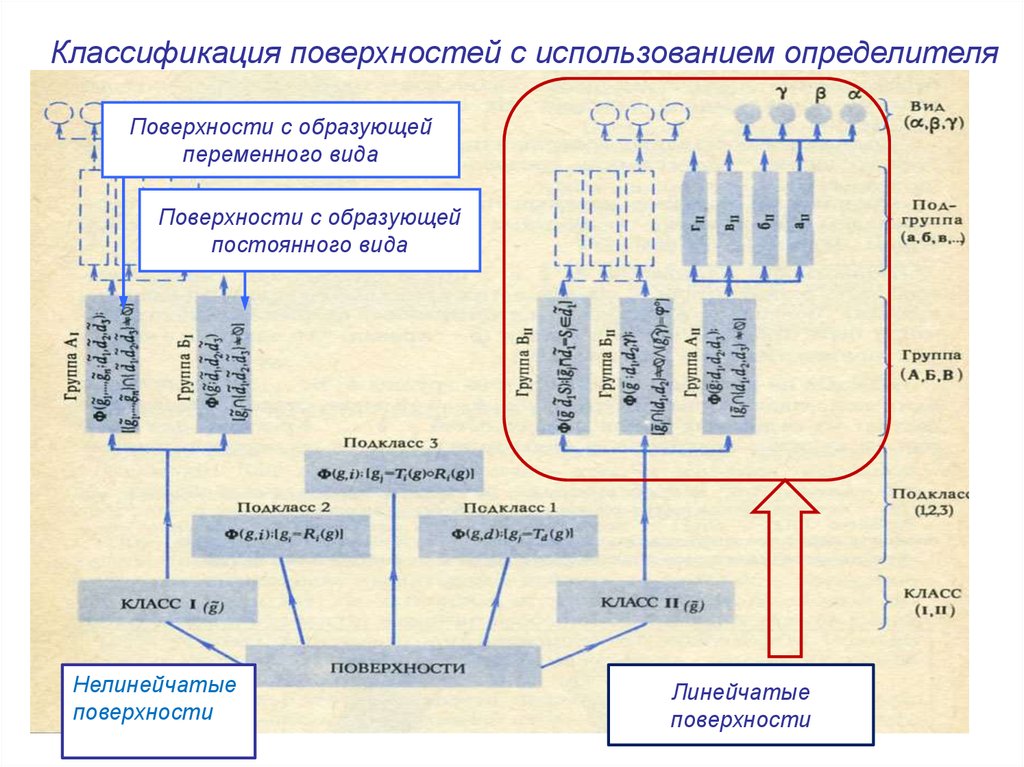
Классификация поверхностей с использованием определителя
Поверхности с образующей
переменного вида
Поверхности с образующей
постоянного вида
Нелинейчатые
поверхности
Линейчатые
поверхности

5.

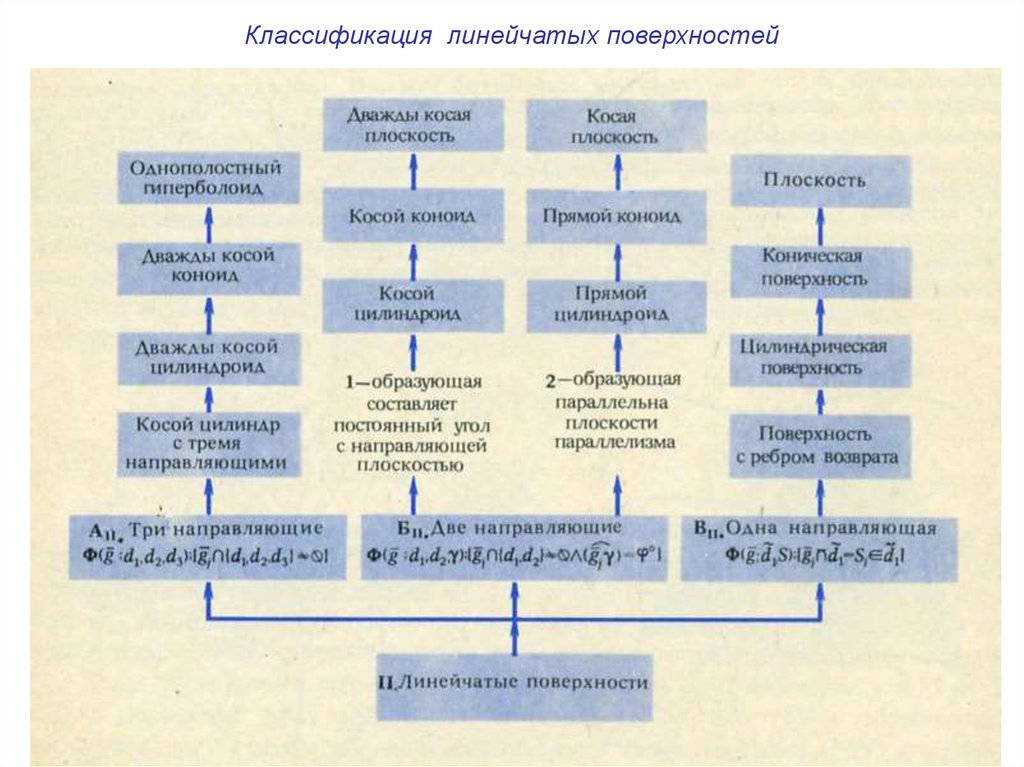
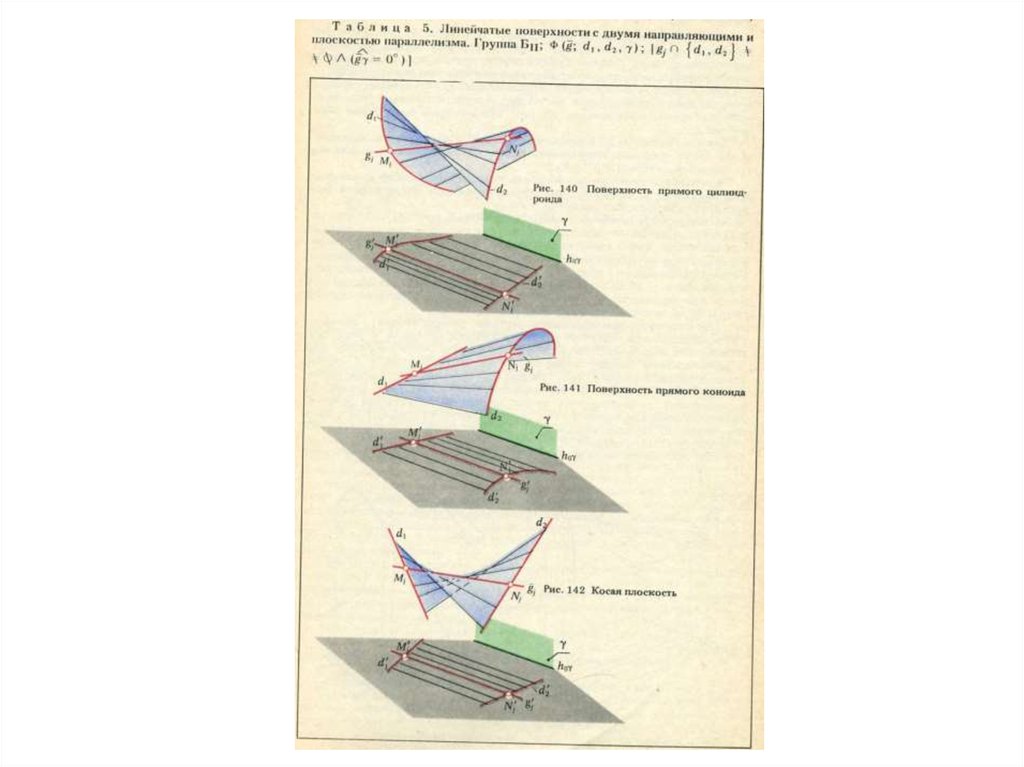
Классификация линейчатых поверхностей

6.

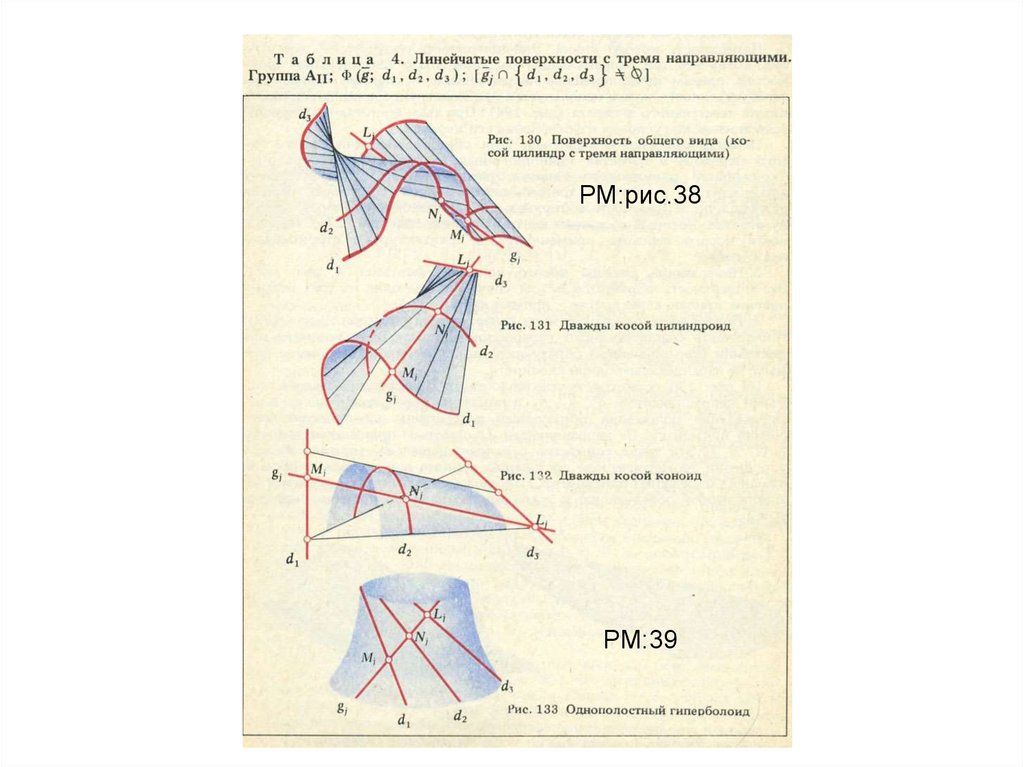
РМ:рис.38
РМ:39

7.

8.

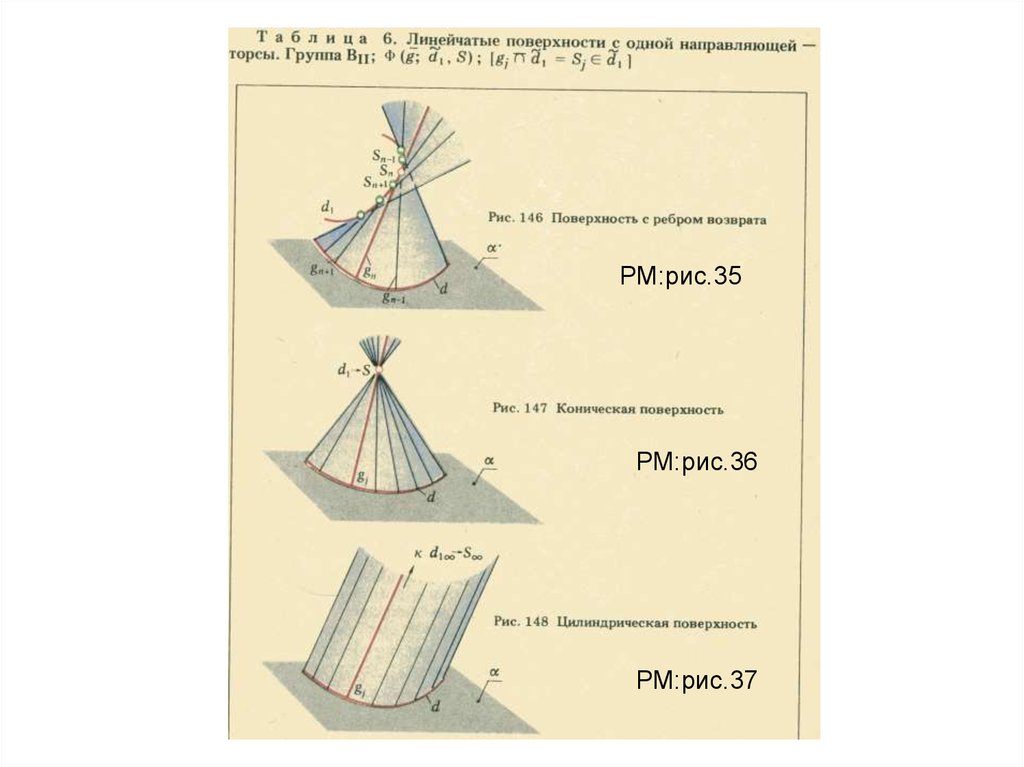
РМ:рис.35
РМ:рис.36
РМ:рис.37

9.

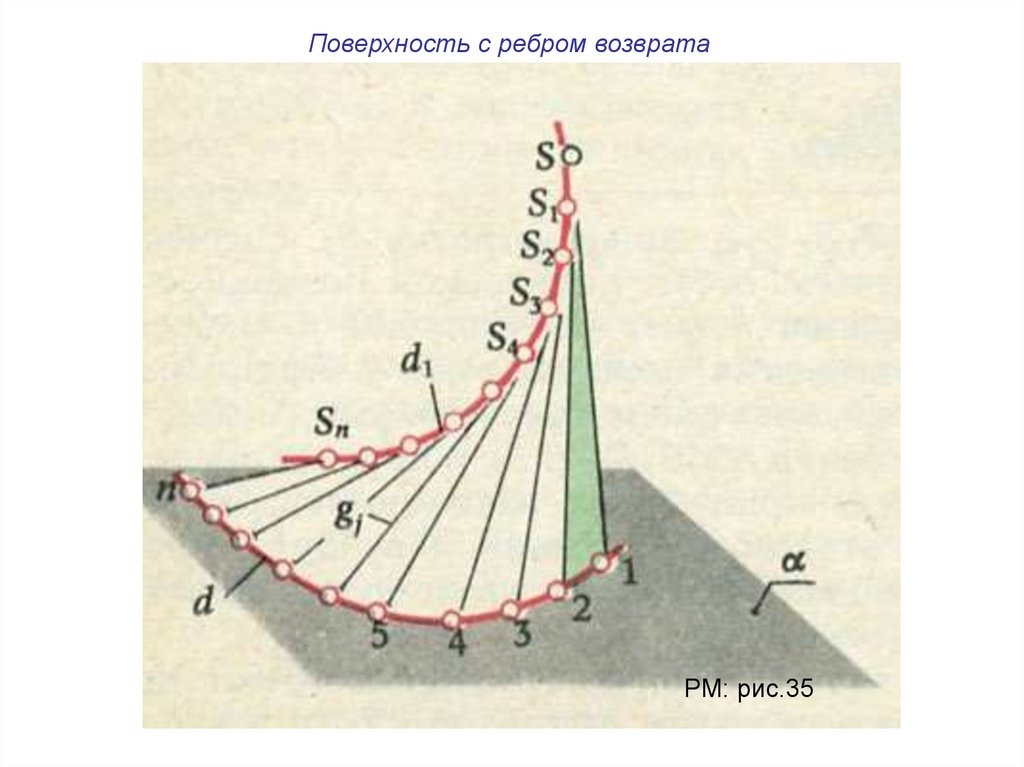
Поверхность с ребром возврата
РМ: рис.35

10.

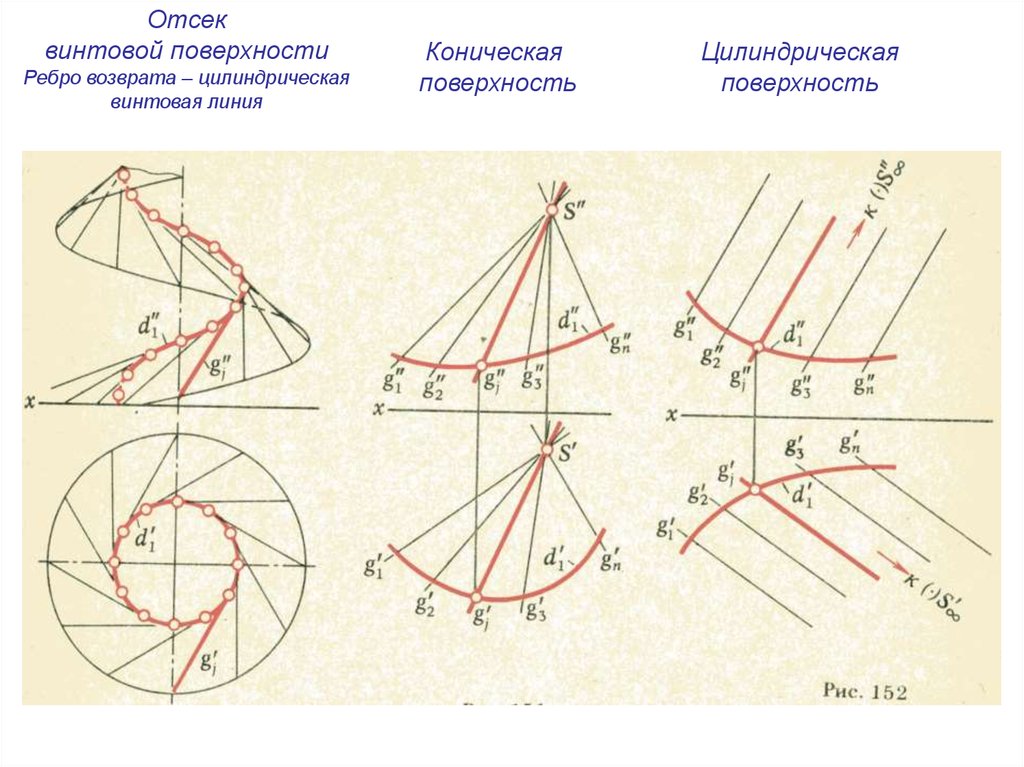
Отсек
винтовой поверхности
Ребро возврата – цилиндрическая
винтовая линия
Коническая
поверхность
Цилиндрическая
поверхность

11.

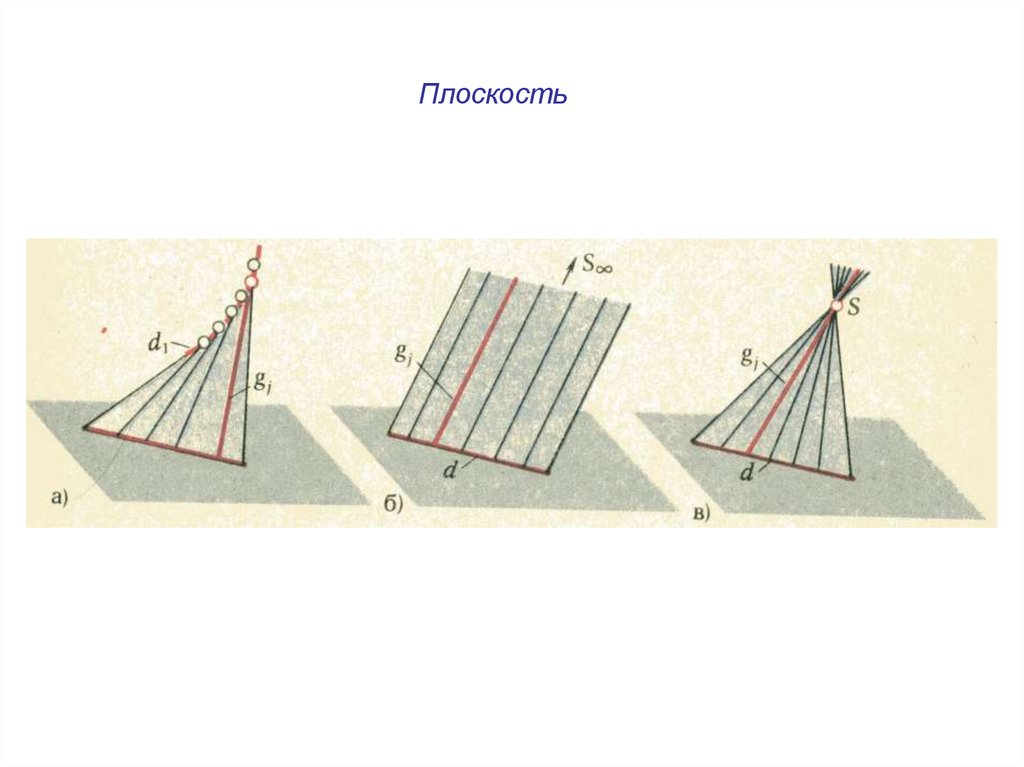
Плоскость

12.

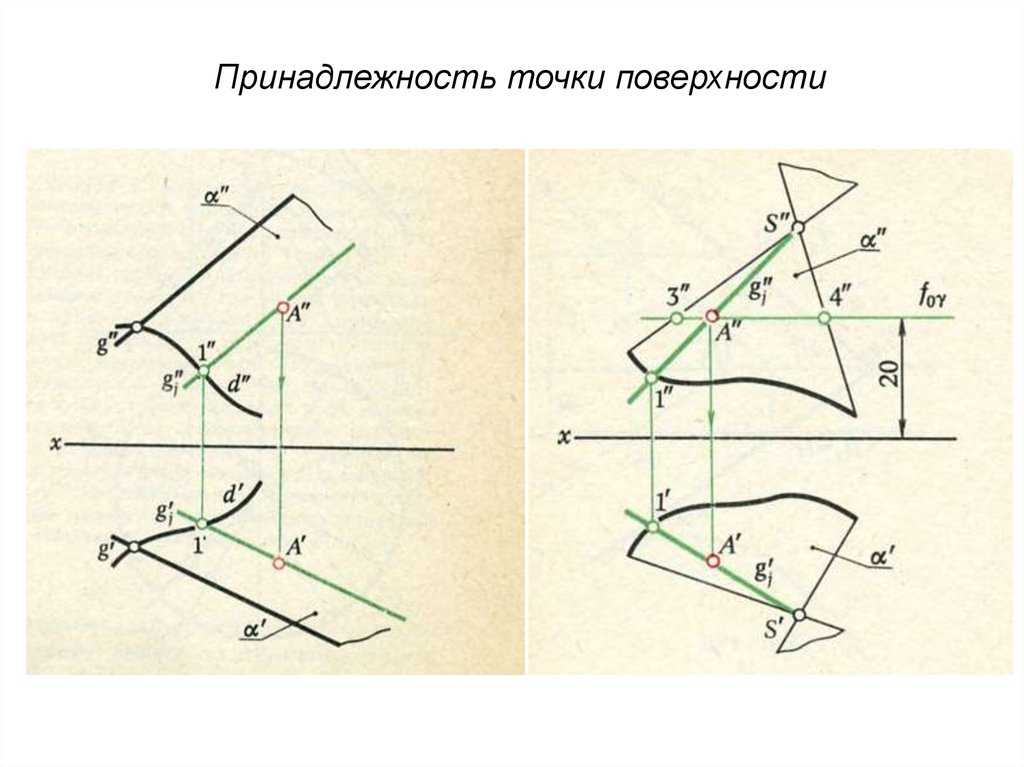
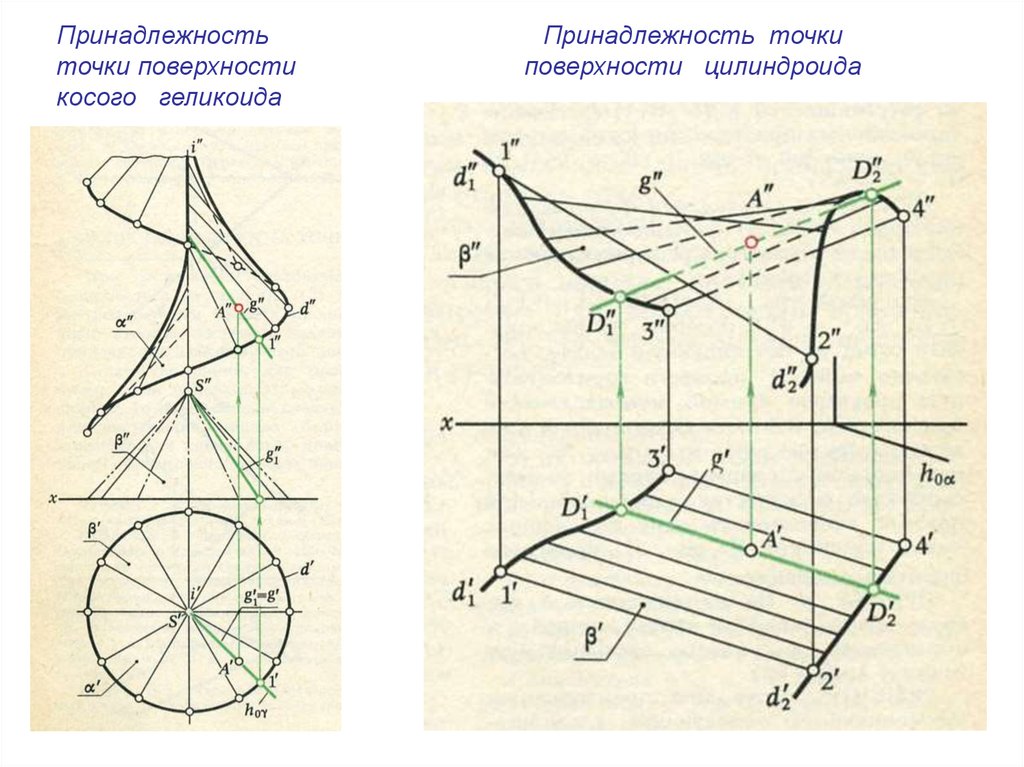
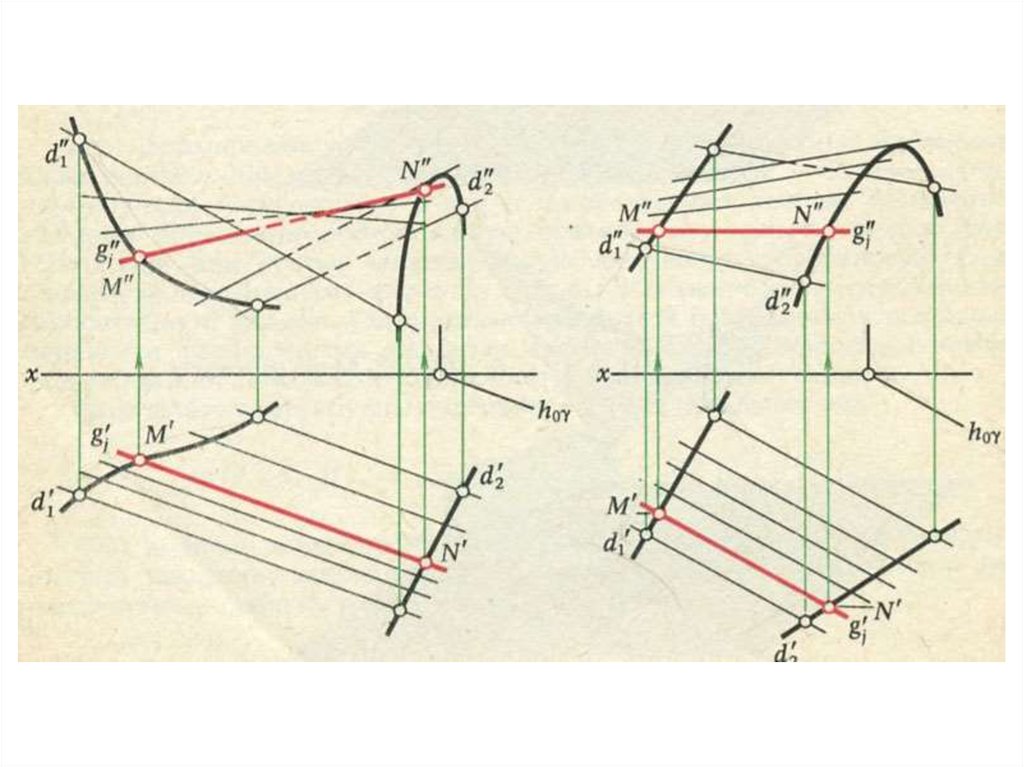
Принадлежность точки поверхности

13.

Принадлежность
точки поверхности
косого геликоида
Принадлежность точки
поверхности цилиндроида

14.

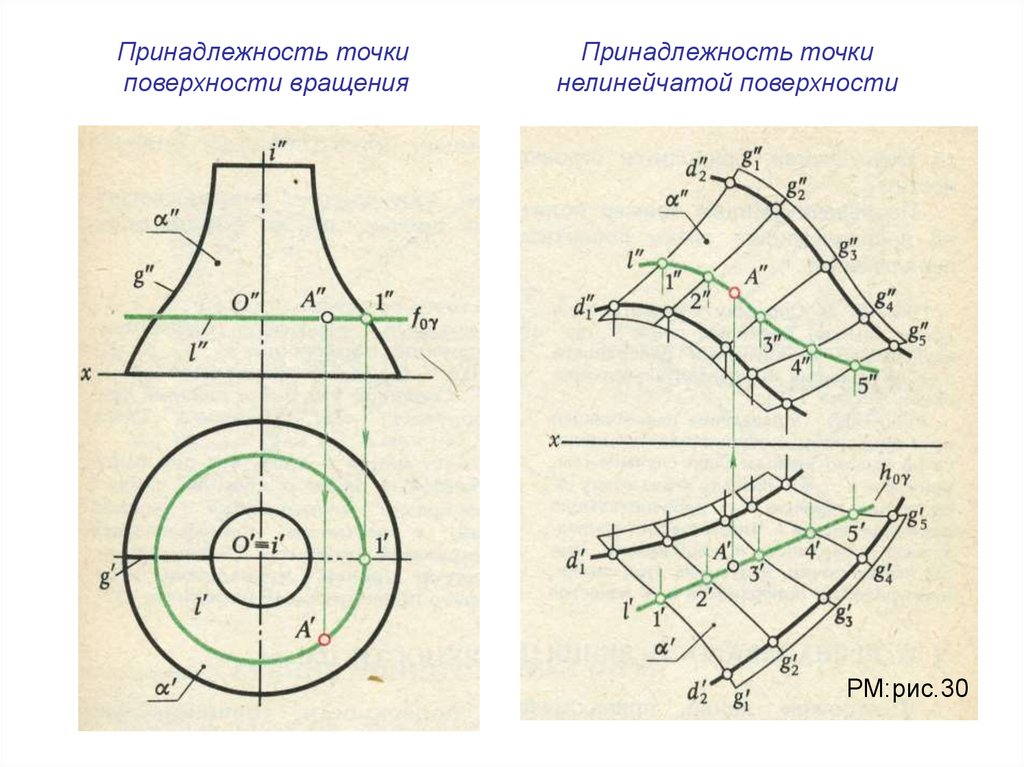
Принадлежность точки
поверхности вращения
Принадлежность точки
нелинейчатой поверхности
РМ:рис.30

15.

16.

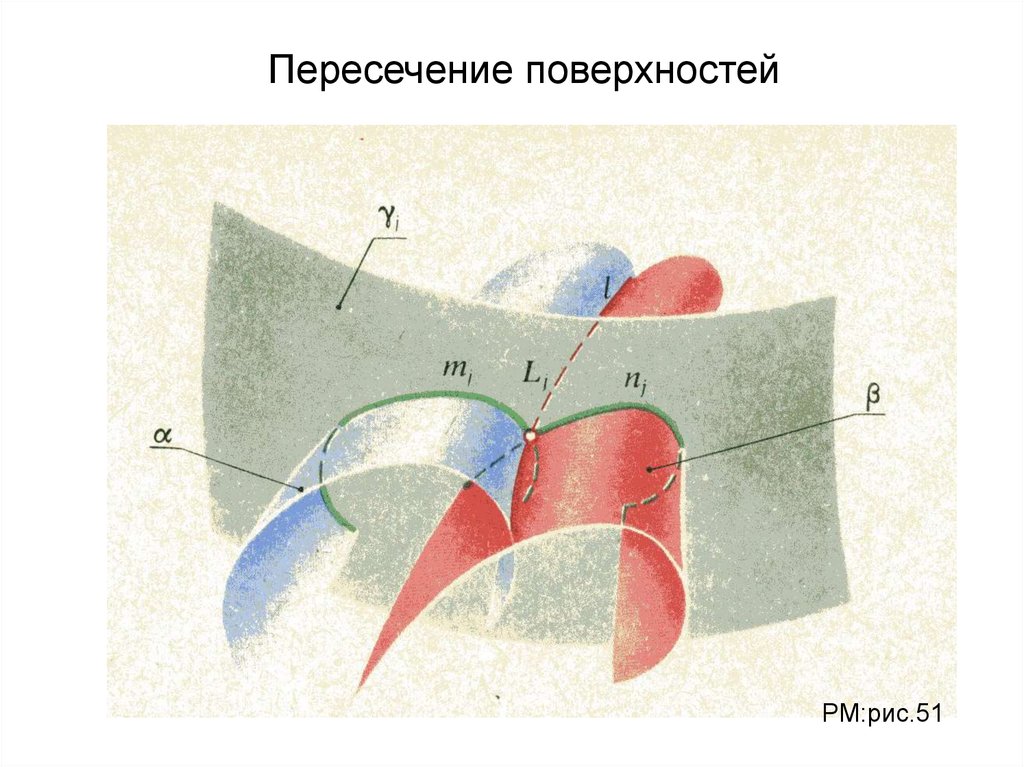
Пересечение поверхностей
РМ:рис.51

17.

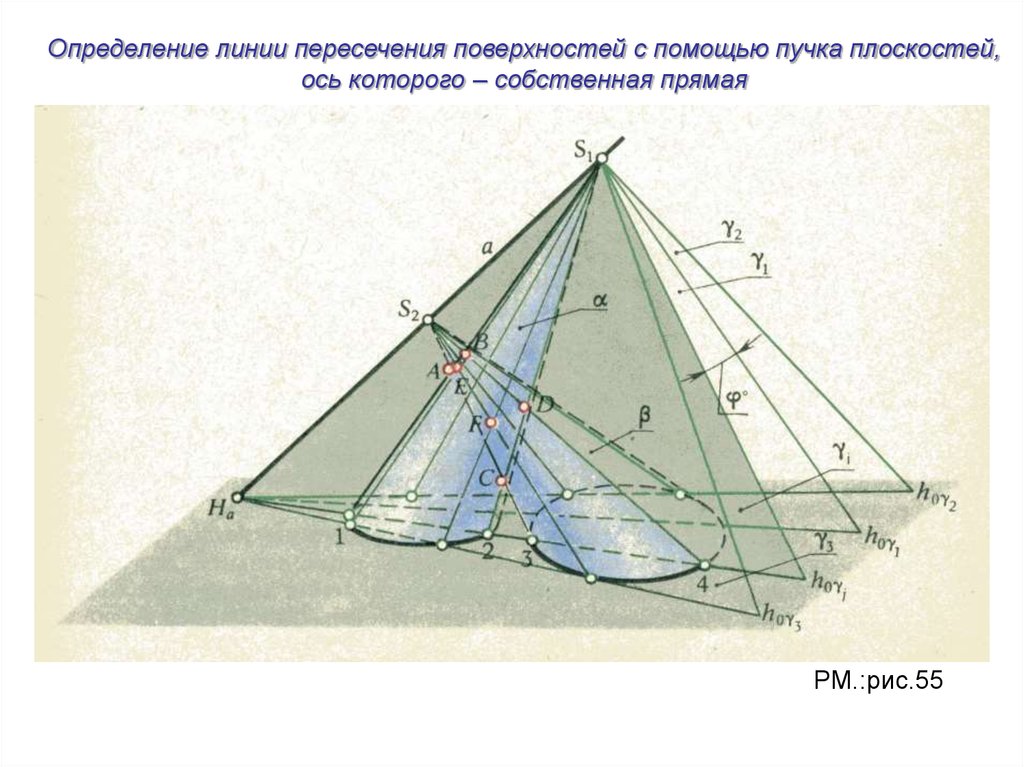
Определение линии пересечения поверхностей с помощью пучка плоскостей,
ось которого – собственная прямая
РМ.:рис.55

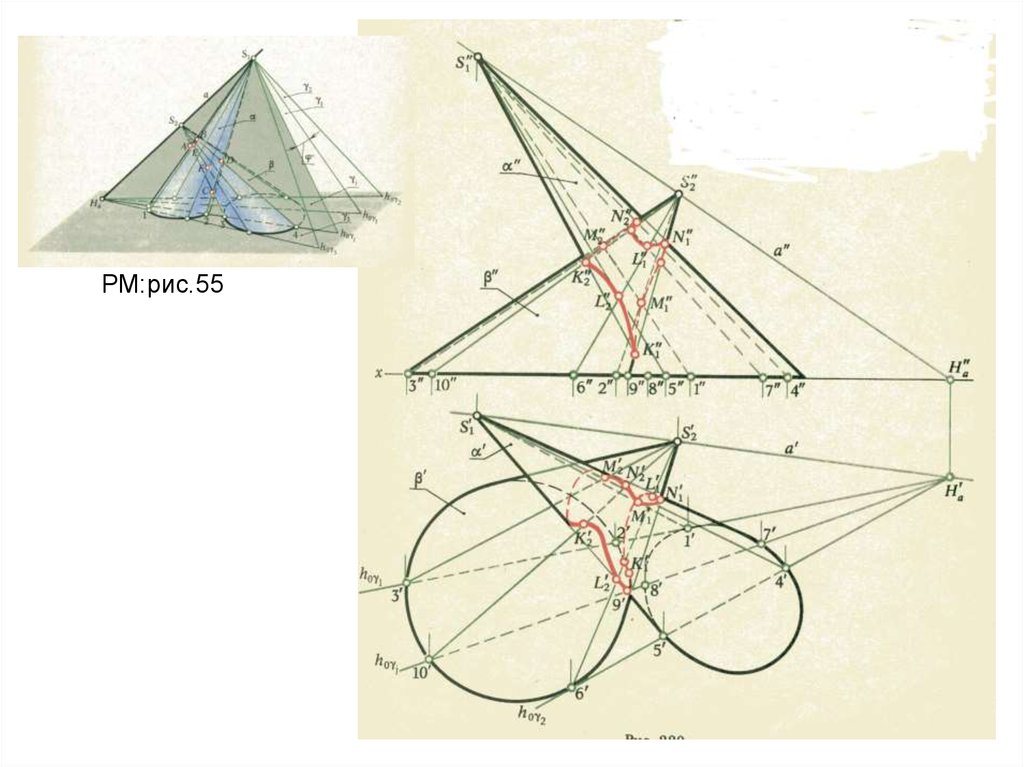
18.

РМ:рис.55

19.

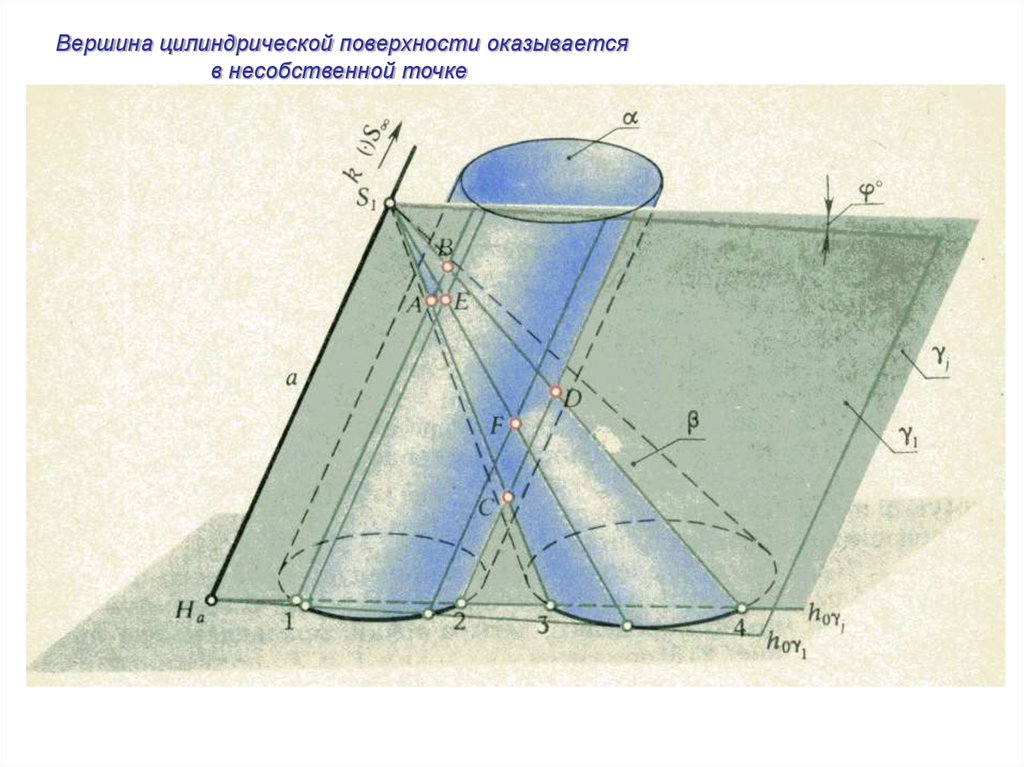
Вершина цилиндрической поверхности оказывается
в несобственной точке

20.

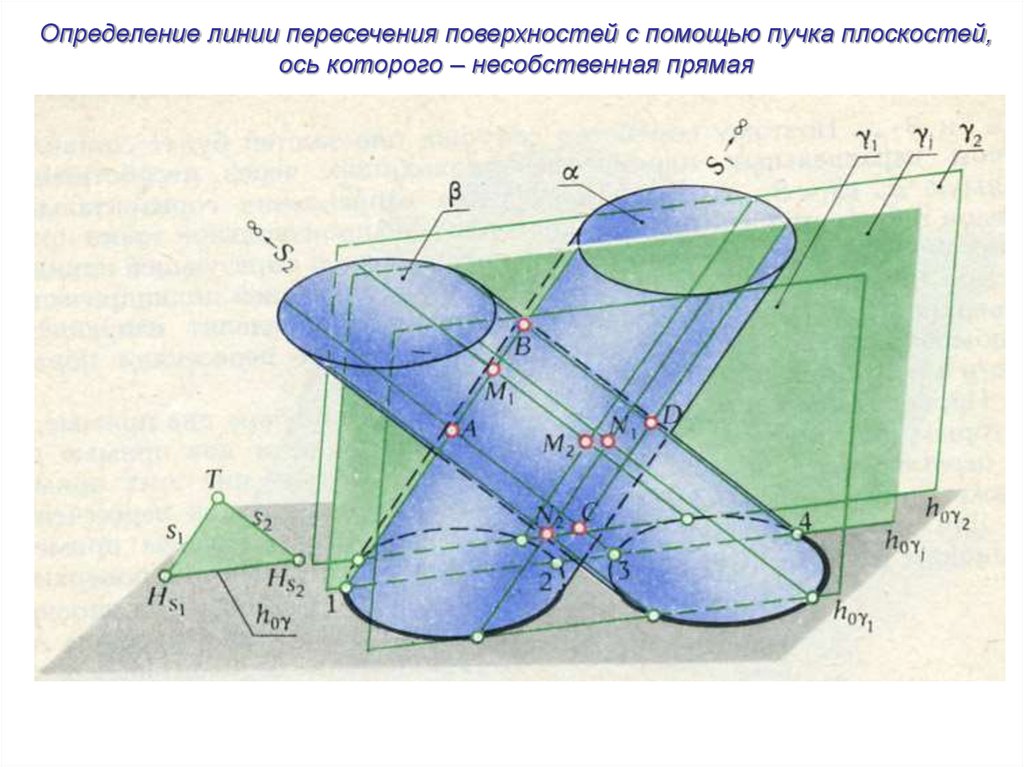
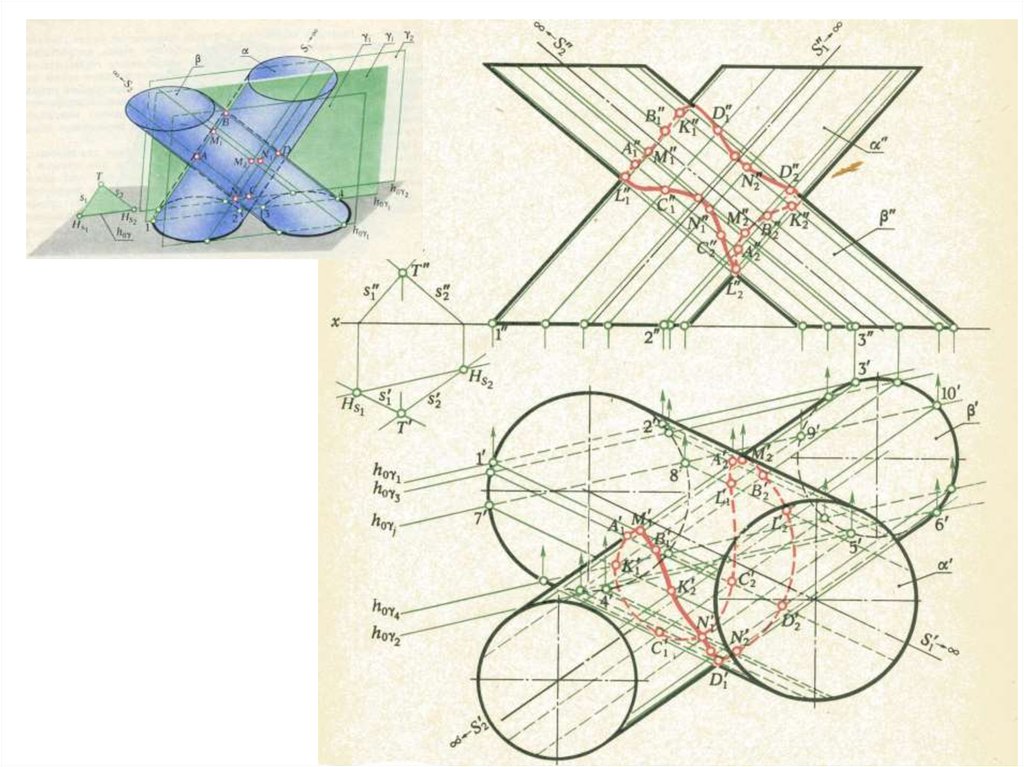
Определение линии пересечения поверхностей с помощью пучка плоскостей,
ось которого – несобственная прямая

21.

22.

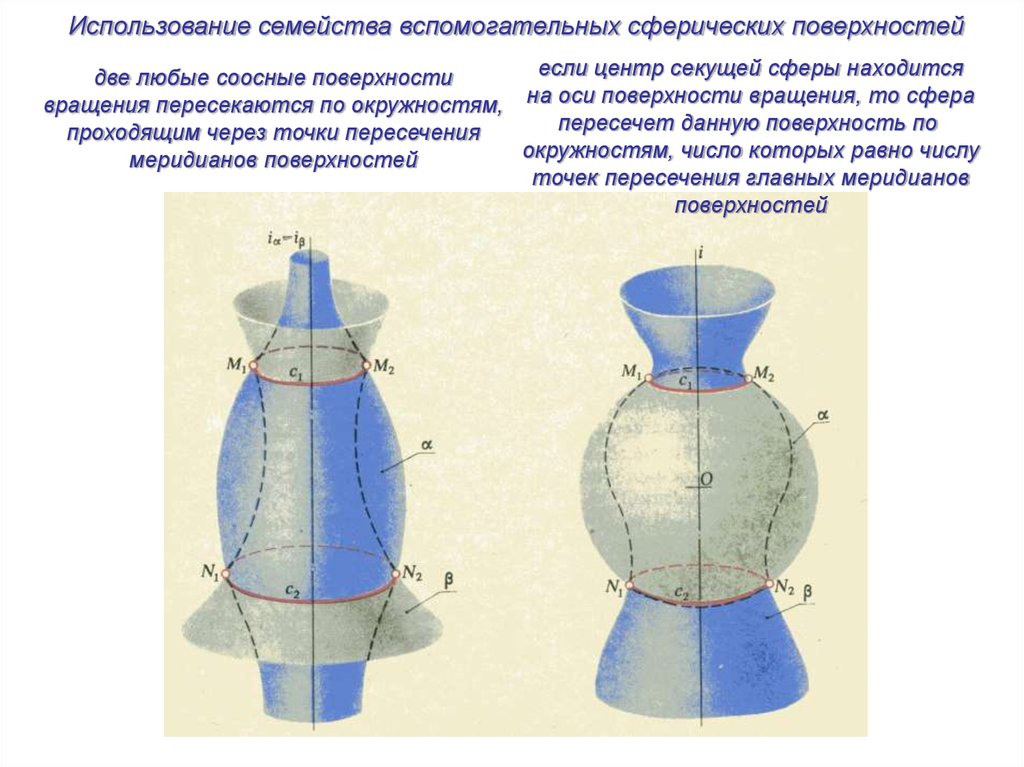
Использование семейства вспомогательных сферических поверхностей
если центр секущей сферы находится
две любые соосные поверхности
вращения пересекаются по окружностям, на оси поверхности вращения, то сфера
пересечет данную поверхность по
проходящим через точки пересечения
окружностям, число которых равно числу
меридианов поверхностей
точек пересечения главных меридианов
поверхностей

23.

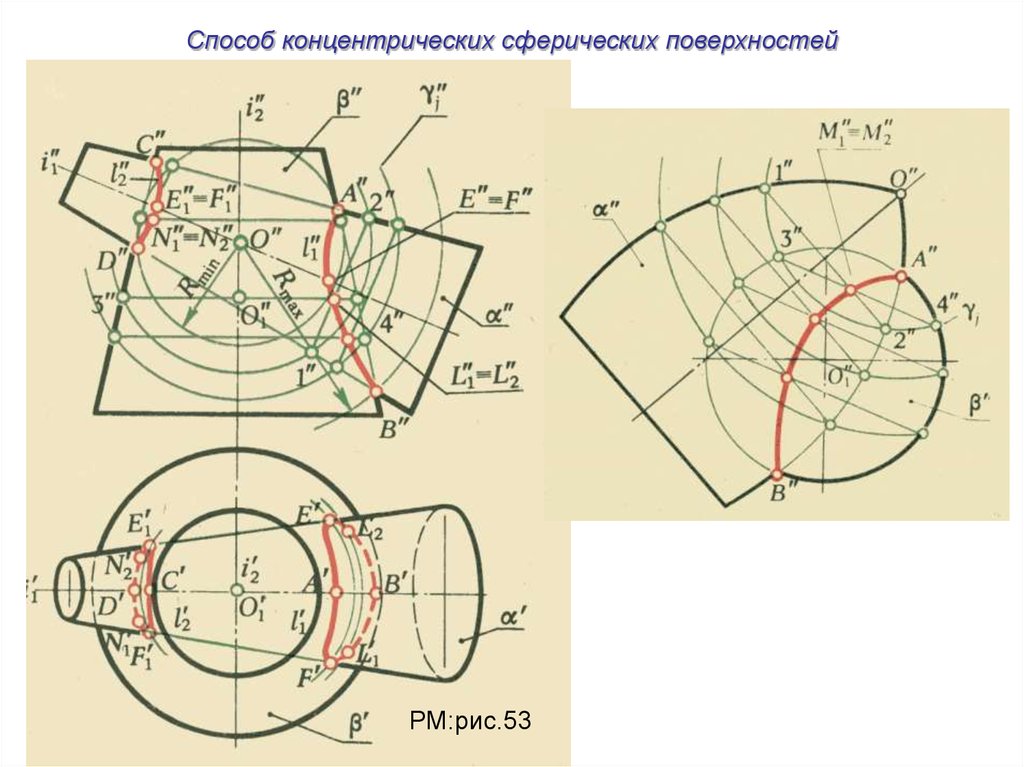
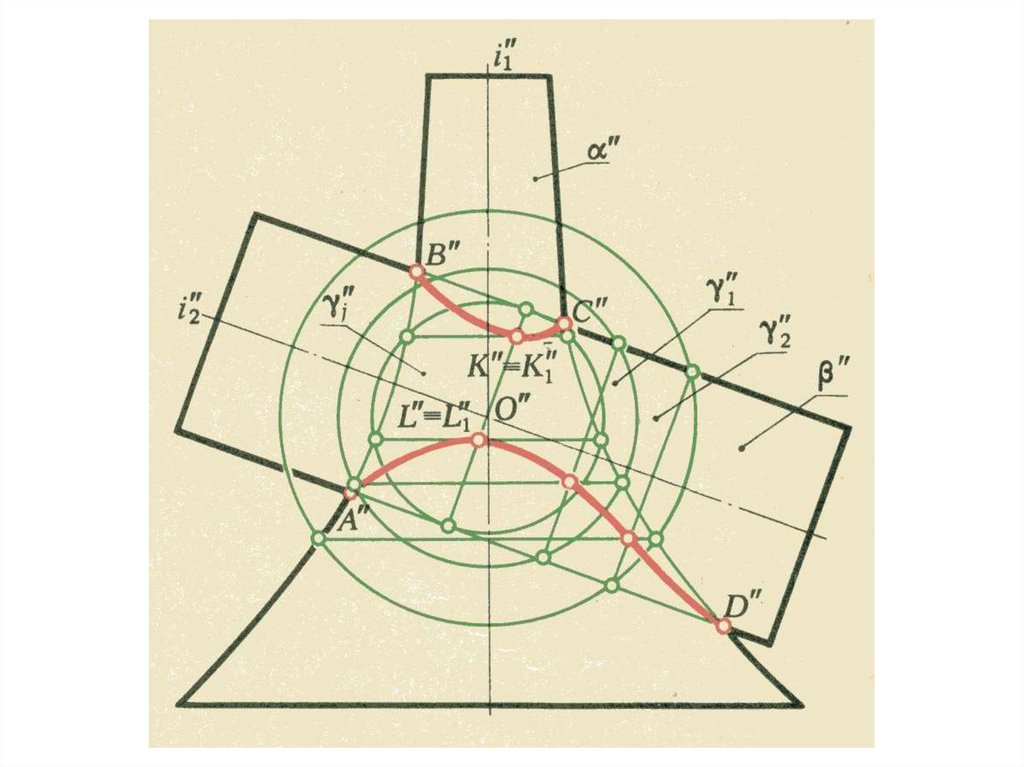
Способ концентрических сферических поверхностей
РМ:рис.53

24.

25.

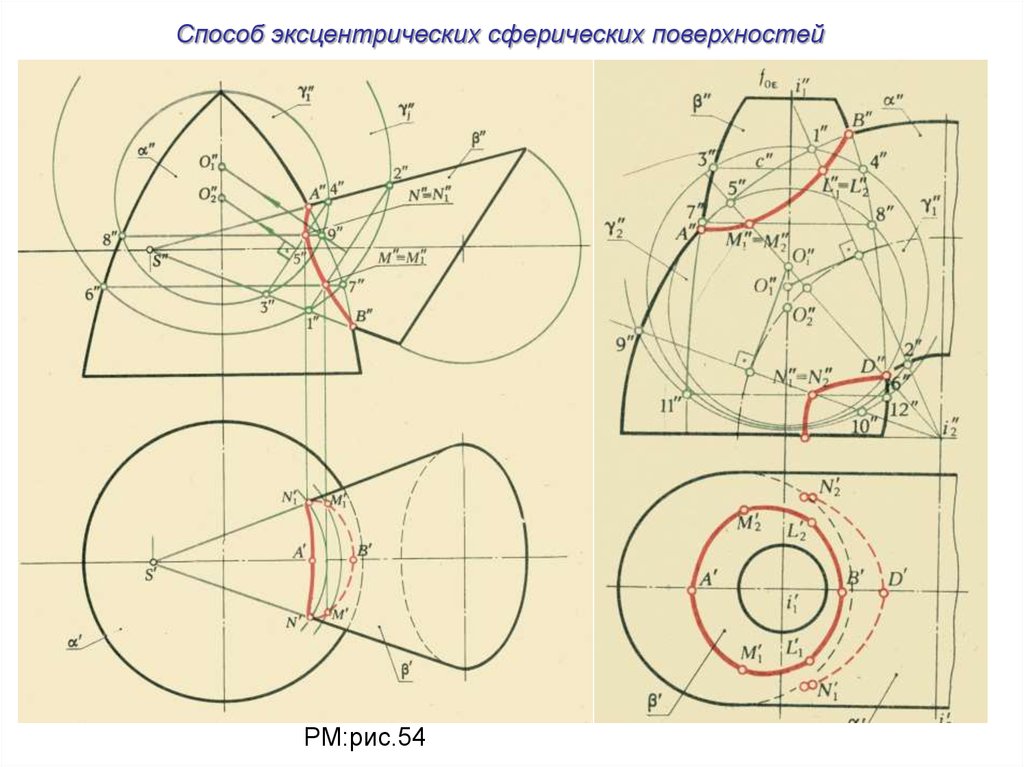
Способ эксцентрических сферических поверхностей
РМ:рис.54

26.

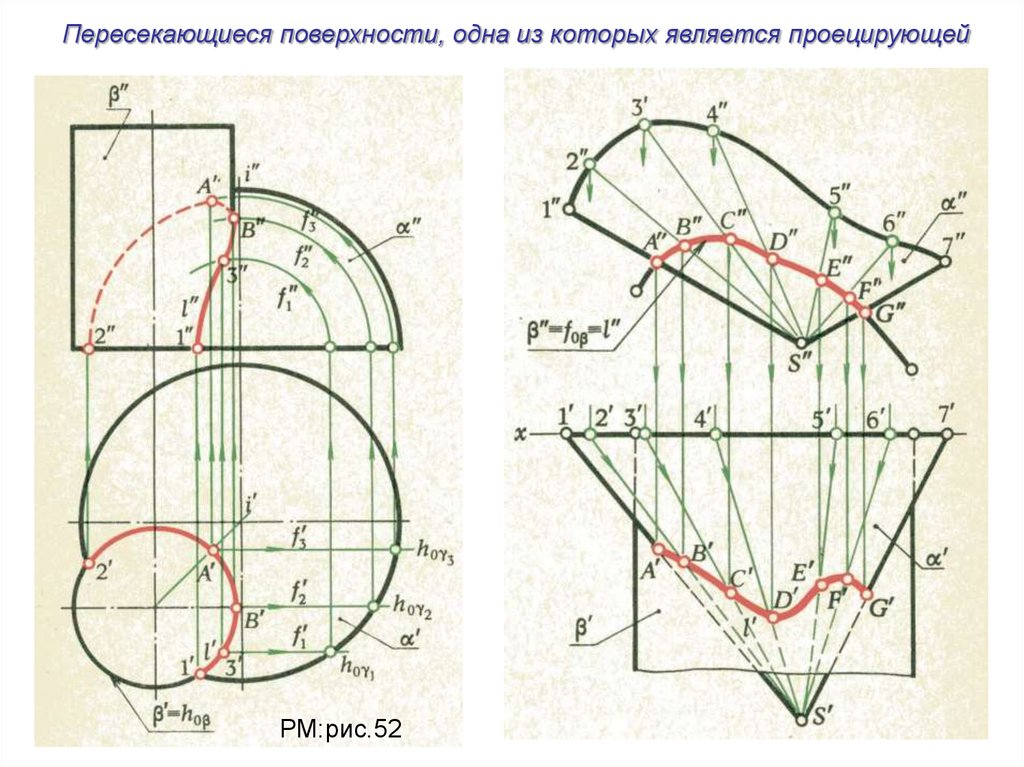
Пересекающиеся поверхности, одна из которых является проецирующей
РМ:рис.52

27.

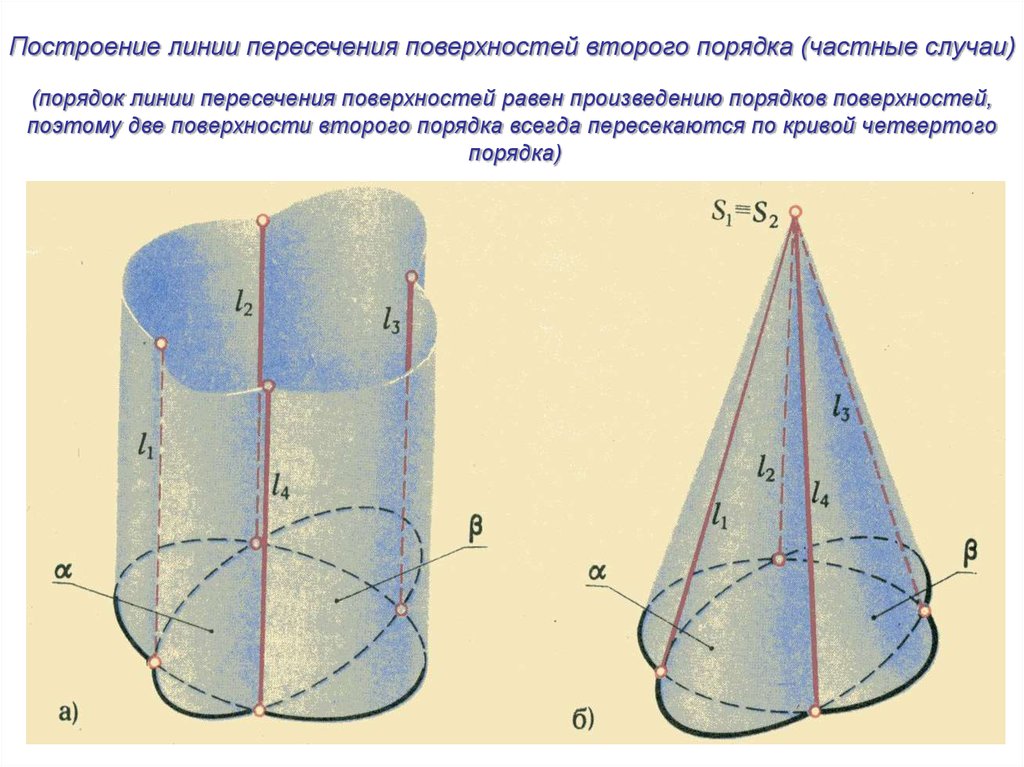
Построение линии пересечения поверхностей второго порядка (частные случаи)
(порядок линии пересечения поверхностей равен произведению порядков поверхностей,
поэтому две поверхности второго порядка всегда пересекаются по кривой четвертого
порядка)

28.

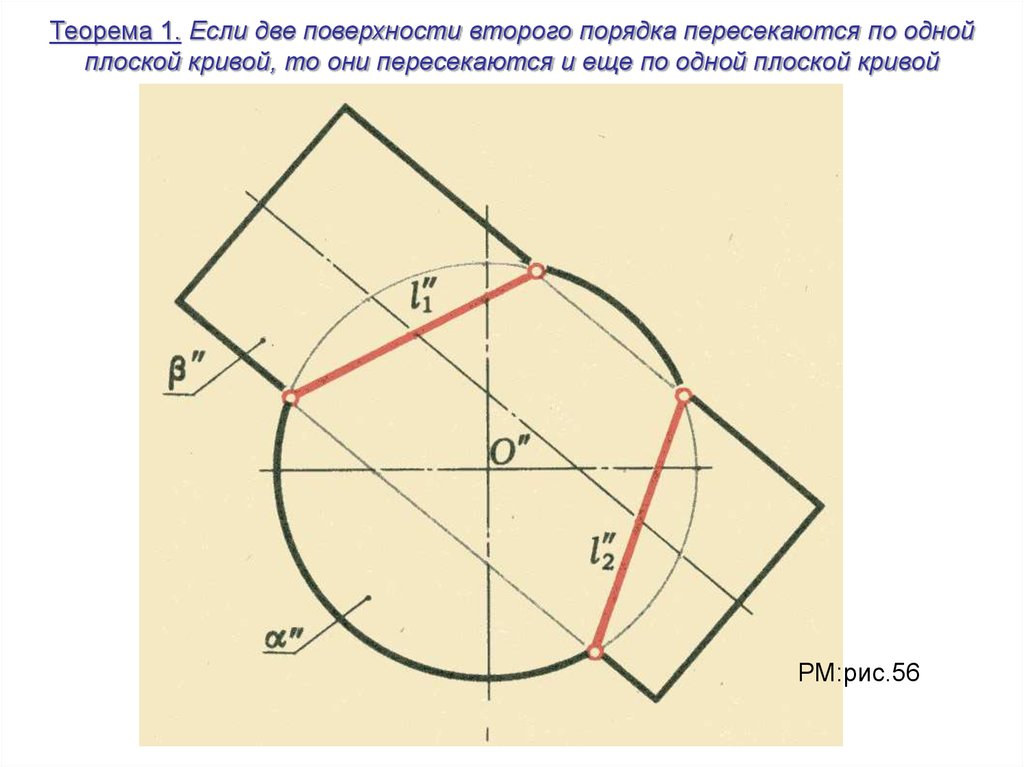
Теорема 1. Если две поверхности второго порядка пересекаются по одной
плоской кривой, то они пересекаются и еще по одной плоской кривой
РМ:рис.56

29.

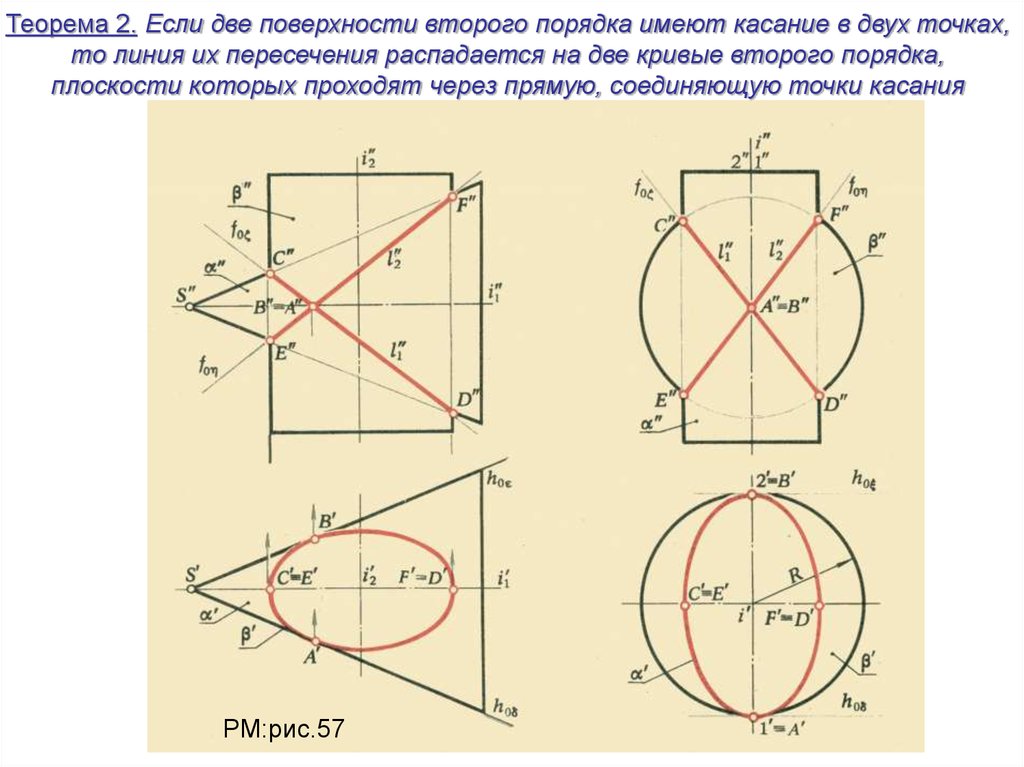
Теорема 2. Если две поверхности второго порядка имеют касание в двух точках,
то линия их пересечения распадается на две кривые второго порядка,
плоскости которых проходят через прямую, соединяющую точки касания
РМ:рис.57

30.

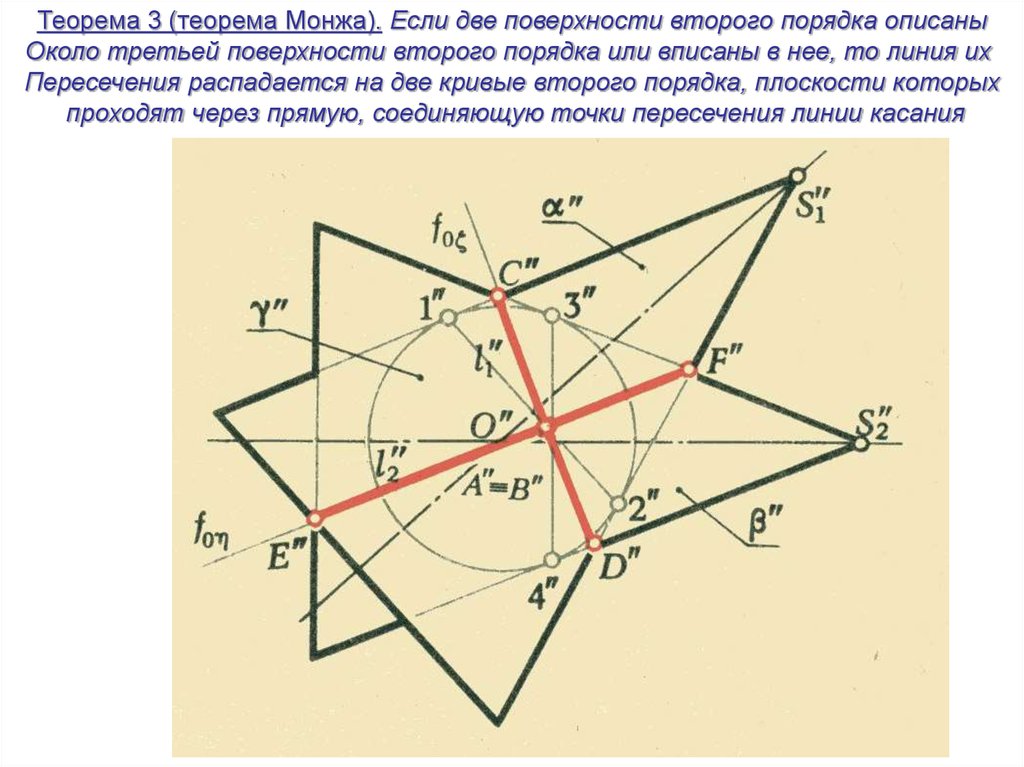
Теорема 3 (теорема Монжа). Если две поверхности второго порядка описаны
Около третьей поверхности второго порядка или вписаны в нее, то линия их
Пересечения распадается на две кривые второго порядка, плоскости которых
проходят через прямую, соединяющую точки пересечения линии касания

31.

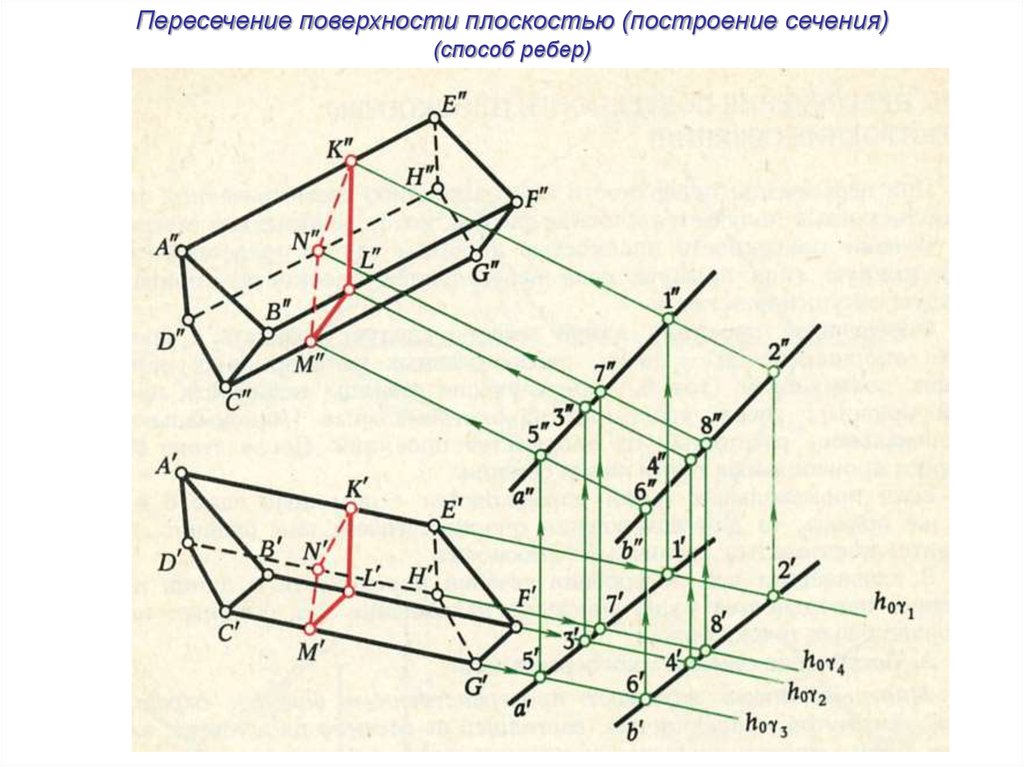
Пересечение поверхности плоскостью (построение сечения)
(способ ребер)

32.

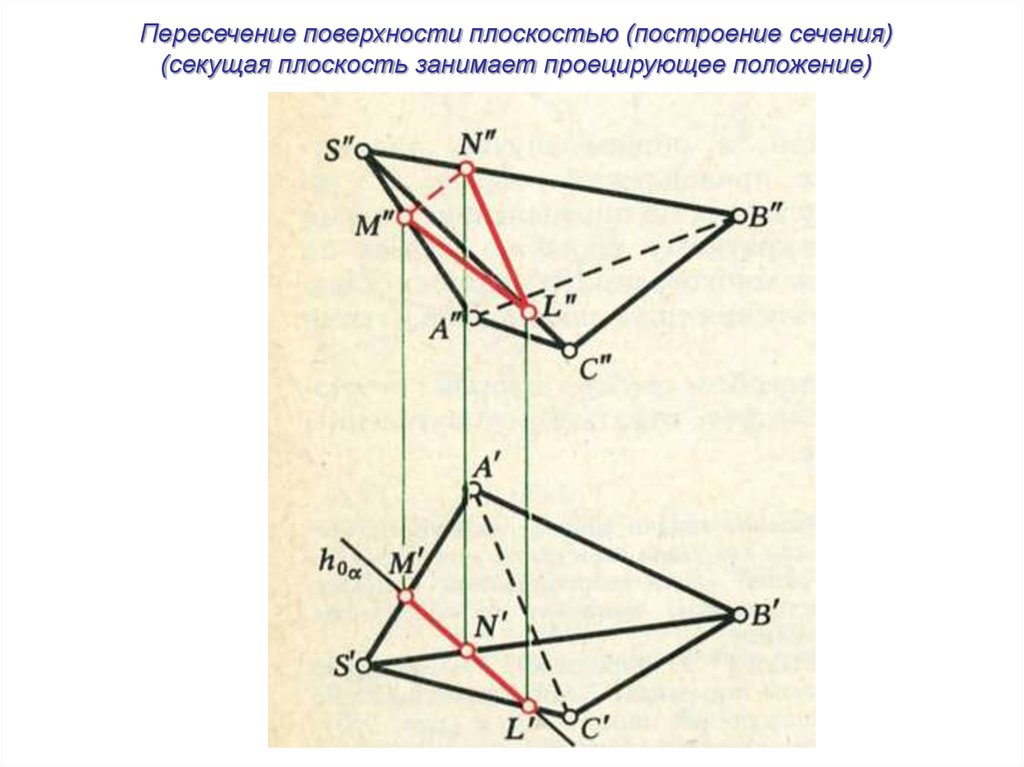
Пересечение поверхности плоскостью (построение сечения)
(секущая плоскость занимает проецирующее положение)

33.

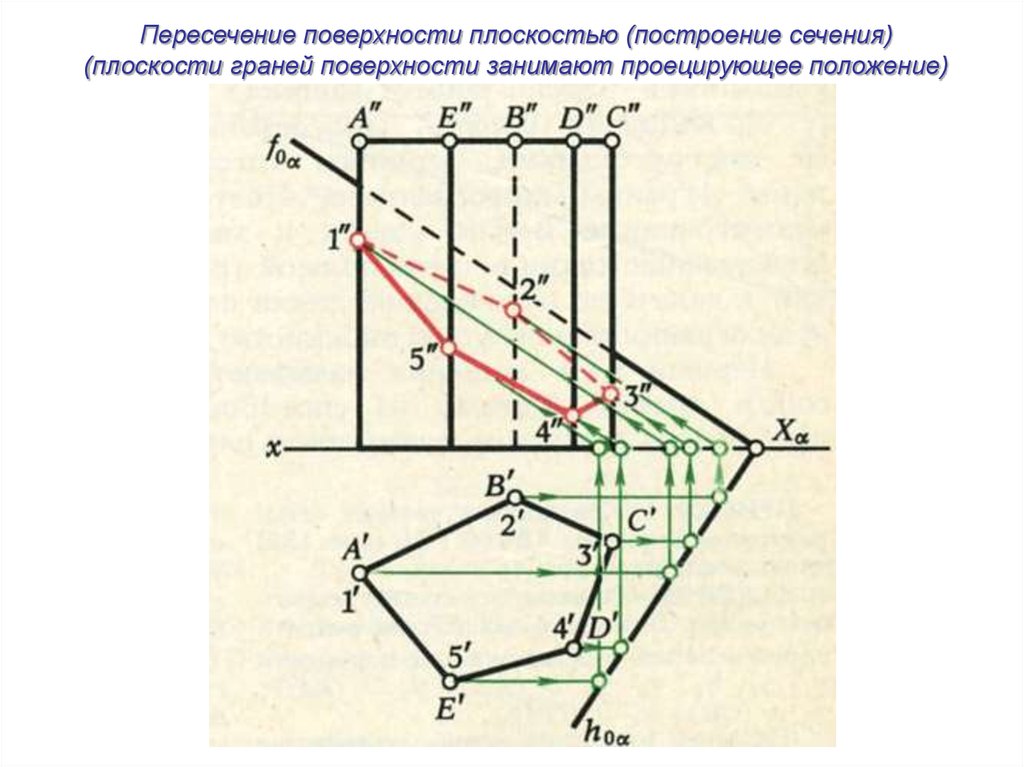
Пересечение поверхности плоскостью (построение сечения)
(плоскости граней поверхности занимают проецирующее положение)

34.

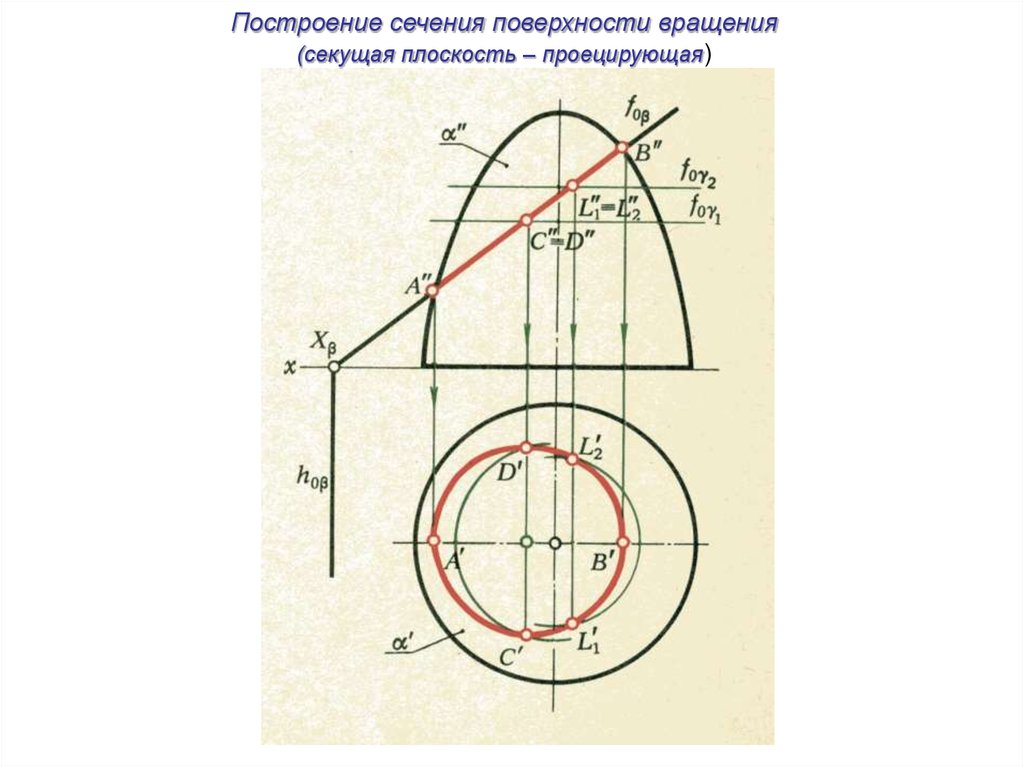
Построение сечения поверхности вращения
(секущая плоскость – проецирующая)

35.

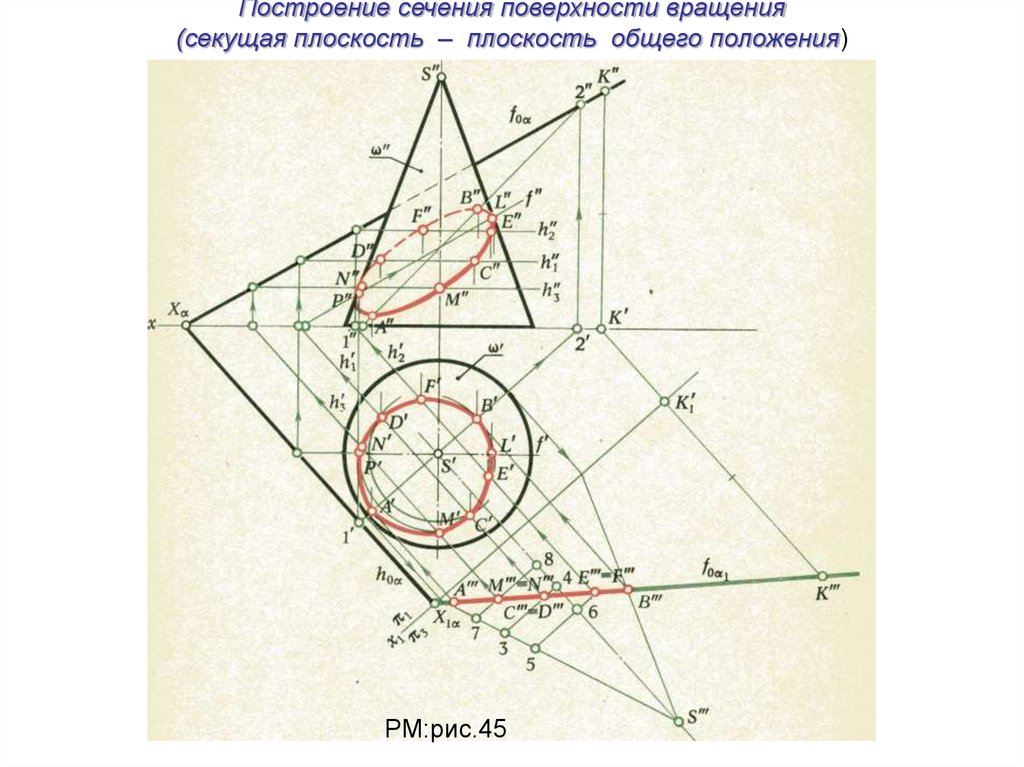
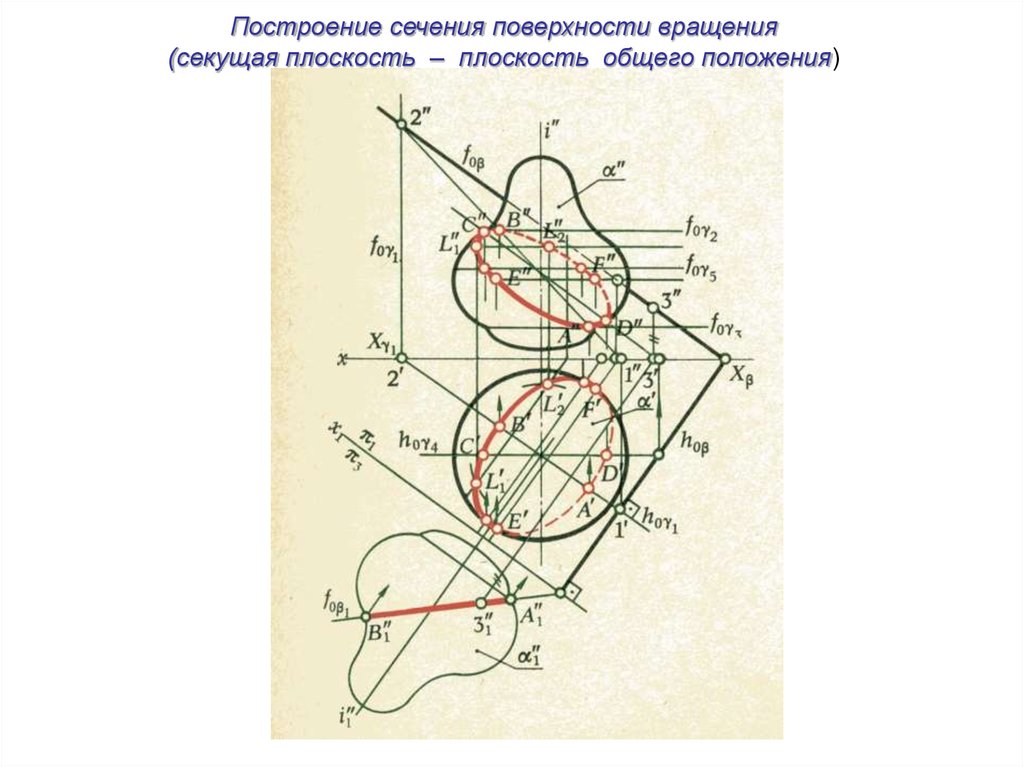
Построение сечения поверхности вращения
(секущая плоскость – плоскость общего положения)
РМ:рис.45

36.

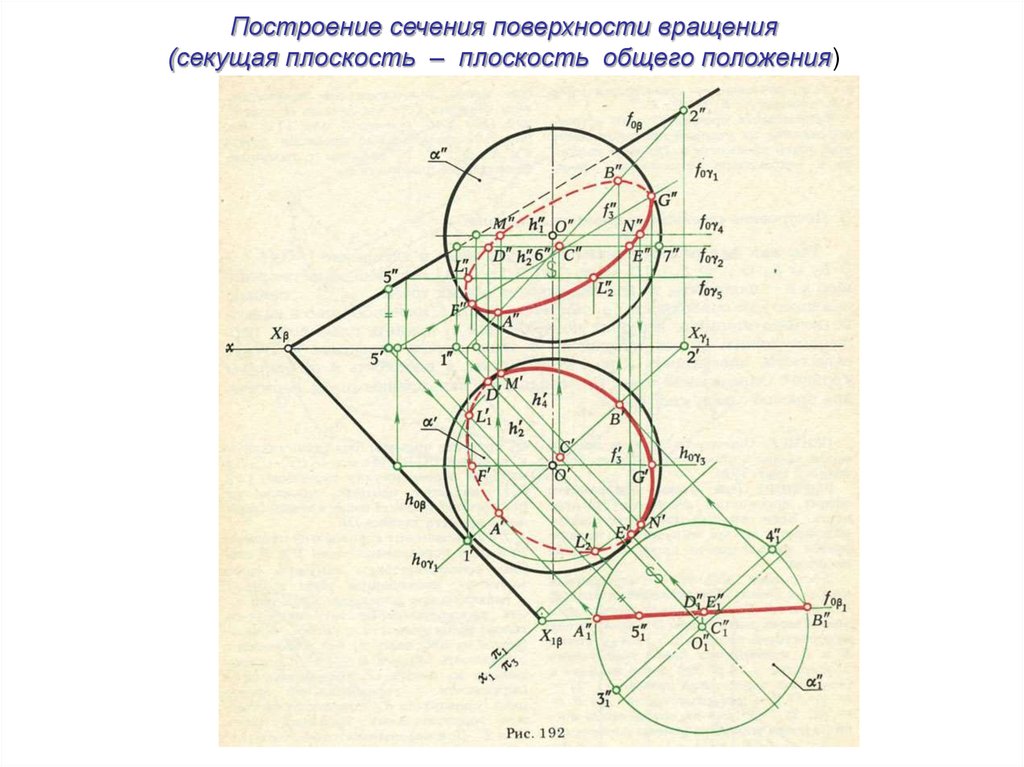
Построение сечения поверхности вращения
(секущая плоскость – плоскость общего положения)

37.

Построение сечения поверхности вращения
(секущая плоскость – плоскость общего положения)

38.

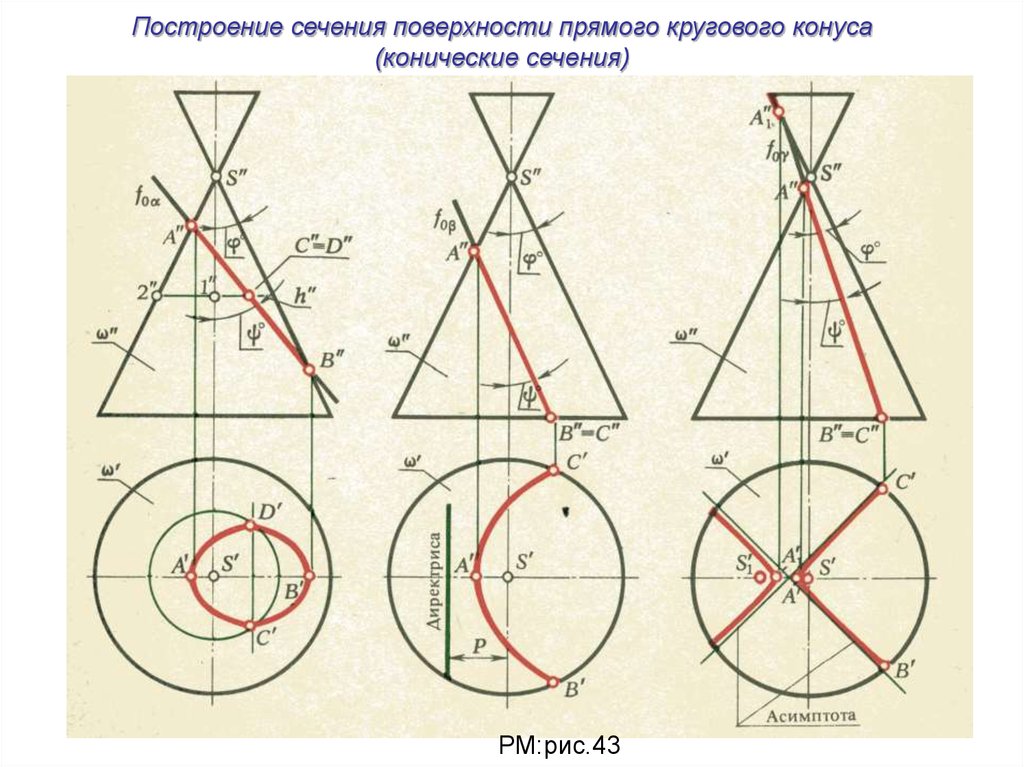
Построение сечения поверхности прямого кругового конуса
(конические сечения)
РМ:рис.43