Транспортная задача

1. ТРАНСПОРТНАЯ ЗАДАЧА

Семинар 1:
ТРАНСПОРТНАЯ ЗАДАЧА
1

2. Постановка задачи

Имеется
m поставщиков A1 , A2, …, Am и n
потребителей B1 , B2, …, Bn некоторого груза.
Для каждого поставщика и потребителя
заданы запасы ai ≥ 0, i = 1, 2, …, m и объем
потребления bj ≥ 0, j = 1, 2, …, n.
Известна стоимость перевозки единицы
груза сij ≥ 0 от i-го поставщика к j-му
потребителю.
Требуется найти объемы всех перевозок xij
от i-го поставщика к j-му потребителю, при
которых общая стоимость минимальна.
2

3. Математическая постановка задачи

Пусть
X = (xij) – m×n матрица, где
xij – объем перевозок от i-го поставщика
к j-му потребителю.
Общие затраты на перевозку груза
определяются функцией:
m
n
z ( X ) cij xij
i 1 j 1
3

4.

Математическая
постановка
транспортной задачи определяется задачей
линейного программирования:
m
n
z ( X ) cij xij min
i 1 j 1
при условиях
m
x
i 1
ij
b j , j 1,..., n
ij
ai , i 1,..., m
n
x
j 1
xij 0
4

5.

Решение
X = (xij) транспортной задачи,
удовлетворяющее условиям и имеющее не
более m+n–1 занятой клетки , будем называть
опорным планом транспортной задачи.
Закрытая модель: суммарные запасы
поставщиков равны суммарным запросам
потребителей, т.е.
m
n
a b
i 1
i
j 1
Открытая
m
модель:
n
a b
i 1
i
j
j 1
j
5

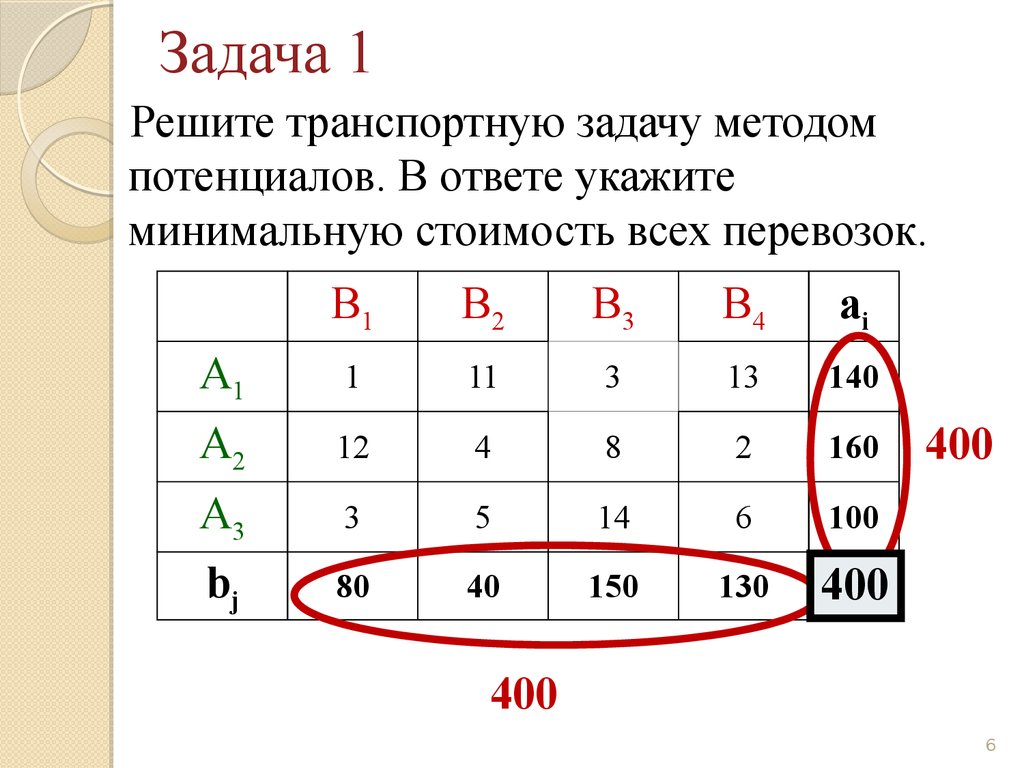
6. Задача 1

Решите транспортную задачу методом
потенциалов. В ответе укажите
минимальную стоимость всех перевозок.
B1
B2
B3
B4
ai
A1
1
11
3
13
140
A2
12
4
8
2
160
A3
3
5
14
6
100
bj
80
40
150
130
400
400
400
6

7.

1. Метод «северо-западного угла»
B1
A1
B2
1
80
11
40
A2
12
A3
3
bj
B3
B4
3
13
8
2
20
4
130
5
30
14
6
100
80
Начальный опорный план:
ai
40
150
130
140
160
100
400
80 40 20 0
X 0 0 130 30
0 0 0 100
z(X) = 1·80 + 11·40 + 3·20 + 8·130 + 2·30 + 6·100 = 2280
7

8.

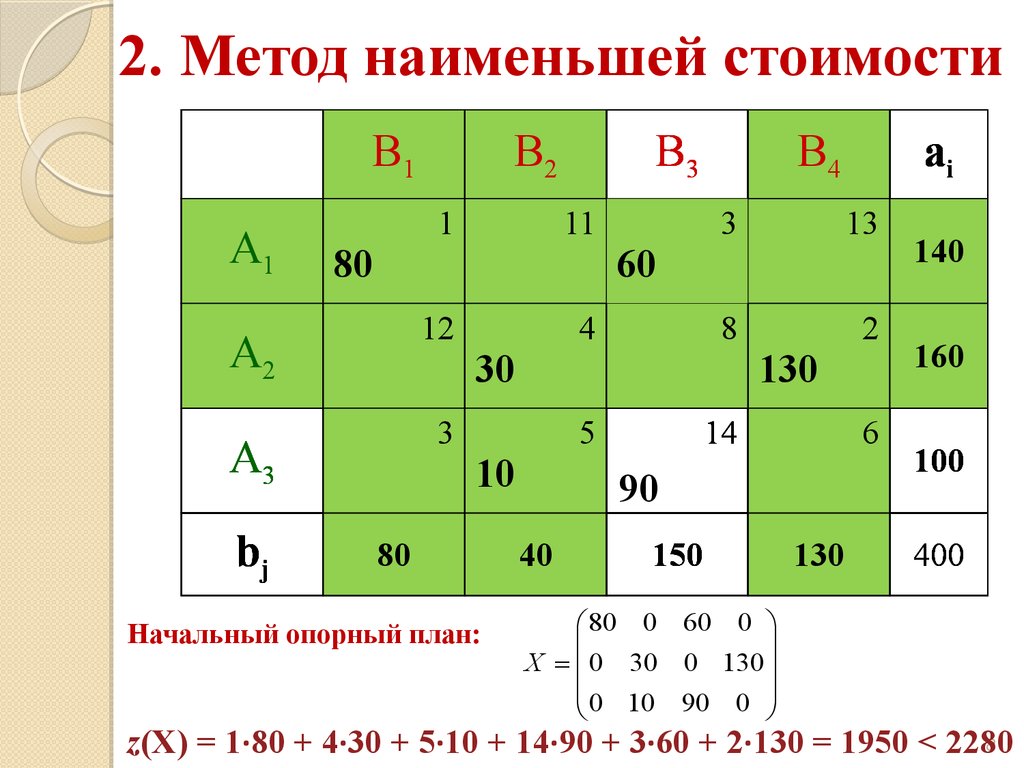
2. Метод наименьшей стоимости
B1
A1
1
B3
11
80
80
B4
ai
3
13
8
2
60
60
12
A2
4
30
30
130
130
3
A3
bj
B2
5
10
10
80
Начальный опорный план:
14
6
90
40
150
80 0 60 0
X 0 30 0 130
0 10 90 0
130
140
160
100
400
8
z(X) = 1·80 + 4·30 + 5·10 + 14·90 + 3·60 + 2·130 = 1950 < 2280

9. Решение транспортной задачи методом потенциалов

Теорема
Если опорный план X = (xij) транспортной
задачи является оптимальным, то существуют
потенциалы поставщиков ui,
i = 1,…, m и потребителей vj, j = 1,…, n,
удовлетворяющие условиям:
ui + vj = сij при xij > 0 (для занятых клеток),
Δij = ui + vj - сij ≤ 0 при xij = 0 (для свободных
клеток).
9

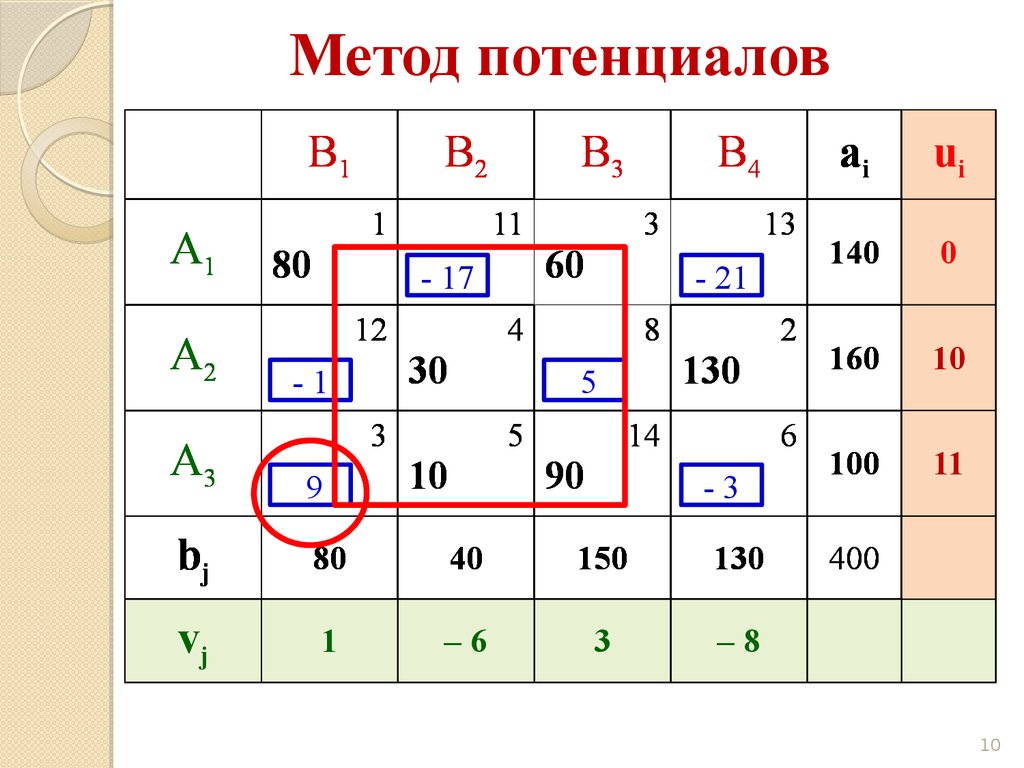
10. Метод потенциалов

B1
A1
A2
B2
1
80
B3
11
12
3
60
- 17
8
5
2
130
5
3
13
- 21
4
30
-1
B4
14
6
A3
9
bj
80
40
150
130
vj
1
–6
3
–8
10
90
-3
ai
ui
140
0
160
10
100
11
400
10

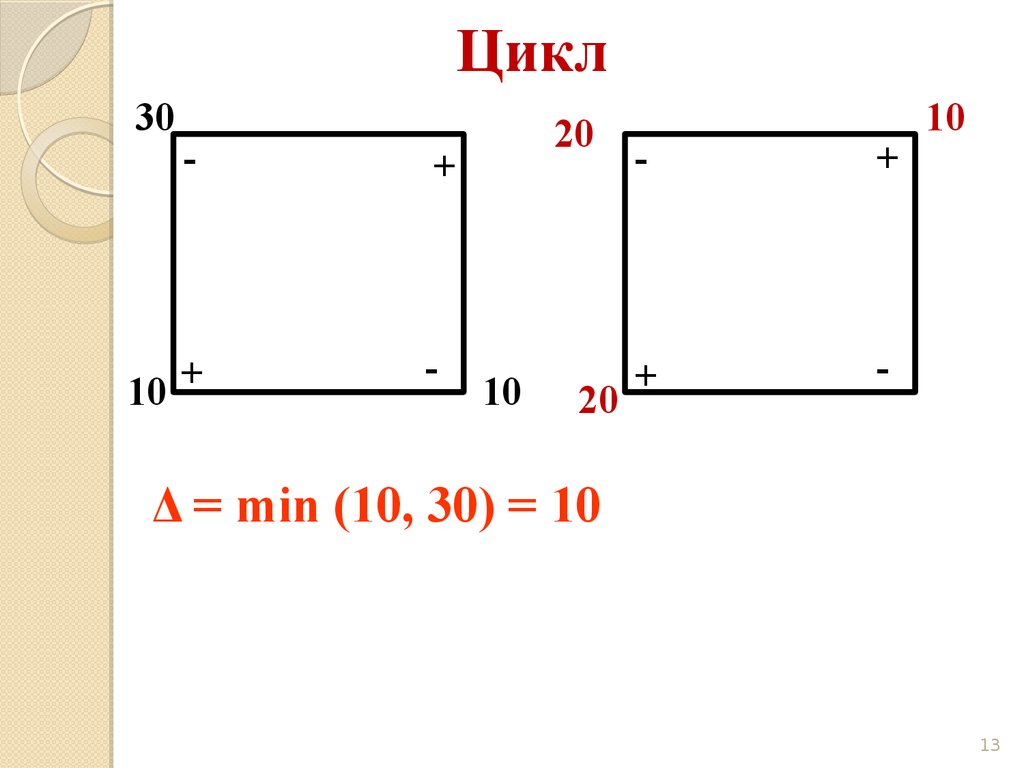
11.

Цикл
80
-
+
+
-
60
90
80
-
+
+
-
140
10
Δ = min (80, 90) = 80
11

12.

Новый опорный план
B1
A1
A2
A3
B2
1
-9
3
140
- 17
8
5
10
2
130
5
3
13
- 21
4
30
- 10
B4
11
12
80
B3
14
10
6
-3
bj
80
40
150
130
vj
3
5
14
3
ai
ui
140
-11
160
-1
100
0
400
z(X) = 3·80 + 5·10 + 4·30 + 14·10 + 3·140 + 2·130 = 1230 <
1950
12

13.

Цикл
30
-
+
10
20
+
-
10
20
-
+
+
-
10
Δ = min (10, 30) = 10
13

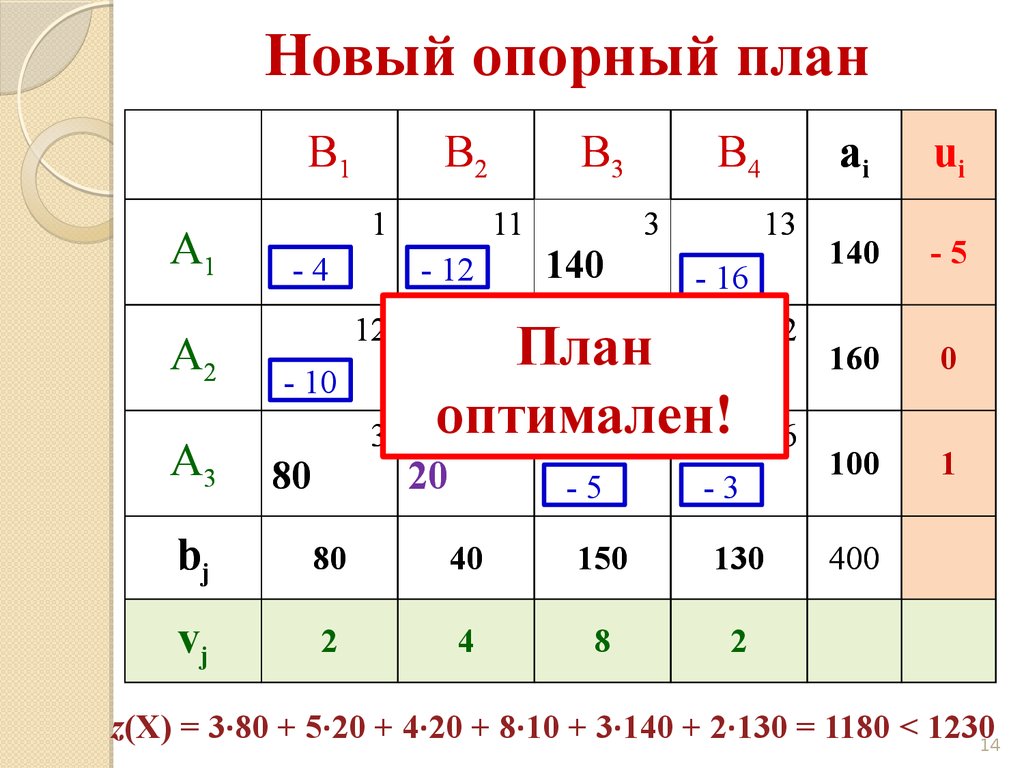
14.

Новый опорный план
B1
A1
A2
A3
B2
1
-4
11
B4
3
140
- 12
12
4
13
- 16
8
План
10
130
оптимален!
5
14
2
20
- 10
3
80
B3
20
-5
-3
bj
80
40
150
130
vj
2
4
8
2
6
ai
ui
140
-5
160
0
100
1
400
z(X) = 3·80 + 5·20 + 4·20 + 8·10 + 3·140 + 2·130 = 1180 < 123014

15. Открытая модель транспортной задачи

Модель
транспортной задачи называется
m
n
открытой, если a b (суммарные
запасы не равны суммарным потребностям).
i 1
i
j 1
j
15

16.

Открытая модель транспортной
задачи
Открытую модель можно свести к закрытой:
1. Если
m
n
i 1
j 1
ai b j
, то вводят фиктивного
потребителя Вn+1 с потребностью
m
n
i 1
j 1
bn 1 ai b j
и нулевыми тарифами перевозок в столбце.
m
n
i 1
j 1
2. Если ai b j ,то вводят фиктивного
поставщика А m+1 с запасом
n
m
j 1
i 1
am 1 b j ai
и
нулевыми тарифами перевозок в строке.
16

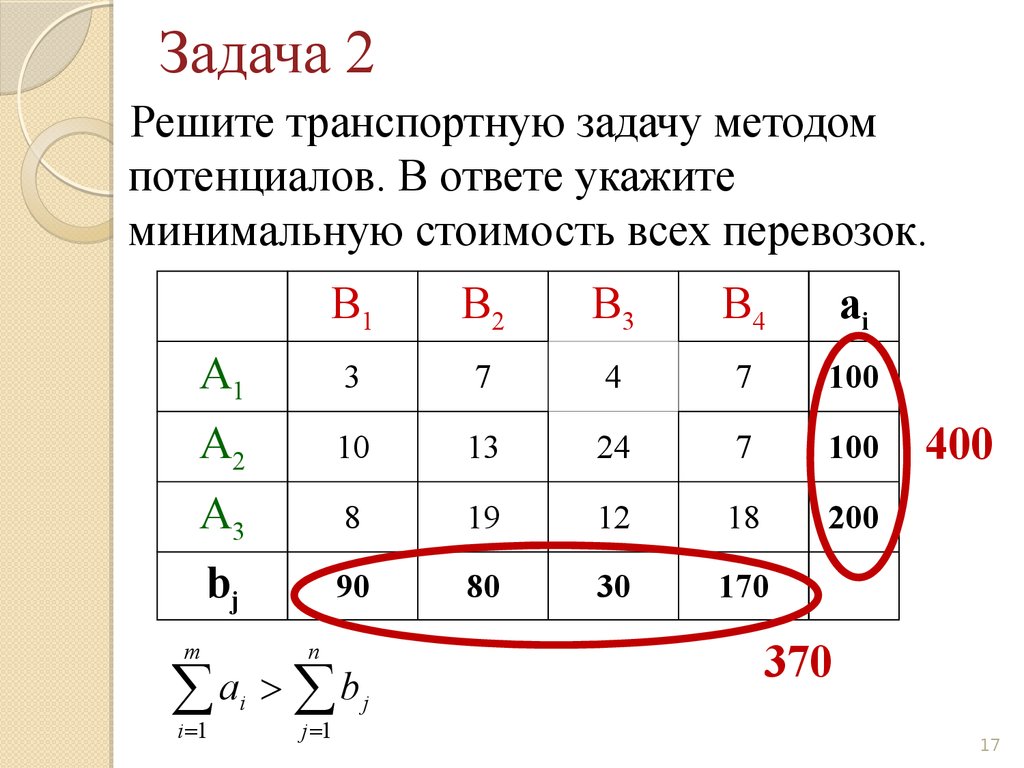
17. Задача 2

Решите транспортную задачу методом
потенциалов. В ответе укажите
минимальную стоимость всех перевозок.
B1
B2
B3
B4
ai
A1
3
7
4
7
100
A2
10
13
24
7
100
A3
8
19
12
18
200
bj
90
80
30
170
m
i 1
370
n
a b
i
j 1
400
j
17

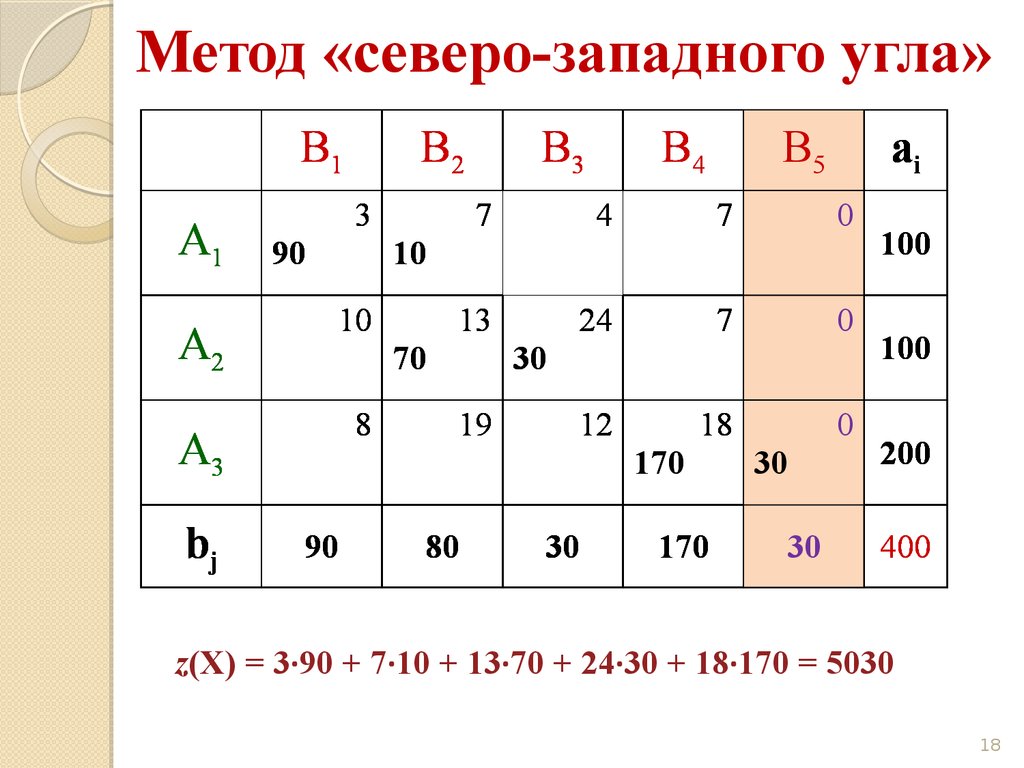
18.

Метод «северо-западного угла»
B1
A1
A2
3
90
B3
B4
B5
ai
7
4
7
0
13
24
7
0
12
18
0
10
10
70
8
A3
bj
B2
30
19
170
90
80
30
170
30
30
100
100
200
400
z(X) = 3·90 + 7·10 + 13·70 + 24·30 + 18·170 = 5030
18

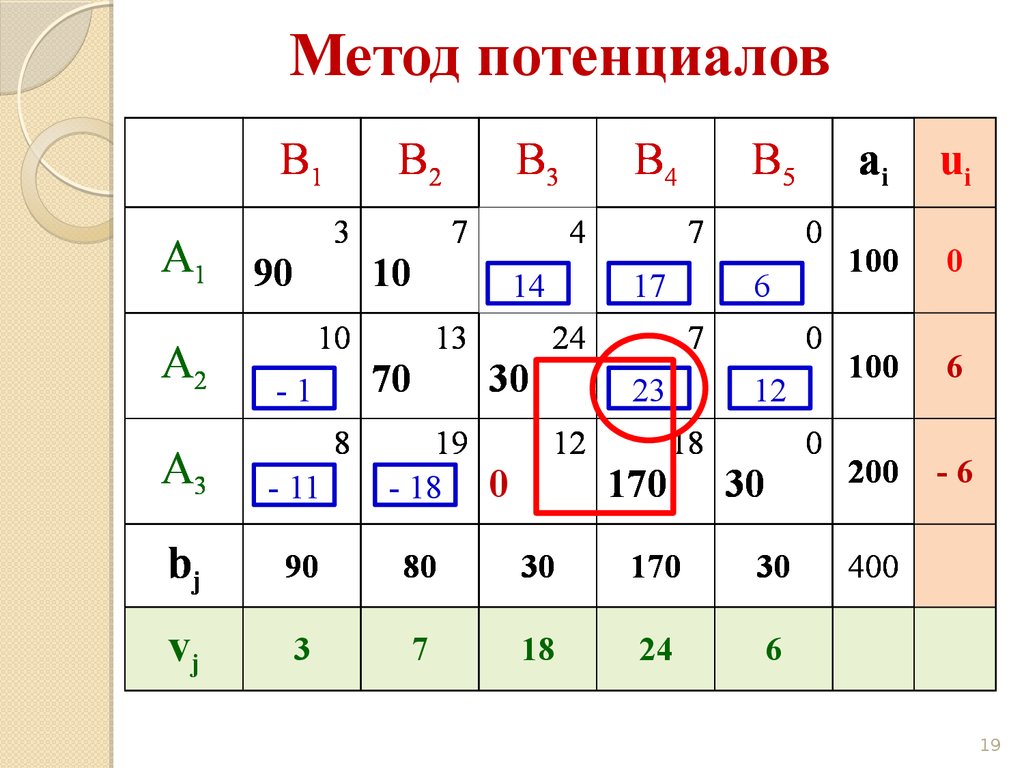
19.

Метод потенциалов
B1
A1
A2
B2
3
90
B3
7
4
10
14
10
13
70
-1
8
B4
7
17
30
0
6
24
19
- 18 0
B5
7
23
12
0
12
18
0
A3
- 11
bj
90
80
30
170
30
vj
3
7
18
24
6
170
30
ai
ui
100
0
100
6
200
-6
400
19

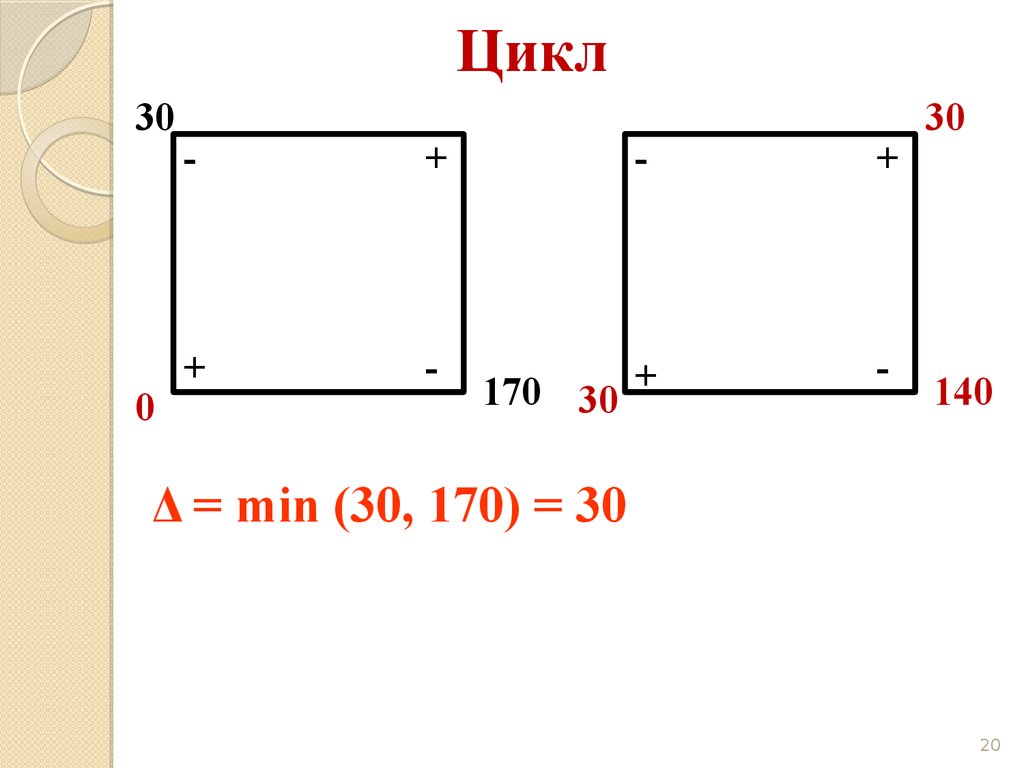
20.

Цикл
30
0
-
+
-
+
+
-
+
-
170 30
30
140
Δ = min (30, 170) = 30
20

21.

Новый опорный план
B1
A1
A2
B2
3
90
B3
7
10
10
4
-9
13
70
-1
8
B4
7
-6
- 23
0
7
30
12
0
- 11
18
0
A3
12
5
bj
90
80
30
170
30
vj
20
24
12
18
0
30
ai
- 17
24
19
B5
140
30
ui
100 -17
100
-11
200
0
400
z(X) = 3·90 + 7·10 + 13·70 + 7·30 + 18·140 + 12·30 = 4130 < 5030
21

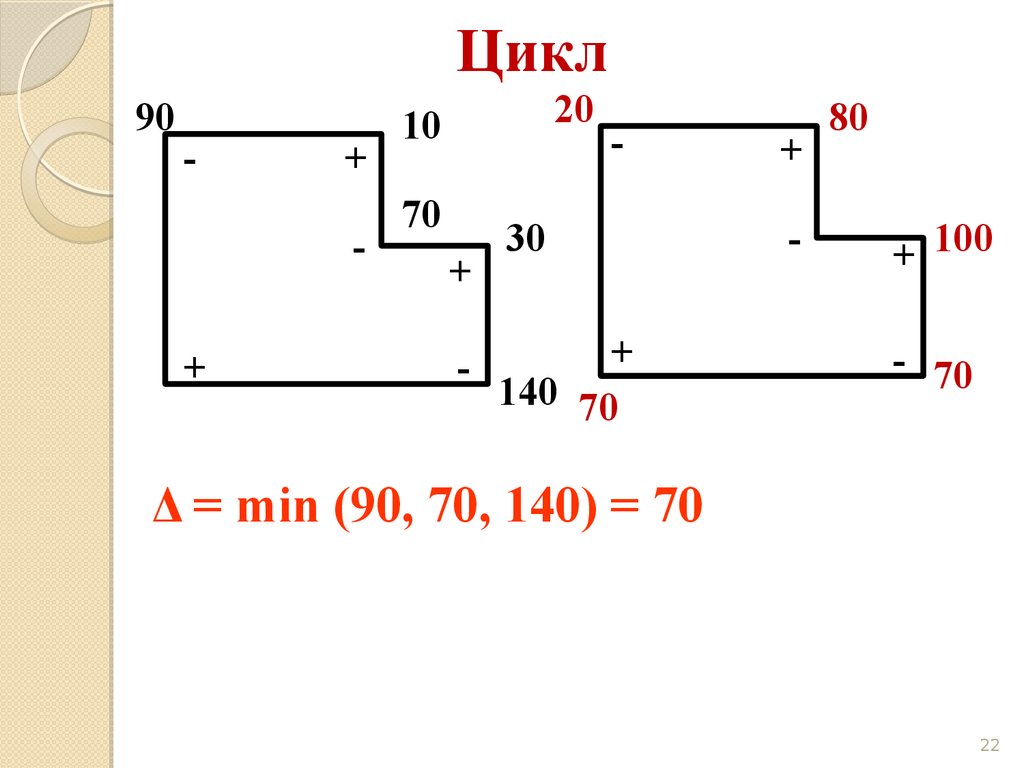
22.

Цикл
90
-
+
-
+
20
10
70
+
-
-
30
+
140 70
+
-
80
+ 100
- 70
Δ = min (90, 70, 140) = 70
22

23.

Новый опорный план
B1
A1
A2
A3
B2
3
20
B3
7
80
10
- 13
70
4
3
13
- 12
8
B4
-7
7
6
- 23
7
100
12
30
0
-5
24
19
B5
0
- 11
18
70
0
30
bj
90
80
30
170
30
vj
8
12
12
18
0
ai
ui
100
-5
100 -11
200
0
400
z(X) = 3·20 + 7·80 + 8·70 + 12·30 + 18·70 + 7·100 = 3500 < 4130
23

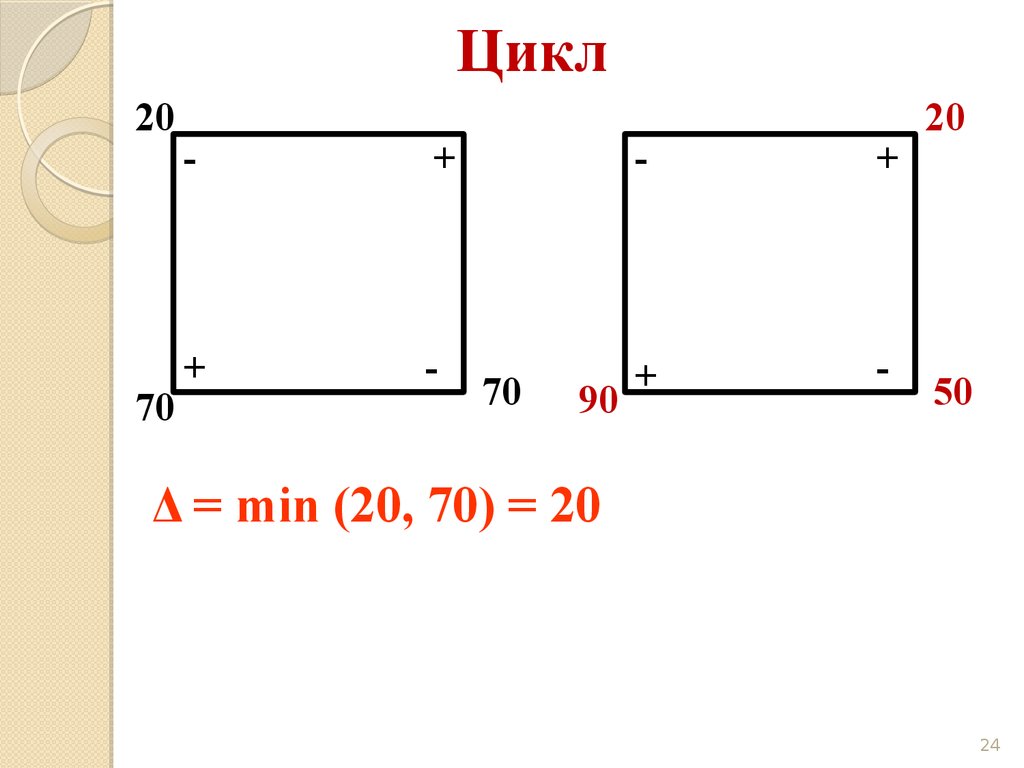
24.

Цикл
20
70
-
+
-
+
+
-
+
-
70
90
20
50
Δ = min (20, 70) = 20
24

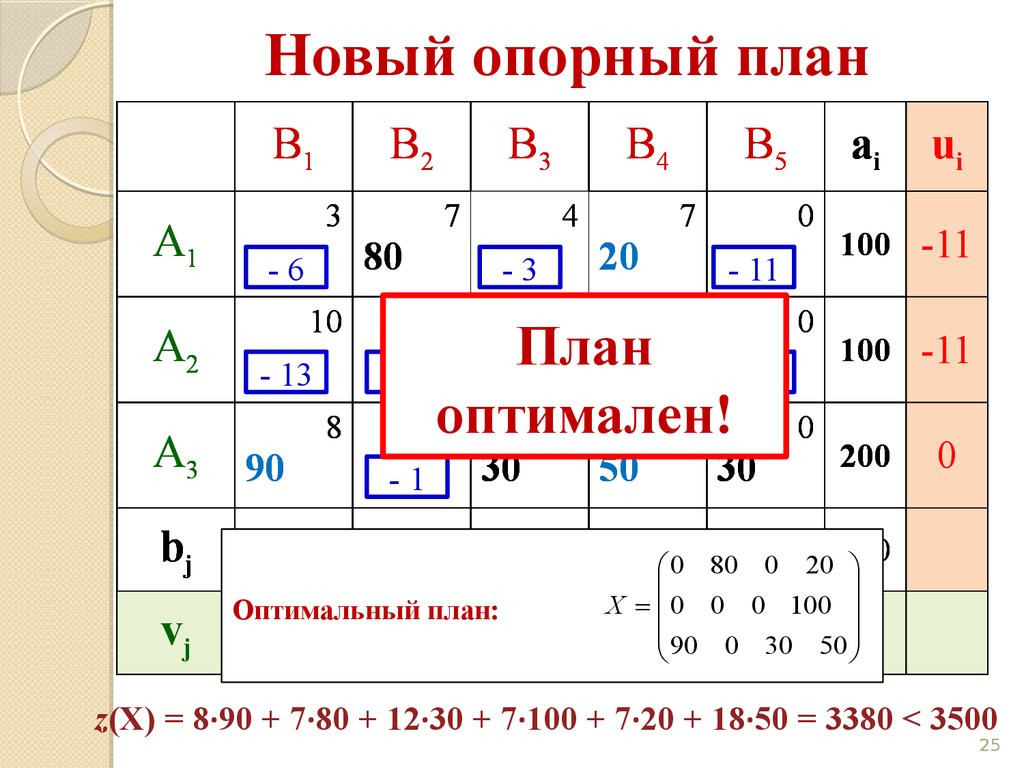
25.

Новый опорный план
B1
A1
A2
A3
bj
vj
B2
3
B3
7
4
80
-6
10
- 13
8
90
13
7
24
30
80
18
30
12
ai
0
- 11
7
План
100
-6
- 23
- 11
оптимален!
19
12
18
Оптимальный план:
8
B5
20
-3
-1
90
B4
50
30
0
0
ui
100 -11
100 -11
200
0
170 0
80 30
0 20 400
X 0 0 0 100
18 90 0 030 50
z(X) = 8·90 + 7·80 + 12·30 + 7·100 + 7·20 + 18·50 = 3380 < 3500
25

26. Задача 3

Решите транспортную задачу методом
потенциалов. В ответе укажите
минимальную стоимость всех перевозок.
B1
B2
B3
B4
ai
A1
1
13
12
3
60
A2
2
16
4
6
125
A3
13
4
17
16
75
bj
100
100
50
50
m
i 1
300
n
a b
i
j 1
260
j
26

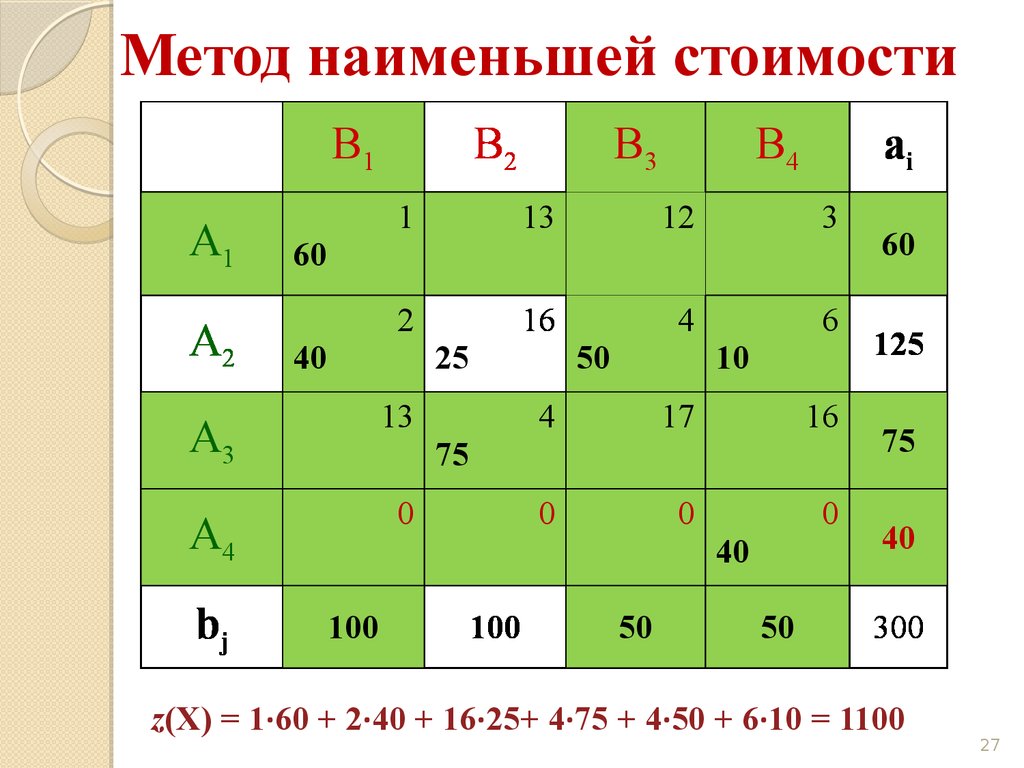
27.

Метод наименьшей стоимости
B1
A1
A2
B2
B4
ai
1
13
12
3
2
16
4
6
60
40
25
A3
13
A4
0
bj
B3
50
10
4
17
16
0
0
0
75
40
100
100
50
50
60
125
75
40
300
z(X) = 1·60 + 2·40 + 16·25+ 4·75 + 4·50 + 6·10 = 1100
27

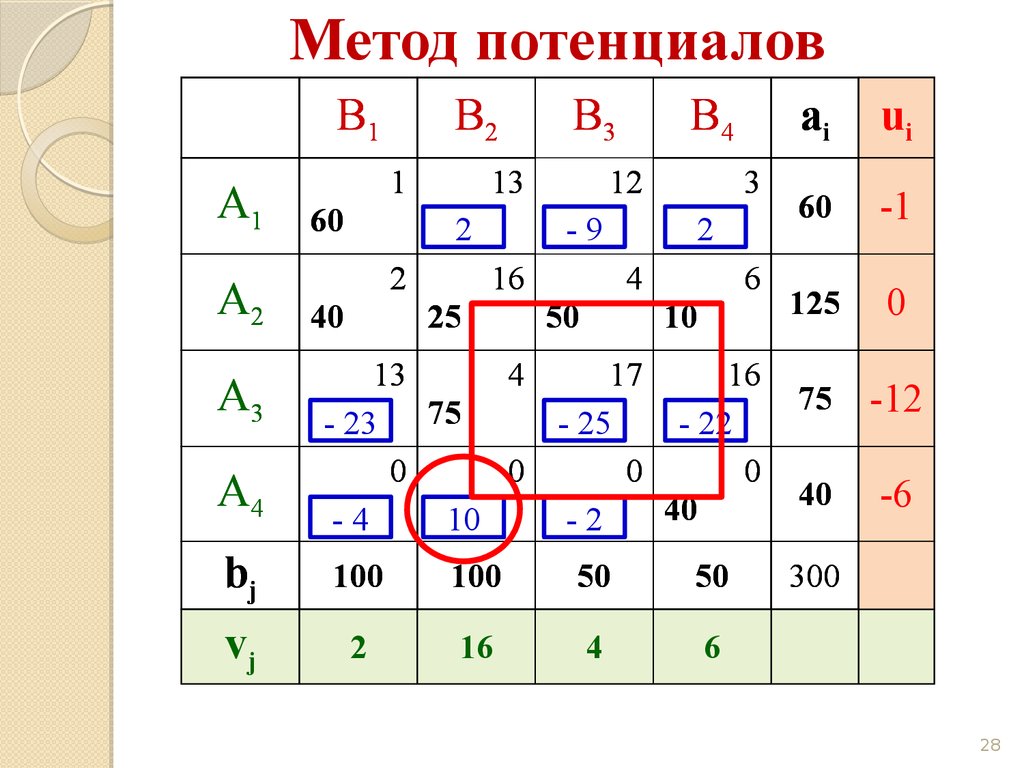
28.

Метод потенциалов
B1
A1
A2
B2
1
60
13
2
2
40
B3
B4
12
-9
16
25
3
2
4
50
6
10
A4
13
4
17
16
- 23 75
- 25
- 22
0
0
0
0
40
-4
10
-2
bj
100
100
50
50
vj
2
16
4
6
A3
ai
ui
60
-1
125
0
75
-12
40
-6
300
28

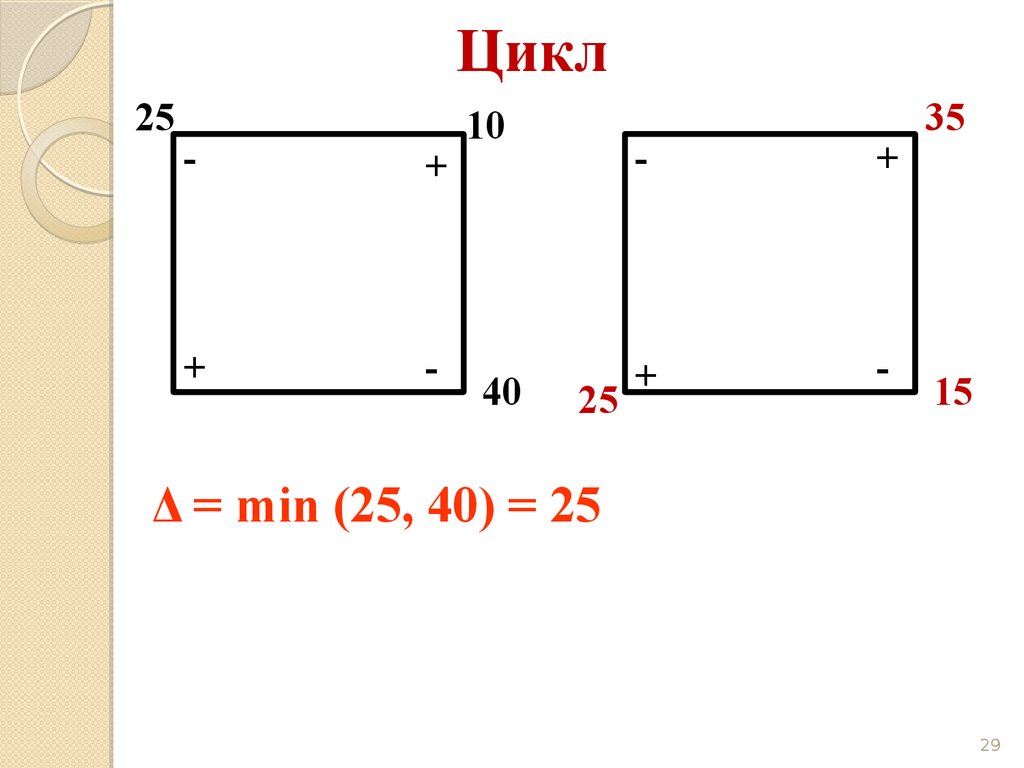
29.

Цикл
25
-
+
+
-
10
40
25
-
+
+
-
35
15
Δ = min (25, 40) = 25
29

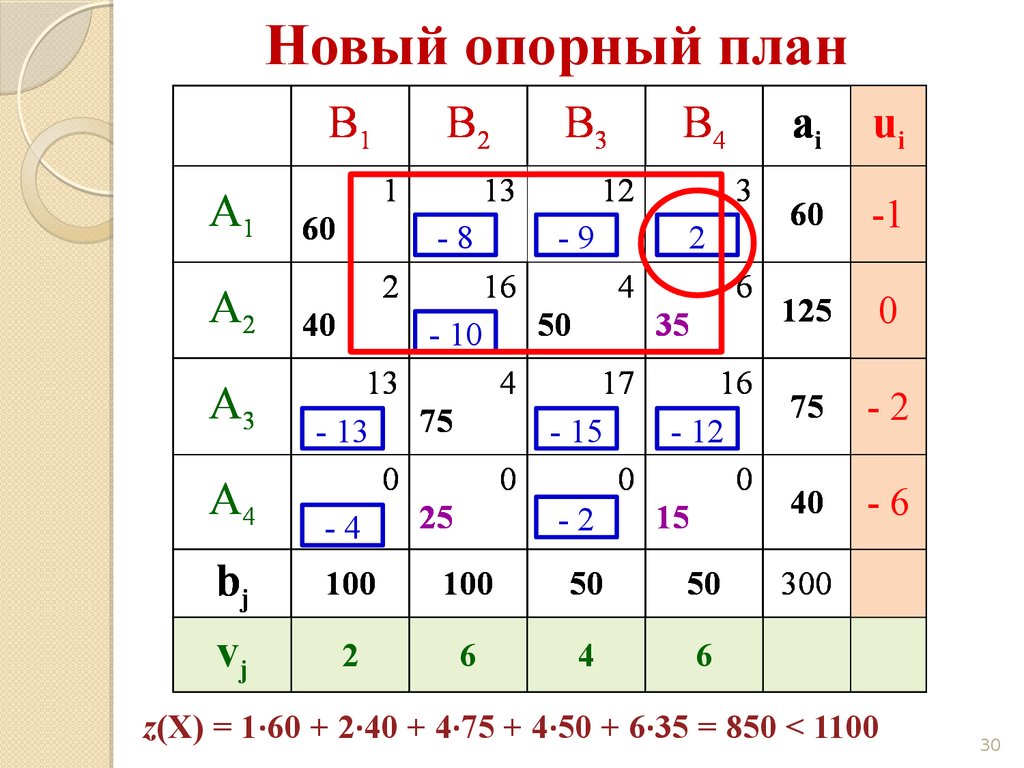
30.

Новый опорный план
B1
A1
A2
B2
1
60
B3
13
-8
2
40
B4
12
-9
16
2
4
50
- 10
3
6
35
A4
13
- 13 75
0
25
-4
bj
100
100
50
50
vj
2
6
4
6
A3
4
17
16
- 15
- 12
0
0
0
15
-2
ai
ui
60
-1
125
0
75
-2
40
-6
300
z(X) = 1·60 + 2·40 + 4·75 + 4·50 + 6·35 = 850 < 1100
30

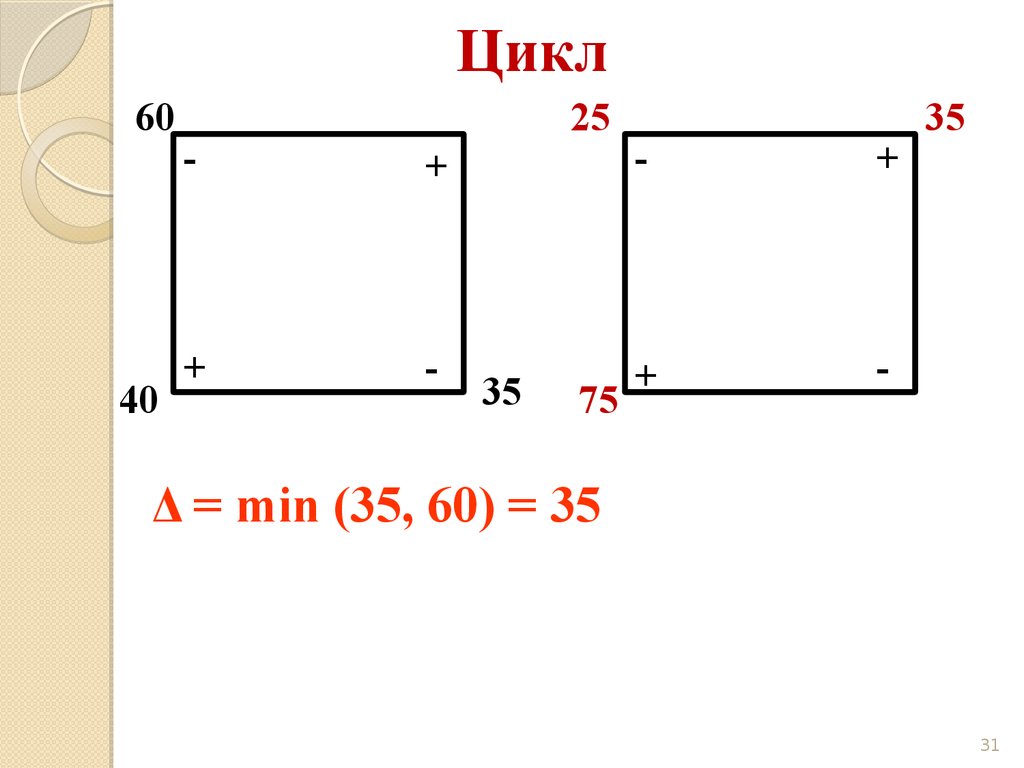
31.

Цикл
60
40
25
-
+
-
+
+
-
+
-
35
75
35
Δ = min (35, 60) = 35
31

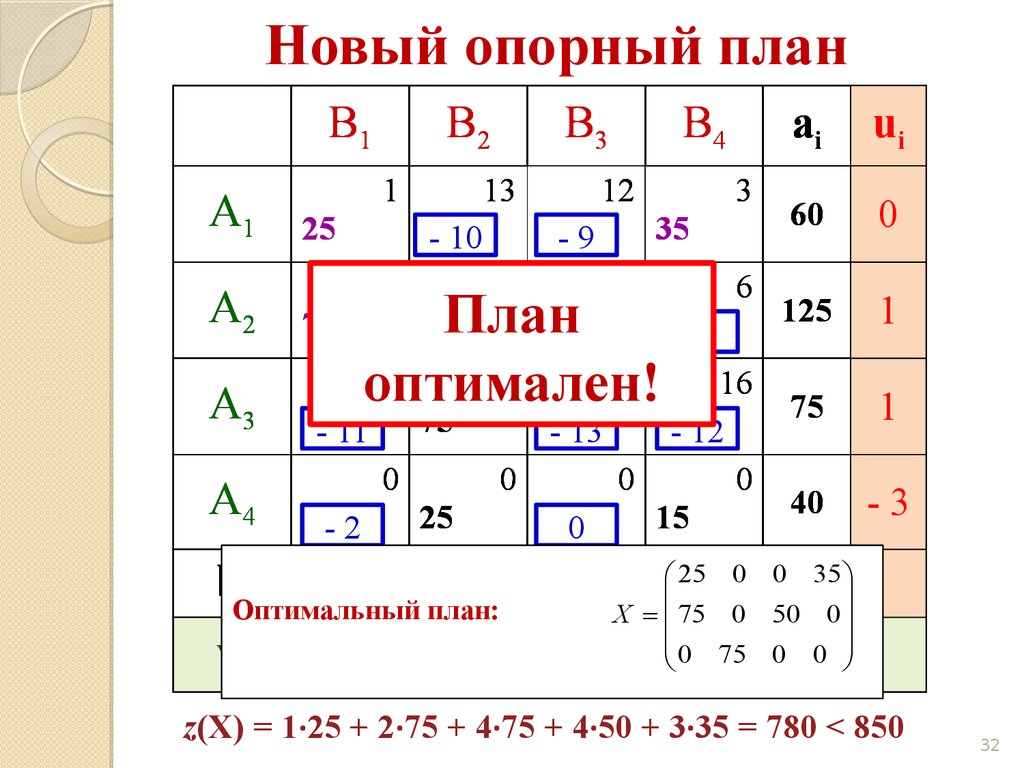
32.

Новый опорный план
B1
A1
A2
A3
B2
1
25
B3
13
- 10
2
B4
12
35
-9
16
3
4
50
- План
12
13
4
17
оптимален!
75
-2
16
- 13
- 12
0
0
0
15
0
75
- 11
6
0
A4
-2
bj
100
100
50
vj
1
3
3
25
Оптимальный план:
ai
ui
60
0
125
1
75
1
40
-3
0 0300
35
25
50
X 75 0 50 0
0 3 75 0 0
z(X) = 1·25 + 2·75 + 4·75 + 4·50 + 3·35 = 780 < 850
32

33.

Транспортные задачи с
дополнительными ограничениями
В
некоторых транспортных задачах
наложены дополнительные ограничения на
перевозку грузов.
1. Если в закрытой задаче перевозки от
поставщика Ai к потребителю Bj не могут
быть осуществлены (стоит блокировка),
для определения оптимального решения
задач предполагают, что тариф перевозки
единицы груза равен сколь угодно
большому числу М.
33

34.

2. Если дополнительным условием в задаче является
обеспечение перевозки от поставщика Ai к
потребителю Bj в точности aij единиц груза, в
клетку AiBj записывают указанное число aij, а эту
клетку считают свободной со сколь угодно
большим тарифом М.
3. Если от поставщика Ai к потребителю Bj должно
быть перевезено не менее aij единиц груза, то
запасы пункта Ai и потребности Bj полагают
меньше фактических на aij единиц. После
нахождения оптимального плана перевозку в
клетке AiBj увеличивают на aij единиц.
34

35.

4. Если от поставщика Ai к потребителю Bj
требуется перевезти не более aij единиц
груза, то вводят дополнительного
потребителя Bn+1 = Bij, которому
записывают те же тарифы, что и для Bj, за
исключением тарифа в i–й строке, который
считают равным сколь угодно большому
числу М.
Потребности пункта Bj считают равными
aij, а потребности Bij полагают равными
bj - aij.
35

36. Спасибо за внимание!

36