Похожие презентации:
Динамика материальной точки
1. Динамика материальной точки
законы Ньютонамасса, сила, импульс, центр масс
система единиц
закон сохранения импульса
закон движения центра масс
2. И.Ньютон – основоположник классической механики
«Математические началанатуральной философии»
1687г.
1. Сформулировал
основные
законы классической механики
И.Ньютон
1643-1727
2.Создал
физическую
картину
мира
(ньютоновская
теория
абсолютного
пространства
и
времени)
3. Первый закон классической механики
Всякое тело остаетсяв состоянии покоя
или прямолинейного
равномерного
движения, пока
внешние
взаимодействия не
выведут его из этого
состояния
(формулировка
Ньютона)
Существуют такие
системы отсчета,
называемые
инерциальными, в
которых
материальная точка,
на которую не
действуют другие
тела, движется
прямолинейно
равномерно или
покоится
4. Инертность
I закон - обобщение закона инерции (1609, Г. Галилей)Фундаментальное свойство
тел сохранять состояние
покоя или прямолинейного
равномерного
движения
называется инертностью
Г.Галилей
1564-1642
Физическая величина,
характеризующая
инертность тела,
называется инертной
массой.
5. Динамические характеристики
Сила – векторная величина, являющаяся мероймеханического воздействия на тело со стороны
других тел или полей, в результате которого тело
получает ускорение или изменяет свою форму и
размеры.
Масса – физическая величина, характеризующая
свойство инертности тела.
Импульс - векторная величина численно равная
произведению массы материальной точки на ее
скорость.
p m
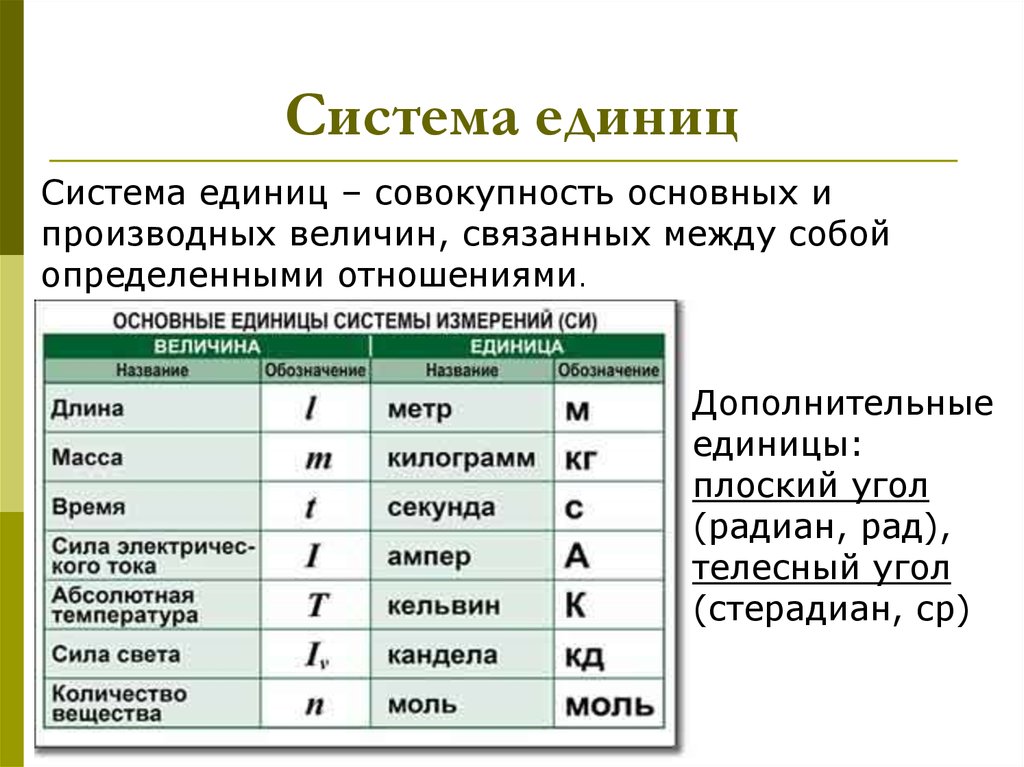
6. Система единиц
Система единиц – совокупность основных ипроизводных величин, связанных между собой
определенными отношениями.
Дополнительные
единицы:
плоский угол
(радиан, рад),
телесный угол
(стерадиан, ср)
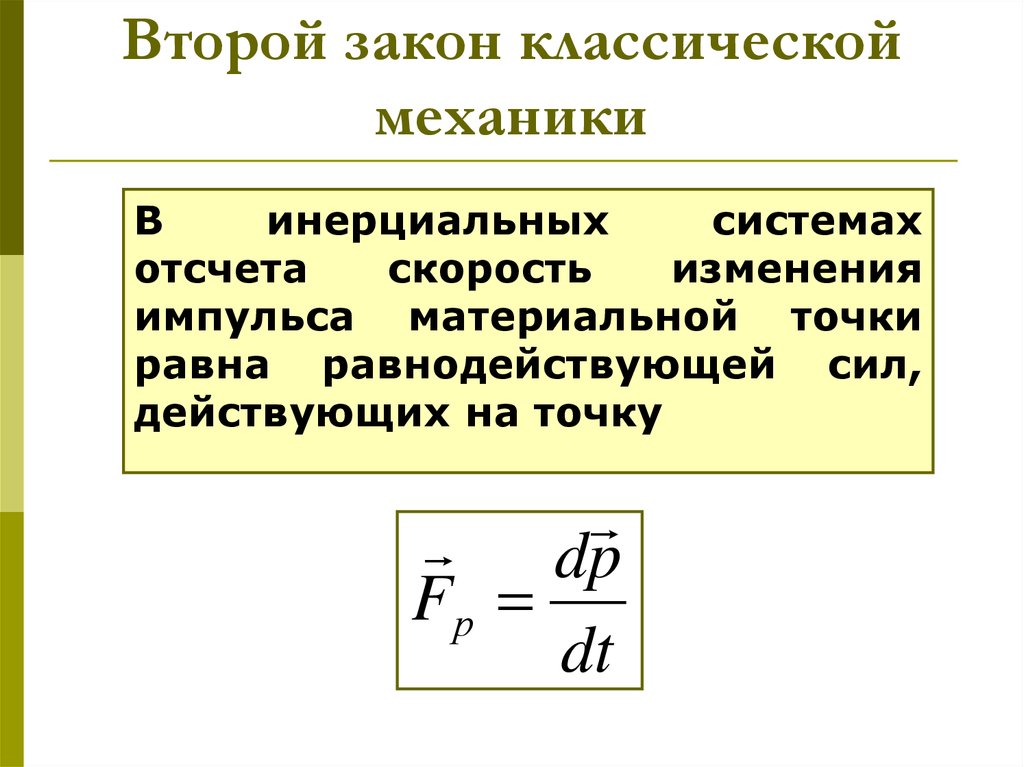
7. Второй закон классической механики
Винерциальных
системах
отсчета
скорость
изменения
импульса материальной точки
равна равнодействующей сил,
действующих на точку
dp
Fр
dt
8. Замечания
• II закон является определением силы какпроизводной импульса материальной точки
по времени
• II закон определяет единицу измерения
силы
• II закон- динамическое уравнение движения
материальной точки
• II
закон
связывает
динамические
кинематические характеристики движения
и
9. Следствие второго закона Ньютона
dmdp d
d
FР
m
m
dt dt
dt
dt
В
инерциальной
системе
отсчета
ускорение, приобретаемое телом, прямо
пропорционально равнодействующей сил,
действующих на данное тело, и обратно
пропорционально массе тела
a
Fр
m
Fр a m
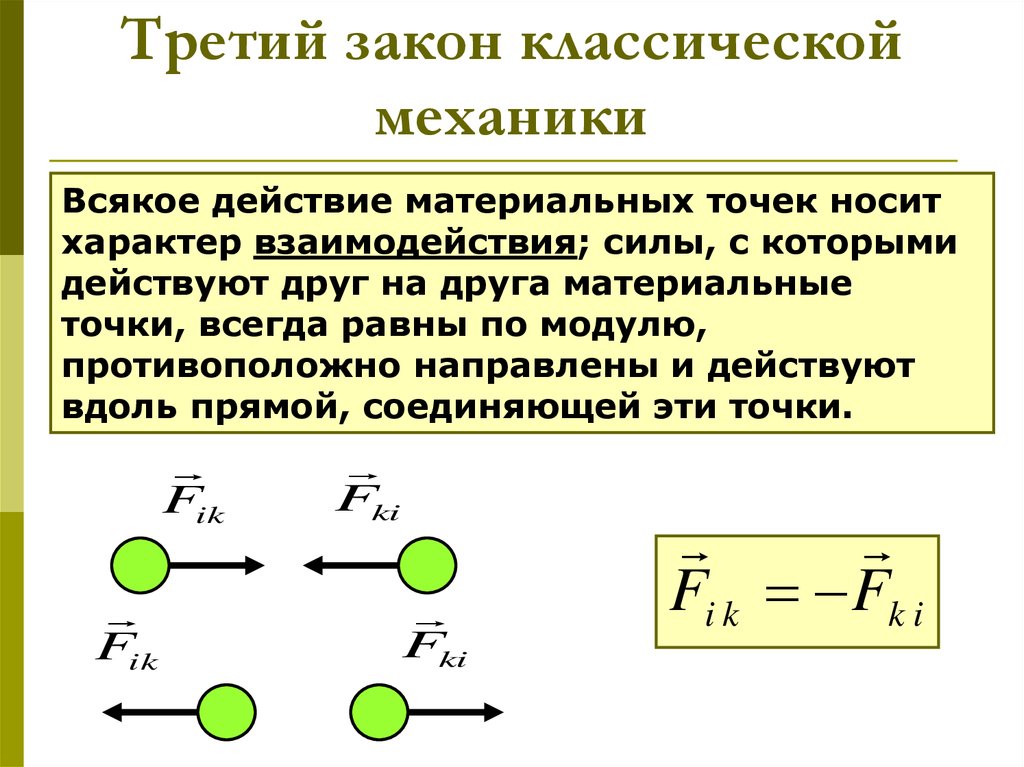
10. Третий закон классической механики
Всякое действие материальных точек носитхарактер взаимодействия; силы, с которыми
действуют друг на друга материальные
точки, всегда равны по модулю,
противоположно направлены и действуют
вдоль прямой, соединяющей эти точки.
Fik
Fik
Fki
Fki
Fi k Fk i
11. Замечания
III закон говорит о равенстве сил,приложенных к различным телам
III закон устанавливает связь между
силами одной природы
Сила, приложенная к одному из тел,
иногда называется действием, к другому –
противодействием или реакцией
12. Закон сохранения импульса
Механическая система – совокупностьматериальных точек, рассматриваемых как
единое целое.
Силы взаимодействия между материальными
точками системы называются внутренними.
Силы, с которыми на материальные точки
системы действуют внешние тела, называются
внешними.
Механическая система тел, на которую не
действуют внешние силы, называется
замкнутой (или изолированной).
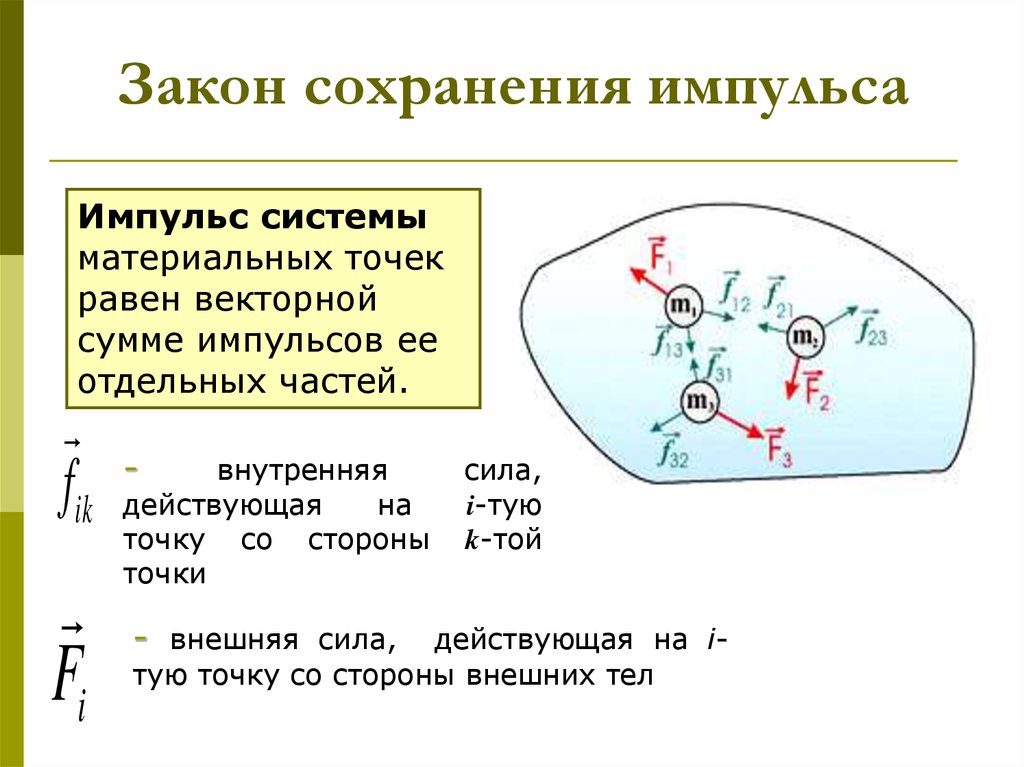
13. Закон сохранения импульса
Импульс системыматериальных точек
равен векторной
сумме импульсов ее
отдельных частей.
fik
Fi
-
внутренняя
действующая
на
точку со стороны
точки
- внешняя сила,
сила,
i-тую
k-той
действующая на iтую точку со стороны внешних тел
14. Закон сохранения импульса
dm1 1 f12 f13 ... f1N F1 ,
dt
d
m2 2 f 21 f 23 ... f 2 N F2 ,
dt
.......
d
mN N f N 1 f N 2 ... f NN 1 FN .
dt
d
mi i Fi
i 1 dt
i 1
N
N
Сумма
внутренних
сил, действующих на
точки системы, будет
равна нулю, так как
по
III
закону
классической
механики:
fik f ki
dp
dt
Fi
N
i 1
15. Закон сохранения импульса
Система называется замкнутой, если на неене действуют внешние тела, т.е.
Fi 0
Закон сохранения импульса системы точек:
импульс замкнутой системы остается величиной
постоянной при любых взаимодействиях между
точками системы
dp
dt
0
dp 0
p const
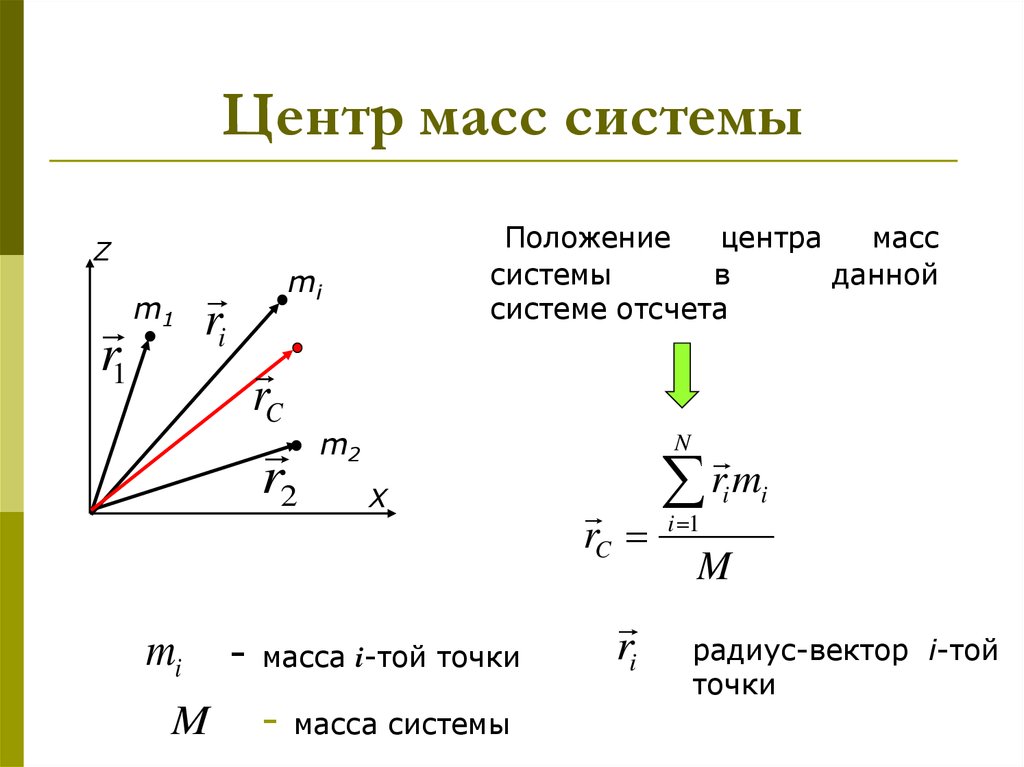
16. Центр масс системы
Zm
r1
1
mi
ri
rC
r2
mi
M
Положение
центра
масс
системы
в
данной
системе отсчета
-
m2
X
масса i-той точки
-
ri mi
N
масса системы
rC
ri
i 1
M
радиус-вектор i-той
точки
17. Определение центра масс С системы из двух точек
Векторнаяформа:
- координатная форма
18. Закон движения центра масс
Nri mi
d i 1
1
С
dt M M
pс
-
N
dri
mi
dt
i 1
N
импульс системы
m
i 1
i
M
i
pi
N
i 1
M
pс
M
pс M C
Скорость центра масс замкнутой системы остается
величиной
постоянной,
т.е.
центр
масс
замкнутой системы движется прямолинейно
равномерно. Центр масс иногда называют
центром инерции
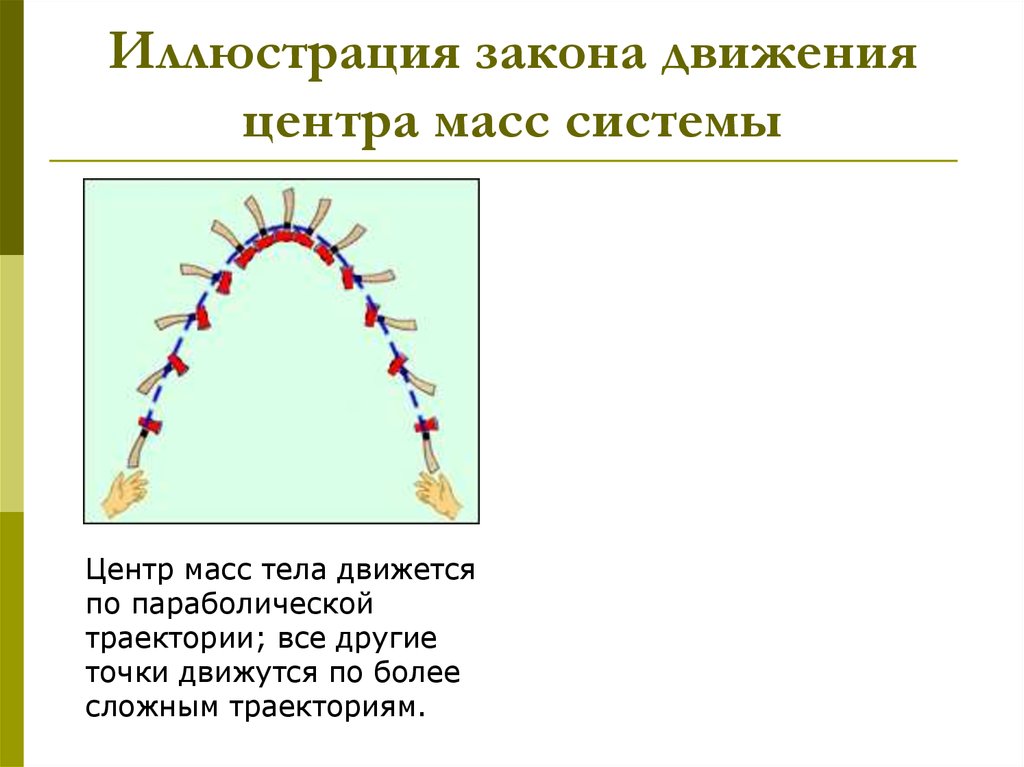
19. Иллюстрация закона движения центра масс системы
Центр масс тела движетсяпо параболической
траектории; все другие
точки движутся по более
сложным траекториям.
20. Иллюстрация закона движения центра масс системы
Стробоскопическая фотография движения гаечного ключа,скользящего по гладкой поверхности и вращающегося
вокруг своего центра масс.
Красной точкой обозначен центр масс тела.














 Физика
Физика








