Продольные и поперечные волны. Уравнение плоской гармонической волны. Стоячие волны

1. Волны

Продольные и поперечные волны
Уравнение плоской гармонической
волны
Стоячие волны

2. Волны в природе

Волной называется процесс распространения колебаний в
сплошной среде, периодический во времени и пространстве
Волны в открытом океане
Волны вблизи берега

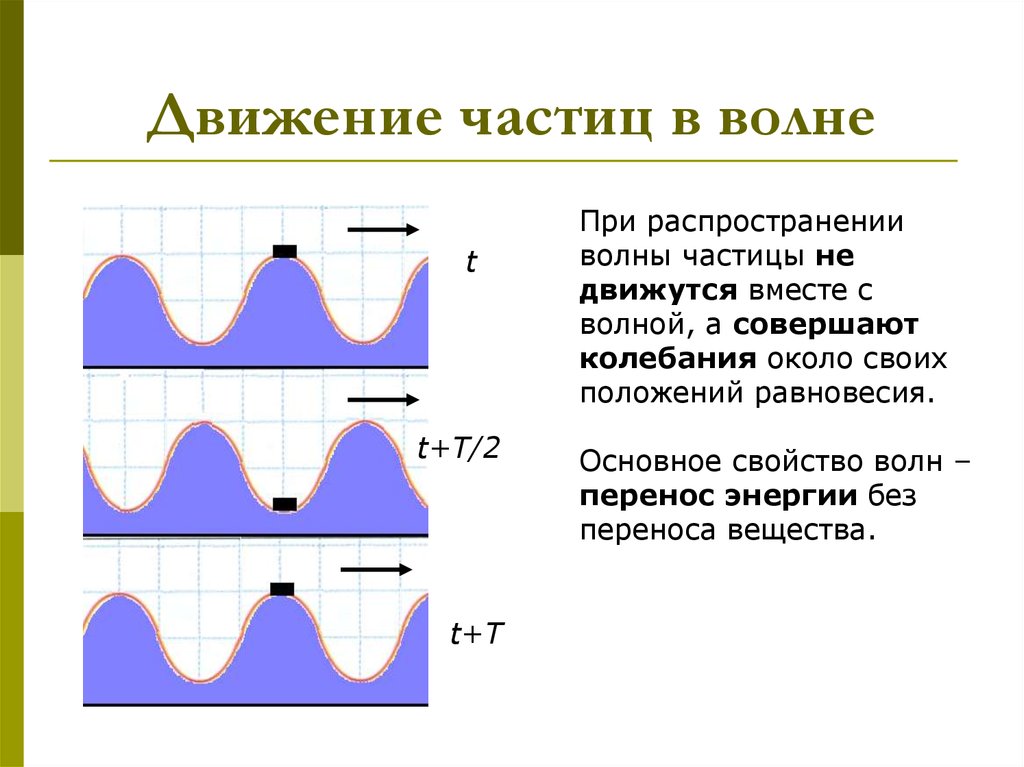
3. Движение частиц в волне

t
t+T/2
t+T
При распространении
волны частицы не
движутся вместе с
волной, а совершают
колебания около своих
положений равновесия.
Основное свойство волн –
перенос энергии без
переноса вещества.

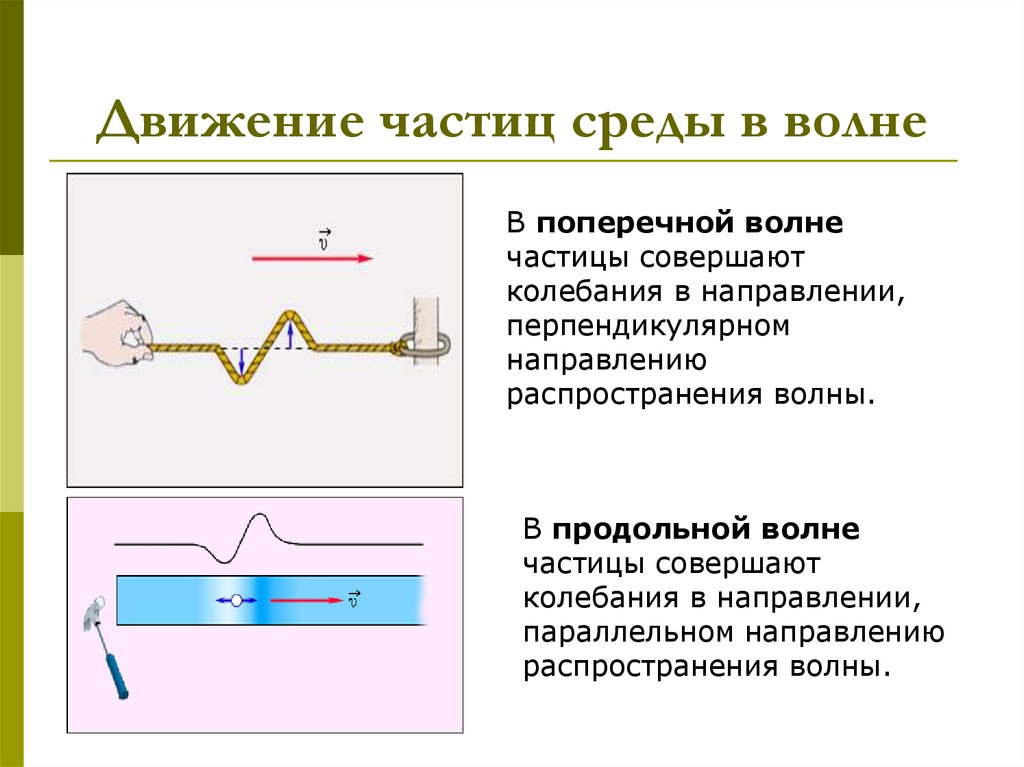
4. Движение частиц среды в волне

В поперечной волне
частицы совершают
колебания в направлении,
перпендикулярном
направлению
распространения волны.
В продольной волне
частицы совершают
колебания в направлении,
параллельном направлению
распространения волны.

5. Теоретическая модель поперечной волны

6. Теоретическая модель продольной волны

7. Уравнение бегущей волны

x, t A cos t kx 0
ξ – смещение частиц
фаза волны
λ – длина волны – расстояние
между ближайшими частицами,
колеблющимися в одинаковой фазе
t kx 0 const
dx
фазовая скорость волны
dt
k
от положения
равновесия
ω - частота
k – волновое число
- начальная фаза
0
T
2
k

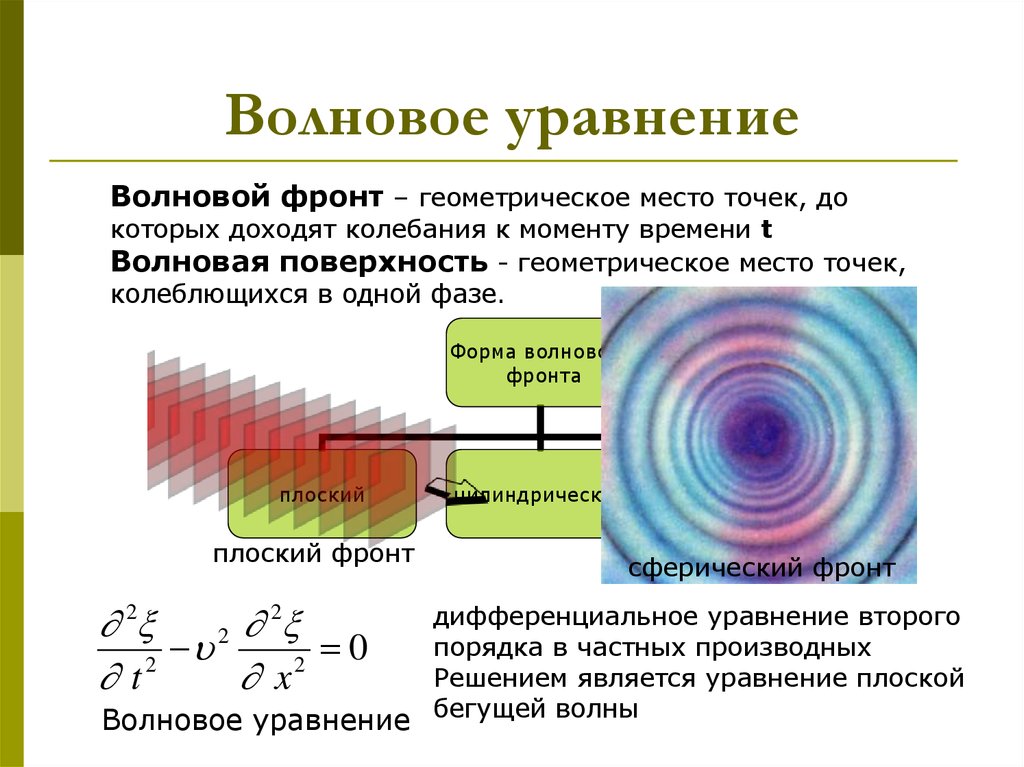
8. Волновое уравнение

Волновой фронт – геометрическое место точек, до
которых доходят колебания к моменту времени t
Волновая поверхность - геометрическое место точек,
колеблющихся в одной фазе.
Форма волнового
фронта
плоский
плоский фронт
2
2
2
0
2
2
t
x
цилиндрический
сферический
сферический фронт
дифференциальное уравнение второго
порядка в частных производных
Решением является уравнение плоской
Волновое уравнение бегущей волны

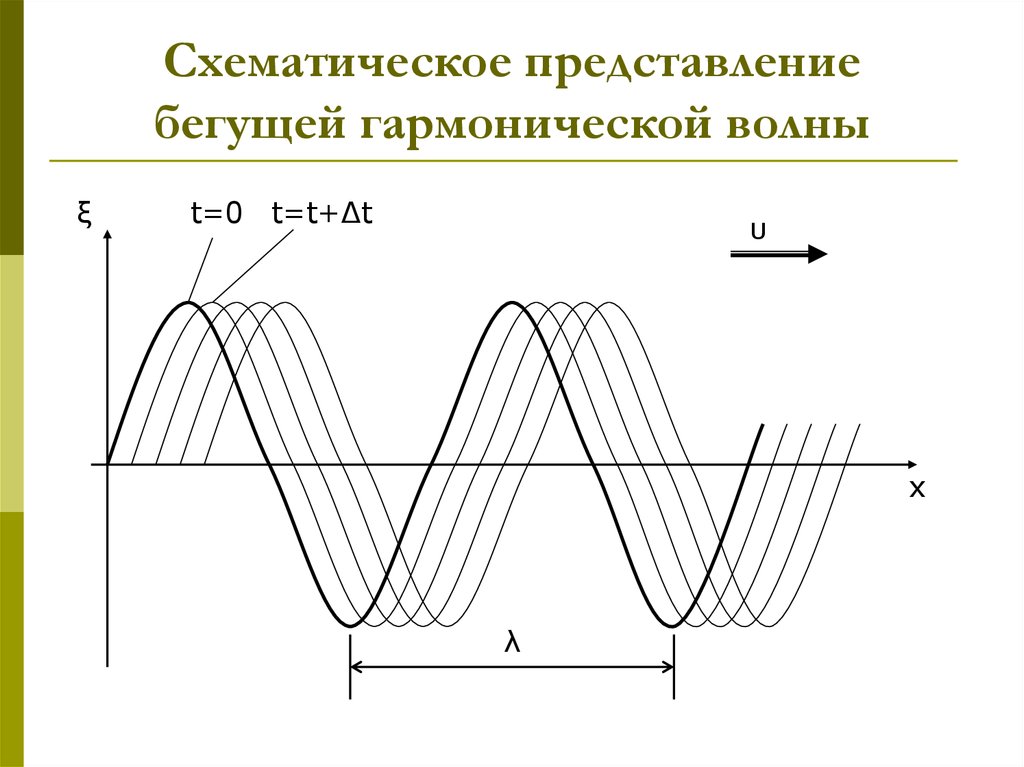
9. Схематическое представление бегущей гармонической волны

ξ
t=0 t=t+Δt
υ
x
λ

10. Стоячие волны

Стоячие волны образуются при наложении 2-х бегущих
гармонических волн, распространяющихся навстречу друг другу
с одинаковыми частотами и амплитудами
1 A cos t kx
2 A cos t kx
x
1 2 2 A cos 2 cos t
Отличия стоячей волны от бегущей:
•все точки между соседними узлами колеблются в одной фазе
•фаза колебаний изменяется на π при переходе через узел
•каждая точка среды имеет свою амплитуду
•в случае стоячей волны отсутствует перенос энергии (между
двумя узлами кинетическая энергия переходит в
потенциальную и обратно)

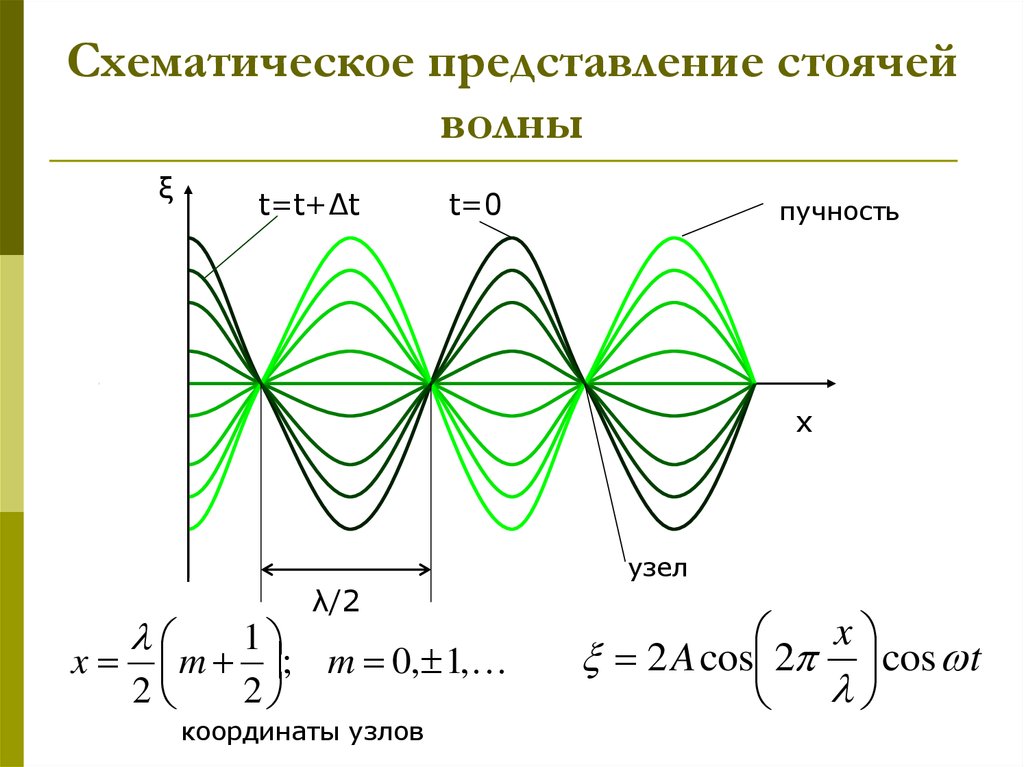
11. Схематическое представление стоячей волны

ξ
t=t+Δt
t=0
пучность
x
узел
λ/2
1
x m ; m 0, 1,
2
2
координаты узлов
x
2 A cos 2 cos t