Строительные конструкции. Изгибаемые элементы таврового профиля

1. Изгибаемые элементы таврового профиля

Строительные конструкции - 1
9 лекция
Изгибаемые элементы
таврового профиля
Области применения и размеры
Расчетные случаи
08.11.2018
1

2.

9 лекция
Строительные конструкции - 1
Области применения и размеры
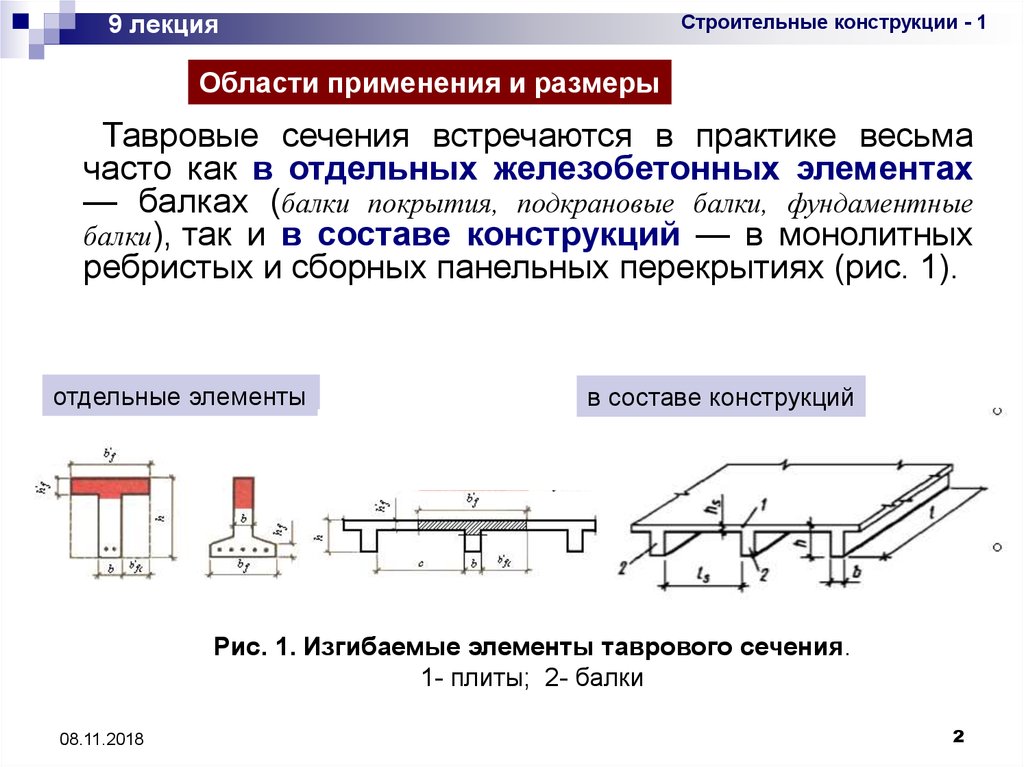
Тавровые сечения встречаются в практике весьма
часто как в отдельных железобетонных элементах
— балках (балки покрытия, подкрановые балки, фундаментные
балки), так и в составе конструкций — в монолитных
ребристых и сборных панельных перекрытиях (рис. 1).
отдельные элементы
в составе конструкций
Рис. 1. Изгибаемые элементы таврового сечения.
1- плиты; 2- балки
08.11.2018
2

3.

Строительные конструкции - 1
Тавровое сечение образуется из полки и ребра.
В сравнении с прямоугольным (см. рис. 2) тавровое
сечение значительно выгоднее, ибо при одной и той же
несущей
способности
(несущая
способность
железобетонного элемента не зависит от площади сечения
бетона растянутой зоны) расходуется бетона меньше
вследствие сокращения размеров растянутой зоны. По той
же причине более целесообразно тавровое сечение с
полкой в сжатой зоне, так как полка в растянутой зоне не
повышает несущей способности элемента.
bf
x
hf
bf l
h
bf
bf
x
hf
x
h
hf
b
Рис. 2. Несущая способность приведенных сечений одинакова
Тавровое сечение, как правило, имеет одиночное
армирование.
08.11.2018
3

4.

Строительные конструкции - 1
При большой ширине полок участки свесов, более
удаленные от ребра, напряжены меньше. Поэтому в
расчет вводят эквивалентную ширину свесов полки
bf1 (рис. 1). Она принимается равной:
bf1 — не более половины
расстояния в свету между ребрами с и не более 1/6
1) в каждую сторону от ребра
пролета рассчитываемого элемента
hf ≥ 0,1h
bf ≤ b+12·hf
если
0,05h ≤ hf < 0,1h
bf ≤ b+6·hf
если
hf < 0,05h
bf = b
2) если
08.11.2018
4

5.

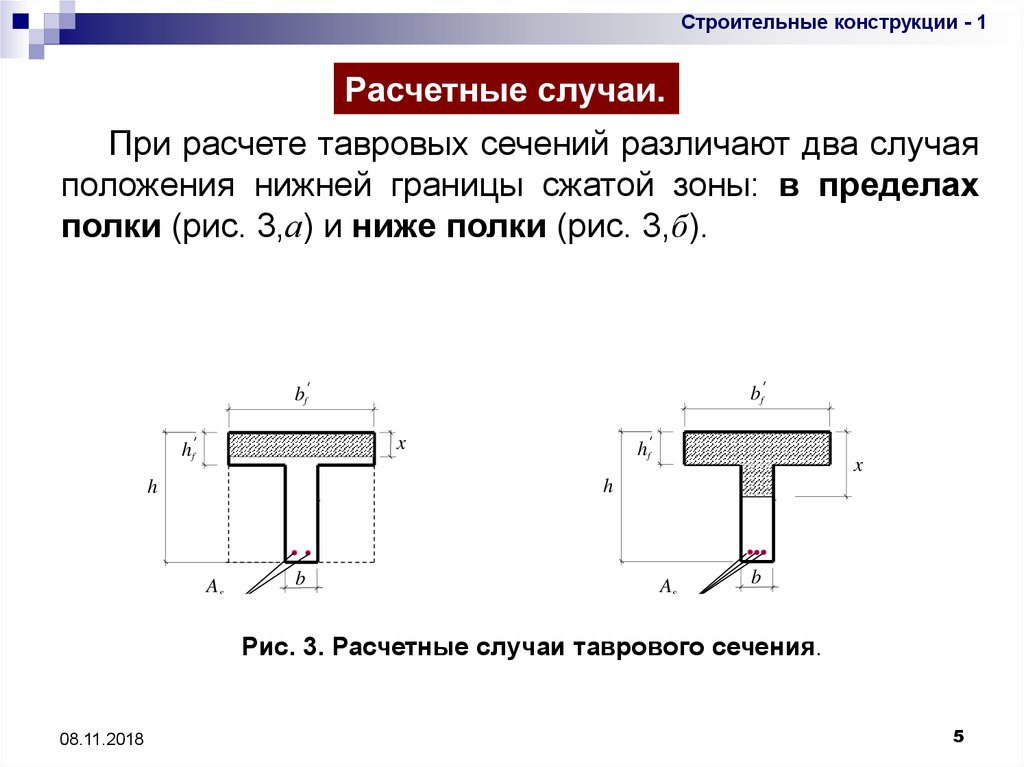
Строительные конструкции - 1
Расчетные случаи.
При расчете тавровых сечений различают два случая
положения нижней границы сжатой зоны: в пределах
полки (рис. 3,а) и ниже полки (рис. 3,б).
bf
bf
x
hf
hf
x
h
h
As
b
As
b
Рис. 3. Расчетные случаи таврового сечения.
08.11.2018
5

6.

Строительные конструкции - 1
Как определяется расчетный случай?
Сначала определяется ширина полки bf=b+2 bfl затем,
а) если известны все характеристики поперечного
сечения:
∑x=0;
Ns=Nb
Rs·As ≤ Nper= Rb·bf ·hf
(1)
Если условие выполняется, то тавровое сечение
рассчитывается по 1-му расчетному случаю, т.е. x ≤ hf
Если условие не выполняется, то тавровое сечение
рассчитывается по 2-му расчетному случаю, т.е. x > hf
08.11.2018
6

7.

Строительные конструкции - 1
б) если известны все характеристики поперечного
сечения кроме, Аs:
∑x=0;
Ns=Nb
M ≤ Mper= Rb·bf ·hf (ho-0,5hf )
(2)
Если условие выполняется, то тавровое сечение
рассчитывается по 1-му расчетному случаю, т.е. x ≤ hf
Если условие не выполняется, то тавровое сечение
рассчитывается по 2-му расчетному случаю, т.е. x > hf
08.11.2018
7

8.

Строительные конструкции - 1
1-й расчетный случай.
bf
Нейтраль. ось
Rb
h
M
b
z=(ho-0,5x )
x
hf
Nb=Rb·bf·x
Ns=Rs·As
Рис. 4. Тавровое сечение, как прямоугольное .
Нижняя граница сжатой зоны располагается в пределах полки, т. е.
x ≤ hf в сечениях с развитыми свесами.
В этом случае тавровое сечение рассчитывают как
прямоугольное с размерами bf и hо (пунктир на рис.4,а), поскольку
площадь бетона в растянутой зоне на несущую способность не
влияет.
При этом схема усилий и эпюра напряжений в сжатом бетоне
остаются такими же, как и при расчёте прямоугольных сечений.
Расчётными формулами являются:
08.11.2018
8

9.

Строительные конструкции - 1
1-й расчетный случай.
M R b bf x h 0 0,5x
R s As R b b f x
(3)
(4)
Преобразуя (3), получим
2
M m R b bf h 0 ,
где αm-коэффициент, определяемый по табличным
данным или по формуле
m 1 ;
2
08.11.2018
9

10.

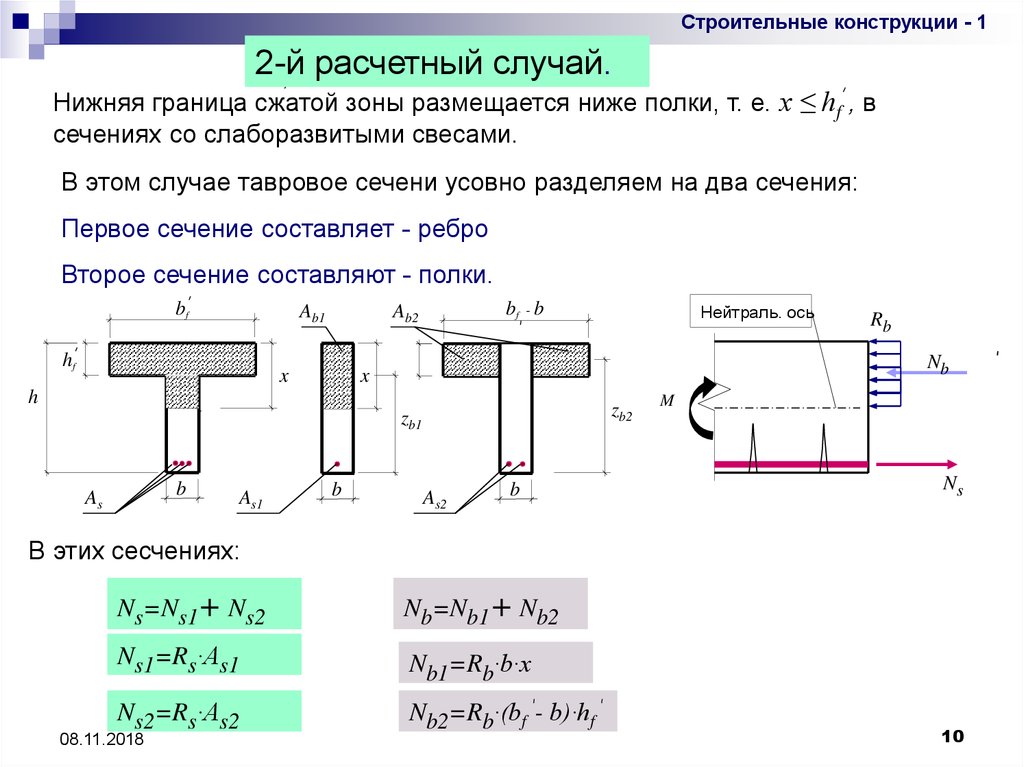
Строительные конструкции - 1
2-й расчетный случай.
Нижняя граница сжатой зоны размещается ниже полки, т. е. x ≤ hf , в
сечениях со слаборазвитыми свесами.
В этом случае тавровое сечени усовно разделяем на два сечения:
Первое сечение составляет - ребро
Второе сечение составляют - полки.
bf
hf
bf - b
Ab2
Ab1
x
zb2
zb1
b
As1
b
Rb
Nb
x
h
As
Нейтраль. ось
As2
b
M
Ns
В этих сесчениях:
Ns=Ns1+ Ns2
Nb=Nb1+ Nb2
Ns1=Rs·As1
Nb1=Rb·b·x
Ns2=Rs·As2
Nb2=Rb·(bf - b)·hf
08.11.2018
10

11.

Строительные конструкции - 1
bf
hf
bf - b
Ab2
Ab1
x
zb2
zb1
b
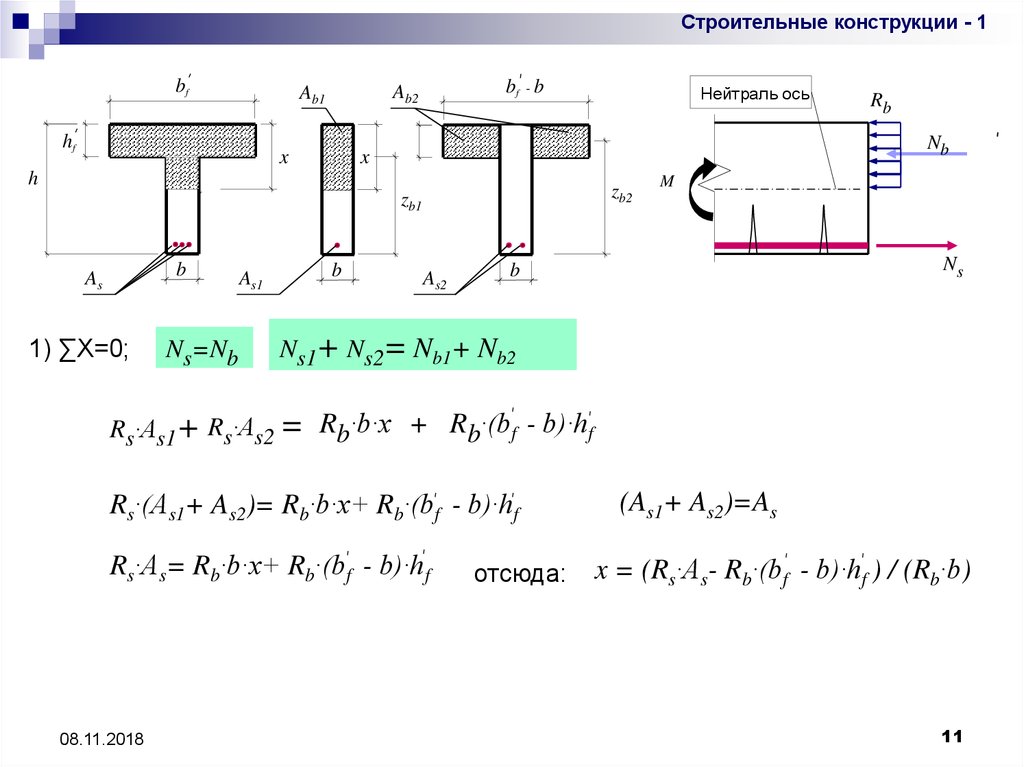
1) ∑X=0;
Ns=Nb
As1
b
Rb
Nb
x
h
As
Нейтраль ось
As2
M
Ns
b
Ns1+ Ns2= Nb1+ Nb2
Rs·As1+ Rs·As2 = Rb·b·x + Rb·(bf - b)·hf
Rs·(As1+ As2)= Rb·b·x+ Rb·(bf - b)·hf
Rs·As= Rb·b·x+ Rb·(bf - b)·hf
08.11.2018
отсюда:
(As1+ As2)=As
x = (Rs·As- Rb·(bf - b)·hf ) / (Rb·b)
11

12.

Строительные конструкции - 1
bf
hf
bf - b
Ab2
Ab1
x
Nb
zb2
zb1
b
As1
Rb
x
h
As
Нейтраль ось
b
M
Ns
b
As2
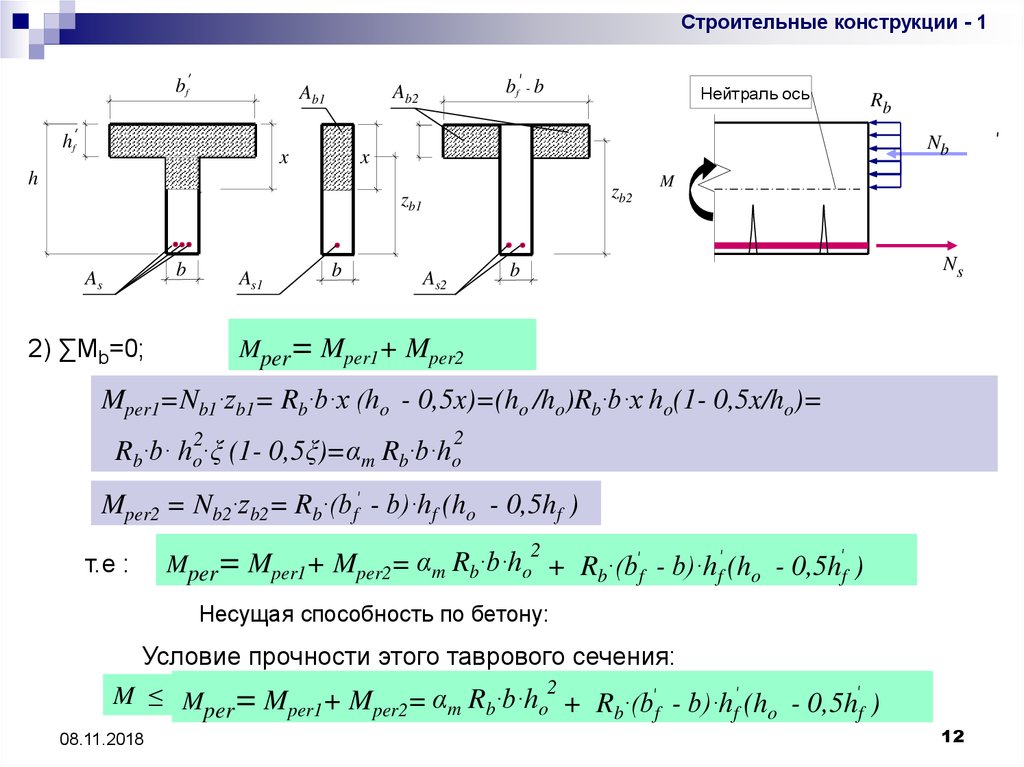
Mper= Mper1+ Mper2
2) ∑Mb=0;
Mper1=Nb1·zb1= Rb·b·x (ho - 0,5x)=(ho /ho)Rb·b·x ho(1- 0,5x/ho)=
2
2
Rb·b· ho·ξ (1- 0,5ξ)=αm Rb·b·ho
Mper2 = Nb2·zb2= Rb·(bf - b)·hf (ho - 0,5hf )
2
Mper= Mper1+ Mper2= αm Rb·b·ho + Rb·(bf - b)·hf (ho - 0,5hf )
т.е :
Несущая способность по бетону:
Условие прочности этого таврового сечения:
M ≤ M = Mper1+ Mper2= αm Rb·b·ho2 + R ·(b - b)·h (h - 0,5h )
per
b
f
f
o
f
08.11.2018
12

13.

Строительные конструкции - 1
bf
hf
bf - b
Ab2
Ab1
x
zb2
zb1
b
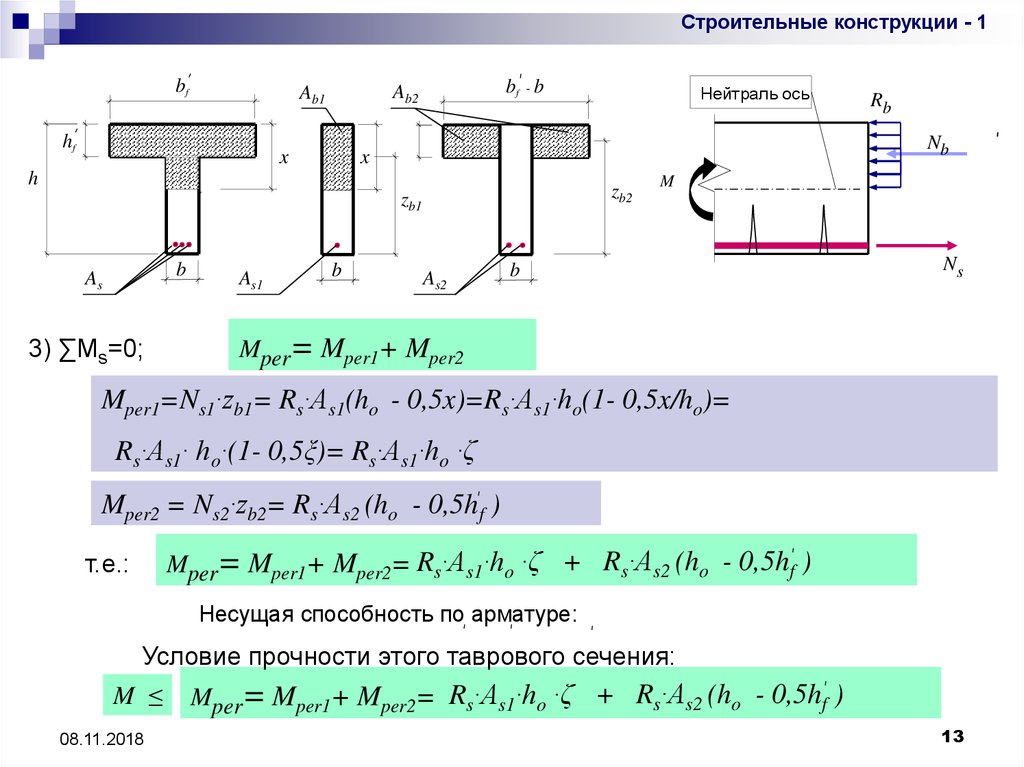
3) ∑Ms=0;
As1
b
Rb
Nb
x
h
As
Нейтраль ось
As2
M
b
Ns
Mper= Mper1+ Mper2
Mper1=Ns1·zb1= Rs·As1(ho - 0,5x)=Rs·As1·ho(1- 0,5x/ho)=
Rs·As1· ho·(1- 0,5ξ)= Rs·As1·ho ·ζ
Mper2 = Ns2·zb2= Rs·As2 (ho - 0,5hf )
Mper= Mper1+ Mper2= Rs·As1·ho ·ζ + Rs·As2 (ho - 0,5hf )
т.е.:
Несущая способность по арматуре:
Условие прочности этого таврового сечения:
M ≤
08.11.2018
Mper= Mper1+ Mper2= Rs·As1·ho ·ζ + Rs·As2 (ho - 0,5hf )
13