Гидростатика

1. ГИДРОСТАТИКА

*
Гидростатика
это
раздел
гидромеханики, в котором изучаются
условия и закономерности равновесия
жидкостей под действием приложенных к
ним сил, а также воздействия покоящихся
жидкостей на погруженные в них тела и на
стенки сосудов.

2.

Общие представления о жидкостях и их свойствах
Капельные и упругие жидкости В теории гидромеханики под
термином «жидкость» подразумеваются капельные и упругие
жидкости (газы и пары) благодаря их общему физическому
свойству – текучести. Поэтому, прежде всего, в гидравлике и
гидромеханических процессах жидкости рассматриваются как
текучие среды (вещества), способные самопроизвольно занимать и
принимать форму всего объѐма сосуда, в котором они заключены.
Кроме того, жидкости представляются как сплошные среды с
непрерывно распределенной плотностью. Под этим понятием
имеется в виду среда, частицы которой равномерно распределены
по всему еѐ объѐму без « разрывов», т.е. в любой точке объѐма
существуют частицы среды и обладают определѐнной плотностью.

3.

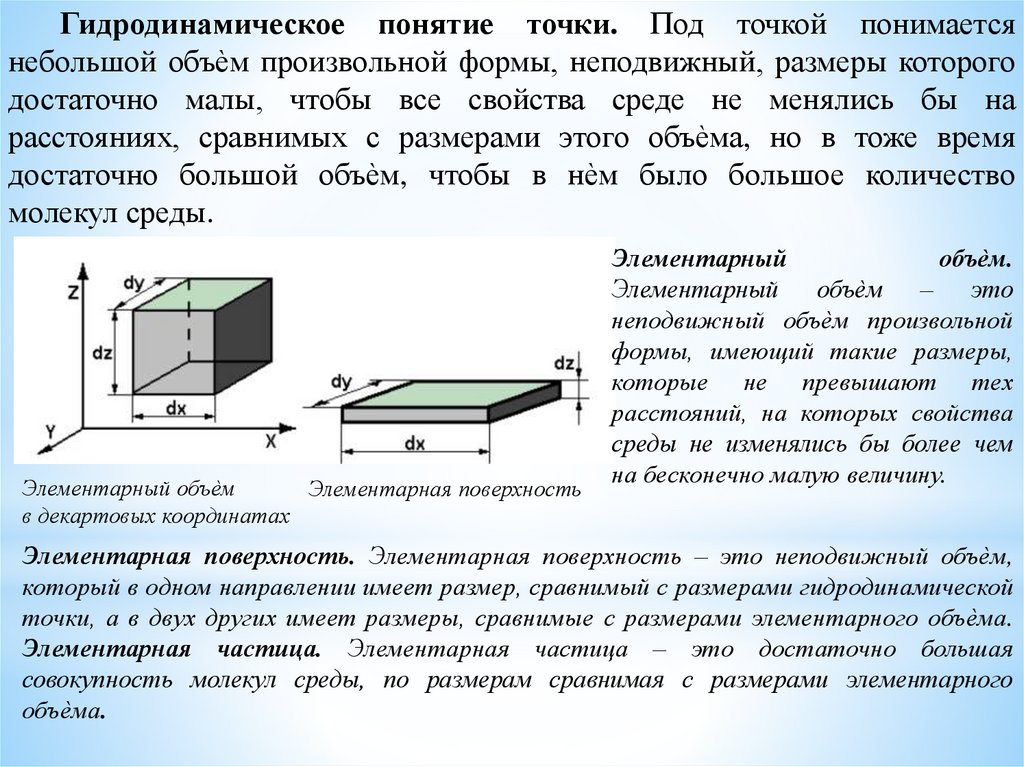
Гидродинамическое понятие точки. Под точкой понимается
небольшой объѐм произвольной формы, неподвижный, размеры которого
достаточно малы, чтобы все свойства среде не менялись бы на
расстояниях, сравнимых с размерами этого объѐма, но в тоже время
достаточно большой объѐм, чтобы в нѐм было большое количество
молекул среды.
Элементарный объѐм
Элементарная поверхность
в декартовых координатах
Элементарный
объѐм.
Элементарный объѐм – это
неподвижный объѐм произвольной
формы, имеющий такие размеры,
которые не превышают тех
расстояний, на которых свойства
среды не изменялись бы более чем
на бесконечно малую величину.
Элементарная поверхность. Элементарная поверхность – это неподвижный объѐм,
который в одном направлении имеет размер, сравнимый с размерами гидродинамической
точки, а в двух других имеет размеры, сравнимые с размерами элементарного объѐма.
Элементарная частица. Элементарная частица – это достаточно большая
совокупность молекул среды, по размерам сравнимая с размерами элементарного
объѐма.

4.

Сведения из теории
На жидкость, находящуюся в состоянии покоя, действуют силы, которые
можно разделить на поверхностные и массовые.
Поверхностные силы приложены к частицам жидкости, находящимся на
поверхности раздела данной жидкости и другой среды (реакция стенки сосуда,
сила давления поршня, сила давления газа на свободную поверхность).
Массовые силы воздействуют на все частицы данного объема жидкости и
пропорциональны массе каждой частицы (силы тяжести, силы инерции,
центробежные силы).
Основным понятием гидростатики является понятие гидростатического
давления.
Выделим, в находящейся в равновесии жидкости, некоторый объем
произвольной формы. Рассечем его на две части I и II плоскостью AB
Воздействие части I жидкости на часть II будет
передаваться по плоскости раздела AB. Выделим на
плоскости раздела площадку площадью ∆s. Заменим
воздействие части I на эту площадку силой ∆Р. Сила
воздействия ∆Р приходящаяся на эту площадку,
называется силой гидростатического давления.

5.

Отношение силы к площади:
∆Р
рср = ∆s
представляет среднее гидростатическое давление.
Если площадь ∆s стремится к 0, то отношение ∆Р/∆s будет стремиться к пределу,
который называется гидростатическим давлением в точке:
∆Р
p= lim ∆s
∆s→0
Гидростатическое давление направлено всегда по внутренней нормали к
площадке, на которой это давление действует и является сжимающим
напряжением, потому что в покоящейся жидкости не могут существовать
касательные и растягивающие усилия. Величина гидростатического давления в
любой точке жидкости по всем направлениям одинакова.
Гидростатическое давление зависит от положения рассматриваемой точки
внутри жидкости и от внешнего давления, действующего на свободной
поверхности жидкости. Гидростатическое давление имеет размерность
напряжения, т.е. сила/площадь. Измеряют давление в Н/м2 (Паскаль).

6.

В гидравлике, как правило, наиболее употребительны две из
них: техническая МКГСС (метр-килограмм-сила- секунда) и
международная система СИ.
В системе МКГСС за основные приняты единицы: длины - метр
(м), силы - килограмм-сила (кгс), времени - секунда (сек). 1 кгс
представляет собой силу, сообщающую 1 килограмму массы (кг)
ускорение, равное ускорению свободного падения g = 9,81 м/сек2.
Иногда в задачах вы можете встретить кГ, что означает тоже
килограмм-сила, т.е., например, давление 1 кгс/м2 то же самое, что и
1 кГ / м2
Ньютон (Н) - сила, сообщающая телу массой 1 кг ускорение 1м/с
в направлении действия силы.
Паскаль (Па) - давление, вызываемое силой 1 Н, равномерно
распределенной по поверхности площадью 1 м2.
Атмосферное давление измеряют технической атмосферой
равной 98100 Па или физической равной 101325 Па, иногда
используется единица бар (1бар=105Па).

7.

Единица Па (Н/м2)
кгс/см2
(ат)
кгс/м2
мм вод.
ст.
м
вод. ст.
мм рт. ст.
бар
1 Па (Н/м2)
1
10,2∙10-6
0,102
0,102
102∙10 -6
750∙10-5
10-5
1 кгс/см2
(ат)
9,81∙104
1
104
104
10
735,6
0,981
1 кгс/м2
9,81
104
1
1
10-3
73,56∙10 -3
98,1∙10-6
1 мм вод. ст.
9,81
10-4
1
1
10-3
73,56∙10-3
98,1∙10 -6
1м
вод. ст.
9,8∙103
0,1
103
103
1
73,56
98,1∙10-3
1 мм рт. ст.
133,3
1,36∙10 -3
13,6
13,6
13,6∙10-3
1
1,33∙10-3
1 бар
105
1,02
10,2
750
1
10,2∙103 10,2-103

8.

Различают давление абсолютное (иногда употребляют термин
‘’полное‘’) и избыточное. Абсолютным называется давление,
определённое с учетом атмосферного давления. Избыточное давление
это давление сверх атмосферного, определенное без учета
атмосферного.
Рабс=Ратм+Ризб ;
Ризб=Рабс - Ратм.
Абсолютное давление не может быть отрицательным, так как
жидкость не воспринимает растягивающих напряжений Рабс ≥ 0.
Избыточное давление может быть и больше и меньше нуля 0 ≤ Ризб ≥ 0.
Для удобства, отрицательное избыточное давление, взятое со знаком
плюс, называют вакуумметрическим давлением:
-Ризб = Рвак
Очень часто избыточное давление называют манометрическим, так
как оно измеряется с помощью манометров, или пьезометрическим, так
как оно измеряется с помощью пьезометров.

9.

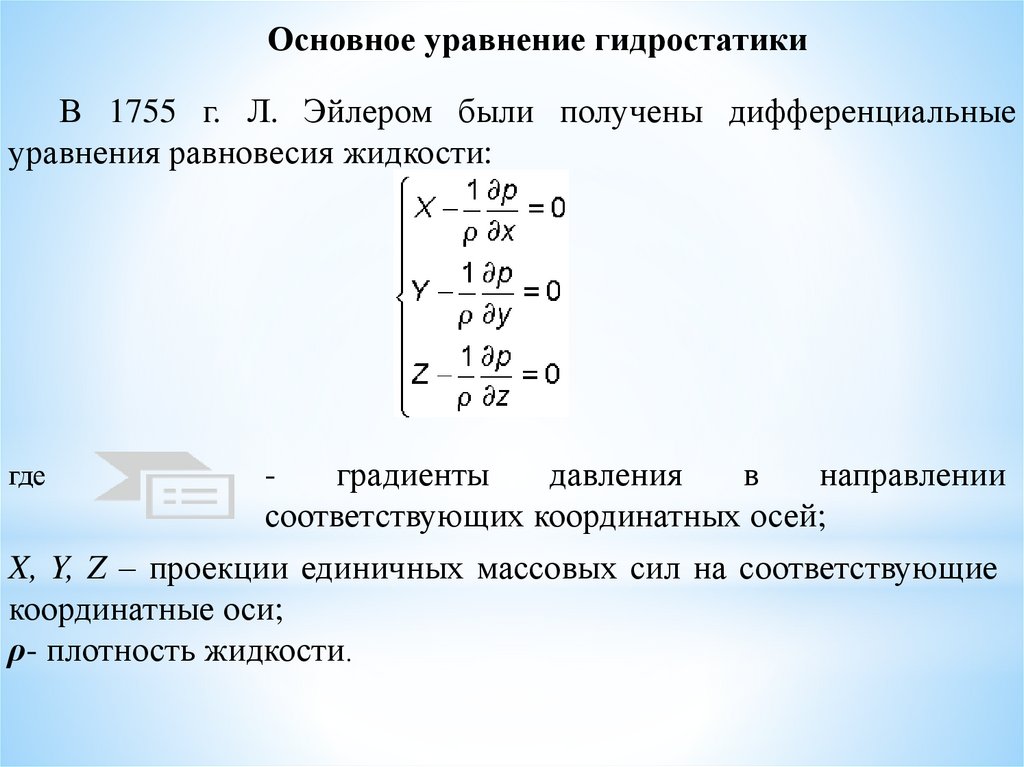
Основное уравнение гидростатики
В 1755 г. Л. Эйлером были получены дифференциальные
уравнения равновесия жидкости:
где
градиенты
давления
в
направлении
соответствующих координатных осей;
X, Y, Z – проекции единичных массовых сил на соответствующие
координатные оси;
ρ- плотность жидкости.

10.

После незначительных преобразований данную
уравнений можно представить в виде уравнения
систему
Полученное уравнение выражает изменение давления вдоль
координатных осей в общем случае равновесия, и называется
основным дифференциальным уравнением гидростатики.
Поверхностью уровня называется такая поверхность, во всех
точках которой рассматриваемая функция имеет одно и то же
значение. Для задач гидравлики особое значение имеет
поверхность равного давления. Эту поверхность будем называть
поверхностью уровня.

11.

Так как во всех точках поверхности уровня гидростатическое
давление одинаково, то есть р=const, то dp=0. Из основного
дифференциального уравнения гидростатики имеем:
поскольку плотность не равна нулю ρ≠0, запишем
поверхность уровня имеет следующие свойства:
1) две поверхности уровня не пересекаются между собой;
2) массовые силы направлены нормально к поверхности уровня.
Поверхность уровня на границе жидкой и газообразной среды
называется свободной поверхностью.

12.

Давление при абсолютном покое
Рассмотрим случаи равновесия жидкости, находящейся в сосуде,
в состоянии абсолютного покоя под действием сил тяжести и
внешнего давления на свободной поверхности. В этом случае
проекции единичной силы тяжести на координатные оси равны:
Х = 0; Y = 0; z = - g.
После подстановки в уравнение
получаем
После интегрирования имеем

13.

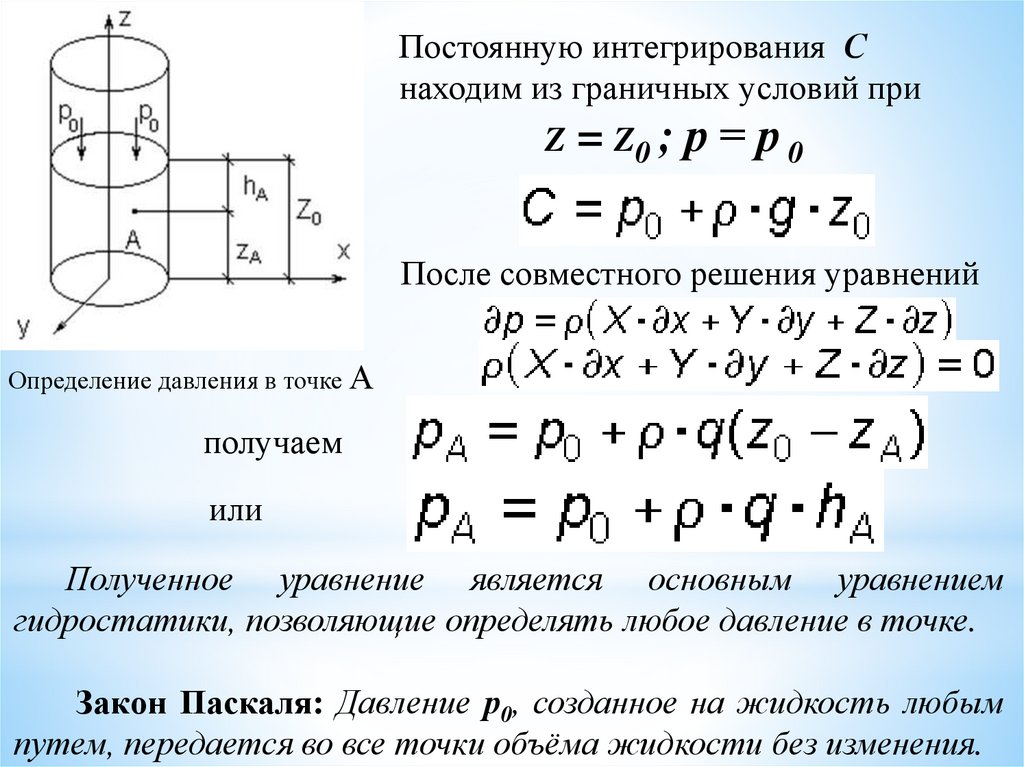
Постоянную интегрирования С
находим из граничных условий при
Z
= Z0 ; р = р 0
После совместного решения уравнений
Определение давления в точке А
получаем
или
Полученное уравнение является основным уравнением
гидростатики, позволяющие определять любое давление в точке.
Закон Паскаля: Давление р0, созданное на жидкость любым
путем, передается во все точки объёма жидкости без изменения.

14.

Поверхность уровня при абсолютном покое
Дифференциальное уравнение поверхности уровня в этом случае
имеет вид:
- g ∙ dZ = 0 или dZ =0
интегрируя, находим Z = const = C.
Так как C = const - произвольная постоянная, то это уравнение
будет уравнением семейства горизонтальных плоскостей. Таким
образом, поверхность уровня есть горизонтальная плоскость,
следовательно, и свободная поверхность будет горизонтальной
плоскостью.

15.

Анализ основного уравнения гидростатики
Как уже отмечалось, основное уравнение гидростатики служит
для определения величины гидростатического давления в любой
точке покоящейся жидкости
Анализируя основное уравнение гидростатики можно сделать
следующие выводы:
1. Гидростатическое давление есть сумма внешнего p0 давления,
действующего на свободной поверхности и весового ρ ∙ g ∙ h
давления, создаваемого весом столба жидкости высотой h;
2. Внешнее давление p0 не зависит от координат рассматриваемых
точек, то есть оно передается во все точки покоящейся жидкости
без изменения, поэтому жидкость используется как среда для
передачи давления. На этом свойстве жидкости основано действие
гидравлических машин (гидропрессы, силовые цилиндры,
гидродомкраты);

16.

3. Весовое давление ρ ∙ g ∙ h является функцией координат точки. С
увеличением заглубления точки под свободную поверхность,
давление возрастает;
4. Внешнее давление p0 может быть больше атмосферного, меньше
атмосферного и равно атмосферному. Если численное значение p0
определено с учетом атмосферного, то давление p по формуле
будет абсолютным; если p0 определено без учета атмосферного,
то p будет избыточным.

17.

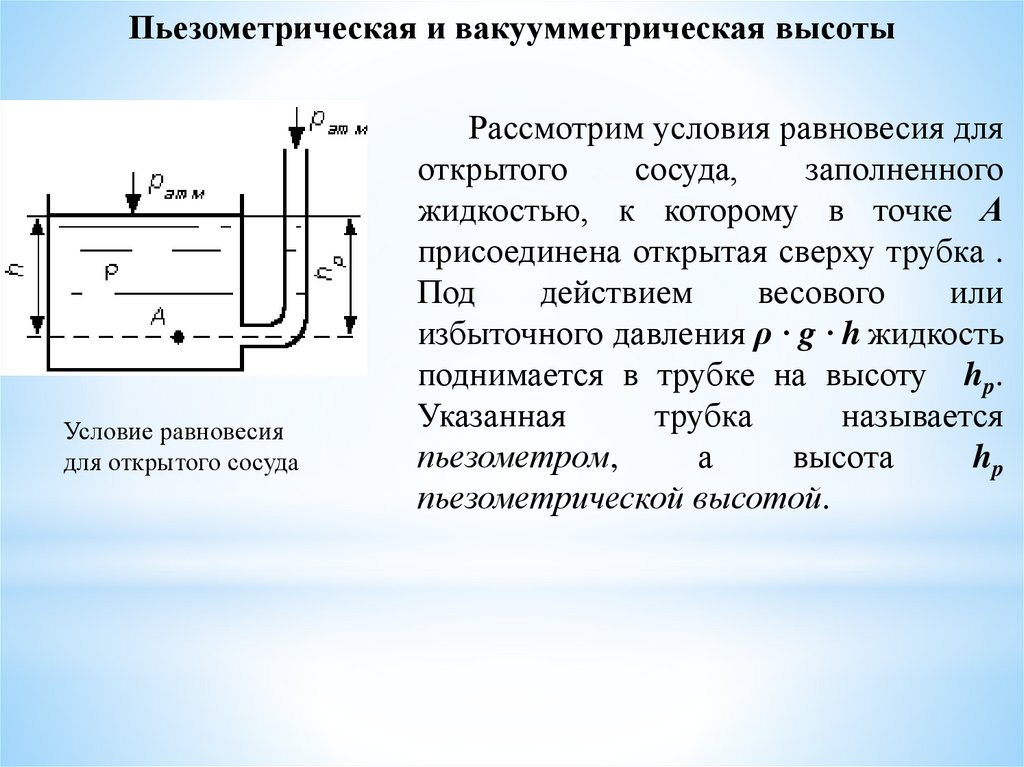
Пьезометрическая и вакуумметрическая высоты
Условие равновесия
для открытого сосуда
Рассмотрим условия равновесия для
открытого
сосуда,
заполненного
жидкостью, к которому в точке А
присоединена открытая сверху трубка .
Под
действием
весового
или
избыточного давления ρ ∙ g ∙ h жидкость
поднимается в трубке на высоту hp.
Указанная
трубка
называется
пьезометром,
а
высота
hp
пьезометрической высотой.

18.

Представим основное уравнение
гидростатики относительно плоскости,
проходящей через точку А. Давление в
точке
А
со
стороны
сосуда
определяется как:
со стороны пьезометра:
тогда:
или
то есть пьезометрическая высота показывает величину
избыточного давления в точке, где присоединен пьезометр в
линейных единицах размерности.

19.

Рассмотрим условия равновесия
теперь для закрытого сосуда, где
давление на свободной поверхности p0
больше атмосферного давления pатм.
Условие равновесия
для закрытого сосуда
Под действием давления p0 большего pатм и
весового давления ρ ∙ g ∙ h жидкость
поднимается в пьезометре на высоту hp
большую, чем в случае открытого сосуда.
Давление в точке А со стороны сосуда:
со стороны открытого пьезометра:
тогда:
из этого равенства получаем выражение для hp

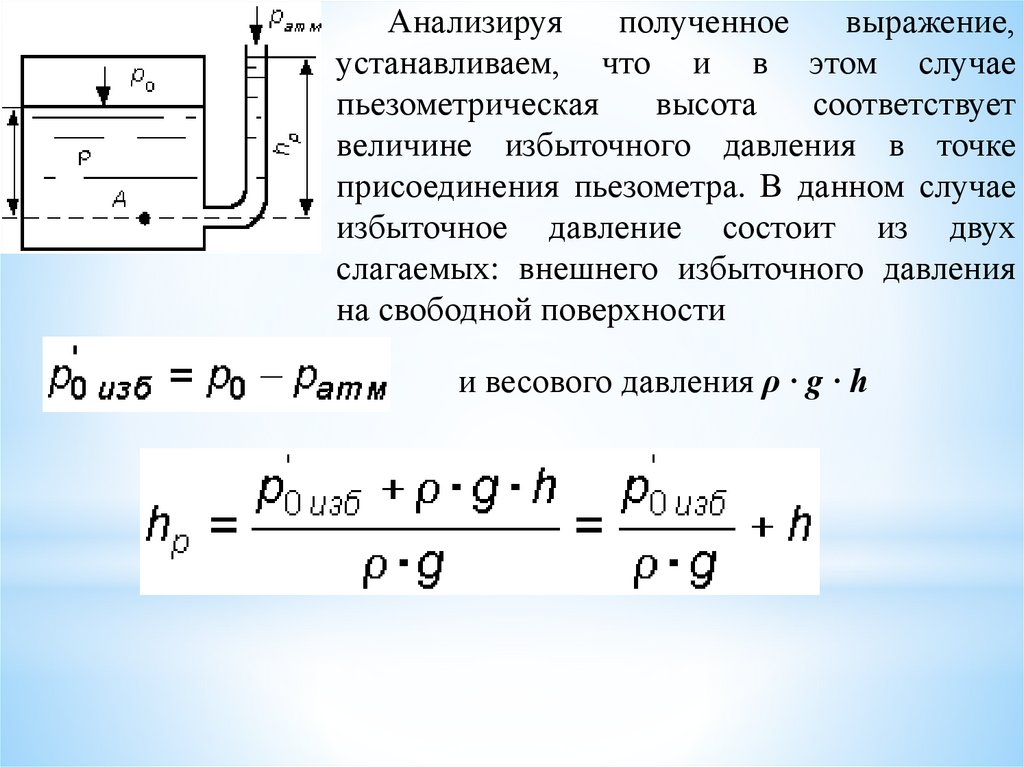
20.

Анализируя
полученное
выражение,
устанавливаем, что и в этом случае
пьезометрическая
высота
соответствует
величине избыточного давления в точке
присоединения пьезометра. В данном случае
избыточное давление состоит из двух
слагаемых: внешнего избыточного давления
на свободной поверхности
и весового давления ρ ∙ g ∙ h

21.

Избыточное давление может быть и отрицательной величиной,
называемой вакуумом. Так, во всасывающих патрубках
центробежных насосов, в потоке жидкости при истечении из
цилиндрических насадок, в вакуум – котлах в жидкости образуются
области с давлением ниже атмосферного, т.е. области вакуума.
В этом случае:

22.

Вакууметрическая высота
Вакуум – это недостаток давления до
атмосферного.
Пусть в резервуаре 1 абсолютное
давление
меньше
атмосферного
(например, откачана часть воздуха при
помощи вакуум-насоса). В резервуаре 2
находится жидкость, и резервуары
соединены изогнутой трубкой 3. На
поверхности жидкости в резервуаре 2
действует атмосферное давление.
Так как в резервуаре 1 давление меньше атмосферного, то жидкость
поднимается в трубке 3 на какую-то высоту, которая называется
вакуумметрической высотой и обозначается hВ. Эта величина может быть
определена из условия равновесия:
Максимальное значение вакуумметрического давления составляет
98,1кПа или 10 м.в.ст., но практически давление в жидкости не может
быть меньше давления паров насыщения и равно 7–8 м.в.ст.

23.

Условия равновесия жидкости в сообщающихся сосудах
Рассмотрим два сообщающихся сосуда, наполненных различными, не
смачивающимися между собой жидкостями.
Сообщающиеся сосуды
Сосуды закрыты, давления pO1 и pO2 - на
поверхности жидкостей в сосудах I и II
различны. Линия О-О – линия раздела
разнородных жидкостей. Горизонтальная
плоскость, проходящая через линию О-О,
является плоскостью равного давления.
Определим величину гидростатического
давления в точках С1 и С2 лежащих на
плоскости равного давления. Согласно
основному уравнению гидростатики:
Где h1 и h2 – возвышение поверхности жидкостей в сосудах I и II над
плоскостью О-О; ρ1 и ρ2 - плотности жидкостей.

24.

Очевидно, что:
Эта зависимость характеризует условия равновесия жидкостей в
сообщающихся сосудах. Она позволяет решать частные задачи.
Случай I. В сосудах налита одинаковая жидкость, но давления pO1 и pO2
различны, тогда при условии, что ρ1 = ρ2 = ρ. получим:
Случай II. Жидкость одинакова, т.е. ρ1 = ρ2 = ρ и pO1 = pO2
Тогда:
h 1 = h2
жидкость в сосудах будет на одном уровне.

25.

Случай III. Жидкость одинакова ρ1 = ρ2 =
ρ, но один сосуд открыт pO1 = pатм , а другой
закрыт pO1 > pатм . Тогда:
так как pС1 и pС2, значит
Выражение
есть пьезометрическая высота для точек,
лежащих на поверхности жидкости в
закрытом сосуде.

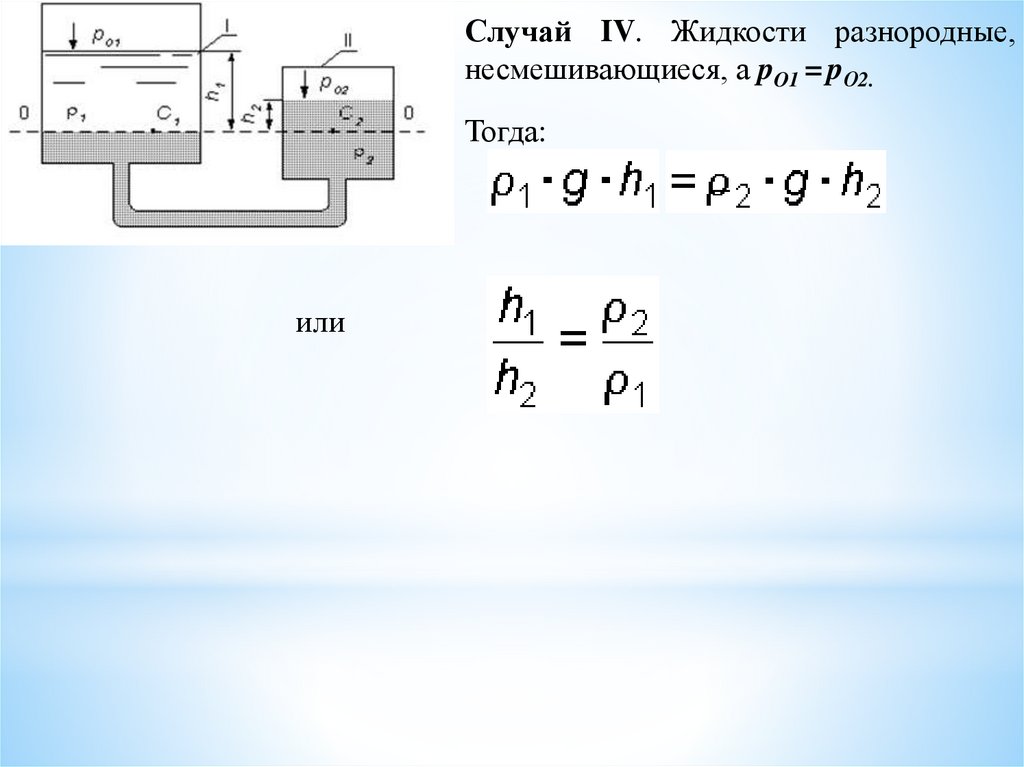
26.

Случай IV. Жидкости разнородные,
несмешивающиеся, а pO1 = pО2.
Тогда:
или

27.

Определение напора
Рассмотрим закрытый сосуд с
жидкостью, к которому в точках А и
В
на
произвольной
глубине
присоединены пьезометры I и II .
Давление на свободной поверхности
в сосуде pO больше атмосферного
pатм. Трубка I сверху открыта и
давление на свободной поверхности
в ней равно атмосферному
Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней
равно нулю Р′′ =0. Для определения вертикальных координат точек А и В
проведем на произвольной высоте горизонтальную плоскость 0-0. Эта
плоскость называется плоскостью сравнения. Вертикальное расстояние
от плоскости сравнения до рассматриваемой точки называется
геометрической высотой точки по отношению к плоскости сравнения и
обозначается буквой . За плоскость сравнения может быть принят
уровень земли, пола.

28.

Так как давление в сосуде на свободной
поверхности
жидкости
больше
атмосферного, то в пьезометрических
трубках I и II жидкость поднимется на
большую высоту, чем уровень жидкости
в сосуде. Обозначим высоту поднятия
жидкости в открытом пьезометре через
hP - пьезометрическая высота, а высоту
поднятия
жидкости
в
закрытом
пьезометре через hпр - приведенная
высота.
Пьезометрическая высота hP - мера манометрического давления в точке А.
Приведенная высота hпр - мера абсолютного давления в точке В. Разность высот
равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10
м.в.ст. Сумма геометрической высоты Z и пьезометрической hP для любой точки
жидкости будет величиной постоянной и называется пьезометрическим напором:

29.

Но
Подставив
формулу
это
выражение
получим
или
это сумма приведенной высоты и геометрической высоты
положения, называемая гидростатическим напором H s
в

30.

Тогда:
В уравнении H s=cons для любой
точки жидкости, а
не зависит от
положения точки.
Значит:
Поэтому, сколько бы мы пьезометров не подключили, во всех
пьезометрах жидкость установится на одном уровне: плоскость,
соответствующая уровню П–П, называется пьезометрической
плоскостью, а уровню Н–Н – напорной плоскостью.

31.

Пьезометрический напор является
мерой удельной потенциальной энергии
жидкости. Предположим, что вес
частицы жидкости в точке А равен G.
По отношении к плоскости сравнения О
– О запас потенциальной энергии
положения равен G ∙ Z, где Z - высота
от плоскости О – О до точки А. Под
действием
избыточного
гидростатического давления pМ частица,
находящаяся на глубине h, может
подняться на высоту hp, то есть она
обладает потенциальной энергией давления равной G ∙ hp. Полная потенциальная
энергия частицы жидкости весом G равна G ∙ Z+ G ∙ hp. Удельная потенциальная
энергия, т.е. энергия приходящаяся на единицу веса частицы будет
соответственно равна:
Аналогично, гидростатический напор H s является также мерой удельной
потенциальной энергии жидкости, но большей по сравнению HP на величину
удельной потенциальной энергии атмосферного давления.

32.

Графическое представление величины и направления гидростатического
давления, действующего на любую точку поверхности, называется эпюрой
давления. Согласно основному уравнению гидростатики, закон распределения
давления по глубине линейный.
Эпюры абсолютного давления и весового давления жидкости без
учета давления на поверхности жидкости.
Эпюры весового давления жидкости без учета давления на
поверхности жидкости.
Эпюры
давления
представляют
соответственно
равномерно распределённую нагрузку в виде трапеции для
абсолютного или полного давления и в виде треугольника для
весового давления. Угол наклона эпюры β зависит от
величины плотности жидкости ρ. Стрелками показано, что
давление в любой точке по глубине действует по внутренней
нормали к поверхности АВ.

33.

Примеры решения задач
Пример 1. Определить абсолютное и избыточное гидростатическое давление
в точке А, расположенной в воде на глубине hA =2,5 м, и пьезометрическую
высоту для точки А, если абсолютное гидростатическое давление на поверхности
р0 =147,2 кПа.
Решение:
Согласно основного уравнения гидростатики абсолютное гидростатическое
давление в точке А определится:
Избыточное давление в точке А равно:
Пьезометрическая высота для точки А
равна:

34.

Можно отметить, что пьезометром удобно
измерять только относительно малые давления,
в противном случае требуется большая высота
пьезометра, что неудобно в эксплуатации.
Определить эти же величины U – образным
манометром,
заполненным
ртутью.
По
поверхности раздела m-n ртути и воды
давления со стороны резервуара и открытого
конца манометра будут одинаковы:
Следовательно, избыточное давление в точке А уравновешивается весом столба
ртути высотой hp над поверхностью раздела m-n:
Находим высоту ртутного столба hp
где ρ рт =13,6 т/м3 - плотность ртути.

35.

Пример 2. Определить давление в резервуаре р0 и высоту подъема уровня h1 в
трубке 1, если показания ртутного манометра h2 = 0,15м, h3 = 0,8м, ρ рт =13,6 т/м3
ρ в =1 т/м3
Решение:
Запишем условия равновесия для ртутного манометра для плоскости
а) со стороны резервуара
б) со стороны манометра
тогда
Таким образом, в резервуаре – вакуум, величина которого равна:
Условия равновесия трубки 1:

36.

Пример 3. Определить манометрическое давление в трубопроводе А,
если высота столба ртути по пьезометру h2 = 25 см. Центр трубопровода
расположен на h1 = 40 см ниже линии раздела между водой и ртутью.
Решение: Находим давление в точке В. Точка В расположена выше точки А на
величину h1, следовательно, давление в точке В будет равно:
В точке С давление будет такое же, как в точке В, то есть
Определим давление в точке C, подходя, справа
Приравнивая оба уравнения, получаем
Отсюда манометрическое давление