Связные графы. Компоненты связности. Понятие связности

1.

3.5. Связные графы.
Компоненты связности
3.5.1. Понятие связности

2.

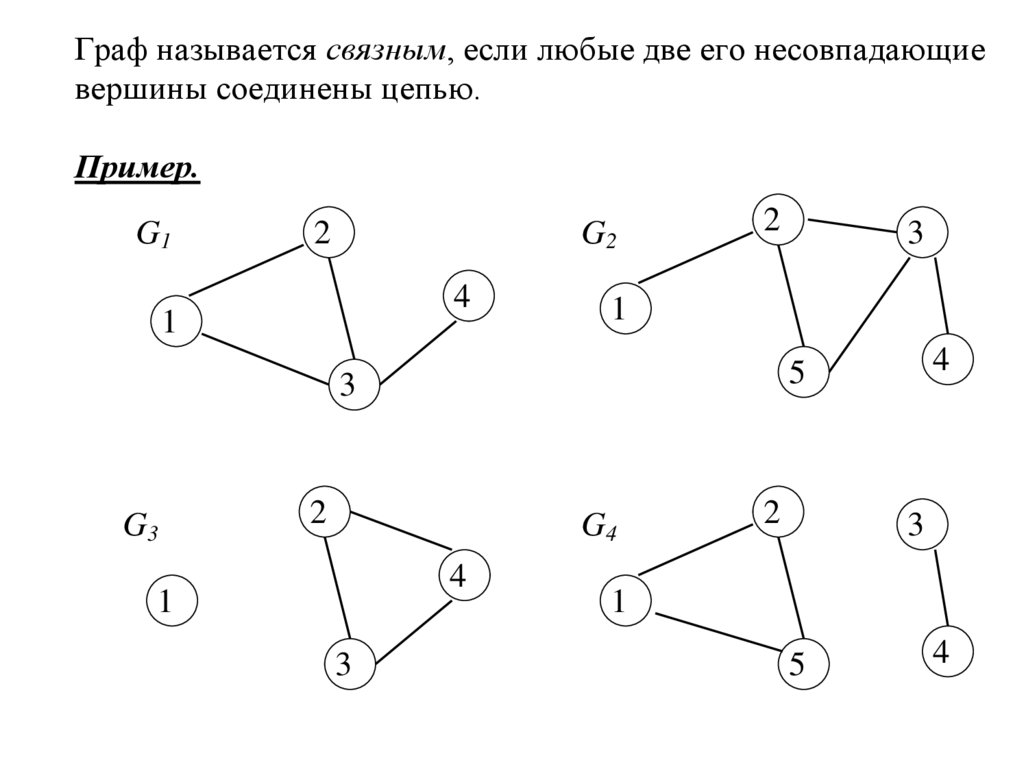
Граф называется связным, если любые две его несовпадающие
вершины соединены цепью.
Пример.
G1
2
G2
4
1
2
1
2
G4
4
1
3
4
5
3
G3
3
2
3
1
5
4

3.

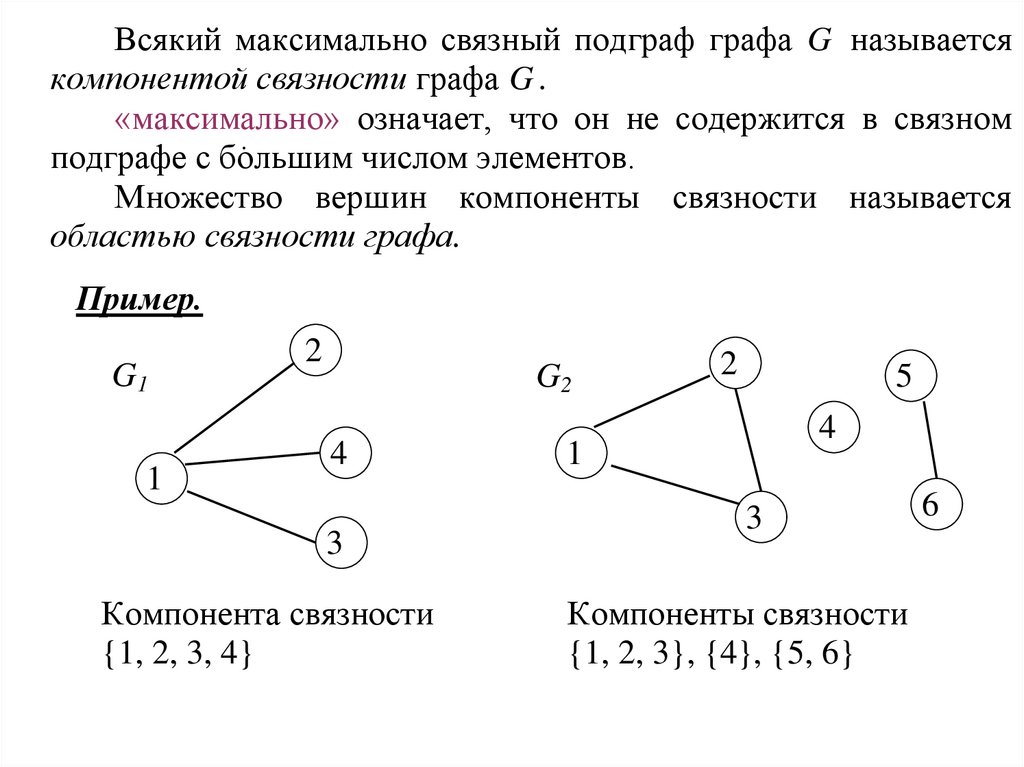
Всякий максимально связный подграф графа G называется
компонентой связности графа G .
«максимально» означает, что он не содержится в связном
подграфе с бȯльшим числом элементов.
Множество вершин компоненты связности называется
областью связности графа.
Пример.
G1
1
2
G2
4
3
Компонента связности
{1, 2, 3, 4}
2
5
4
1
3
Компоненты связности
{1, 2, 3}, {4}, {5, 6}
6

4.

Теорема 3.1. Для любого графа либо он сам, либо его
дополнение является связным.
Теорема 3.2. Пусть G – связный граф, e EG . Тогда
1) если ребро e принадлежит какому-нибудь циклу графа G ,
то граф G e связен;
2) если ребро e не входит ни в один цикл, то граф G e
имеет ровно две компоненты.
Теорема 3.3. (О числе ребер в графе) Если число компонент
связности графа G равно k , то
(n k )(n k 1)
n k m
2
где т – число ребер, n – порядок графа G.

5.

3.5.2. Вершинная
и
реберная связность

6.

Числом вершинной связности κ(G) (каппа)
графа G
называется наименьшее число вершин, удаление которых
приводит к несвязному или одновершинному графу. Если граф
несвязный, то κ(G) = 0.
Пример.
G1
4
1
3
2
G1 – 3
5
6
1
4
5
2
6
κ(G1) = 1

7.

G2
4
1
3
2
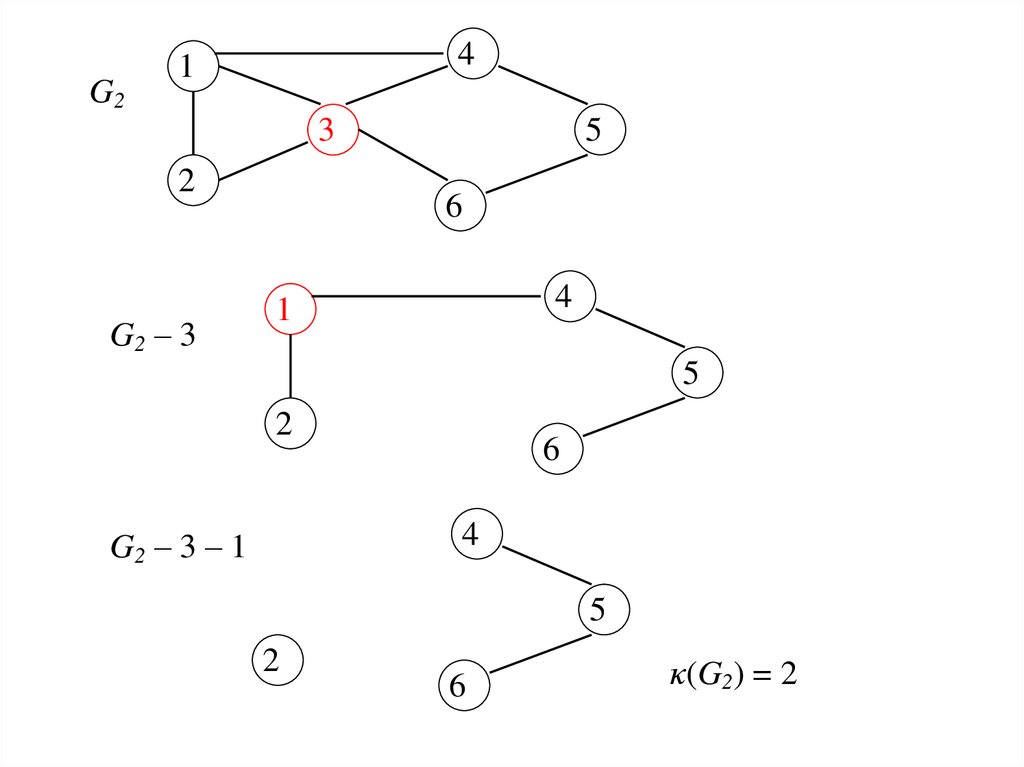
G2 – 3
5
6
4
1
5
2
6
4
G2 – 3 – 1
5
2
6
κ(G2) = 2

8.

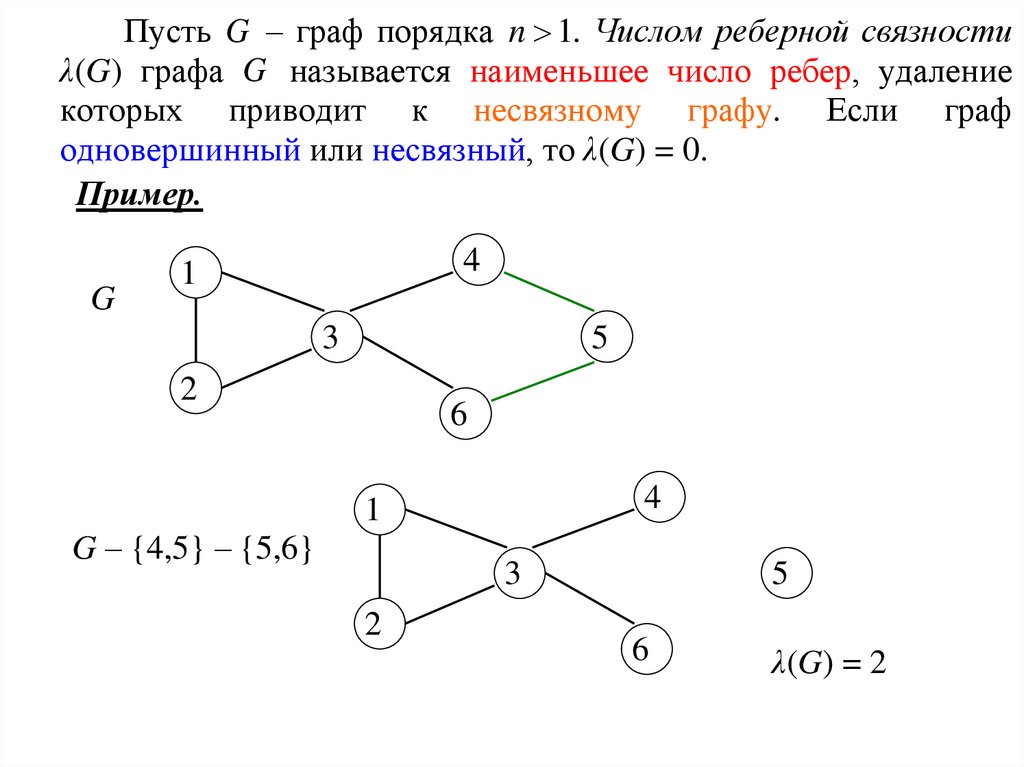
Пусть G – граф порядка n 1. Числом реберной связности
λ(G) графа G называется наименьшее число ребер, удаление
которых приводит к несвязному графу. Если граф
одновершинный или несвязный, то λ(G) = 0.
Пример.
G
4
1
3
5
2
6
4
1
G – {4,5} – {5,6}
3
2
5
6
λ(G) = 2

9.

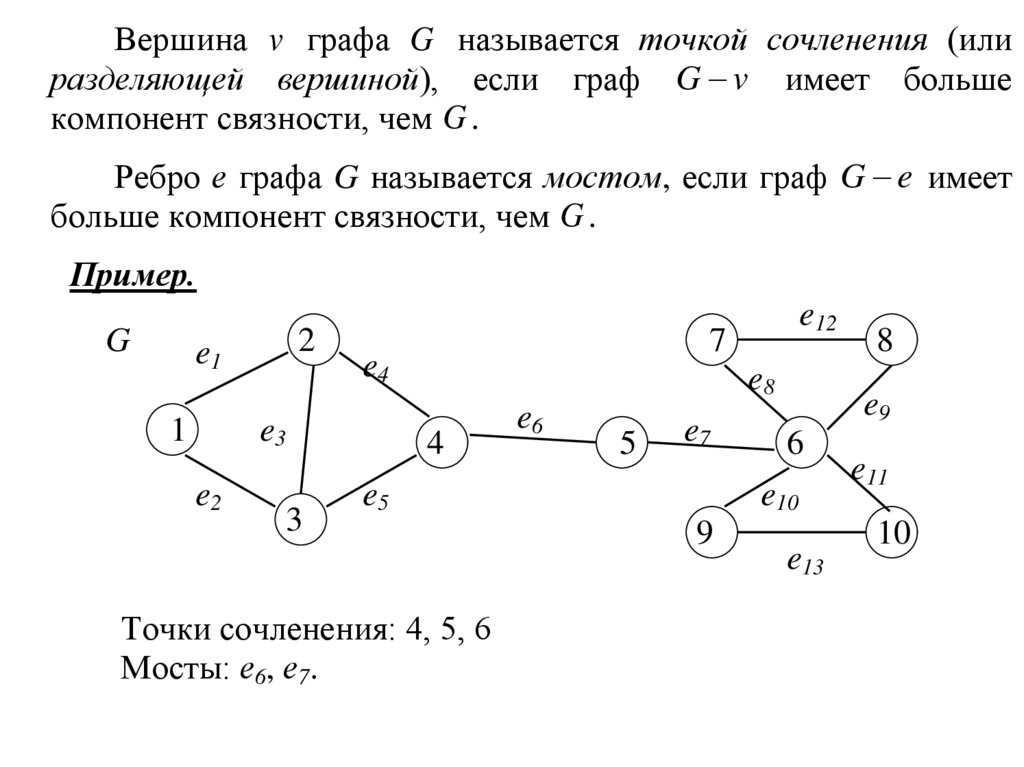
Вершина v графа G называется точкой сочленения (или
разделяющей вершиной), если граф G v имеет больше
компонент связности, чем G .
Ребро е графа G называется мостом, если граф G e имеет
больше компонент связности, чем G .
Пример.
G
2
e1
e2
3
7
e4
e3
1
e12
e8
4
e6
5
e7
Точки сочленения: 4, 5, 6
Мосты: е6, е7.
e9
6
e10
e5
9
8
e13
e11
10

10.

3.5.3. Двусвязные графы

11.

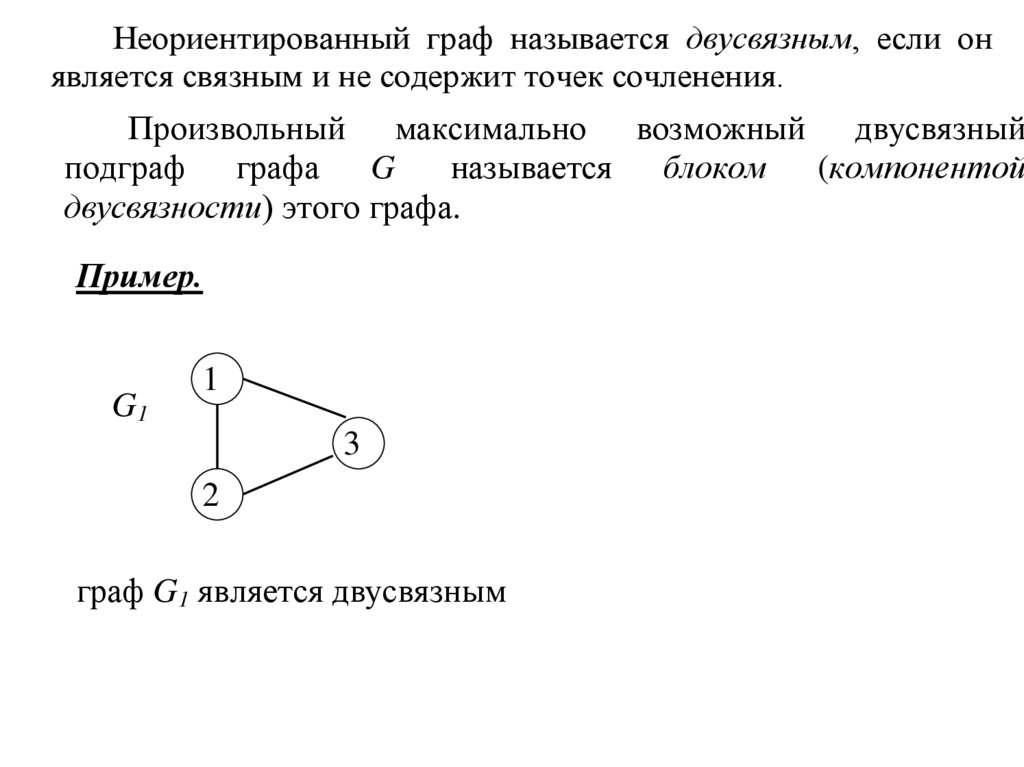
Неориентированный граф называется двусвязным, если он
является связным и не содержит точек сочленения.
Произвольный максимально возможный двусвязный
G
подграф графа
называется блоком (компонентой
двусвязности) этого графа.
Пример.
G1
1
3
2
граф G1 является двусвязным

12.

G2
2
1
4
3
Блоки:
{1, 2, 4, 3}
{5, 6, 7}
{5, 8, 9}
{4, 5}
6
7
5
9
8

13.

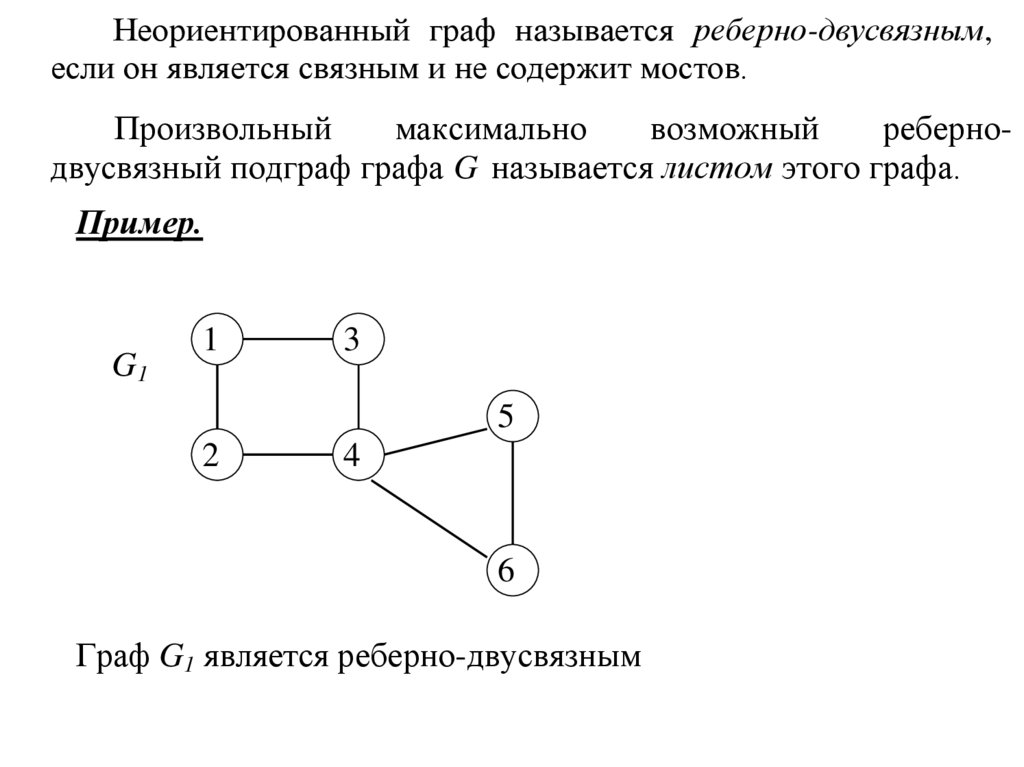
Неориентированный граф называется реберно-двусвязным,
если он является связным и не содержит мостов.
Произвольный
максимально
возможный
ребернодвусвязный подграф графа G называется листом этого графа.
Пример.
G1
1
3
5
2
4
6
Граф G1 является реберно-двусвязным

14.

G2
1
3
8
9
5
2
6
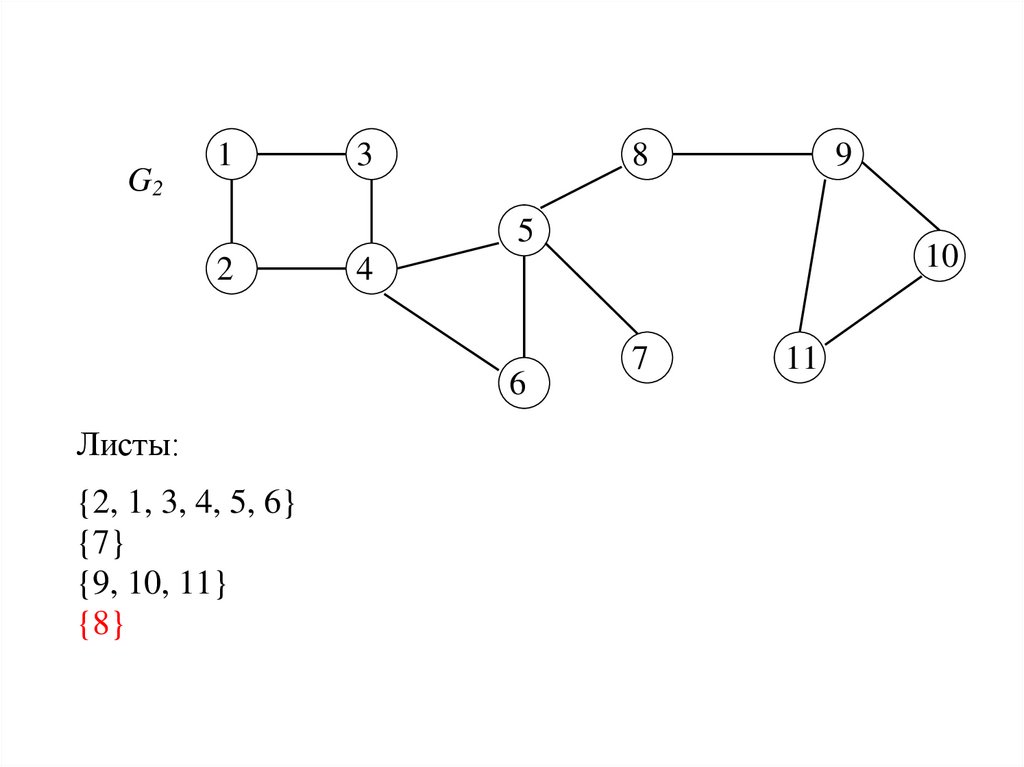
Листы:
{2, 1, 3, 4, 5, 6}
{7}
{9, 10, 11}
{8}
10
4
7
11

15.

3.5.4. Связность в орграфах

16.

Путь в ориентированном графе – ориентированная цепь.
Пусть D(V , А) – орграф, v1 и v2 – его вершины. Тогда
1) две вершины v1 и v2 сильно связаны в орграфе D , если
существует путь из v1 в v2 и из v2 в v1;
2) две вершины v1 и v2 односторонне связаны в орграфе D ,
если существует путь либо из v1 в v2 , либо из v2 в v1;
3) две вершины v1 и v2 слабо связаны в орграфе D , если
они связаны в неориентированном графе G , полученном из
орграфа D путем отмены ориентации дуг.
Сильная связанность влечет одностороннюю связанность,
которая влечет слабую связанность. Обратное неверно.

17.

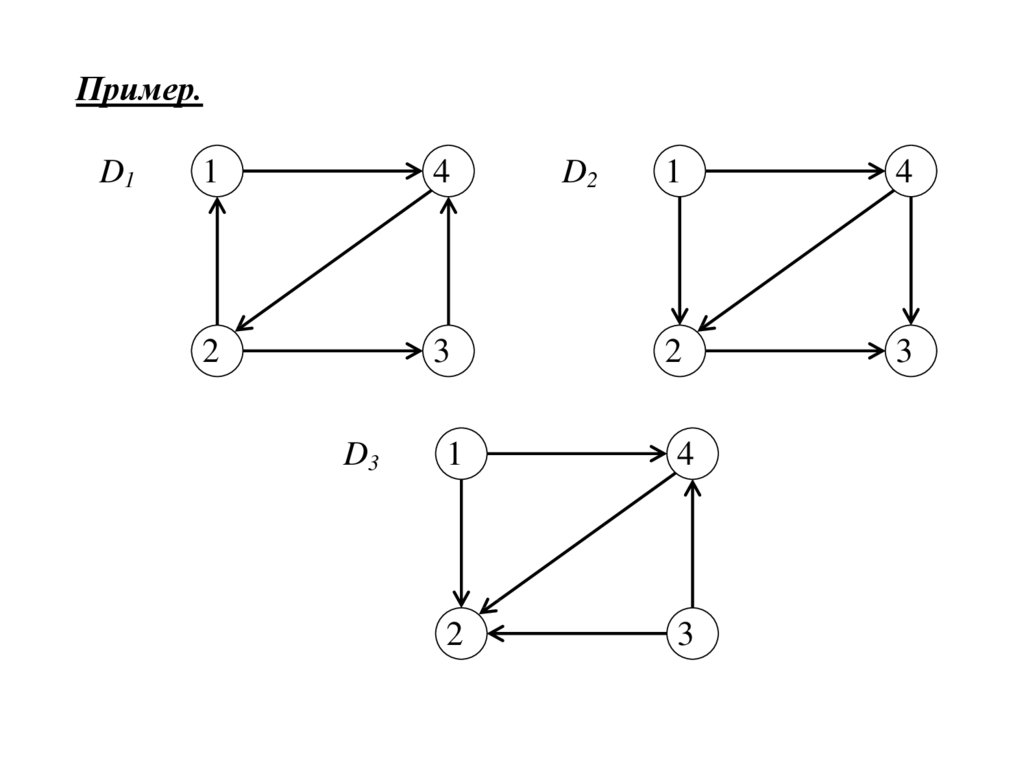
Пример.
D1
1
4
2
3
D3
D2
1
4
2
3
1
4
2
3

18.

Компонента сильной связности (КСС) орграфа D - это его
максимально сильно связный подграф.
Каждая вершина графа принадлежит только одной КСС.
Если вершина не связана с другими, то считается, что она сама
образует КСС.
S – матрица компонент сильной связности (n-го порядка)
1, i j и j i,
sij
0, иначе
главная диагональ матрицы содержит 1.

19.

Пример.
5
1
D
2
4
3
6
7

20.

21.

Компоненты сильной связности:
{1, 3, 5}
{4, 6, 7}
{2}