Похожие презентации:
Системы счисления
1. Системы счисления
ИнновационныйЕвразийский
“ Add your company
slogan ”
Университет
Слайд-лекции по дисциплине
«ИНФОРМАТИКА»
Системы
счисления
www.themegallery.com
Разработала ст.преподаватель Айтуллина Б.А.
LOGO
2. Системы счисления
Основные понятия1
2
3
4
Непозиционные системы
Позиционные системы
Двоичное
кодирование
информации
текстовой
3.
ОпределенияСистема счисления –это знаковая система, в
которой числа записываются по определенным
правилам с помощью символов некоторого
алфавита, называемых цифрами.
Цифры – это знаки, используемые при записи чисел.
Сами знаки составляют алфавит системы
счисления.
4.
ОпределенияСистема счисления – это способ записи чисел
помощью специальных знаков – цифр.
с
Числа:
123, 45678, 1010011, CXL
Цифры:
0, 1, 2, …
I, V, X, L, …
Алфавит – это набор цифр. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Типы систем счисления:
непозиционные – значение цифры не зависит от
ее места (позиции) в записи числа;
позиционные – зависит…
5.
Непозиционные системыУнарная – одна цифра обозначает единицу (1 день,
1 камень, 1 баран, …)
Римская:
I – 1 (палец), V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони), L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)
6.
Римская система счисленияПравила:
(обычно) не ставят больше трех одинаковых
цифр подряд
если младшая цифра (только одна!) стоит слева
от старшей, она вычитается из суммы (частично
непозиционная!)
Примеры:
MDCXLIV =1000+ 500+ 100– 10+ 50– 1+ 5= 1644
2389 = 2000 + 300 + 80 + 9
ММ
ССС
2389 = M M C C C L X X X I X
LXXX
IX
7.
Римская система счисленияПравила:
(обычно) не ставят больше трех одинаковых
цифр подряд
если младшая цифра (только одна!) стоит слева
от старшей, она вычитается из суммы (частично
непозиционная!)
Примеры:
MDCXLIV =1000+ 500+ 100– 10+ 50– 1+ 5= 1644
2389 = 2000 + 300 + 80 + 9
ММ
ССС
2389 = M M C C C L X X X I X
LXXX
IX
8.
Римская система счисленияНедостатки:
для записи больших чисел (>3999) надо вводить
новые знаки-цифры (V, X, L, C, D, M)
как записать дробные числа?
как выполнять арифметические действия:
CCCLIX + CLXXIV =?
Где используется:
номера глав в книгах:
обозначение веков: «Пираты XX века»
циферблат часов
9.
Славянская система счисленияалфавитная система счисления (непозиционная)
10.
Позиционные системыПозиционная система: значение цифры определяется
ее позицией в записи числа.
Десятичная система:
первоначально – счет на пальцах
изобретена в Индии, заимствована арабами, завезена в Европу
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Основание (количество цифр): 10
сотни десятки единицы
2
1
0
3 7 8
300 70
разряды
= 3·102 + 7·101 + 8·100
8
Другие позиционные системы:
• двоичная, восьмеричная, шестнадцатеричная (информатика)
• двенадцатеричная (1 фут = 12 дюймов, 1 шиллинг = 12 пенсов)
• двадцатеричная (1 франк = 20 су)
• шестидесятеричная (1 минута = 60 секунд, 1 час = 60 минут)
10
11.
Перевод целых чиселДвоичная система:
Алфавит: 0, 1
Основание (количество цифр): 2
10 2
19
18
1
2
9
8
1
2
4
4
0
2
2
2
0
2 10
43210
19 = 100112
2
1
0
система
счисления
2
0
1
разряды
100112 = 1·24 + 0·23 + 0·22 + 1·21 + 1·20
= 16 + 2 + 1 = 19
11
12.
Примеры:1010112 =
1101102 =
?
Когда двоичное число четное? делится на 8?
12
13.
Перевод дробных чисел10 2
2 10
0,375 = 0,0112
0,7 = ?
0,7 = 0,101100110…
2
= 0,1(0110)2
0 ,750
0,75
Многие дробные числа нельзя представить в
виде конечных двоичных дробей.
2
1 ,50
Для их точного хранения требуется
бесконечное число разрядов.
0,5
2
Большинство дробных чисел хранится в
1 ,0
памяти с ошибкой.
2-2 =
1
22 = 0,25
2 1 0 -1 -2 -3 разряды
101,0112 = 1·22 + 1·20 + 1·2-2 + 1·2-3
= 4 + 1 + 0,25 + 0,125 = 5,375
14
14.
Примеры:0,625 =
3,875 =
15.
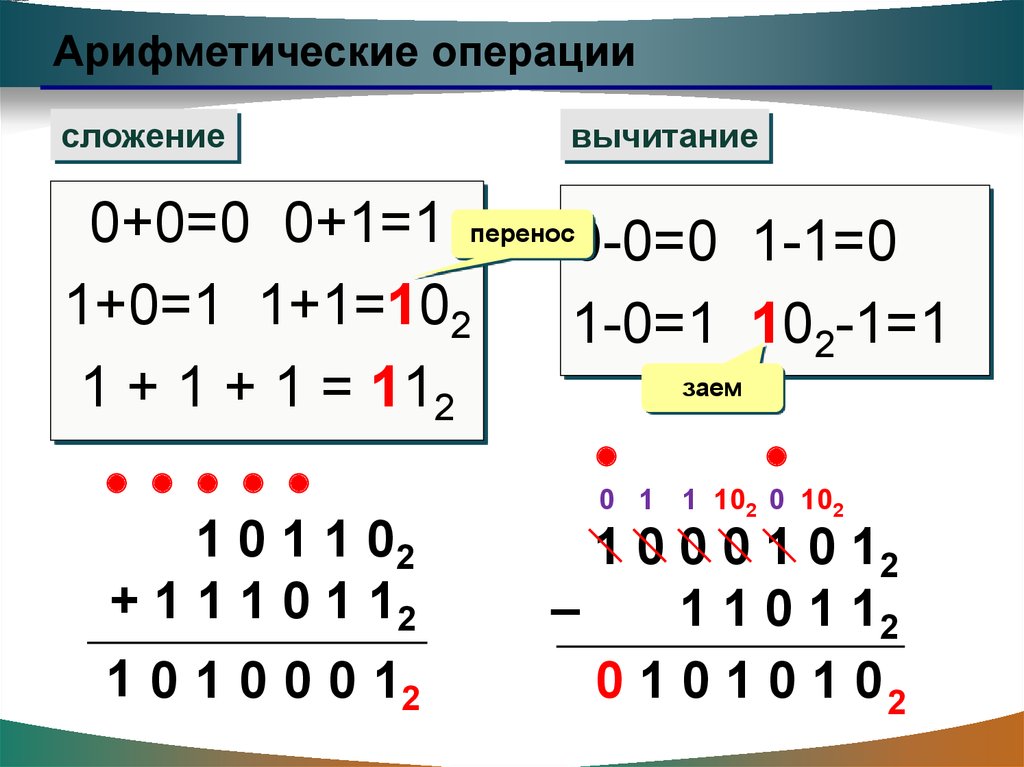
Арифметические операциисложение
вычитание
0+0=0 0+1=1 перенос0-0=0 1-1=0
1+0=1 1+1=102
1-0=1 102-1=1
заем
1 + 1 + 1 = 112
1 0 1 1 02
+ 1 1 1 0 1 12
1 0 1 0 0 0 12
0 1 1 102 0 102
1 0 0 0 1 0 12
–
1 1 0 1 12
0 1 0 1 0 1 02
16.
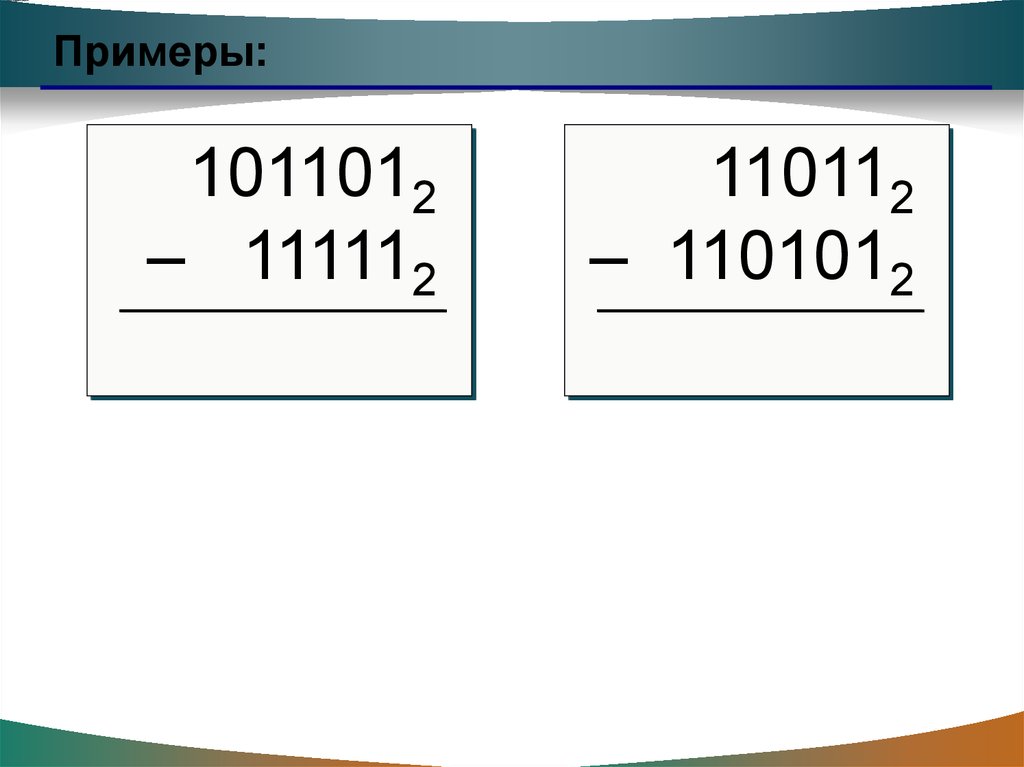
Примеры:1011012
+ 111112
101112
+ 1011102
1110112
+ 110112
1110112
+ 100112
17.
Примеры:1011012
– 111112
110112
– 1101012
18.
Арифметические операцииумножение
1 0 1 0 12
1 0 12
1 0 1 0 12
+ 1 0 1 0 12
1 1 0 1 0 0 12
деление
1 0 1 0 12 1 1 12
– 1 1 12 1 1
2
1 1 12
– 1 1 12
0
19.
Плюсы и минусы двоичной системынужны технические устройства только с двумя
устойчивыми состояниями (есть ток — нет тока,
намагничен — не намагничен и т.п.);
надежность и помехоустойчивость двоичных
кодов;
выполнение операций с двоичными числами для
компьютера намного проще, чем с десятичными.
простые десятичные числа записываются в виде
бесконечных двоичных дробей;
двоичные числа имеют много разрядов;
запись числа в двоичной системе однородна, то
есть содержит только нули и единицы; поэтому
человеку сложно ее воспринимать.
20.
Восьмеричная системаОснование (количество цифр): 8
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
10 8
100 8
96 12 8
8 1
4
4 0
100 = 1448
8
0
система
счисления
1
8 10
210
разряды
1448 = 1·82 + 4·81 + 4·80
= 64 + 32 + 4 = 100
22
21.
Примеры:134 =
75 =
1348 =
758 =
23
22.
Таблица восьмеричных чиселX10
X8
X2
X10
X8
X2
0
0
000
4
4
100
1
1
001
5
5
101
2
2
010
6
6
110
3
3
011
7
7
111
24
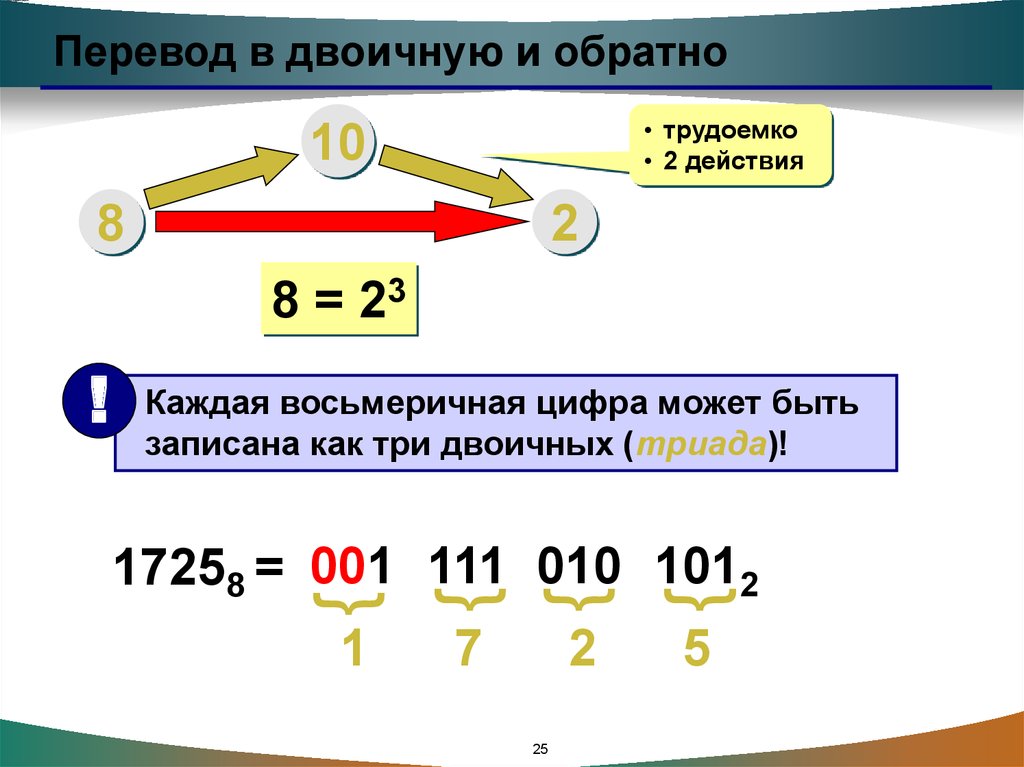
23.
Перевод в двоичную и обратно• трудоемко
• 2 действия
10
8
2
8 = 23
Каждая восьмеричная цифра может быть
записана как три двоичных (триада)!
1
7
2
25
{
{
{
17258 = 001 111 010 1012
{
!
5
24.
Примеры:34678 =
21488 =
73528 =
12318 =
26
25.
Перевод из двоичной системы10010111011112
Шаг 1. Разбить на триады, начиная справа:
001 001 011 101 1112
Шаг 2. Каждую триаду записать одной
восьмеричной цифрой:
001 001 011 101 1112
1
Ответ:
1
3
5
7
10010111011112 = 113578
27
26.
Примеры:1011010100102 =
111111010112 =
11010110102 =
28
27.
Арифметические операциисложение
1 в перенос
1 5 68
+ 6 6 28
1 0 4 08
1 в перенос
6+2=8=8+0
5 + 6 + 1 = 12 = 8 + 4
1+6+1=8=8+0
1 в перенос
29
28.
Пример3 5 38
+ 7 3 68
1 3 5 38
+ 7 7 78
30
29.
Арифметические операциивычитание
заем
4 5 68
– 2 7 78
1 5 78
(6 + 8) – 7 = 7
заем
(5 – 1 + 8) – 7 = 5
(4 – 1) – 2 = 1
31
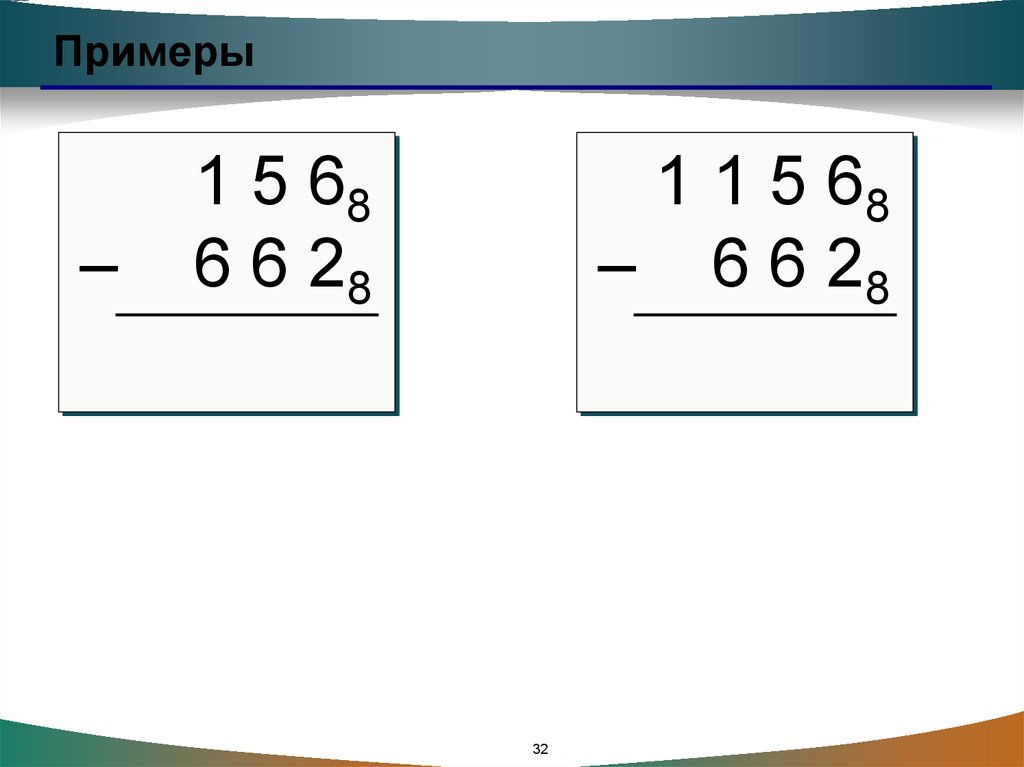
30.
Примеры–
1 5 68
6 6 28
1 1 5 68
– 6 6 28
32
31.
Шестнадцатеричная системаОснование (количество цифр): 16
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
10 11 12 13 14 15
10 16 107 16
96
6 16
107 = 6B16
0 0
11
B
система
6
счисления
16 10
C
1C516 = 1·162 + 12·161 + 5·160
= 256 + 192 + 5 = 453
2 10
разряды
33
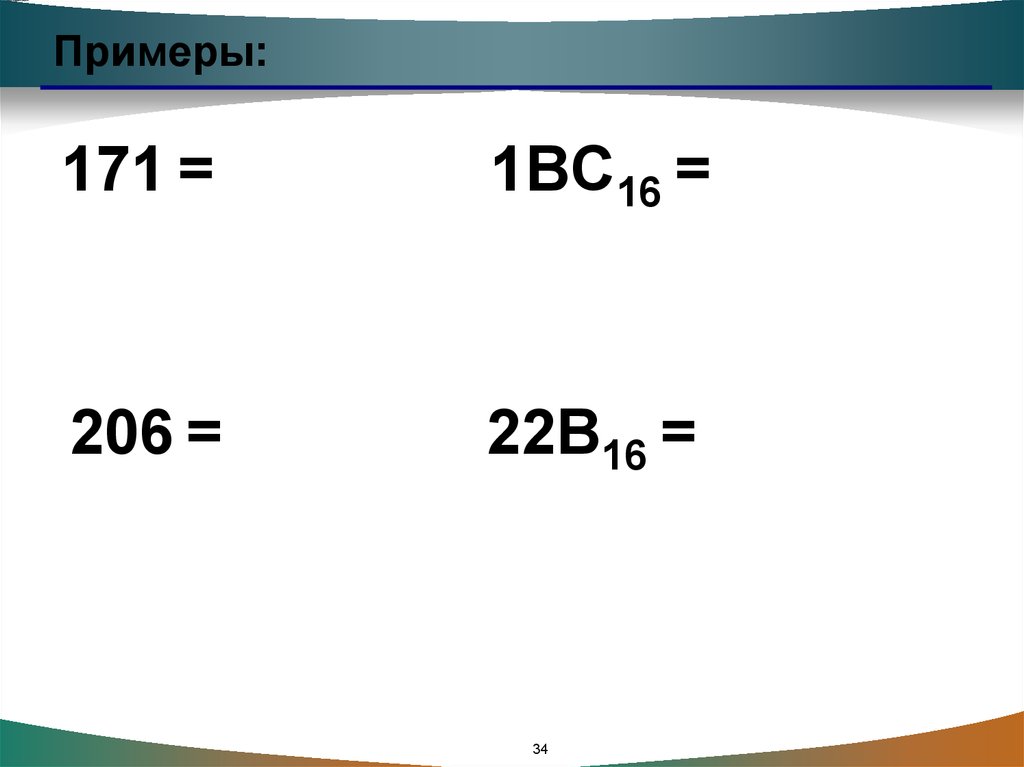
32.
Примеры:171 =
1BC16 =
206 =
22B16 =
34
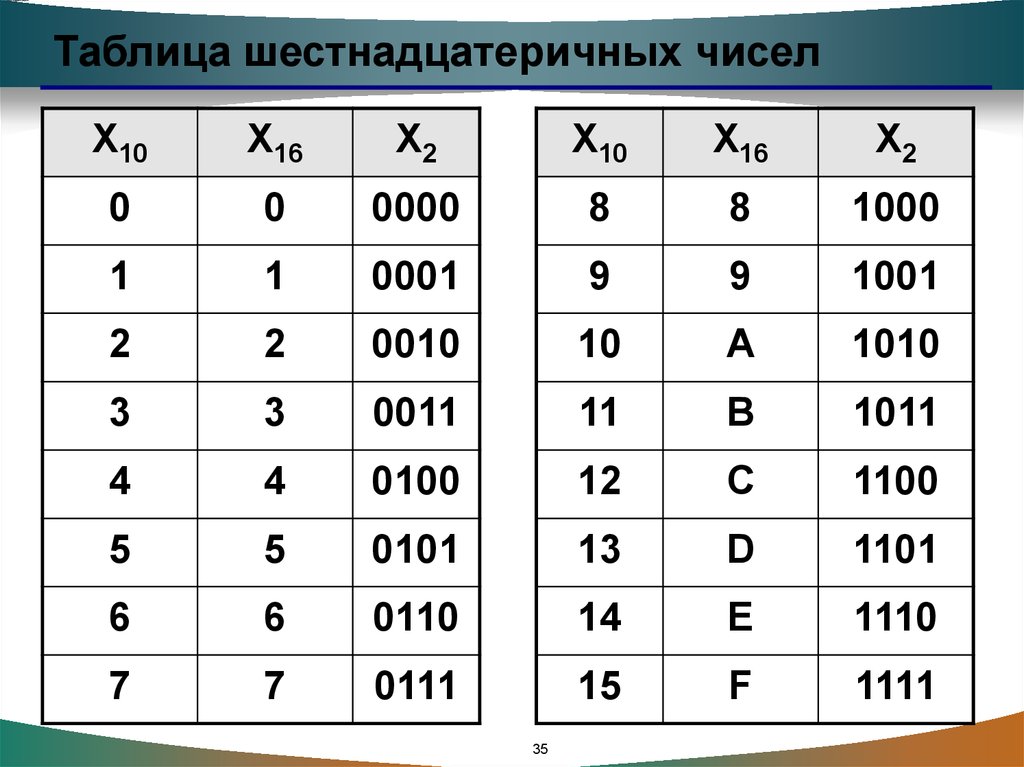
33.
Таблица шестнадцатеричных чиселX10
X16
X2
X10
X16
X2
0
0
0000
8
8
1000
1
1
0001
9
9
1001
2
2
0010
10
A
1010
3
3
0011
11
B
1011
4
4
0100
12
C
1100
5
5
0101
13
D
1101
6
6
0110
14
E
1110
7
7
0111
15
F
1111
35
34.
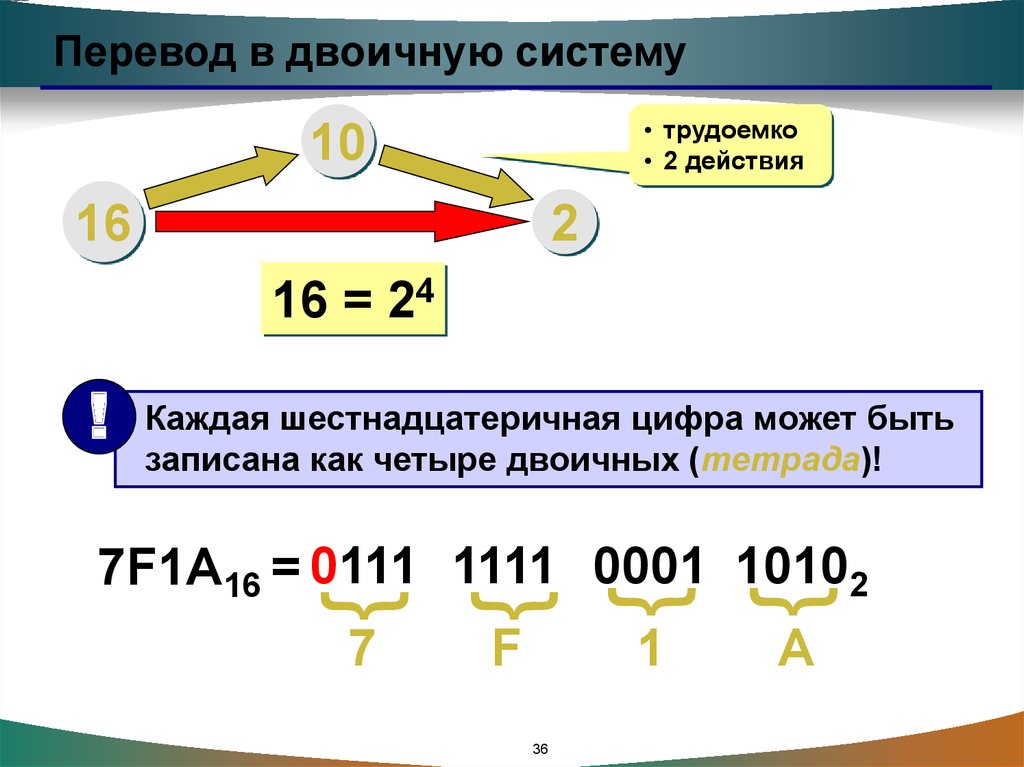
Перевод в двоичную систему• трудоемко
• 2 действия
10
16
2
16 = 24
!
Каждая шестнадцатеричная цифра может быть
записана как четыре двоичных (тетрада)!
7
F
1
36
{
{
{
{
7F1A16 = 0111 1111 0001 10102
A
35.
Примеры:C73B16 =
2FE116 =
37
36.
Перевод из двоичной системы10010111011112
Шаг 1. Разбить на тетрады, начиная справа:
0001 0010 1110 11112
Шаг 2. Каждую тетраду записать одной
шестнадцатеричной цифрой:
0001 0010 1110 11112
1
2
E
F
Ответ:
10010111011112 = 12EF16
38
37.
Примеры:10101011010101102 =
1111001101111101012 =
1101101101011111102 =
39
38.
Перевод в восьмеричную и обратнотрудоемко
10
16
8
2
Шаг 1. Перевести в двоичную систему:
3DEA16 = 11 1101 1110 10102
Шаг 2. Разбить на триады:
011 110 111 101 0102
Шаг 3. Триада – одна восьмеричная цифра:
3DEA16 = 367528
40
39.
Примеры:A3516 =
7658 =
41
40.
Арифметические операциисложение
A 5 B16
+ C 7 E16
1 6 D 916
10 5 11
+ 12 7 14
1 6 13 9
1 в перенос
11+14=25=16+9
5+7+1=13=D16 1 в перенос
10+12=22=16+6
42
41.
Пример:С В А16
+ A 5 916
43
42.
Арифметические операциивычитание
С 5 B16
– A 7 E16
1 D D16
заем
12 5 11
– 10 7 14
1 13 13
заем
(11+16)–14=13=D16
(5 – 1)+16 – 7=13=D16
(12 – 1) – 10 = 1
44
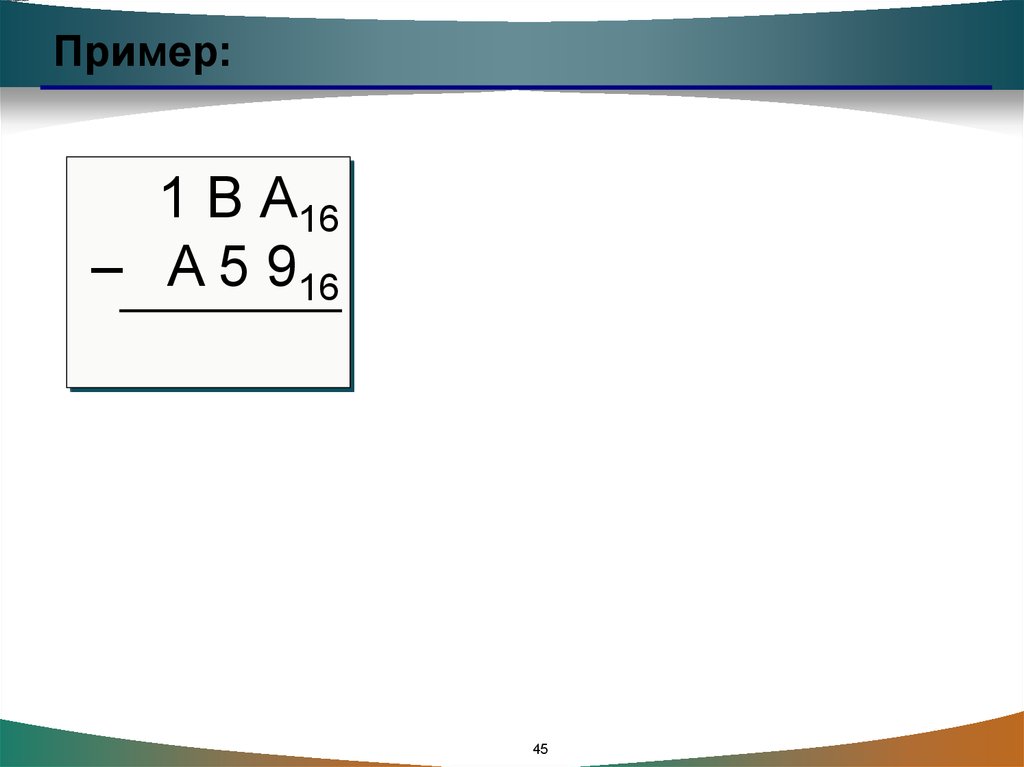
43.
Пример:1 В А16
– A 5 916
45
44.
Троичная уравновешенная системаЗадача Баше:
Найти такой набор из 4 гирь, чтобы с их помощью на
чашечках равноплечных весов можно было взвесить груз
массой от 1 до 40 кг включительно. Гири можно
располагать на любой чашке весов.
46
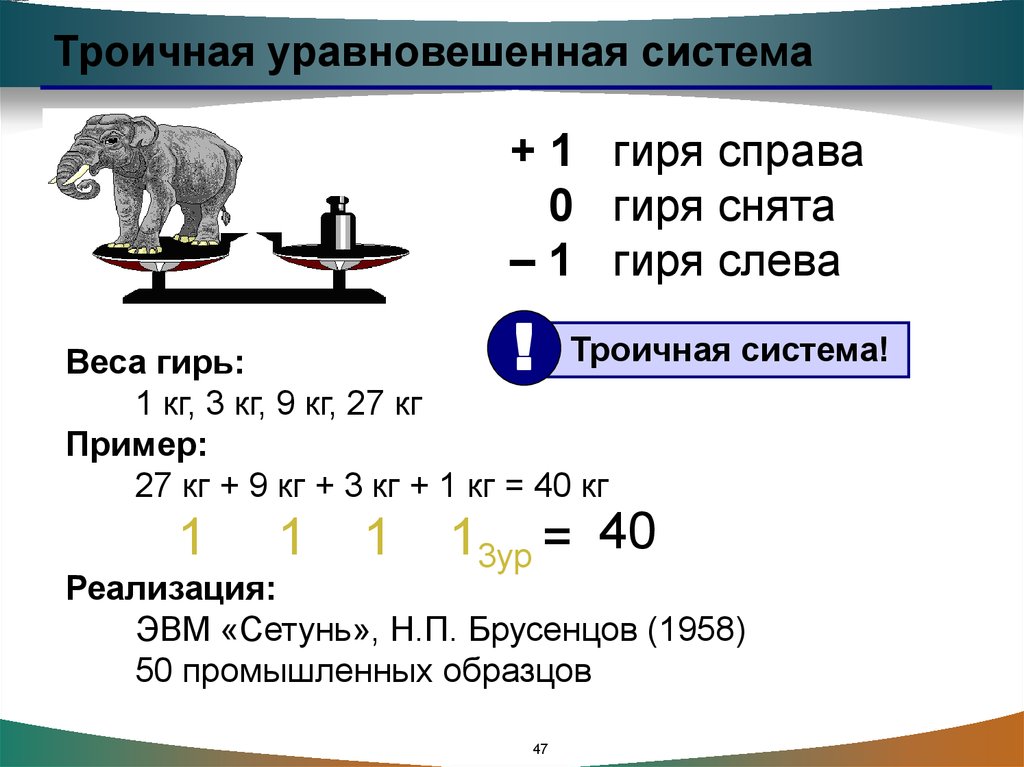
45.
Троичная уравновешенная система+ 1 гиря справа
0 гиря снята
– 1 гиря слева
!
Троичная система!
Веса гирь:
1 кг, 3 кг, 9 кг, 27 кг
Пример:
27 кг + 9 кг + 3 кг + 1 кг = 40 кг
1
1
1
13ур = 40
Реализация:
ЭВМ «Сетунь», Н.П. Брусенцов (1958)
50 промышленных образцов
47
46.
Измерение информацииСодержательный
подход
к
измерению
информации. Сообщение – информативный поток,
который в процессе передачи информации
поступает к приемнику.
Сообщение несет
информацию для человека, если содержащиеся в
нем сведения являются для него новыми и
понятными
Информация - знания человека ?
сообщение должно быть информативно. Если
сообщение не информативно, то количество
информации с точки зрения человека = 0. (Пример:
вузовский учебник по высшей математике содержит
знания, но они не доступны 1-класснику)
48
47.
Измерение информацииАлфавитный подход к измерению информации не
связывает кол-во информации с содержанием
сообщения. Алфавитный подход - объективный
подход к измерению информации. Он удобен при
использовании технических средств работы с
информацией, т.к. не зависит от содержания
сообщения. Кол-во информации зависит от объема
текста и мощности алфавита. Ограничений на max
мощность алфавита нет, но есть достаточный
алфавит мощностью 256 символов. Этот алфавит
используется
для
представления
текстов
в
компьютере. Поскольку 256=28, то 1символ несет в
тексте 8 бит информации.
49
48. Измерение информации
Вероятностный подход к измерения информации. Всесобытия происходят с различной вероятностью,
но
зависимость между вероятностью событий и
количеством информации, полученной при совершении
того или иного события можно выразить формулой
которую в 1948 году предложил Шеннон.
Формула Шеннона
I - количество информации
pi – вероятности отдельных событий
N – количество возможных событий
Количество информации достигает max значения, если
события равновероятны, поэтому количество информации
можно рассчитать по формуле
50
49. Измерение информации
Единицы измерения1 бит (binary digit, двоичная цифра) – это
количество информации, которое мы получаем
при выборе одного из двух возможных
вариантов (вопрос: «Да» или «Нет»?)
51
50. Измерение информации
Единицы измерения1 байт (bytе)
= 8 бит
1 Кб (килобайт) = 1024 байта
1 Мб (мегабайт)
= 1024 Кб
1 Гб (гигабайт) = 1024 Мб
1 Тб (терабайт) = 1024 Гб
1 Пб (петабайт) = 1024 Тб
210
52
51. Единицы измерения
Информационный вес символа произвольного алфавитаИнформационный вес символа алфавита i и
мощность алфавита N связаны между собой
соотношением: N = 2i.
Информационный
объём
сообщения
Информационный объём сообщения (количество
информации
в
сообщении),
представленного
символами естественного или формального языка,
складывается
из
информационных
весов
составляющих
его
символов.
Информационный объём сообщения l равен
произведению
количества
символов
в
сообщении K на информационный вес
символа алфавита i;
l = K * i.
53
52. Единицы измерения
Информационный вес символа произвольного алфавитаЗадача. Сообщение, записанное буквами 32символьного алфавита, содержит 140
символов. Какое количество информации оно
несёт?
Решение.
N = 32
К = 140
I-?
I=К*i
N = 2i
32 = 2i, i = 5,
I = 140 * 5 = 700 (битов)
Ответ: 700 битов.
54
53. Информационный вес символа произвольного алфавита
Задача. Информационное сообщение объёмом720 битов состоит из 180 символов. Какова
мощность алфавита, с помощью которого
записано это сообщение?
Решение.
I = 720
К = 180
N-?
N = 2i,
I = K * i,
i=I/K
i = 720 / 180 = 4 (бита)
N = 24 = 16(символов)
Ответ: 16 символов.
55
54. Информационный вес символа произвольного алфавита
Задача. Информационное сообщение объёмом 4Кбайта состоит из 4096 символов. Каков
информационный вес символа используемого
алфавита? Сколько символов содержит алфавит, с
помощью которого записано это сообщение?
Решение.
I = 4 Кб
К = 4096
i-?
N -?
I = 4 Кб = 4 * 1024 * 8 битов
N = 2i
I=К*i
i=I/К
i = 4 * 1024 * 8 / 4096 = 8 битов
N = 28 = 256 символов
Ответ: 8 битов, 256 символов.
56
55.
Кодирование текстовой информацииCначала применялась 7-битная кодировка,
которая могла представить 128 символов.
С
распространением
IBM
PC
международным стандартом стала
таблица кодировки ASCII (American
Standart Code for Information Interchange)
– Американский стандартный код для
информационного
обмена.таблицы
Кодовые
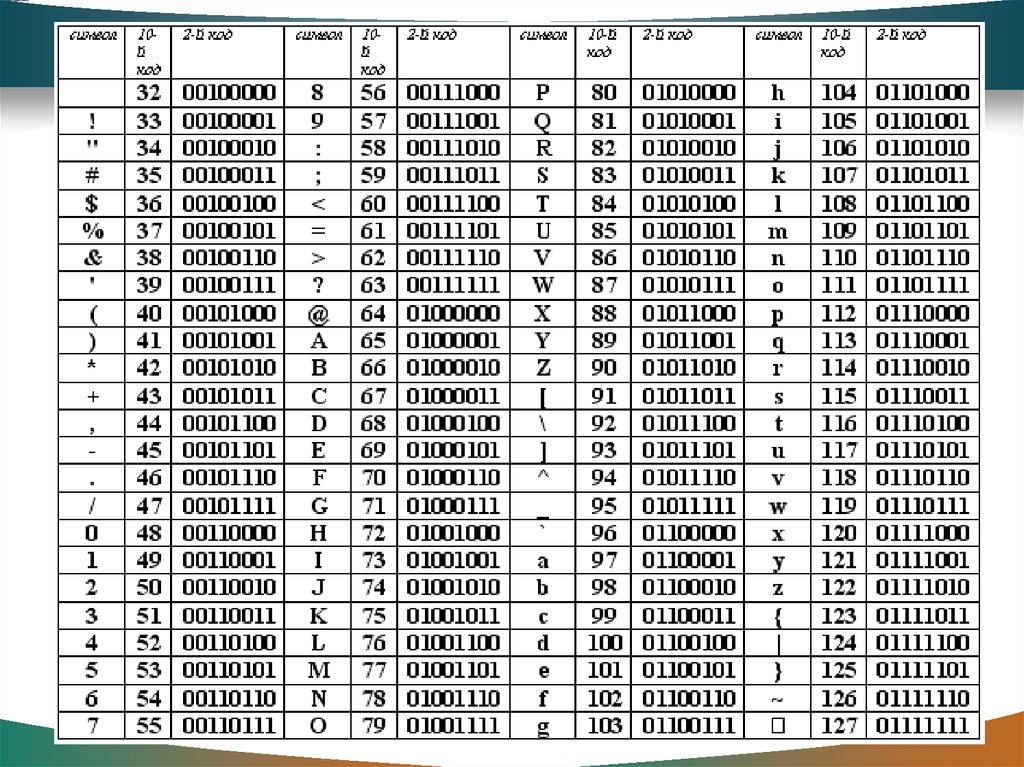
56.
Таблица кодировки ASCIIПозже она была расширена до 8 бит (256
символов) и дошла в таком виде практически
до сегодняшнего дня. При этом первая
половина (символы 0-127) были всегда одни и
те же, соответствующие стандарту ASCII,
а вторая половина таблицы (символы 128255) менялась в зависимости от страны, где
она использовалась.
57. Кодовые таблицы
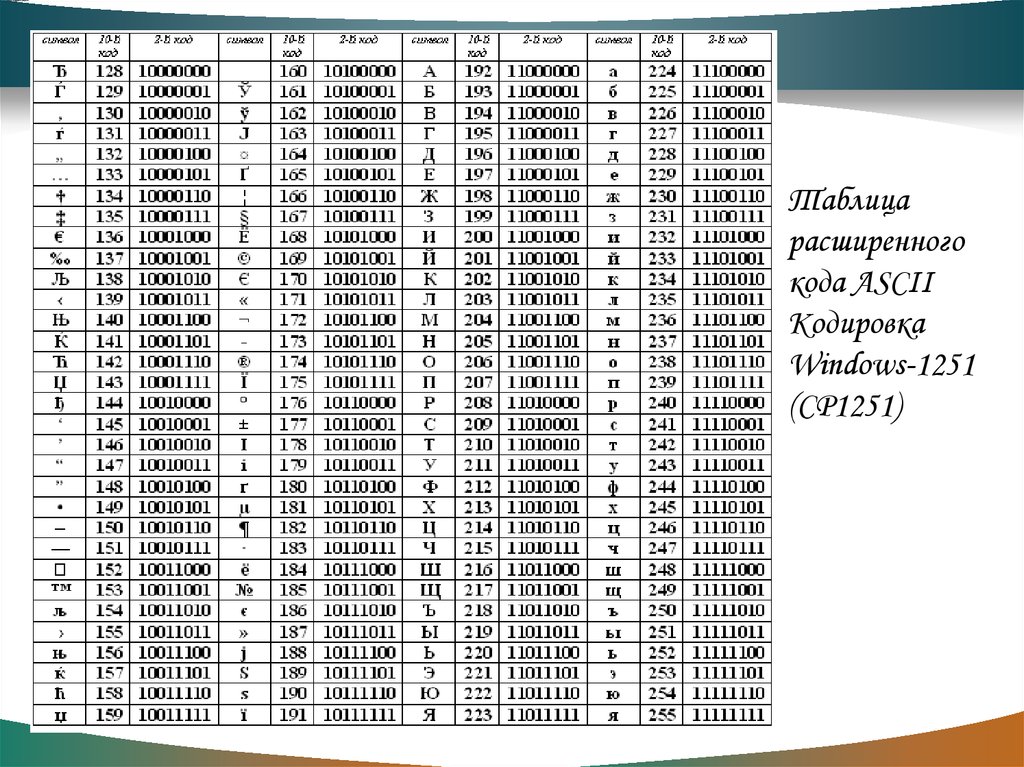
Стандартная часть таблицы58. Таблица кодировки ASCII
Таблицарасширенного
кода ASCII
Кодировка
Windows-1251
(CP1251)
59.
Кодовые таблицы для русских буквВ настоящее время существует 5 разных
кодовых таблиц для русских букв (КОИ8, СР1251,
СР866, Mac, ISO).
Широкое распространение получил новый
международный стандарт Unicode, который
отводит на каждый символ два байта. С его
помощью можно закодировать 65536 (216= 65536)
различных символов.
60.
Кодовые таблицыВ Советском Союзе различные организации
и сети, имевшие большое влияние на
компьютерный и программный рынок тех
времен, создавали свои кодировки (т.е.
вторые половины таблицы), содержащие
русские символы.
61. Кодовые таблицы для русских букв
Проблемы с кодировкамиПроблемы с кодировками делятся
на несколько типов. Первый тип это отсутствие информации о
кодировке.
62. Кодовые таблицы
Проблемы с кодировкамиПроблемы второго типа - это
когда кодировка в файле указана, но
конечная
программа
такой
кодировки не знает.
63. Проблемы с кодировками
Третий тип проблем, наоборот,связан с избытком информации о
кодировках.
Это актуальная в настоящее время
проблема (например, для вебстраниц).
64. Проблемы с кодировками
Обратите внимание!Цифры кодируются по стандарту ASCII в
двух случаях – при вводе-выводе и когда они
встречаются в тексте. Если цифры
участвуют в вычислениях, то осуществляется
их преобразование в другой двоичных код.
65. Проблемы с кодировками
Возьмем число 57.При использовании в тексте каждая
цифра будет представлена своим кодом в
соответствии с таблицей ASCII. В двоичной
системе это – 0011010100110111.
При использовании в вычислениях, код
этого числа будет получен по правилам
перевода в двоичную систему и получим –
00111001.
Обратите внимание!
66. Обратите внимание!
Компьютерные редакторы, в основном,работают с алфавитом размером 256
символов.
В этом случае легко подсчитать объем
информации в тексте. Если 1 символ
алфавита несет 1 байт информации, то надо
просто сосчитать количество символов;
полученное число даст информационный
объем текста в байтах.
67. Обратите внимание!
I=K×i, гдеI-информационный объем сообщения
K- количество символов в тексте
i- информационный вес одного символа
i
2=
N
N- мощность алфавита
Формулы для расчета информационного объема текста
68.
Задачи: текстСколько места в памяти надо выделить для
хранение предложения
Привет, друг!
считаем все символы, включая знаки
препинания (здесь 13 символов)
если нет дополнительной информации, то
считаем, что 1 символ занимает 1 байт
в кодировке UNICODE 1 символ занимает
2 байта
Ответ: 13 байт или 104 бита
(в UNICODE: 26 байт или 208 бит)
70
69. Формулы для расчета информационного объема текста
Задачи: текстСколько места надо выделить для хранения
10 страниц книги, если на каждой странице
помещаются 32 строки по 64 символа в
каждой?
Решение:
на 1 странице 32·64=2048 символов
на 10 страницах 10·2048=20480 символов
каждый символ занимает 1 байт
Ответ:
20480 байт или …
20480·8 бит или …
20480:1024 Кб = 20 Кб
71
70. Задачи: текст
Задачи: рисунокДля хранения растрового рисунка размером
32х64
пикселя
выделили
2 Кб памяти. Каково максимально возможное
количество цветов в палитре?
Решение:
общее число пикселей: 32·64=25 · 26=211
память
2 Кб =2 · 210 байта = 211 байта= 214 бита
на 1 пиксель приходится
214:211 = 23 = 8 бит
8 бит выбор 1 из 256 вариантов
Ответ:
не более 256 цветов
74
71. Задачи: текст
Задачи: рисунокСколько места в памяти надо выделить для
хранения 16-цветного рисунка размером 32 на
64 пикселя?
Решение:
общее число пикселей: 32·64=2048
при
использовании
16
на
1
пиксель
отводится
(выбор 1 из 16 вариантов)
Ответ:
2048·4 бита = 8192 бита или …
2048·4:8 байта = 1024 байта или …
1024:1024 Кб = 1 Кб
75
цветов
4
бита
72. Задачи: кодирование
“ Add your company slogan ”LOGO


















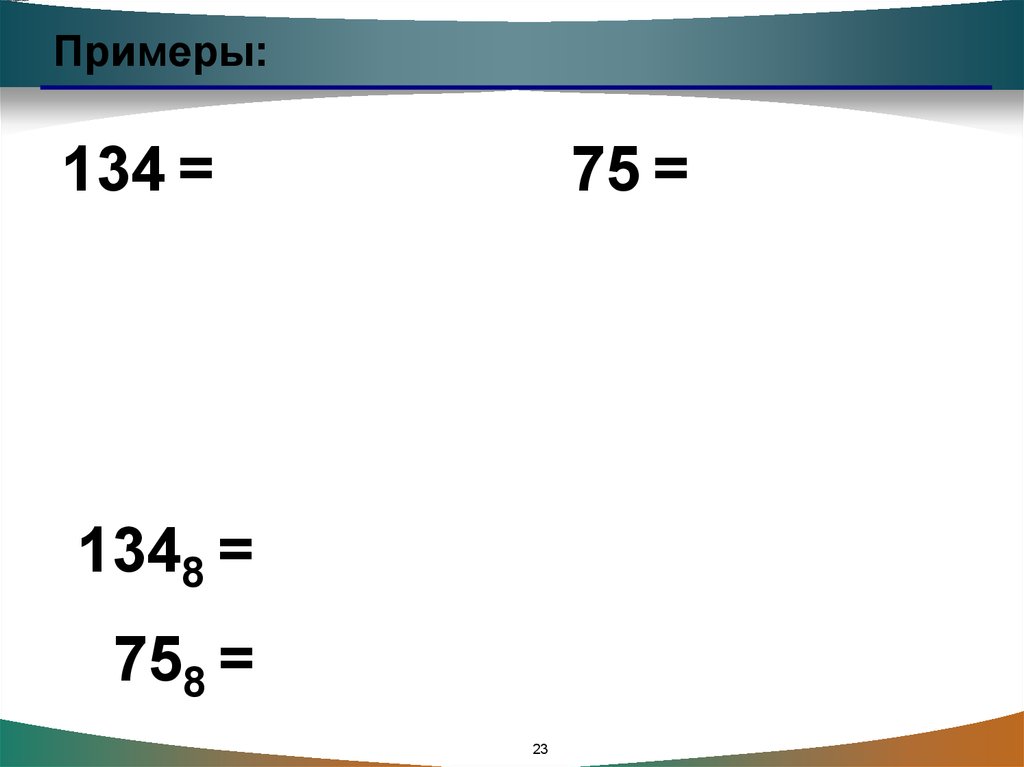










































 Информатика
Информатика