Похожие презентации:
Умножение и деление обыкновенных дробей
1.
2.
а) (2; - 1); (2; 2); (2; 10)у
б) (- 7; 2); (4; 2); (15; 2)
в) (- 2; - 1,5); (- 2; 0); (- 2; 111)
г) (- 2,3; - 2); (5; - 2); (1129; - 2)
0
1
х
3.
а) (1; - 1); (5; 2); (6; 10)у
б) (- 7; 8); (4; 23); (15; 2)
в) (- 1; - 1,5); (- 7; 0); (- 11; 111)
г) (- 2,3; - 1); (5; - 2); (1129; - 3)
0
1
х
4.
Машинистка2
t
I
5ч
II
10 ч
2
1
3
1 1
+
=
+
=
5 10 10 10 10
v
1
5
1
10
А
1 рук.
1 рук.
5.
05.12.2018Классная
р а б о т а.
6.
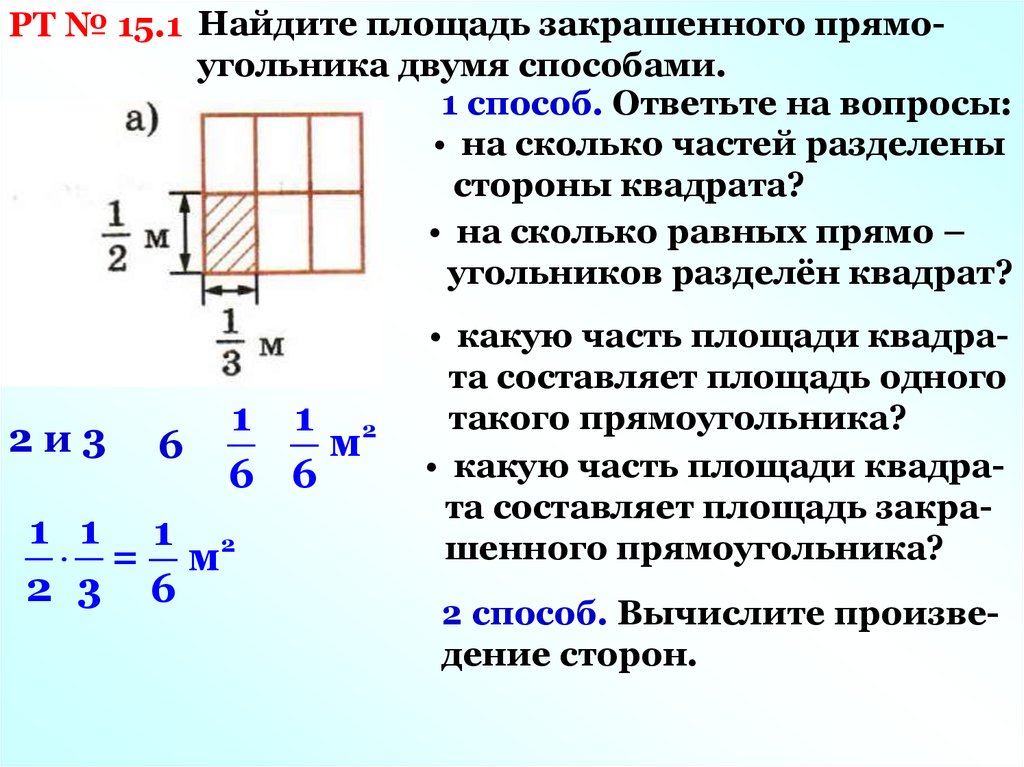
РТ № 15.1 Найдите площадь закрашенного прямоугольника двумя способами.1 способ. Ответьте на вопросы:
• на сколько частей разделены
стороны квадрата?
• на сколько равных прямо –
угольников разделён квадрат?
2и3
6
1 1 2
м
6 6
1 1 1 2
= м
2 3 6
• какую часть площади квадрата составляет площадь одного
такого прямоугольника?
• какую часть площади квадрата составляет площадь закрашенного прямоугольника?
2 способ. Вычислите произведение сторон.
7.
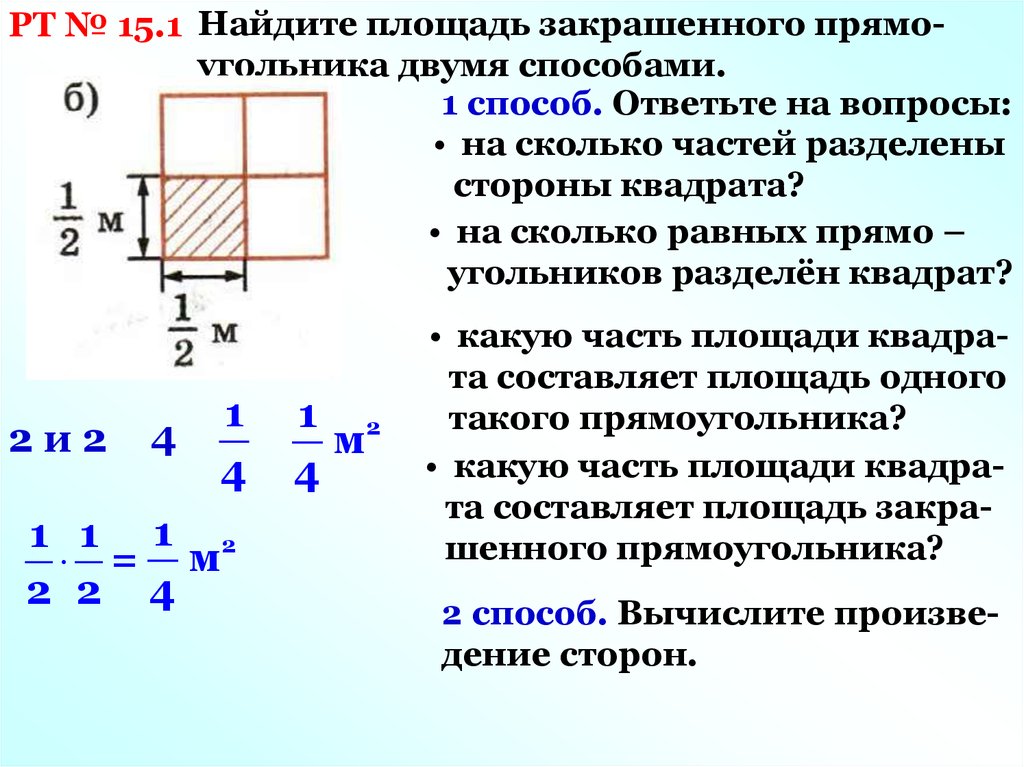
РТ № 15.1 Найдите площадь закрашенного прямоугольника двумя способами.1 способ. Ответьте на вопросы:
• на сколько частей разделены
стороны квадрата?
• на сколько равных прямо –
угольников разделён квадрат?
2и2
4
1
4
1 1 1 2
= м
2 2 4
1 2
м
4
• какую часть площади квадрата составляет площадь одного
такого прямоугольника?
• какую часть площади квадрата составляет площадь закрашенного прямоугольника?
2 способ. Вычислите произведение сторон.
8.
РТ № 15.1 Найдите площадь закрашенного прямоугольника двумя способами.1 способ. Ответьте на вопросы:
• на сколько частей разделены
стороны квадрата?
• на сколько равных прямо –
угольников разделён квадрат?
3и3
9
1
9
1 1 1 2
= м
3 3 9
1 2
м
9
• какую часть площади квадрата составляет площадь одного
такого прямоугольника?
• какую часть площади квадрата составляет площадь закрашенного прямоугольника?
2 способ. Вычислите произведение сторон.
9.
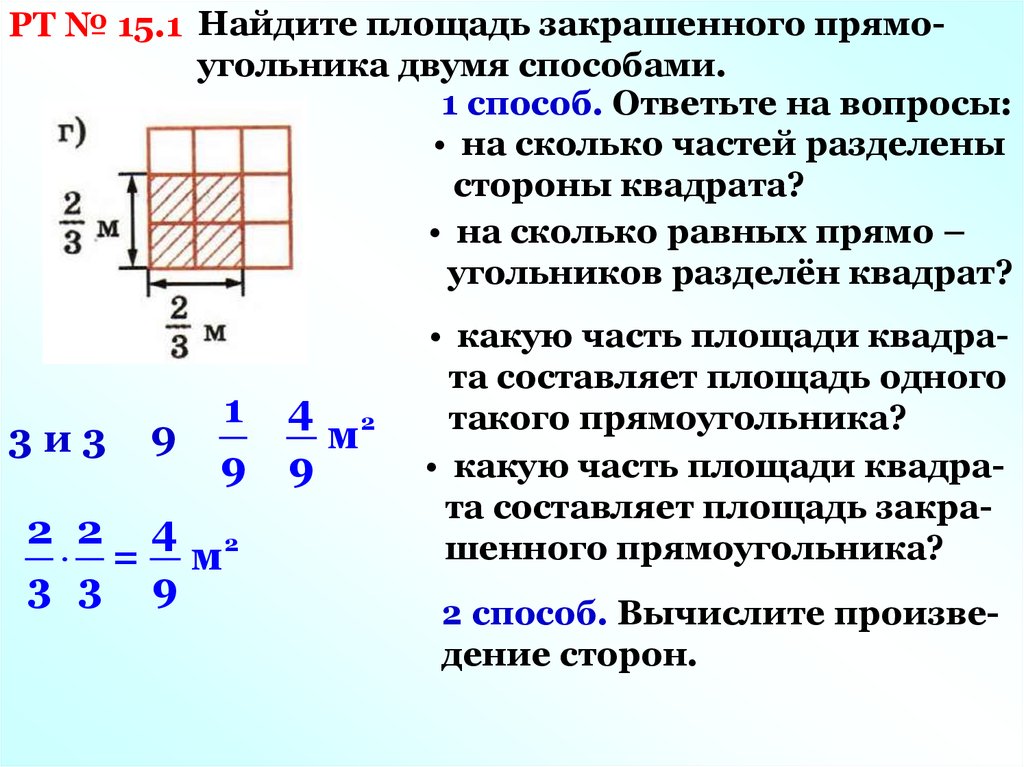
РТ № 15.1 Найдите площадь закрашенного прямоугольника двумя способами.1 способ. Ответьте на вопросы:
• на сколько частей разделены
стороны квадрата?
• на сколько равных прямо –
угольников разделён квадрат?
3и3
9
1
9
2 2 4 2
= м
3 3 9
4 2
м
9
• какую часть площади квадрата составляет площадь одного
такого прямоугольника?
• какую часть площади квадрата составляет площадь закрашенного прямоугольника?
2 способ. Вычислите произведение сторон.
10.
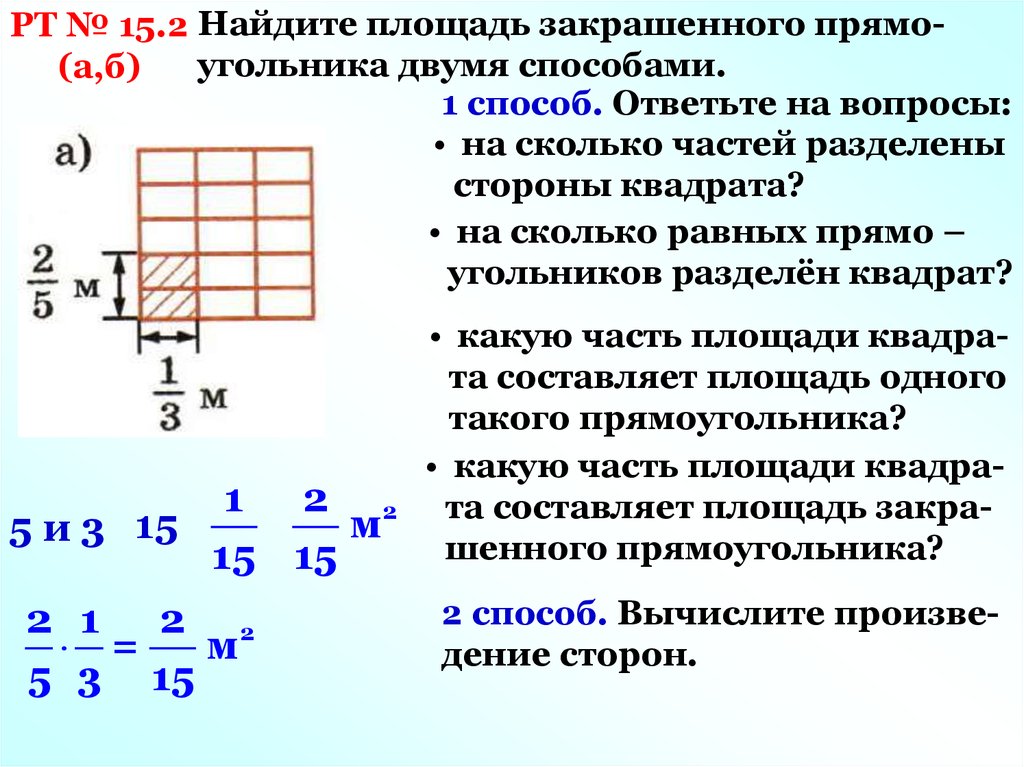
РТ № 15.2 Найдите площадь закрашенного прямоугольника двумя способами.(а,б)
1 способ. Ответьте на вопросы:
• на сколько частей разделены
стороны квадрата?
• на сколько равных прямо –
угольников разделён квадрат?
1 2 2
м
5 и 3 15
15 15
2 1 2 2
=
м
5 3 15
• какую часть площади квадрата составляет площадь одного
такого прямоугольника?
• какую часть площади квадрата составляет площадь закрашенного прямоугольника?
2 способ. Вычислите произведение сторон.
11.
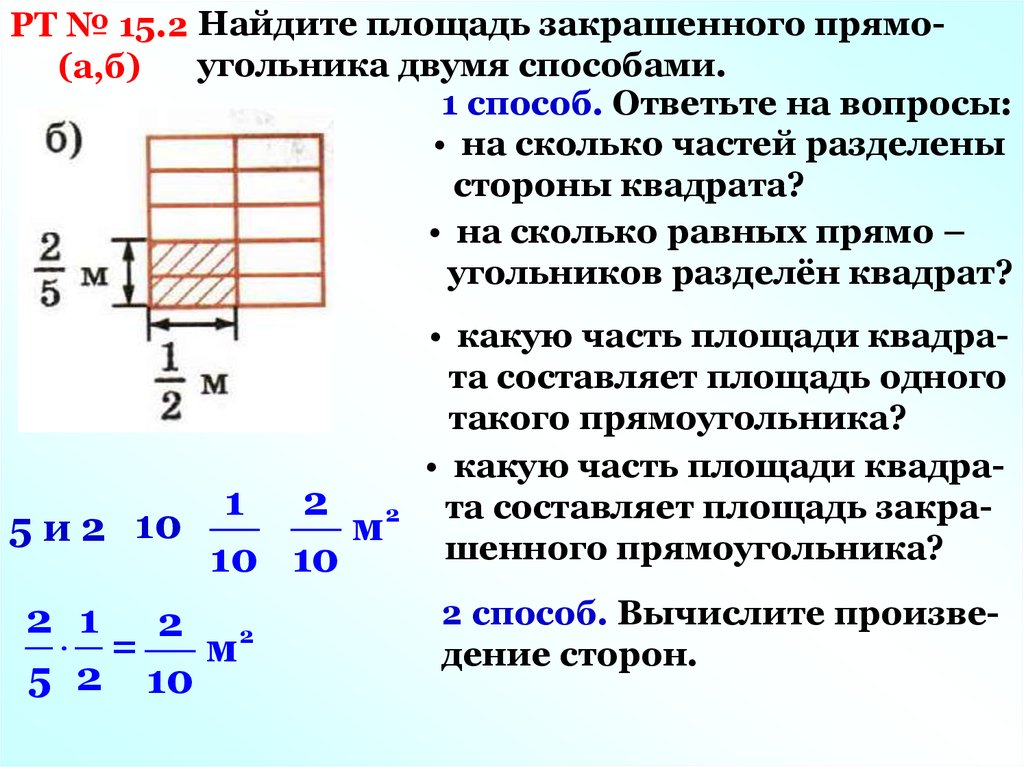
РТ № 15.2 Найдите площадь закрашенного прямоугольника двумя способами.(а,б)
1 способ. Ответьте на вопросы:
• на сколько частей разделены
стороны квадрата?
• на сколько равных прямо –
угольников разделён квадрат?
1 2 2
м
5 и 2 10
10 10
2 1 2 2
=
м
5 2 10
• какую часть площади квадрата составляет площадь одного
такого прямоугольника?
• какую часть площади квадрата составляет площадь закрашенного прямоугольника?
2 способ. Вычислите произведение сторон.
12.
Умножение обыкновенных дробей3 5 3
3 5
3 5 15
=
= 5: 7 =
:7=
4 7 28
4 7 4
4
а c а c
=
b d b d
13.
Произведение обыкновенных дробей –это дробь, числитель которой равен
произведению числителей, а знаменатель
– произведению знаменателей данных
дробей:
а c a c
=
b d b d
14.
Умножениеобыкновенных
дробей
15.
13 5
·
=
4 7
15
28
2
2 8
·
=
3 11
16
33
3 12 · 2
=
24
65
4
5 3
·
=
8 7
15
56
5
8 1
9
·
·
=
9 2
4
1
13
5
16.
РТ № 15.5 Выполните умножение.1
5 4
5
=
8 7 14
2
1 1
1
2 3
=
9 8 12
3
4
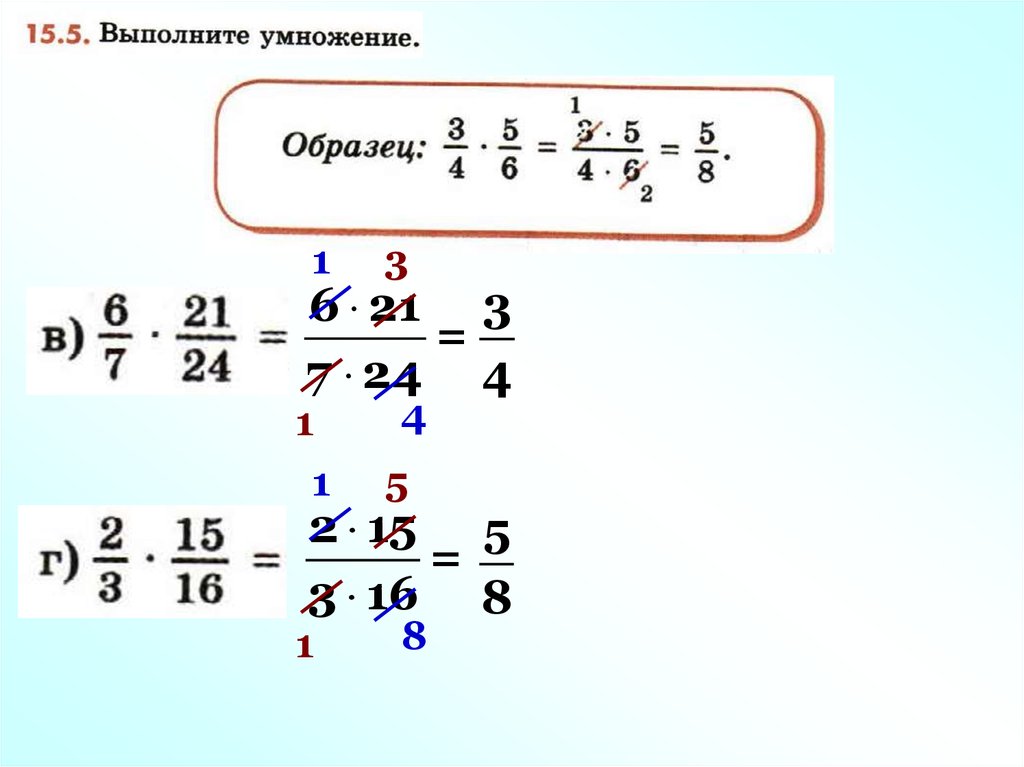
17.
13
6 21 3
=
7 24 4
1
1
4
5
2 15 5
=
3 16 8
1
8
18.
У: № 446 – 449;РТ: № 15.3; 15.7
19.
15.1Умножение и деление
обыкновенных
дробей
20.
1 Вычислите:3·5
3
5
а) 7 · 8 =
=
7·8
15
56
1
4 · 11
4·1
4
11
4
=
б) 33 · 19 =
=
57
33 · 19
3 · 19
3
21.
1 Вычислите:15
в) –
17
15 · 1
15
1
–
=
·
=–
68
4
17 · 4
г) – 3 · – 22
22
3
=
1 1
3 · 22
=
22 · 3
1 1
1·1
=
1·1
1
22.
2 Представьте в виде дроби выражение:m·p
m
p
mp
=
а) n · q =
nq
n·q
4n
p
б) c · 2k
3x
z
в) y · 9t
2
4n · p
2n · p
2np
=
=
=
ck
c · 2k
c·k
1
1
3x · z
x·z
xz
=
=
=
3ty
y · 9t
y · 3t
3
23.
3 Что меньше: разность дробейпроизведение?
4
6
7 и 5 или их
6
9
2
28 – 30 – 1
7
5
1) 9 – 6 =
= 18
36
36
7·5
7
5
2) 9 · 6 =
=
9·6
35
54
Разность дробей меньше, чем их произведение.
Произведение можно было не вычислять.
24.
1 Вычислите:1
4
3
а) 9 · 5 =
4·3
4·1
4
=
=
15
9·5
3·5
3
4
2 · 44
2·4
2
44
8
=
б) 11 · 57 =
=
57
11 · 57
1 · 57
1
25.
1 Вычислите:1
13
в)
· –
8
15
1 · 13
13
–
=
= –
120
8 · 15
г) – 4 · – 31
31
4
=
1 1
4 · 31
=
31 · 4
1 1
1·1
=
1·1
1
26.
2 Представьте в виде дроби выражение:a
n
а) b · k =
6x
z
б) k · 3y
4m s
в) p · 8t
a·n
an
=
bk
b·k
2
6x · z
=
=
k · 3y
1
1
4m · s
=
=
p · 8t
2
2x · z
2xz
=
ky
k·y
m·s
ms
=
2pt
p · 2t
27.
3 Что меньше: разность дробейпроизведение?
4
3
5
2
4–9
1
3
–
1) 6 – 8 =
= 24
36
24
1
1·3 1·1
1
3
2) 6 · 8 =
=
6·8 2·8=
2
1 и 3 или их
8
6
1
16
Разность дробей меньше, чем их произведение
Произведение можно было не вычислять.





















 Математика
Математика








