Моделирование сложных систем

1.

Моделирование сложных систем
ТЕМА 8
ГРИГОРЬЕВ ВА
ВЕРСИЯ 2017
1

2.

СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1) Понятие о модельном времени.
2) Пример имитационного моделирования
сложной системы на базе 3-х компонент.
3) Порядок изменения модельного времени.
ВЕРСИЯ 2017
2

3. Введение

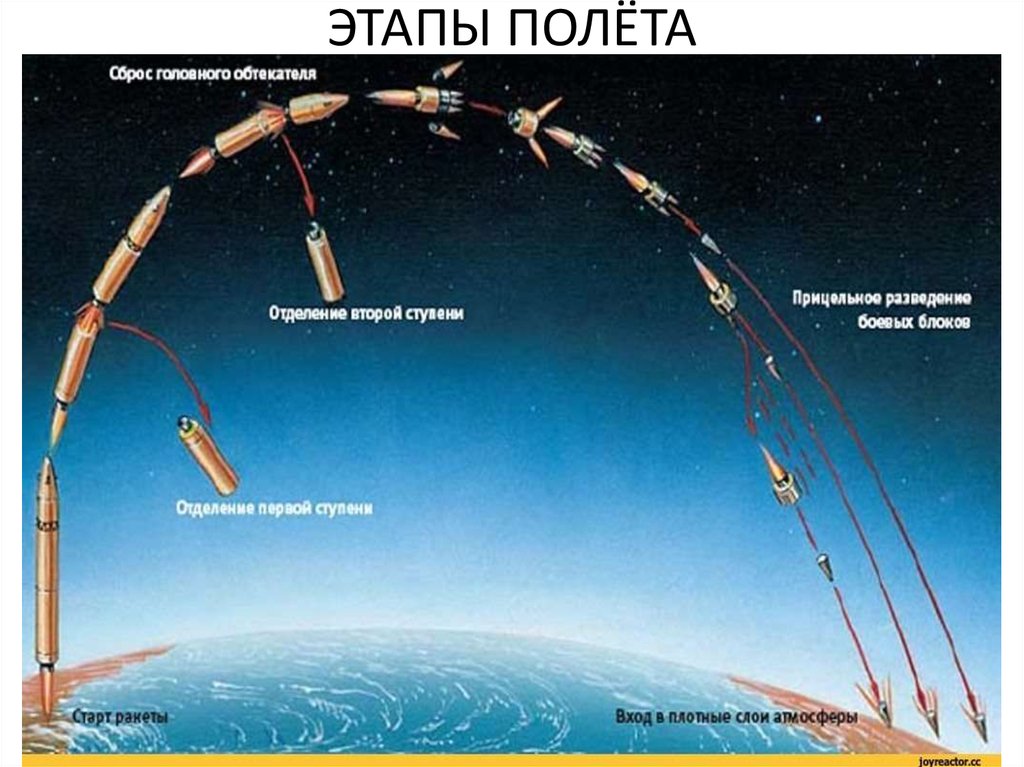
• 19 ноября Россия празднует День ракетных войск и
артиллерии.
• Сегодня
мы
рассмотрим
некоторые
понятия
о
имитационном моделировании Сложных систем на основе
примеров, представленных в учебнике Максимея
«Имитационное моделирование».
• В качестве примера для моделирования рассмотрим
межконтинентальную
баллистическую
ракету
РС-20
«Воевода» (по классификации НАТО «Сатана»).
• Воевода способна поразить цели практически в любой точке
земли. Она оснащается ядерной боеголовкой с 10
разделяющимися зарядами. Точность попадания каждого
заряда +/- 10 метров.
ВЕРСИЯ 2017
3

4. Материалы интернета (открытый доступ)

ВЕРСИЯ 2017
4

5.

ВЕРСИЯ 2017
5

6.

ВЕРСИЯ 2017
6

7.

ВЕРСИЯ 2017
7

8.

ВЕРСИЯ 2017
8

9.

ВЕРСИЯ 2017
9

10.

ВЕРСИЯ 2017
10

11.

ВЕРСИЯ 2017
11

12. ЭТАПЫ ПОЛЁТА

ВЕРСИЯ 2017
12

13.

ВЕРСИЯ 2017
13

14.

ВЕРСИЯ 2017
14

15.

ВЕРСИЯ 2017
15

16. 1. Понятие о модельном времени.

Пример:
Объектом имитации является движение i-той
космической ракеты.
Можно выделить ряд стадий ее движения, в ходе
которых
выполняется
последовательность
функциональных действий (ФД).
Пусть каждая стадия движения ракеты характеризуется
своим номером j.
При j=1 осуществляется запуск ракеты i на стартовой
площадке.
Стадии движения, в ходе которых выполняется
последовательность функциональных действий (ФД):
J=1. На этой стадии выполняется первое
функциональное действие ФДi1.
ВЕРСИЯ 2017
16

17. Первое действие. Осуществляется запуск ракеты i на стартовой площадке. Выполняется функциональное действие ФДi1.

При j=1 осуществляется запуск ракеты
i на стартовой площадке.
выполняется первое
функциональное действие ФДi1.
СОБЫТИЕ Сi1
время
ВЕРСИЯ 2017
17

18. Функциональные действия 2 и 3

• J=2. Коррекция движения и сброс первой
ступени i-й ракеты определяют ФДi2
• J=3. Вторая коррекция движения и сброс
второй ступени i-й ракеты означает
выполнение функционального действия ФДi3
Движение множества ракет представляет
собой сложную систему (СС), и каждая
i-я ракета является компонентой K i.
ВЕРСИЯ 2017
18

19.

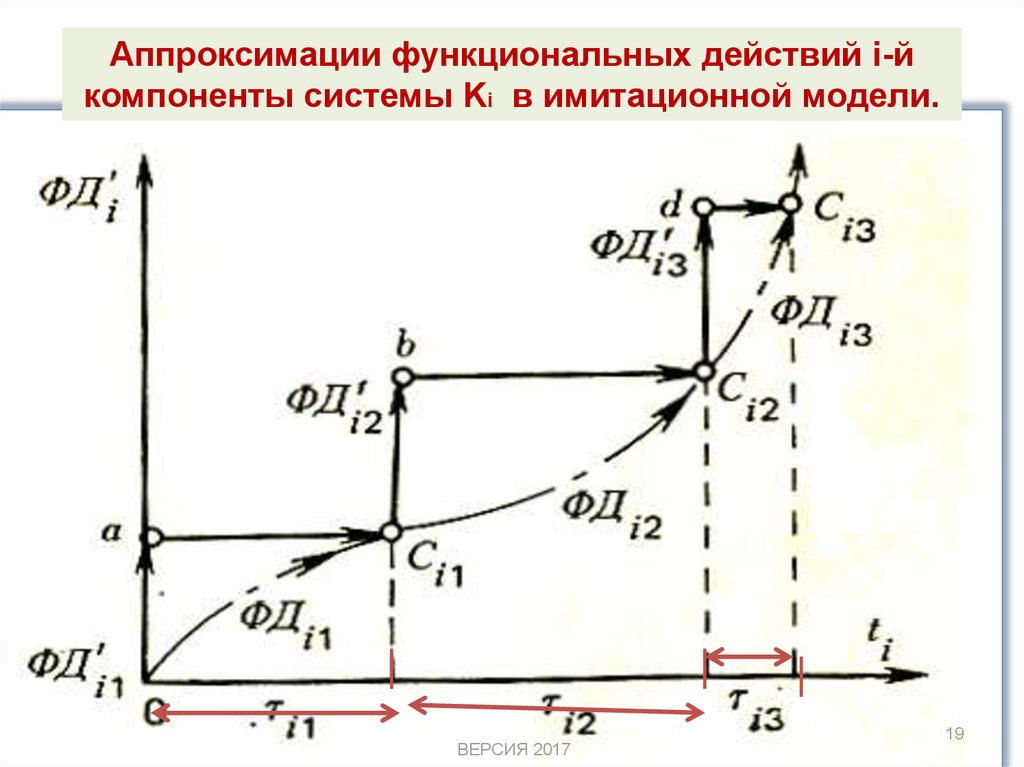
Аппроксимации функциональных действий i-й
компоненты системы Ki в имитационной модели.
ВЕРСИЯ 2017
19

20.

Функционирование компоненты Ki сложной системы
СС представляет собой последовательность
функциональных действий ФД ij.
В результате выполнения ФДij в СС происходят
события Сij.
Каждое из событий в реальной СС связано, как
правило,
с
соответствующей
компонентой
(ракетой) K i.
При этом любое ФДij выполняется на некотором
временном интервале τ ij.
Для каждой Ki введено понятие локального
времени ti.
В СС все ti изменяются одновременно, однако
характер этих изменений различен и определяется
последовательностью временных интервалов {τij}.
ВЕРСИЯ 2017
20

21.

При построении ИМ СС функциональные
действия ФДij аппроксимируются некоторыми
упрощенными функциональными действиями
ФД 'ij реализуемыми при имитации.
• Степень этого упрощения определяет уровень
детализации ИМ. Отличия ФД'ij от ФДij
порождают ошибки имитации реальной СС. В
ИМ ФДij представляется парой (ФД'ij, τij),
которая выполняется следующим образом:
• Вначале реализуется ФД'ij, при неизменном
значении ti, а затем уже отображается
изменение ti на величину τij, инициируя таким
образом появление события Сij.
ВЕРСИЯ 2017
21

22.

В ходе имитации происходят
реализация
ФД'ij
по
соответствующим алгоритмам АЛij
и последующее изменение ti на
величину τij.
Пару (АЛij, τij) обычно называют
ij-й активностью ИМ и обозначают
АКij.
ВЕРСИЯ 2017
22

23. Пример имитационного моделирования СС на базе 3-х компонент.

Пример имитационного моделирования СС на базе 3х компонент.
Если бы на ЭВМ имитировалось поведение
только одной компоненты системы, то
выполнение активностей в ИМ можно была бы
осуществить строго последовательно, и дело
свелось бы к пересчету временной координаты ti
после очередного выполнения алгоритма АЛij. В
действительности СС состоит из нескольких
компонент.
Все эти компоненты Ki функционируют
одновременно. Это должна отражать ИМ. Чтобы
обеспечить имитацию параллельных событий
реальной системы, вводят некоторую глобальную
переменную to, которую называют модельным
(системным) временем.
С
помощью
этой
переменной
организуются
синхронизация всей событий Сij в модели и
выполнение алгоритмов АЛij компонент Кi модели
системы.
ВЕРСИЯ 2017
23

24. При реализации ИМ используются обычно три представления времени:

• tR — реальное время системы, работа
которой имитируется на данной ИМ;
• to — модельное время, по которому
организуется синхронизация событий в
системе;
• t3 — машинное время имитации,
отражающее затраты ресурса времени
ЭВМ на организацию имитации.
ВЕРСИЯ 2017
24

25.

ракета
i=1
ракета
i=2
ракета
i=3
время
Временная диаграмма моделирования событий в реальной
ВЕРСИЯ 2017
сложной системе из 3-х компонент
25

26. 3 Порядок изменения модельного времени.

Существуют два способа изменения
модельного времени t0: c помощью
фиксированных
и
c
помощью
переменных интервалов изменения
модельного времени.
Часто их называют соответственно
• способами фиксированного шага
• и шагов до следующего события.
ВЕРСИЯ 2017
26

27.

Для того чтобы легче было представить
оба
способа
организации
изменения
модельного времени, рассмотрим следующий
пример (Pис 1.).
• Пусть в системе функционируют три
компоненты Ki (i=1,2,3).
• При функционировании компоненты К1
последовательно происходят четыре события
(С11, С12, С 13, С14) соответственно четырем
моментам изменения t1 (t11, t12, t13, t14).
• Между этими моментами K1 выполняет
четыре различных функциональных действия
(ФД11, ФД12, ФД13, ФД14).
ВЕРСИЯ 2017
27

28.

• Каждое из указанных функциональных
действий выполняется в течение
соответствующих интервалов времени
(τ11, τ12, τ13, τ14) .
• Аппроксимация ФДij осуществляется
последовательностью {ФД‘1j}, J=1,…,4.
• Аналогичным образом выполняются
функциональные
действия
для
компонент системы К2, К3.
ВЕРСИЯ 2017
28

29.

Корректировка
временных
координат
ti
нескольких Ki ИМ осуществляется с помощью
модельного времени to следующим образом:
Если значения ti при выполнении АЛij
нескольких Ki совпадают (это означает, что в
реальной системе происходит одновременно
несколько событий Сij), то
последовательно
обслуживаются
AЛij,
совпадающие по времени выполнения, т. е.
имеющие
одинаковые
значения
наступления события.
При этом модельное время t0 не меняется до
окончания выполнения всех совпавших по
времени реализации алгоритмов AЛij.
ВЕРСИЯ 2017
29

30.

Таким
способом
последовательно
выполняются соответствующие ФД‘ij при
неизменном значении t0.
После
каждой
реализации
AЛij,
обеспечивающей выполнение в ИМ
функциональные
действия
ФД‘ij,
выполняется оператор корректировки
временной координаты Mtij.
Чаще всего эта корректировка сводится к
вычислению нового значения tij по
формуле:
tij= t0+ τij
ВЕРСИЯ 2017
30

31. Независимо от способа изменения t0 механизм регламентации изменения модельного времени обычно предусматривает выполнение

следующих
действий:
1) выбор событий в модели, которые необходимо
обслужить при одном и том же модельном
времени t0,
2)
обслуживание
событий
(инициализация
активностей), которые имеют одинаковое время
инициализации;
3) по окончании обслуживания всех одновременных
(в пределах шага) событий определение
очередного значения модельного времени;
4) корректировка временной координаты модели to;
5) проверка условий окончания моделирования
либо по времени завершения имитации, либо по
выполнению других событий в системе.
ВЕРСИЯ 2017
31

32.

ВЕРСИЯ 2017
32

33.

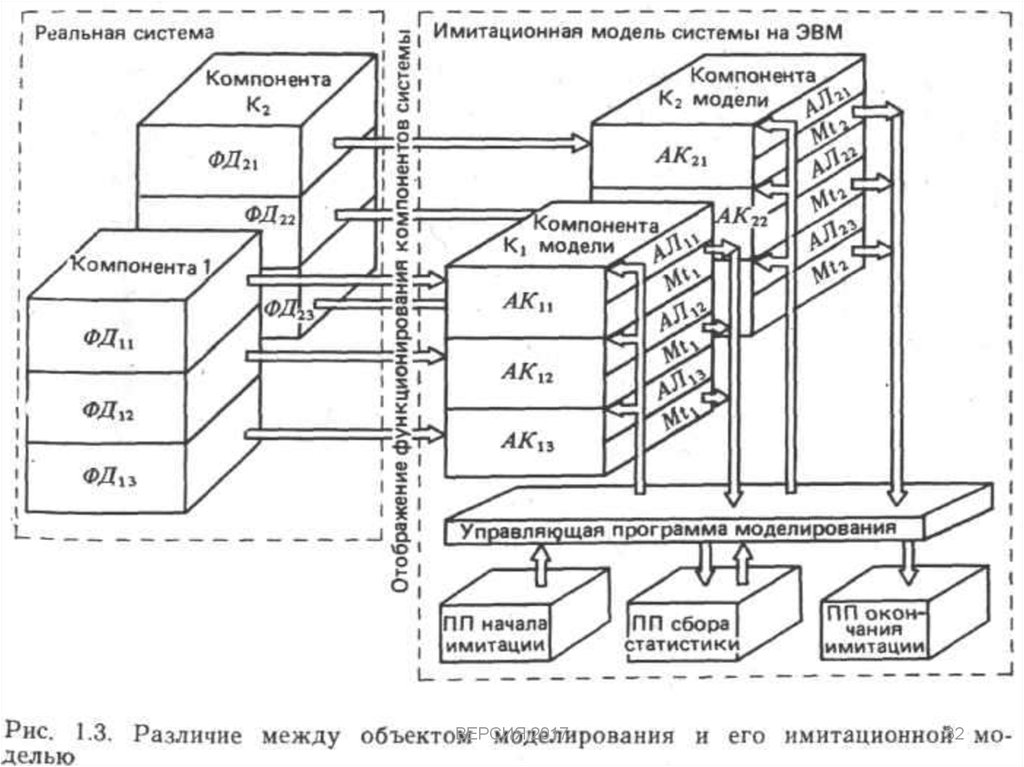
• На рис. 1.3 представлена схема перевода
объекта моделирования в его имитационную
модель. Из рисунка видно, что любое ФДij в ИМ
описывается соответствующей
активностью
АKij.
• Каждая AKij представляет собой попарное
сочетание описания алгоритма АЛij и оператора
модификации
временной
координаты
компоненты модели Mtij.
• Управляющая программа моделирования (УПМ)
передает управление на начало программы,
реализующей алгоритмы АЛij. Возврат на УПМ
имеет место при выполнении операторов Mtij.
ВЕРСИЯ 2017
33

34.

ВЕРСИЯ 2017
34

35. ПОРЯДОК ИЗМЕНЕНИЯ МОДЕЛЬНОГО ВРЕМЕНИ

Существует
два
основных
подхода
к
продвижению модельного времени:
1. продвижение времени от события к событию
2. продвижение времени с постоянным шагом.
• Подход, использующий продвижение времени
в модели от события
к
событию,
применяется
всеми
основными
компьютерными
программами
и
большинством разработчиков программ.
ВЕРСИЯ 2017
35

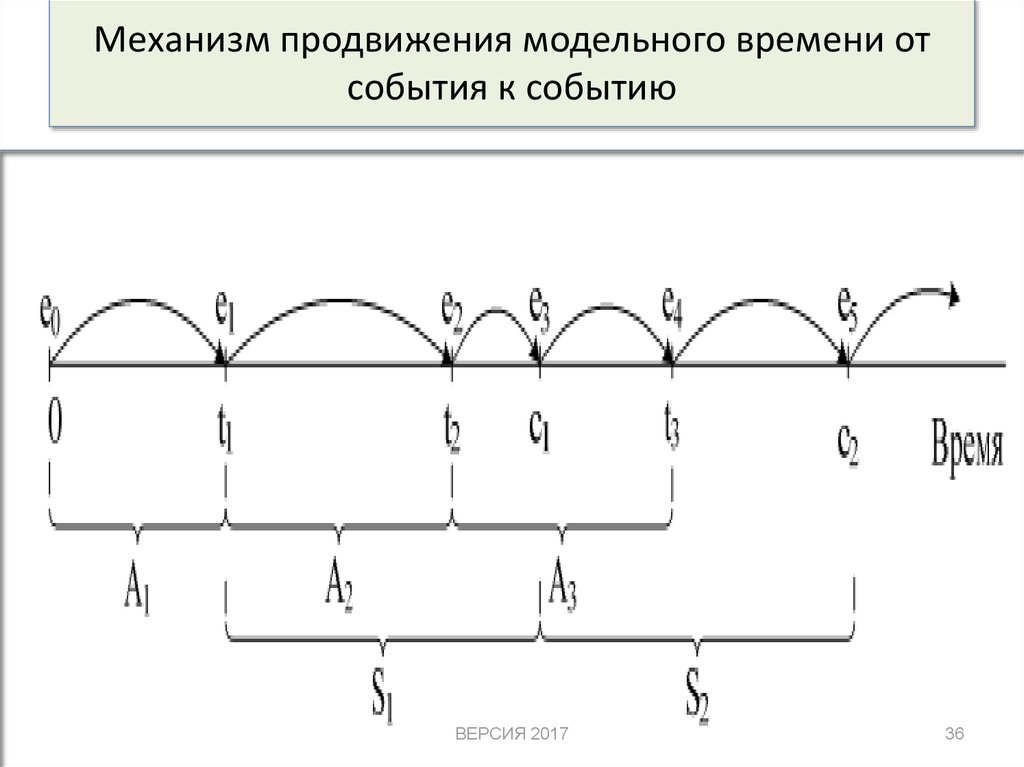
36. Механизм продвижения модельного времени от события к событию

ВЕРСИЯ 2017
36

37.

При использовании продвижения времени от события к
событию
• часы модельного времени в исходном состоянии
устанавливаются
в 0, и определяется время
возникновения будущих событий.
• После этого часы модельного времени переходят на
время возникновения ближайшего события, и в этот
момент обновляются состояние системы, с учетом
произошедшего события, а также сведения о
времени возникновения будущих событий.
• Затем часы модельного времени продвигаются ко
времени возникновения
следующего
нового
ближайшего события, обновляется состояние системы
и определяется время будущих событий и т. д.
ВЕРСИЯ 2017
37

38.

• Процесс продвижения модельного времени от времени
возникновения одного события ко времени возникновения
другого продолжается до тех пор, пока не будет выполнено
какое-либо условие останова, указанное заранее.
• Поскольку в дискретно-событийной имитационной модели все
изменения происходят только во время возникновения событий,
периоды бездействия системы просто пропускаются, и часы
переводятся со времени возникновения одного события на
время возникновения другого.
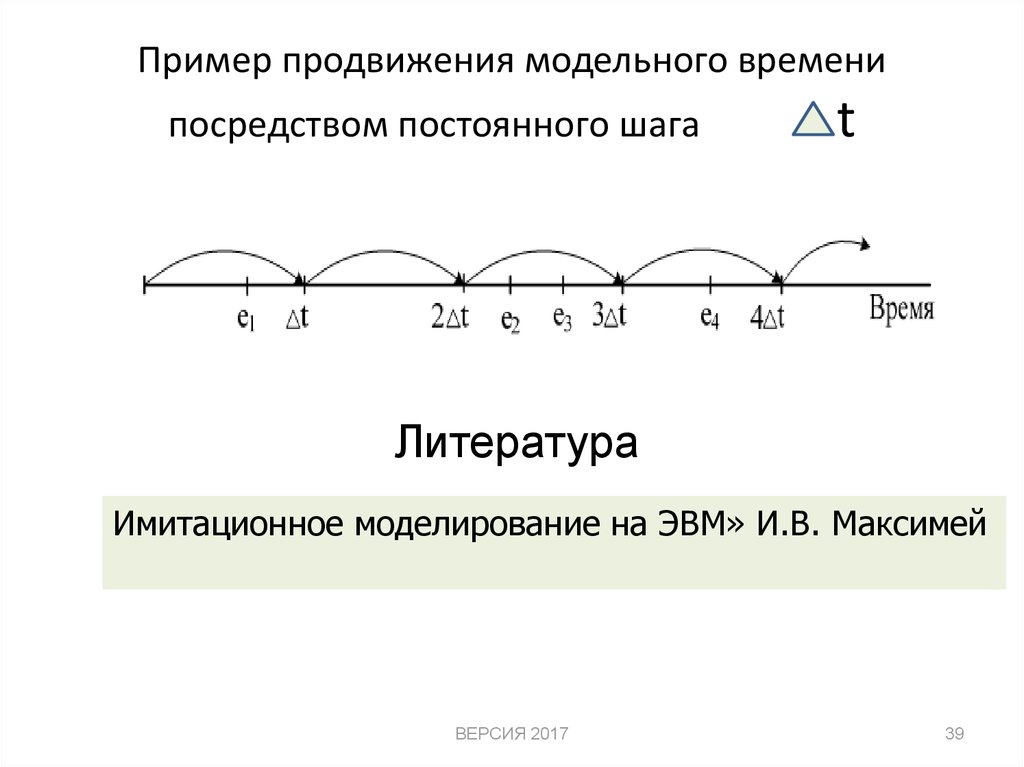
• При продвижении времени с постоянным шагом такие периоды
бездействия не пропускаются, что приводит к большим затратам
компьютерного времени. Следует отметить, что длительность
интервала продвижения модельного времени от одного
события к другому может быть различной .
ВЕРСИЯ 2017
38

39. Пример продвижения модельного времени посредством постоянного шага t

Литература
Имитационное моделирование на ЭВМ» И.В. Максимей
ВЕРСИЯ 2017
39