Похожие презентации:
Podstawy algorytmów ewolucyjnych
1. Podstawy algorytmów ewolucyjnych
Dariusz BaduraWyższa Szkoła Biznesu
Katedra Informatyki
2. Ewolucyjne przeszukiwanie
... oznaczać będzie poszukiwanie rozwiązania problemu –zadania poprzez wprowadzenie losowego generowania
rozwiązań z wykorzystaniem operatorów genetycznych.
Aktywne przeszukiwane nazywać będziemy aktywnym, jeżeli w
poszukiwaniu rozwiązania będzie wykorzystana wiedza o
problemie ułatwiająca podjęcie decyzji o kierunku poszukiwań
rozwiązania.
W celu porównania skuteczności ewolucyjnego i losowego
przeszukiwania należałoby porównać czas poszukiwania
satysfakcjonującego rozwiązania obiema metodami.
3. Metody ewolucyjne
... algorytmy ewolucyjne obejmują następującemetody rozwiązywania problemów:
• algorytmy ewolucyjne „ciągłe”,
• algorytmy genetyczne,
• programowanie genetyczne,
• projektowanie ewolucyjne DNA
4. Pokrewne metody metod ewolucyjnych
... , w których wprost lub pośrednio występujeewoluująca bądź operacje na populacjach np.:
• metoda sztucznej immunologii
• PSO – (ang. particle swarm optimization) –
optymalizacja roju cząstek
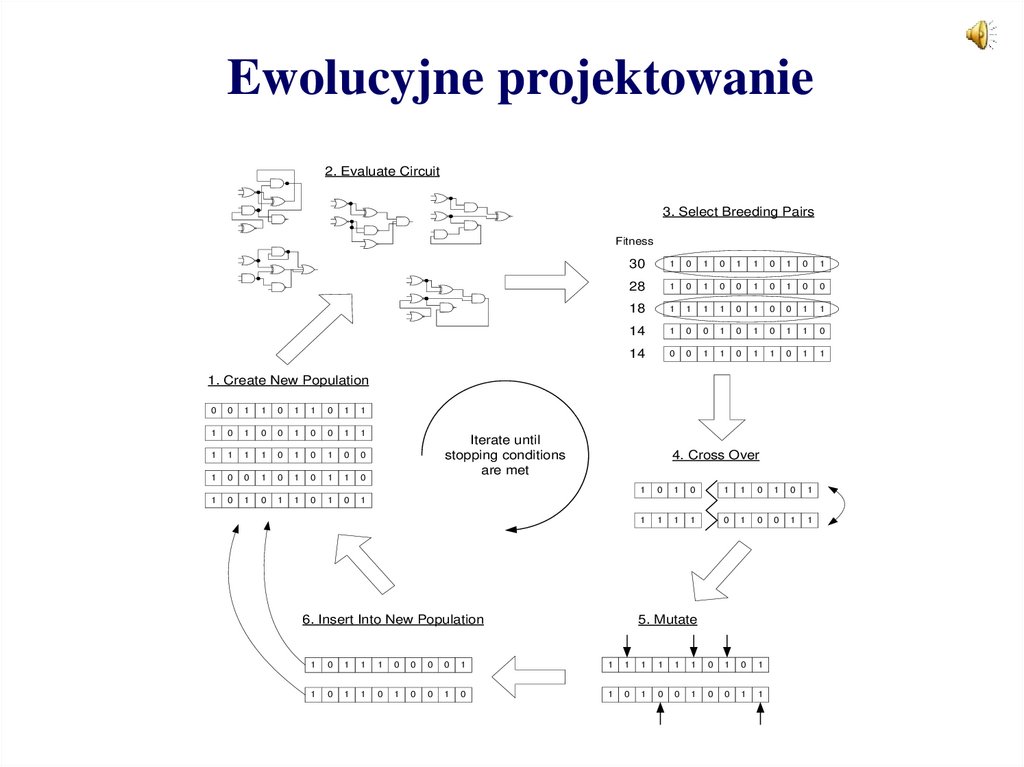
5. Ewolucyjne projektowanie
2. Evaluate Circuit3. Select Breeding Pairs
Fitness
30
1
0
1
0
1
1
0
1
0
1
28
1
0
1
0
0
1
0
1
0
0
18
1
1
1
1
0
1
0
0
1
1
14
1
0
0
1
0
1
0
1
1
0
14
0
0
1
1
0
1
1
0
1
1
1. Create New Population
0
0
1
1
0
1
1
0
1
1
1
0
1
0
0
1
0
0
1
1
1
1
1
1
0
1
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
1
0
1
1
0
1
0
1
Iterate until
stopping conditions
are met
4. Cross Over
6. Insert Into New Population
1
0
1
0
1
1
0
1
0
1
1
1
1
1
0
1
0
0
1
1
5. Mutate
1
0
1
1
1
0
0
0
0
1
1
1
1
1
1
1
0
1
0
1
1
0
1
1
0
1
0
0
1
0
1
0
1
0
0
1
0
0
1
1
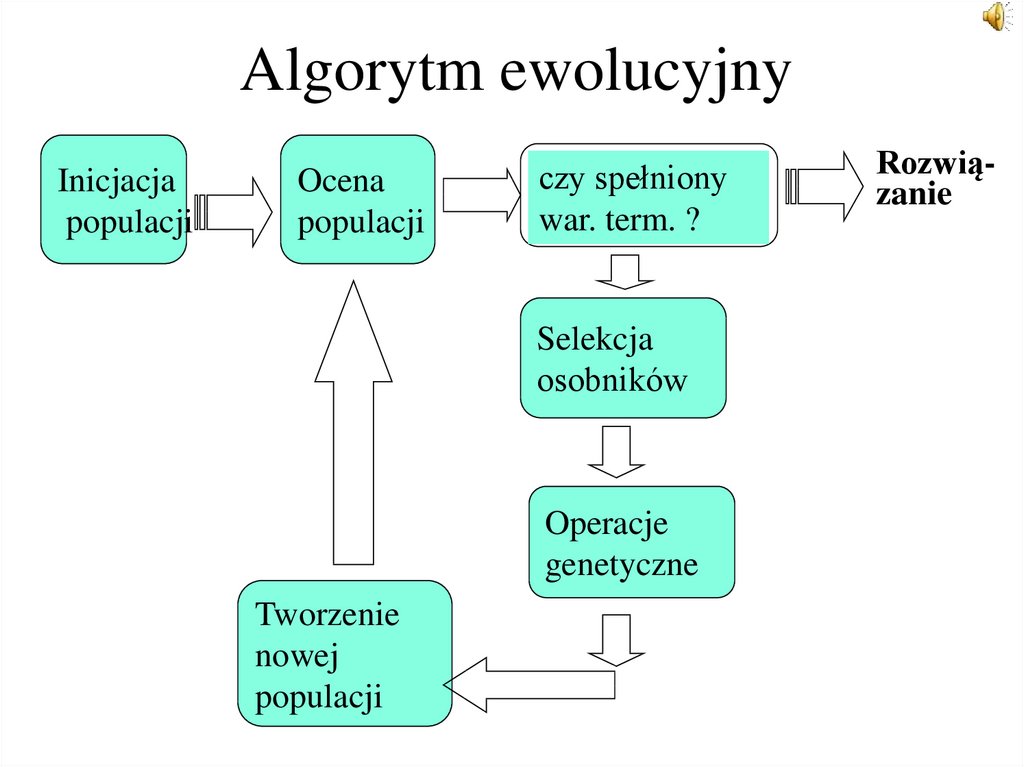
6. Algorytm ewolucyjny
Inicjacjapopulacji
Ocena
populacji
czy spełniony
war. term. ?
Selekcja
osobników
Operacje
genetyczne
Tworzenie
nowej
populacji
Rozwiązanie
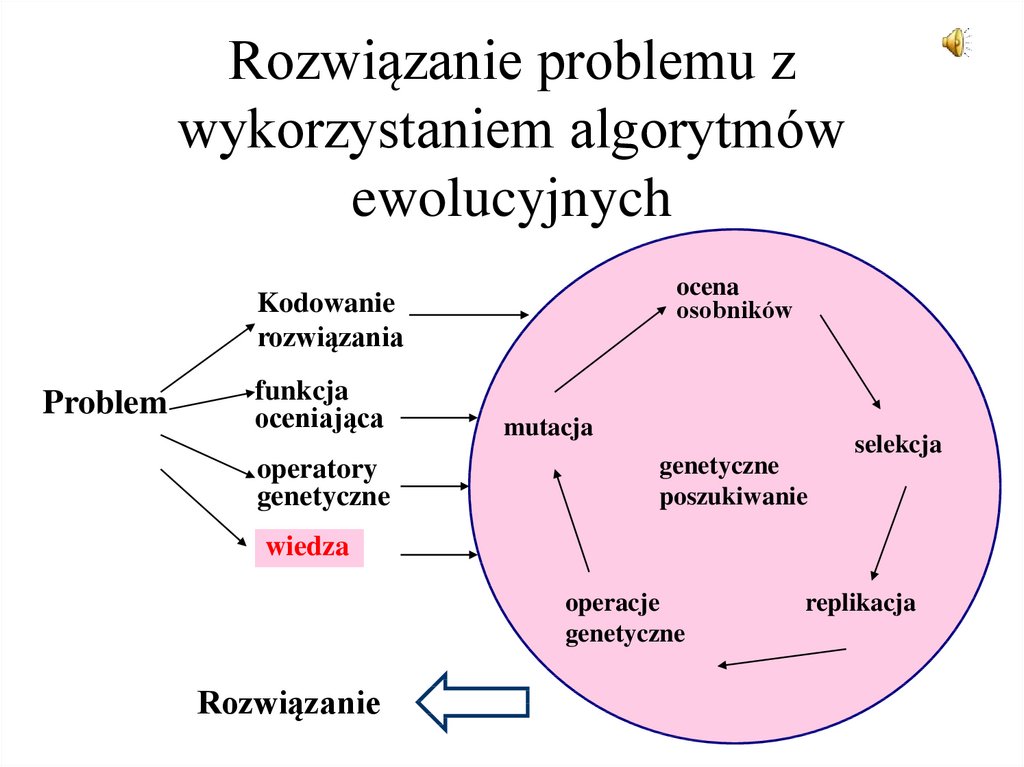
7. Rozwiązanie problemu z wykorzystaniem algorytmów ewolucyjnych
ocenaosobników
Kodowanie
rozwiązania
Problem
funkcja
oceniająca
operatory
genetyczne
mutacja
genetyczne
poszukiwanie
selekcja
wiedza
operacje
genetyczne
Rozwiązanie
replikacja
8. Kodowanie rozwiązania
• EA – algorytmy ewolucyjne• GA – algorytmy genetyczne
• GP – programowanie genetyczne
• DNA – algorytmy oparte o mechanizmy
biologiczno-chemiczne DNA-RNA
9. Kodowanie rozwiązania
• Genotyp – zakodowany opis rozwiązania,na którym wykonywane są operację
genetyczne; często ma postać łańcucha cech
rozwiązania
• Fenotyp –zdekodowany obraz rozwiązania,
który przede wszystkim podczas realizacji
algorytmu służy do wyznaczania funkcji
oceny/ wartości dopasowania
10. Przykład kodowania – problem komiwojażera
• Rozwiązaniem problemu jest łańcuch prezentującykolejność węzłów (miast) w grafie (odwiedzanych przez
komiwojażera).
• Najprostsze kodowanie odpowiada ciągowi numerów
węzłów w grafie. Takie kodowanie jest jednak źródłem
problemów podczas realizacji algorytmów i wymaga
stosowania procedur „naprawczych”
• Innym sposobem kodowania tego problemu jest na
przykład wskazanie numeru aktualnej pozycji węzła w
ciągu liczonej od aktualnej pozycji łańcucha, przy czym
wskazywanie tego miejsca jest procesem
11. Kodowanie ciągu węzłów
numer pozycji, zktórą dokonano
zamiany
Kodowanie ciągu węzłów
kod :
1
3
4( 6)
2( 5)
4( 4)
1( 3)
2
1( 2)
1
2
5
1
2
3
2
3
4
6
4
4
5
1
5
6
4
6
1 6
1 5
1 4
1 3
1 2
wartościowość
• Procedura opisuje sposób uzyskania konstrukcji na podstawie
kodu genów – odwrotnie do metody uzyskania kodu.
• Kodowanie zapewnia poprawność operacji genetycznych.
• Wadą jest zmienna wartościowość pozycji
12. Operatory genetyczne
• Selekcja• Krzyżowanie
• Mutacja
13. Podstawy operacji selekcji
• Funkcja oceny / funkcja dostosowania• proporcjonalne przypisanie wartości
dostosowania
• przypisanie wartości dostosowania na podstawie
rankingu
14. Selekcja – zasady ogólne
Podczas selekcji wyznaczane są osobniki biorąceudział w doborze osobników przed tworzeniem
osobników potomnych.
Krok pierwszy – przypisanie wartości
przystosowania.
Krok drugi – przypisanie prawdopodobieństwa
reprodukcji zależne od jego wartości dostosowania oraz
od wartości pozostałych osobników puli selekcyjnej.
15. Selekcja
Osobniki rodzicielskie są wybierane na podstawiewartości funkcji dostosowania za pomocą
następujących algorytmów:
• selekcja koła ruletki,
• stochastycznego uniwersalnego próbkowania,
• selekcja lokalna,
• selekcji odcięcia lub
• selekcji turniejowej.
16. Selekcja – parametry
Presja selekcji – selective pressure:Prawdopodobieństwo najlepszego osobnika będącego w selekcji
porównane do średniego prawdopodobieństwa selekcji
wszystkich osobników.
Skłonność – bias:
Wartość absolutna różnicy pomiędzy znormalizowaną wartością
przystosowania osobnika i jego oczekiwanego
prawdopodobieństwa reprodukcji.
Rozpostarcie – spread:
Zakres możliwych wartości liczby potomstwa pochodzących od
osobników.
17. Selekcja – parametry
Utrata różnorodności – loss of diversity:Proporcja osobników populacji, które nie zostały
wyselekcjonowane w fazie selekcji.
Intensywność selekcji – selection intensity:
Oczekiwana średnia wartość dostosowania populacji po
zastosowaniu metody selekcji do znormalizowanego rozkładu
Gaussa.
Wariancja selekcji – selection variance:
Oczekiwana wariancja rozkładu dostosowania populacji po
zastosowaniu metody selekcji do znormalizowanego rozkładu
Gaussa.
18. Metoda rankingu liniowego
Nind – liczba osobników w populacji,Pos – pozycja osobnika w rozpatrywanej populacji. (najmniej
dostosowany osobnik ma wartość Pos=1, a najlepiej
dostosowany osobnik wartość Pos=Nind)
SP – presja selekcji.
Ranking liniowy:
Wartość funkcji dostosowania dla dowolnego osobnika jest
wyznaczana wzorem:
2 * ( SP 1) * ( Pos 1)
Fitness( Pos) 2 SP
Nind 1
Wartość SP (presji selekcji) mieści się w zakresie [1.0, 2.0].
19. Ranking nieliniowy
Dopuszcza większe wartości presji selekcji, przy funkcjidostosowania określonej wzorem:
X ( Pos 1)
Fitness( Pos ) Nind * Nind
X i 1
i 1
X jest pierwiastkiem wielomianu:
0 ( SP Nind ) * X Nind 1 SP * X Nind 2 SP * X SP
lub w innej postaci:
X Nind 1
0 SP *
Nind * X Nind 1
X 1
Ranking nieliniowy pozwala kształtować wartości presji selekcji
(SP) w zakresie [1.0, Nind - 2.0].
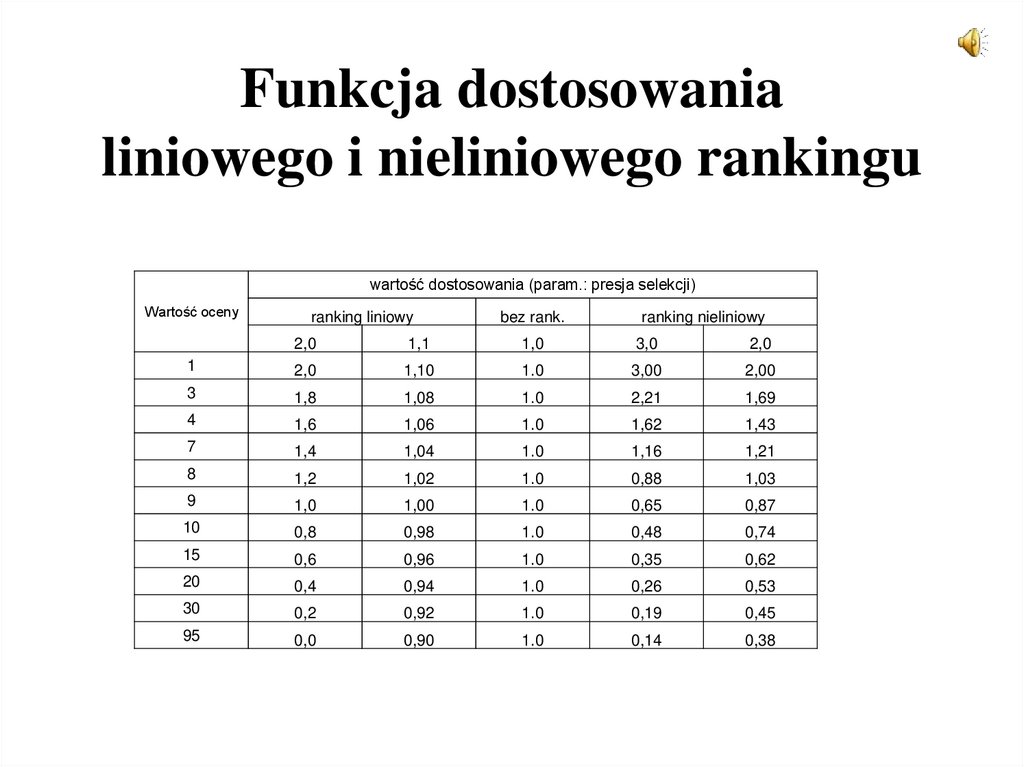
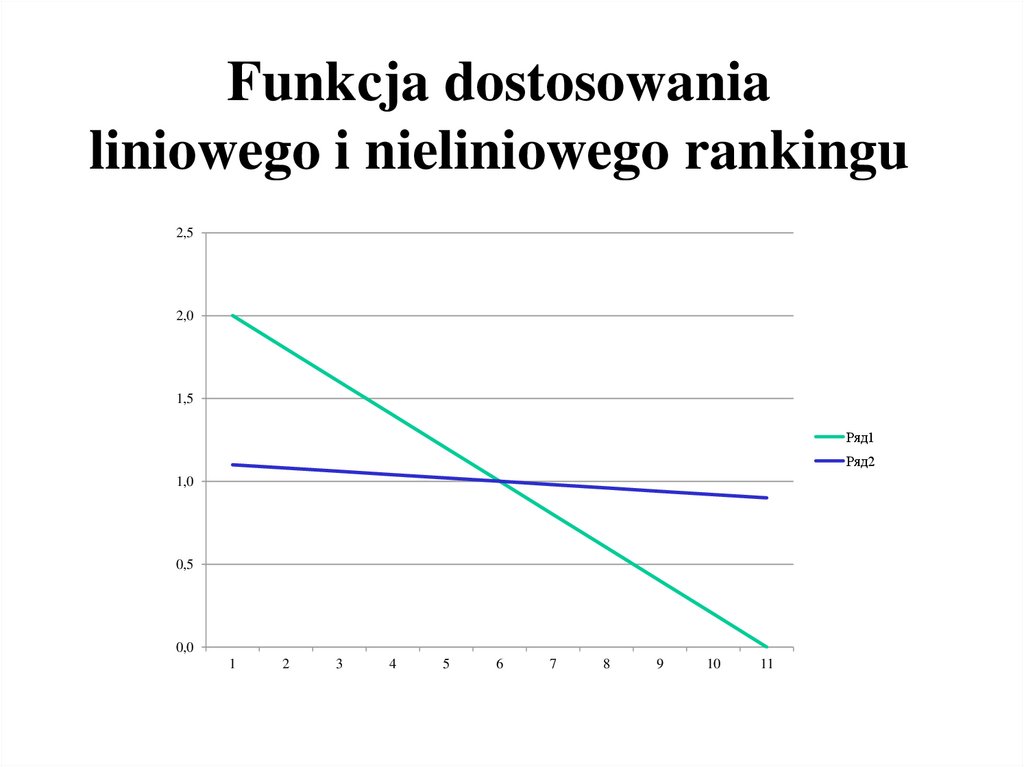
20. Funkcja dostosowania liniowego i nieliniowego rankingu
wartość dostosowania (param.: presja selekcji)Wartość oceny
ranking liniowy
bez rank.
ranking nieliniowy
2,0
1,1
1,0
3,0
2,0
1
2,0
1,10
1.0
3,00
2,00
3
1,8
1,08
1.0
2,21
1,69
4
1,6
1,06
1.0
1,62
1,43
7
1,4
1,04
1.0
1,16
1,21
8
1,2
1,02
1.0
0,88
1,03
9
1,0
1,00
1.0
0,65
0,87
10
0,8
0,98
1.0
0,48
0,74
15
0,6
0,96
1.0
0,35
0,62
20
0,4
0,94
1.0
0,26
0,53
30
0,2
0,92
1.0
0,19
0,45
95
0,0
0,90
1.0
0,14
0,38
21. Funkcja dostosowania liniowego i nieliniowego rankingu
2,52,0
1,5
Ряд1
Ряд2
1,0
0,5
0,0
1
2
3
4
5
6
7
8
9
10
11
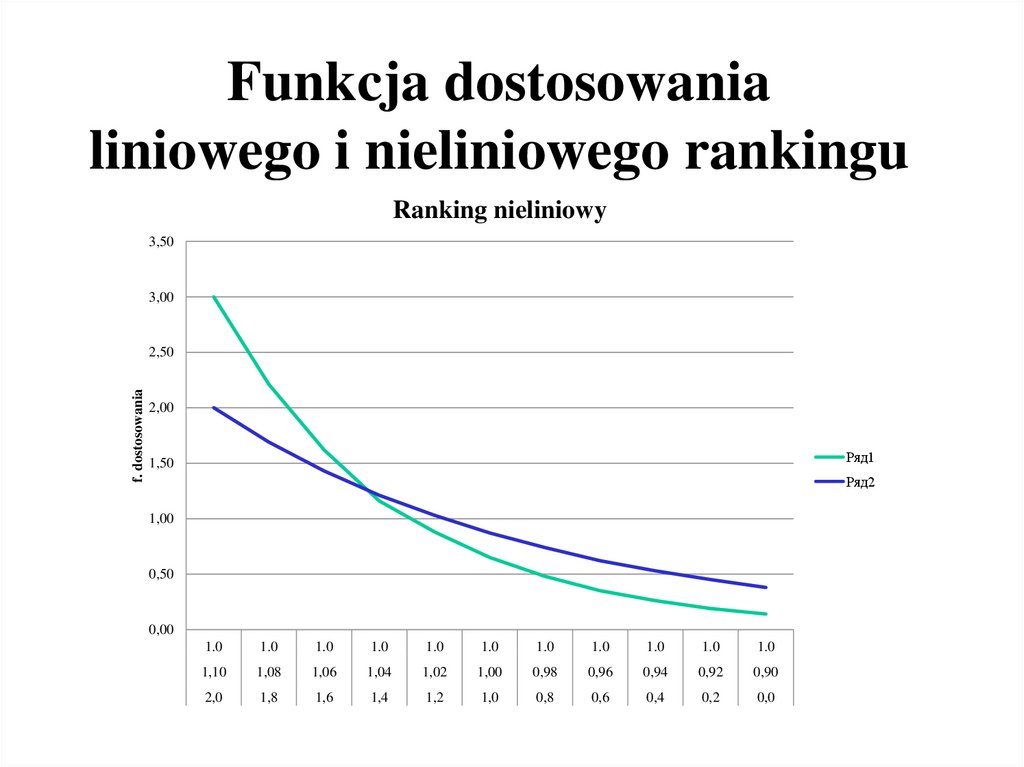
22. Funkcja dostosowania liniowego i nieliniowego rankingu
Ranking nieliniowy3,50
3,00
f. dostosowania
2,50
2,00
Ряд1
1,50
Ряд2
1,00
0,50
0,00
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
1,10
1,08
1,06
1,04
1,02
1,00
0,98
0,96
0,94
0,92
0,90
2,0
1,8
1,6
1,4
1,2
1,0
0,8
0,6
0,4
0,2
0,0
23. Właściwości selekcji rankingowej liniowej
Intensywność selekcji:Utrata różnorodności:
SelInt Rank ( SP ) ( SP 1) *
1
SP 1
LossDiv Rank ( SP )
4
Wariancja selekcji:
SelVarRank ( SP ) 1
( SP 1)2
1 ( SelInt Rank ( SP ))2
24. Właściwości selekcji rankingowej
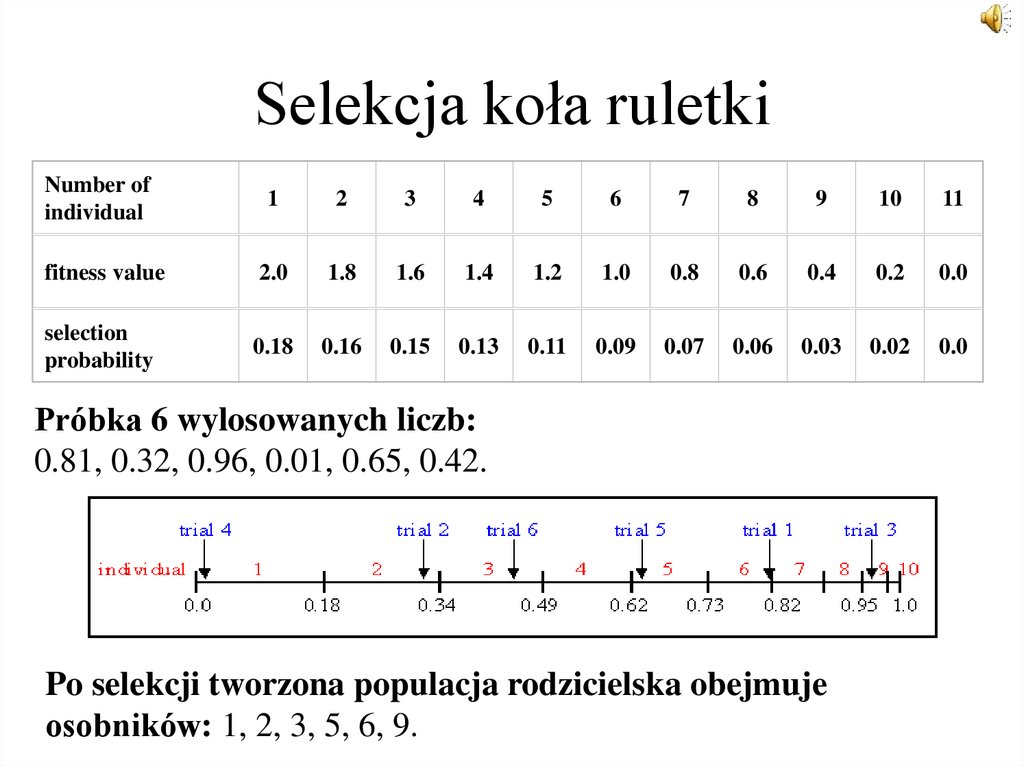
25. Selekcja koła ruletki
Number ofindividual
1
2
3
4
5
6
7
8
9
10
11
fitness value
2.0
1.8
1.6
1.4
1.2
1.0
0.8
0.6
0.4
0.2
0.0
selection
probability
0.18
0.16
0.15
0.13
0.11
0.09
0.07
0.06
0.03
0.02
0.0
Próbka 6 wylosowanych liczb:
0.81, 0.32, 0.96, 0.01, 0.65, 0.42.
Po selekcji tworzona populacja rodzicielska obejmuje
osobników: 1, 2, 3, 5, 6, 9.
26. Stochastyczne uniwersalne próbkowanie
Dla wyselekcjonowania 6 osobników odległość pomiędzywskaźnikami wynosi 1/6=0.167.
Zatem próbka jednej liczby w zakresie [0, 0.167]:
0.1.
Po selekcji populacja rodzicielska zawiera następujące
osobniki:
1, 2, 3, 4, 6, 8.
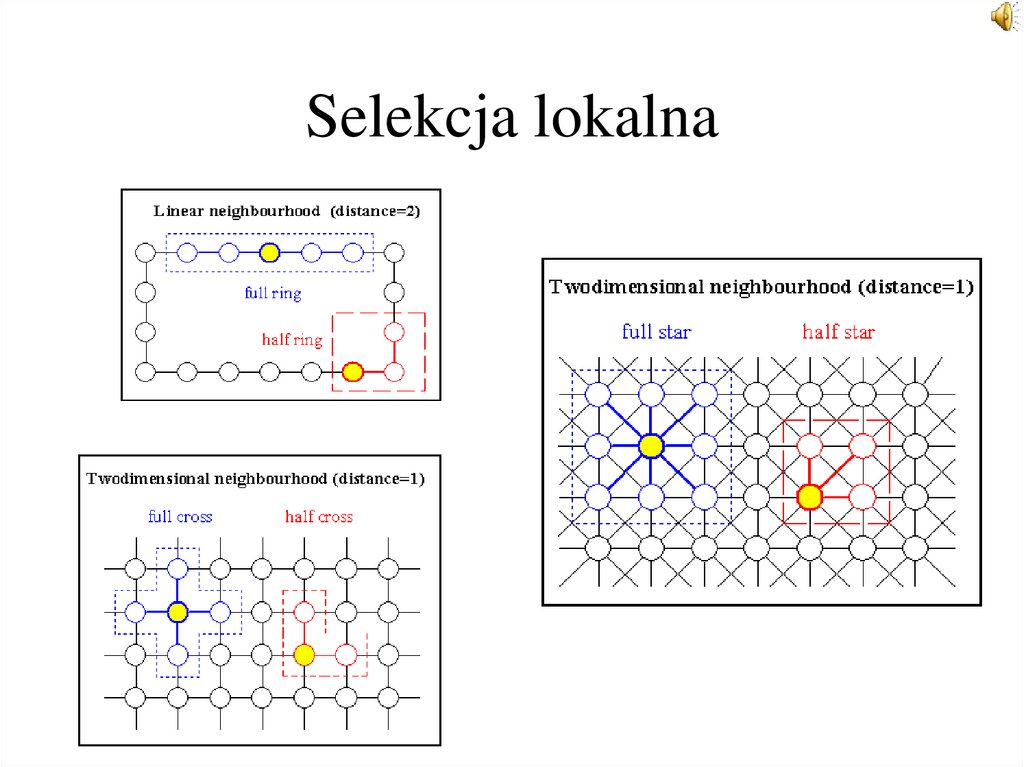
27. Selekcja lokalna
28. Selekcja odcięcia
Zależność pomiędzypoziomem odcięcia a
intensywnością
selekcji
truncation
threshold
1%
10%
20%
40%
50%
80%
Selection
intensity
2.66
1.76
1.2
0.97
0.8
0.34
2
fc
1
SelIntTrunc(Trunc)
*e 2
Trunc * 2 *
Utrata różnorodności:
LossDivTrunc(Trunc) = 1-Trunc.
Wariancja selekcji:
SelVarTrunc(Trunc) = 1-SelIntTrunc(Trunc)·(SelIntTrunc(Trunc)-fc).
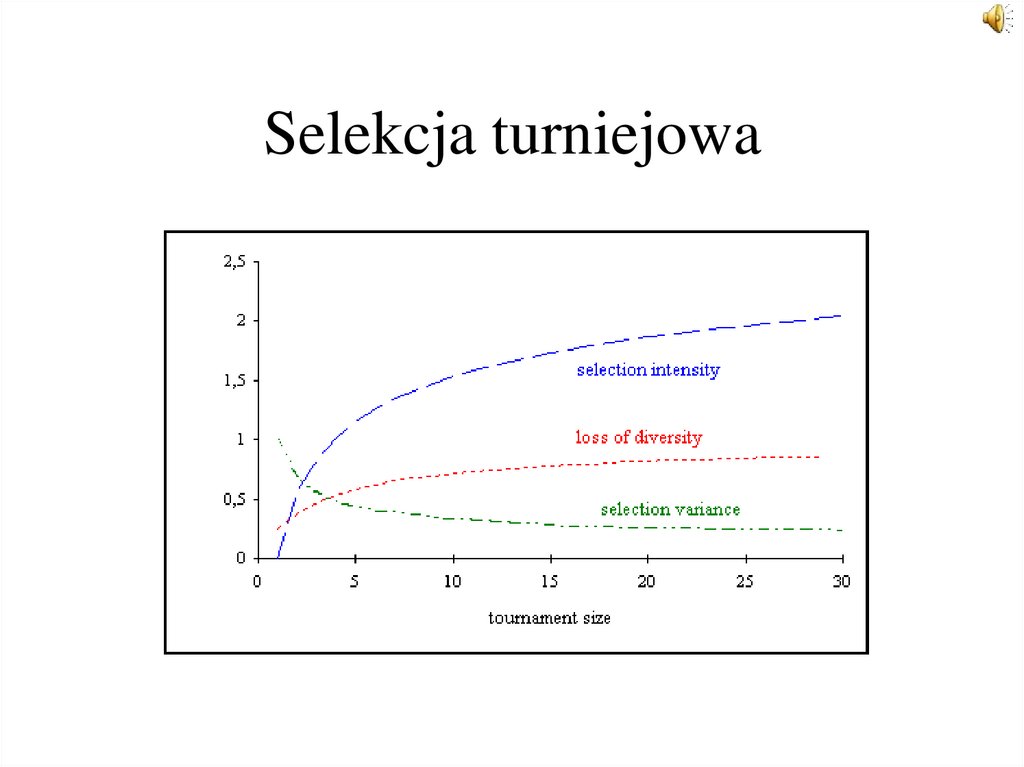
29. Selekcja turniejowa
W selekcji turniejowej pewna liczba Tour osobników zostajelosowo wybrana z populacji.
Następnie wybierana jest podgrupa najlepszych osobników
populacji rodzicielskiej podobnie do turnieju. Proces może być
powtarzany do momentu wypełnienia populacji rodzicielskiej.
Parametry: wielkość turnieju Tour. Tour przyjmuje wartość z
zakresu 2 - Nind.
Tournament size
1
2
3
5
10
30
selection intensity
0
0.56
0.85
1.15
1.53
2.04
30. Selekcja turniejowa
31. Rekombinacja
• Rekombinacja wartości rzeczywistych:o rekombinacja dyskretna,
o rekombinacja pośrednia,
o rekombinacja liniowa,
o poszerzona rekombinacja liniowa.
• Rekombinacja binarna/dyskretna (krzyżowanie):
o
o
o
o
o
krzyżowanie jednopunktowe,
krzyżowanie wielopunktowe,
krzyżowanie unormowane,
krzyżowanie typu tasowanie,
krzyżowanie ze zredukowanym surogatem.
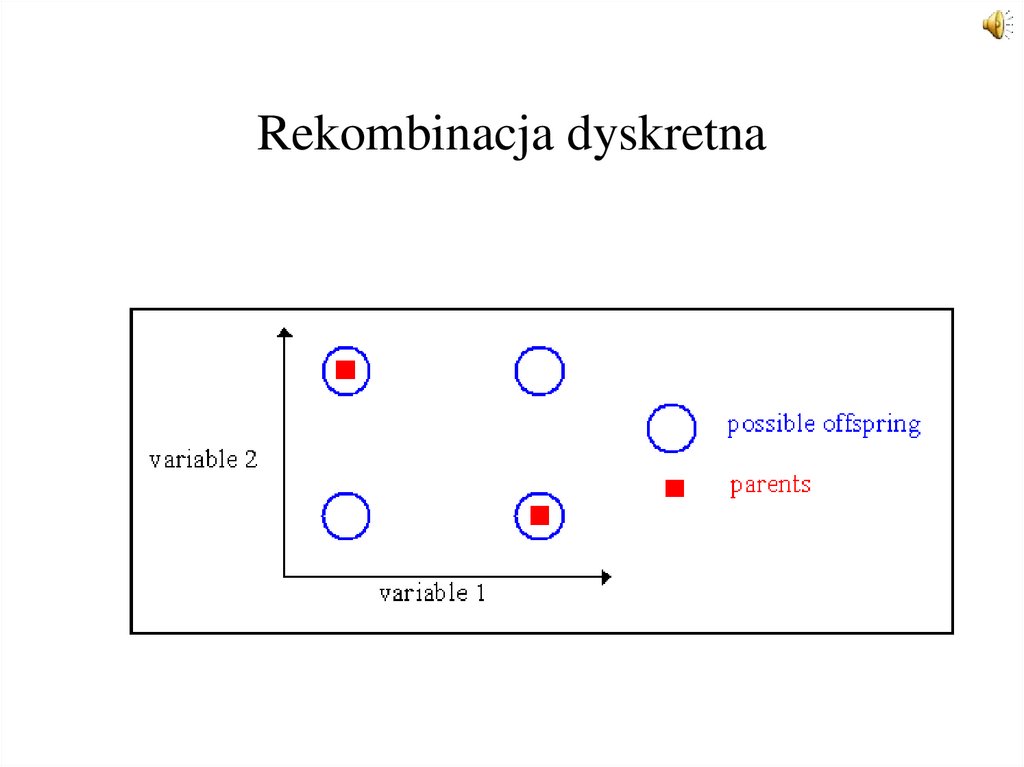
32. Rekombinacja wartości rzeczywistych – rekombinacja dyskretna
Rekombinacja dyskretna dokonuje wymiany wartości zmiennychpomiędzy osobnikami.
Przykład: dwa osobniki z trzema zmiennymi (3 wymiary):
osobnik 1
12
25
5
osobnik 2
123
4
34
Dla każdej zmiennej wybór wartości jednego z rodziców jest
dokonywana w sposób losowy z równym prawdopodobieństwem
dla każdego z rodziców.
próbka 1
2
2
1
próbka 2
1
2
1
Po rekombinacji tworzone są nowe osobniki:
potomek 1
123
4
5
potomek 2
12
4
5
33. Rekombinacja dyskretna
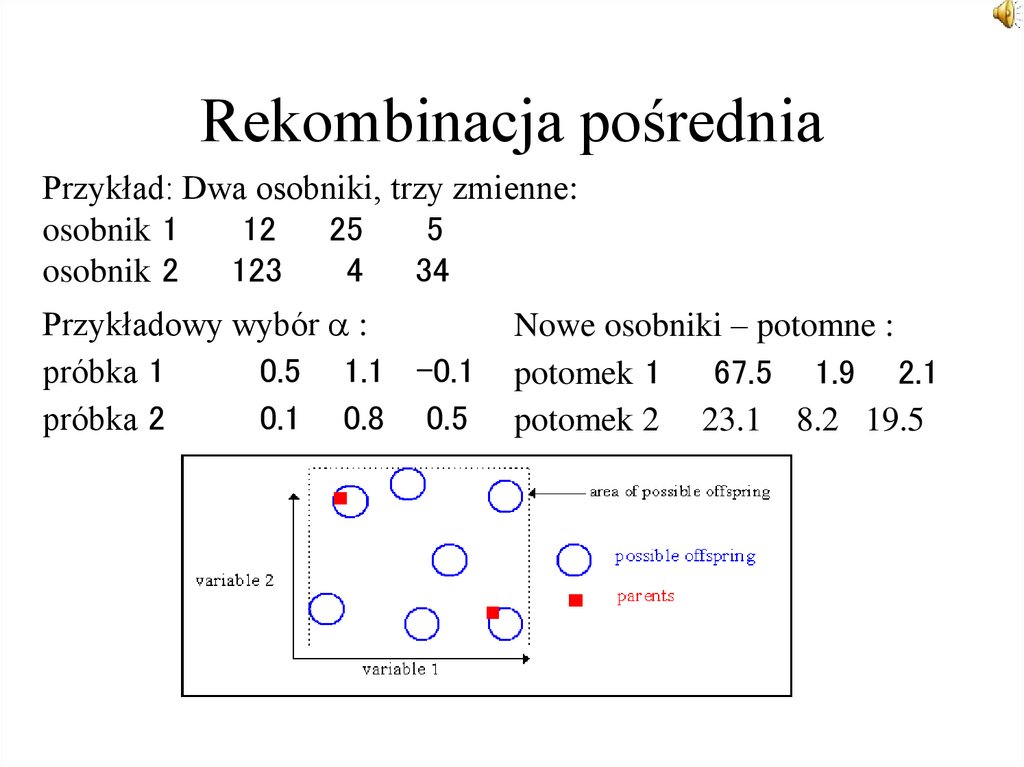
34. Rekombinacja pośrednia
Potomne osobniki są zgodnie z następującą regułą:potomek = rodzic 1 + (rodzic 2 – rodzic 1),
gdzie jest współczynnikiem skalującym wybieranym w sposób
losowy z równym prawdopodobieństwem z zakresu [-d, 1 + d].
Dla rekombinacji pośredniej d = 0, dla rozszerzonej rekombinacji
pośredniej d > 0. Dobrą wartością jest d = 0.25. Dla każdej
zmiennej współczynnik jest losowany oddzielnie.
35. Rekombinacja pośrednia
Przykład: Dwa osobniki, trzy zmienne:osobnik 1
12
25
5
osobnik 2
123
4
34
Przykładowy wybór :
próbka 1
0.5 1.1 -0.1
próbka 2
0.1 0.8 0.5
Nowe osobniki – potomne :
potomek 1
67.5 1.9 2.1
potomek 2 23.1 8.2 19.5
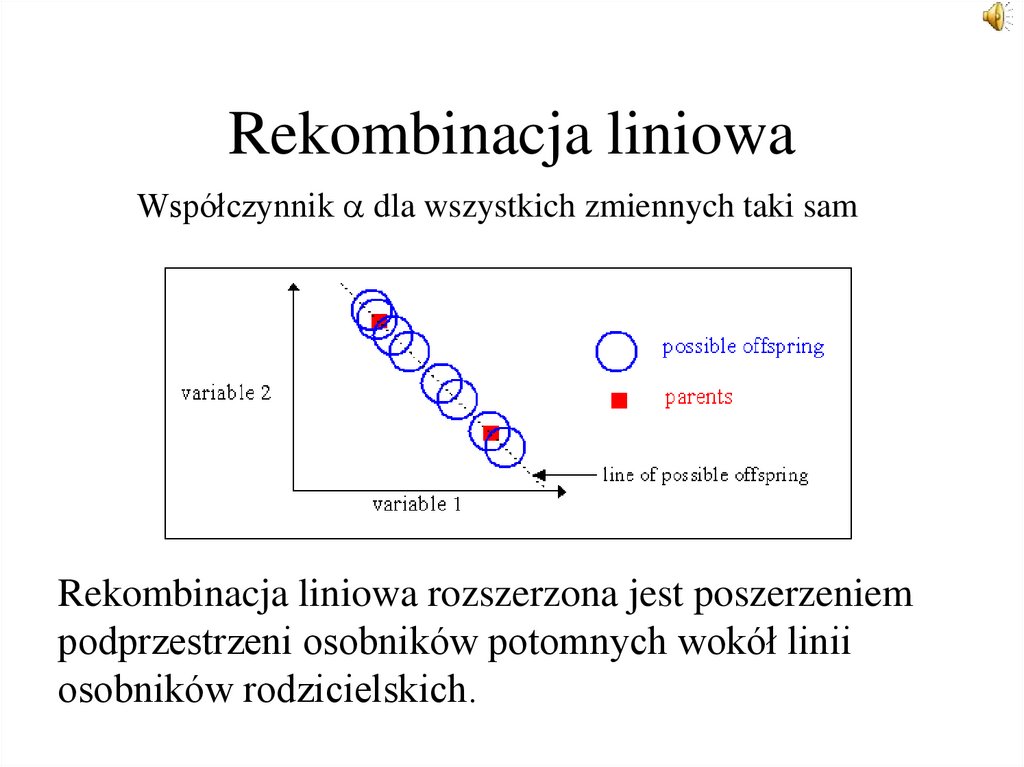
36. Rekombinacja liniowa
Współczynnik dla wszystkich zmiennych taki samRekombinacja liniowa rozszerzona jest poszerzeniem
podprzestrzeni osobników potomnych wokół linii
osobników rodzicielskich.
37. Krzyżowanie jednopunktowe
Dwa osobniki z 11 wartościami binarnymi:individual 1
0 1 1 1 0 0 1 1 0 1 0
individual 2
1 0 1 0 1 1 0 0 1 0 1
Wybrany zostaje punkt krzyżowania:
punkt krzyżowania
5
Po krzyżowaniu otrzymamy następujące osobniki potomne:
offspring 1
0 1 1 1 0| 1 0 0 1 0 1
offspring 2
1 0 1 0 1| 0 1 1 0 1 0
38. Krzyżowanie wielopunktowe
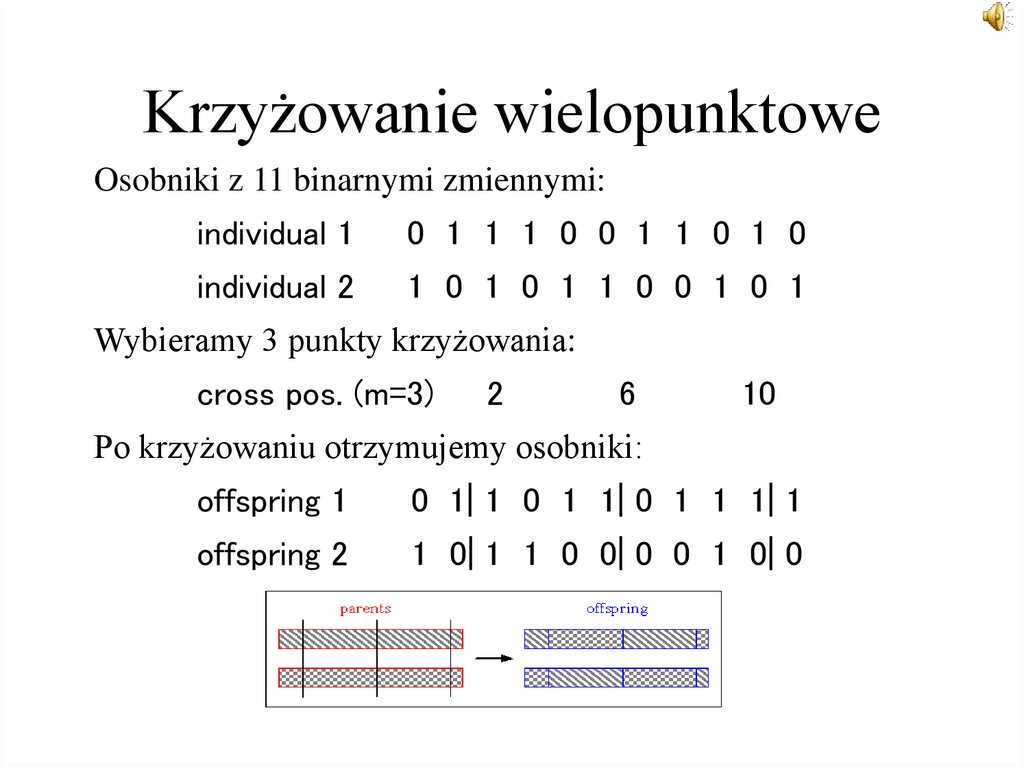
Osobniki z 11 binarnymi zmiennymi:individual 1
0 1 1 1 0 0 1 1 0 1 0
individual 2
1 0 1 0 1 1 0 0 1 0 1
Wybieramy 3 punkty krzyżowania:
cross pos. (m=3)
2
6
10
Po krzyżowaniu otrzymujemy osobniki:
offspring 1
0 1| 1 0 1 1| 0 1 1 1| 1
offspring 2
1 0| 1 1 0 0| 0 0 1 0| 0
39. Krzyżowanie unormowane
Osobniki z 11 binarnymi zmiennymi:individual 1
individual 2
0 1 1 1 0 0 1 1 0 1 0
1 0 1 0 1 1 0 0 1 0 1
Dla każdej zmiennej losujemy osobnika rodzicielskiego z
którego potomek otrzyma wartość binarną. W rezultacie
otrzymujemy dwa słowa binarne o długości 11 dla każdego
osobnika potomnego.
sample 1
sample 2
0 1 1 0 0 0 1 1 0 1 0
1 0 0 1 1 1 0 0 1 0 1
Po krzyżowaniu otrzymamy:
offspring 1
offspring 2
1 1 1 0 1 1 1 1 1 1 1
0 0 1 1 0 0 0 0 0 0 0
40. Inne metody krzyżowania
o krzyżowanie typu tasowanie,o krzyżowanie ze zredukowanym surogatem.
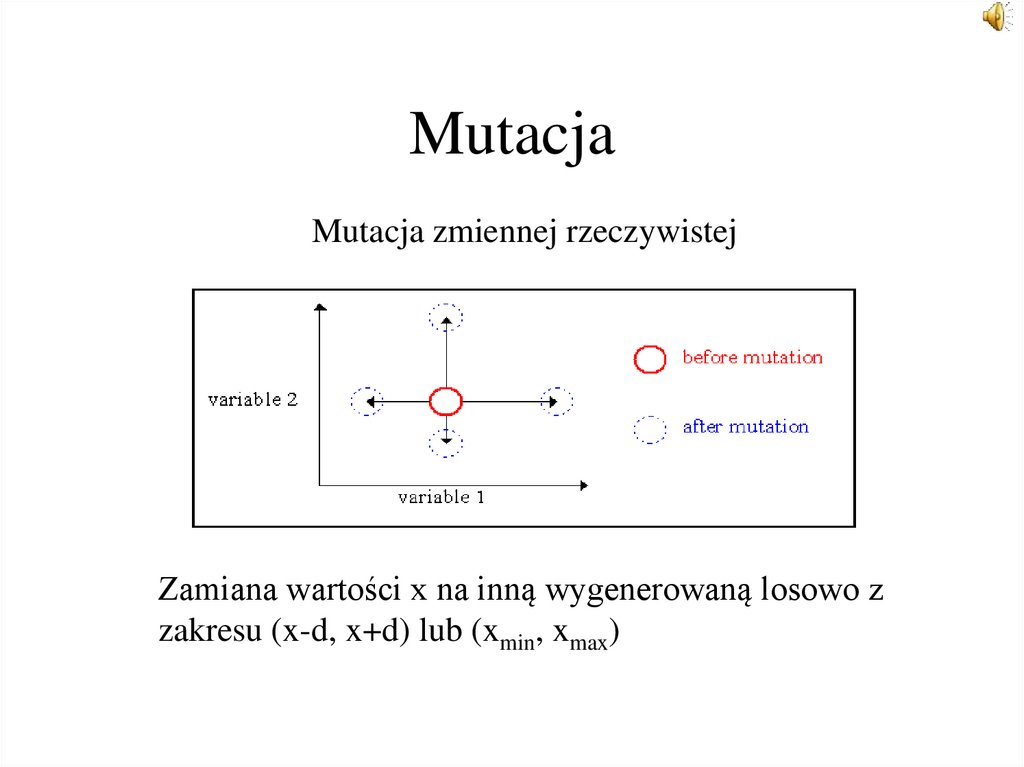
41. Mutacja
Mutacja zmiennej rzeczywistejZamiana wartości x na inną wygenerowaną losowo z
zakresu (x-d, x+d) lub (xmin, xmax)
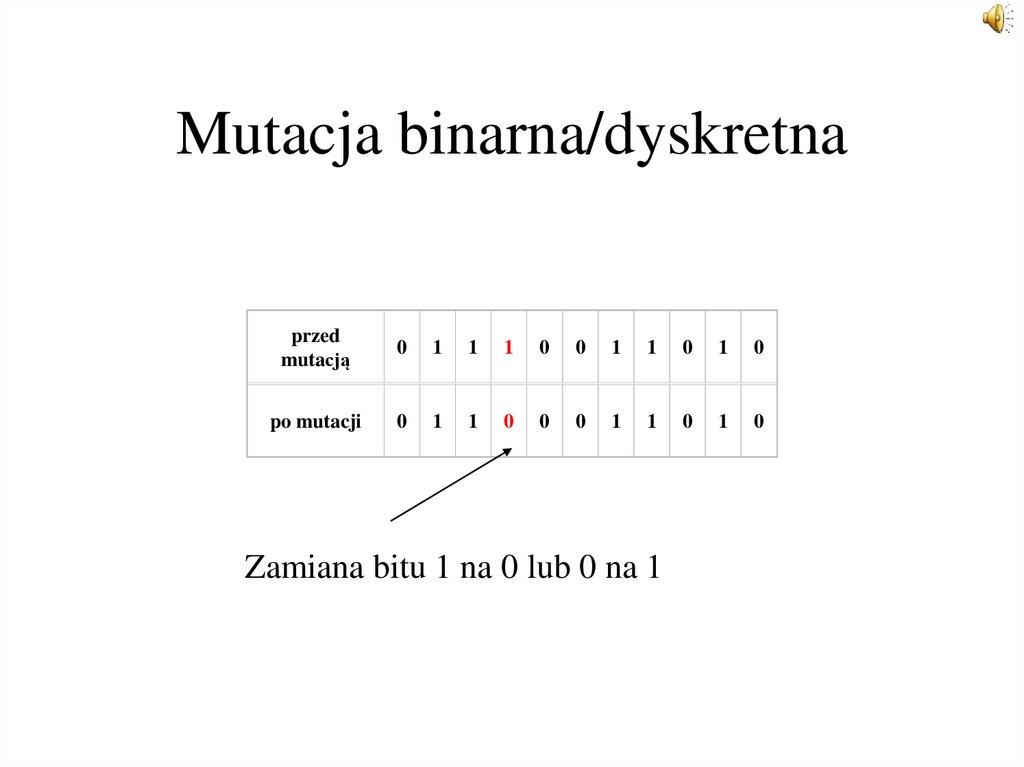
42. Mutacja binarna/dyskretna
przedmutacją
0
1
1
1
0
0
1
1
0
1
0
po mutacji
0
1
1
0
0
0
1
1
0
1
0
Zamiana bitu 1 na 0 lub 0 na 1
43. Tworzenie nowej populacji
• strategia globalna• strategia lokalna
44. Strategia globalna
• wytworzenie takiej samej liczby potomków co osobnikówrodzicielskich i zastąpienie osobników rodzicielskich przez
osobniki potomne (uboga strategia).
• wytworzenie mniejszej liczby potomków niż osobników
rodzicielskich i zastąpienie tych osobników w sposób losowy
jednolity (jednolita strategia).
• wytworzenie mniejszej liczby potomków niż osobników
rodzicielskich i zastąpienie najgorszych osobników osobnikami
potomnymi (elitarna strategia).
• wytworzenie większej liczby potomków niż potrzeba do
zastąpienia osobników rodzicielskich i zastąpienie osobnikami
najlepszymi (strategia oparta na dostosowaniu).
45. Strategia lokalna
W selekcji lokalnej osobniki są dobierane w granicach sąsiedztwa. Strategiawymiany osobników odbywa się dokładnie w tym samym sąsiedztwie.
Występują następujące schematy:
• podmiana wszystkich osobników na osobniki potomne w sposób jednolity
losowy,
• podmiana osobników słabszych sąsiedztwa osobnikami potomnymi,
• wstawienie osobników potomnych lepiej dostosowanych niż najsłabsze
osobniki sąsiedztwa,
• wstawienie osobników potomnych lepiej dostosowanych niż najgorsze
osobniki i podmiana osobników rodzicielskich,
• wstawienie osobników potomnych lepiej dostosowanych niż najgorsze
osobniki i podmiana osobników w sposób jednolity losowy,
• wstawienie osobników potomnych lepiej dostosowanych niż rodzicielskie
oraz ich podmiana.






























 Биология
Биология




