Похожие презентации:
Algorytmy mrówkowe. Algorytmy wzorowane na życiu społecznym mrówek
1.
Algorytmy mrówkoweAlgorytmy wzorowane na życiu społecznym mrówek
Inspiracje biologiczne:
1. Pojedyncza mrówka jest głucha, prawie ślepa, o bardzo małej
inteligencji
2. Mrówki są zwierzętami społecznymi o silnie zarysowanej strukturze
społecznej: królowe, budowniczowie, poszukiwacze pożywienia
3. Owady nie komunikują się ze sobą bezpośrednio
4. Owad poruszając się pozostawia na podłożu ślad feromonowy
5. Mrówki chętniej poruszają się ścieżkami na których ślad
feromonowy jest silniejszy
6. Feromony ulegają parowaniu
2.
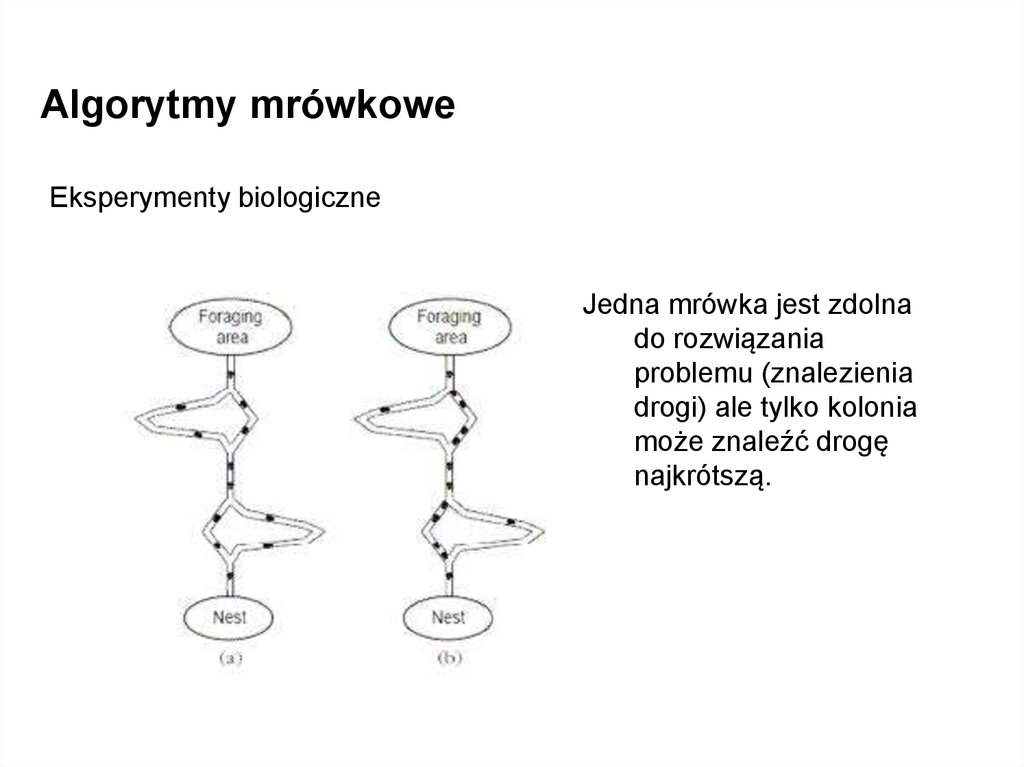
Algorytmy mrówkoweEksperymenty biologiczne
Jedna mrówka jest zdolna
do rozwiązania
problemu (znalezienia
drogi) ale tylko kolonia
może znaleźć drogę
najkrótszą.
3.
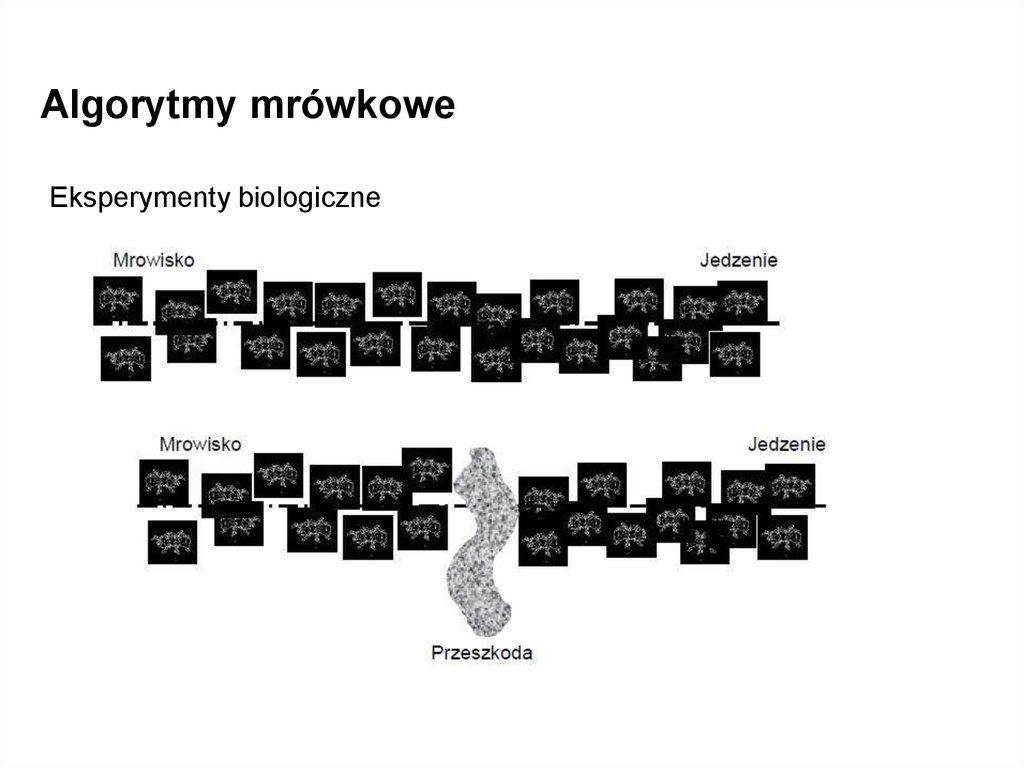
Algorytmy mrówkoweEksperymenty biologiczne
4.
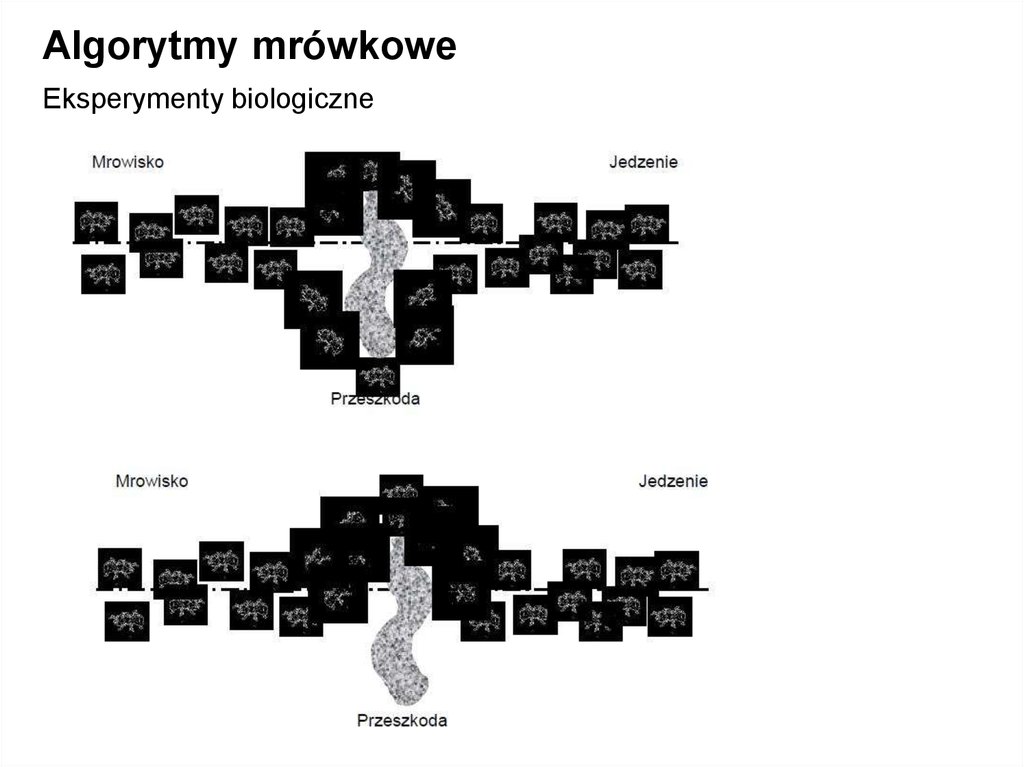
Algorytmy mrówkoweEksperymenty biologiczne
5.
Algorytmy mrówkoweZastosowania algorytmów mrówkowych:
Zadania optymalizacji:
-
problem komiwojażera
problem plecakowy
problem najkrótszej drogi
6.
Algorytmy mrówkoweMrówki w świecie wirtualnym różnią się od mrówek żywych tym, że:
czas w ich świecie nie jest ciągły, a dyskretny (dzięki temu mrówki
pokonują drogę różnej długości w tym samym czasie)
posiadają pamięć, w której zapamiętują np. odwiedzone przez
siebie wierzchołki, bądź krawędzie (w zależności od problemu)
posiadają „wzrok” pozwalający im określić odległość do
najbliższego wierzchołka
feromon nie musi być rozkładany ciągle
7.
Algorytmy mrówkoweMrówki w świecie wirtualnym różnią się od mrówek żywych tym, że:
czas w ich świecie nie jest ciągły, a dyskretny (dzięki temu mrówki
pokonują drogę różnej długości w tym samym czasie)
posiadają pamięć, w której zapamiętują np. odwiedzone przez
siebie wierzchołki, bądź krawędzie (w zależności od problemu)
posiadają „wzrok” pozwalający im określić odległość do
najbliższego wierzchołka
feromon nie musi być rozkładany ciągle
8.
Algorytmy mrówkoweRozkładanie feromonu może być realizowane w sposób:
gęstościowy – mrówki zostawiają stałą ilość feromonu podczas
budowania drogi
ilościowy - mrówki zostawiają ilość feromonu odwrotnie
proporcjonalną do długości wybranej krawędzi podczas budowania
drogi
cykliczny - mrówki zostawiają feromon dopiero po zbudowaniu całej
drogi
Algorytm wykorzystujący cykliczny sposób rozkładania feromonu
nazywamy Systemem Mrówkowym.
9.
System mrówkowyW algorytmie tym m mrówek buduje drogi. Początkowo mrówki
wybierają wierzchołki zupełnie losowo. W każdym kroku
konstruowania drogi mrówka k dokonuje wyboru, który wierzchołek
odwiedzić jako następny.
Prawdopodobieństwo, ze mrówka znajdująca się w wierzchołku i
wybierze ruch do wierzchołka j określamy następującą zależnością:
gdzie:
τij – oznacza ilość feromonu na krawędzi łączącej wierzchołki i oraz j
ηij – oznacza wartość heurystyczną, czyli liczbę określającą atrakcyjność wyboru danej drogi
α, β – dwa parametry, które określają względny wpływ ilości feromonu i wartości heurystycznej na
wybór dokonywany przez mrówkę
i
N k - lista miast sąsiedztwa, do których się może bezpośrednio przenieść mrówka k będąc w mieście i
10.
System mrówkowyKażda mrówka posiada pamięć, w której zapisuje wierzchołki, które już
odwiedziła i kolejność ich odwiedzenia.
Pamięć ta jest używana do określenia dostępnego sąsiedztwa i pozwala
mrówce k obliczyć długość trasy jaką przebyła, aby wiedzieć ile
feromonu powinna ona na niej odłożyć.
Po tym, jak wszystkie mrówki przebędą swoje trasy, algorytm uaktualnia
ilość feromonu na ścieżkach.
Najpierw zmniejsza ilość feromonu (parowanie) zgodnie z zależnością:
gdzie 0< <1 jest współczynnikiem parowania feromonu.
11.
System mrówkowyPo parowaniu wszystkie mrówki pozostawiają feromon na krawędziach
które przeszły podczas swojej drogi zgodnie z zależnością:
gdzie Δ kij to ilość feromonu mrówki k który pozostawia na krawędzi,
którą odwiedziła.
Im lepsza jest droga mrówki k, tym więcej feromonu pozostanie na
krawędziach należących do tej drogi.
Ogólnie krawędzie które zostały użyte przez większą liczbę mrówek
wybierających krótsze trasy, dostaną więcej feromonu i przez to
będą wybierane częściej w przyszłych iteracjach.
12.
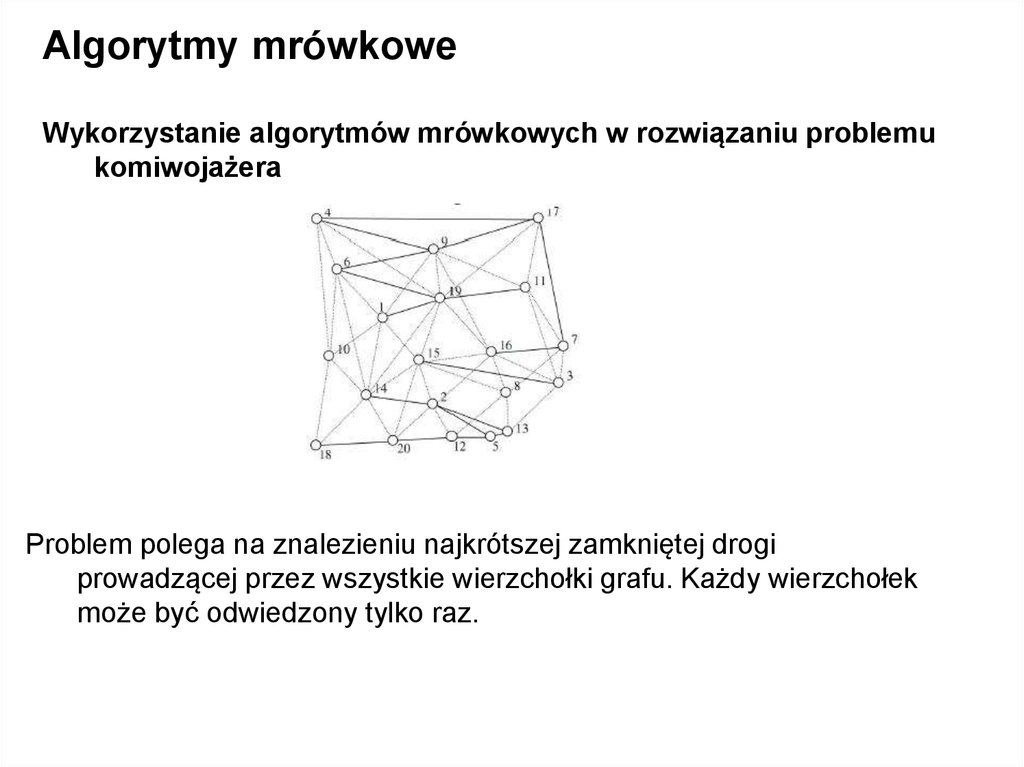
Algorytmy mrówkoweWykorzystanie algorytmów mrówkowych w rozwiązaniu problemu
komiwojażera
Problem polega na znalezieniu najkrótszej zamkniętej drogi
prowadzącej przez wszystkie wierzchołki grafu. Każdy wierzchołek
może być odwiedzony tylko raz.
13.
Algorytmy mrówkoweWykorzystanie algorytmów mrówkowych w rozwiązaniu problemu
komiwojażera
Liczba rozwiązań problemu:
4 miasta l = 3
10 miast l = 181440
50 miast l to około 1061
14.
Algorytmy mrówkoweWykorzystanie algorytmów mrówkowych w rozwiązaniu problemu
komiwojażera
Działanie algorytmu:
1. Tworzona jest populacja mrówek. Jej rozmiar jest jednym z
parametrów algorytmu.
2. Pojedyncza mrówka generuje swoją ścieżkę niezależnie od swoich
towarzyszek.
3. Dla każdej mrówki generowane jest losowo miasto, z którego ma
rozpocząć wędrówkę.
4. Mrówka porusza się po grafie, szukając sekwencji wierzchołków
grafu tworzącej najkrótszą drogę od wierzchołka startowego do
końcowego.
15.
Algorytmy mrówkoweWykorzystanie algorytmów mrówkowych w rozwiązaniu problemu
komiwojażera
Działanie algorytmu:
5. Aby nie wracać do już odwiedzonych wierzchołków, mrówka jest
wyposażona w pamięć, w której przechowuje listę takich
wierzchołków. Na starcie lista jest pusta, a po dojściu do celu
zawiera wierzchołki w kolejności ich odwiedzenia.
6. Mrówka rusza z miasta startowego i dochodząc do każdego
kolejnego miasta pozostawia na krawędzi grafu feromon. Na
początku algorytmu wszystkie ścieżki otrzymują początkową
wartość feromonu.
7. Wybór kolejnego odcinka drogi jest losowy, ale zgodny z zasadą –
im więcej feromonu na danej krawędzi grafu, tym większe
prawdopodobieństwo wyboru tej drogi przez mrówkę.
16.
Algorytmy mrówkoweWykorzystanie algorytmów mrówkowych w rozwiązaniu problemu
komiwojażera
Działanie algorytmu:
8. Algorytm ma iteracyjny charakter – po zakończeniu bieżącej iteracji
każda mrówka czeka na wyznaczenie nowego miasta
początkowego, skąd w następnej iteracji ponownie wyruszy, by
przemierzać swoją trasę.
9. Istotny jest efekt gromadzenia się feromonu na krawędziach grafu w
miarę upływu czasu (kolejnych iteracji).
10. W miarę upływu czasu pozostawiony feromon paruje, przez co
zmniejsza się jego ilość na ścieżkach.
11. Najważniejszym elementem algorytmu przechowującym informacje
o rozwiązaniu jest struktura zawierająca wartości poziomu feromonu
na poszczególnych krawędziach.
17.
Systemy rojoweAlgorytmy oparte na zachowaniu roju pszczół
Inspiracje biologiczne:
Zaobserwowano, że rój pszczół miodnych potrafi znaleźć i optymalnie
wykorzystać najlepsze jakościowo i najbogatsze źródła pożywienia
w okolicy ula.
Pszczoły potrafią znakomicie dostosować się do zmieniających się
warunków środowiskowych.
Optymalizacja zachowania roju jest możliwa dzięki specjalizacji grup
pszczół oraz specyficznemu sposobowi porozumiewania się (taniec
pszczół).
18.
Systemy rojoweInspiracje biologiczne:
Pszczoły w roju są podzielone na następujące grupy biorące udział w
poszukiwaniu pożywienia:
Zwiadowca – w sposób losowy przeszukuje teren w celu odnalezienia
nektaru
Pszczoła bezrobotna – zostaje zwerbowana tańcem innej pszczoły lub
zostaje zwiadowcą
Pracująca zbieraczka – zna obfite źródło pożywienia i korzysta z niego
transportując je do ula
Doświadczona zbieraczka – ma wiedzę (również historyczną) o jakości oraz
miejscu gdzie znajduje się nektar. Wykonuje ona poniższe cele:
rekrut – rozpoczyna poszukiwanie nowego źródła pożywienia ponieważ
nie odpowiada mu obecnie odwiedzone
zwiadowca – przeszukuje teren by odnaleźć nowe źródło pożywienia
po odnalezieniu poprzedniego
furażerka zrekrutowana – na podstawie areny tanecznej rozpatruje to
samo źródło pokarmu
inspektor – sprawdza jakość odkrytego pokarmu
19.
Systemy rojoweInspiracje biologiczne:
Zwiadowca po znalezieniu źródła pożywienia wraca do ula z próbką.
Za pomocą tańca przekazuje innym pszczołom informacje o lokalizacji i
jakości źródła.
Kierunek w którym tańczy pszczoła (wykonuje ruch na wprost) określa kąt pomiędzy
zlokalizowanym pożywieniem a słońcem.
Dystans pomiędzy ulem a źródłem pokarmu jest kodowany przez pszczołę za pomocą
czasu trwania ruchu wykonywanego na wprost w tańcu.
Jakość nektaru określa wielkość odchylenia ciała pszczoły tworząc wibrację. Im większe
tym lepsza jakość pożywienia.
20.
Systemy rojoweAlgorytm poszukiwania pokarmu przez pszczoły
1. Zwiadowcy zaczynają poszukiwać losowo pożywienia przechodząc
kolejno z jednego źródła do drugiego.
21.
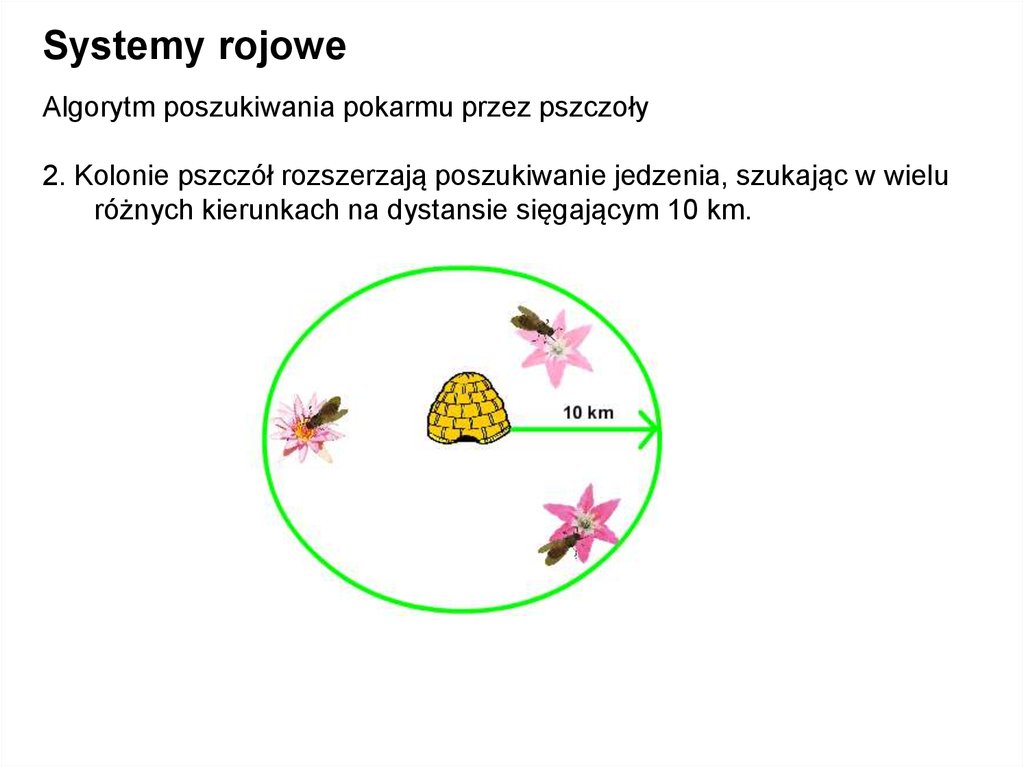
Systemy rojoweAlgorytm poszukiwania pokarmu przez pszczoły
2. Kolonie pszczół rozszerzają poszukiwanie jedzenia, szukając w wielu
różnych kierunkach na dystansie sięgającym 10 km.
22.
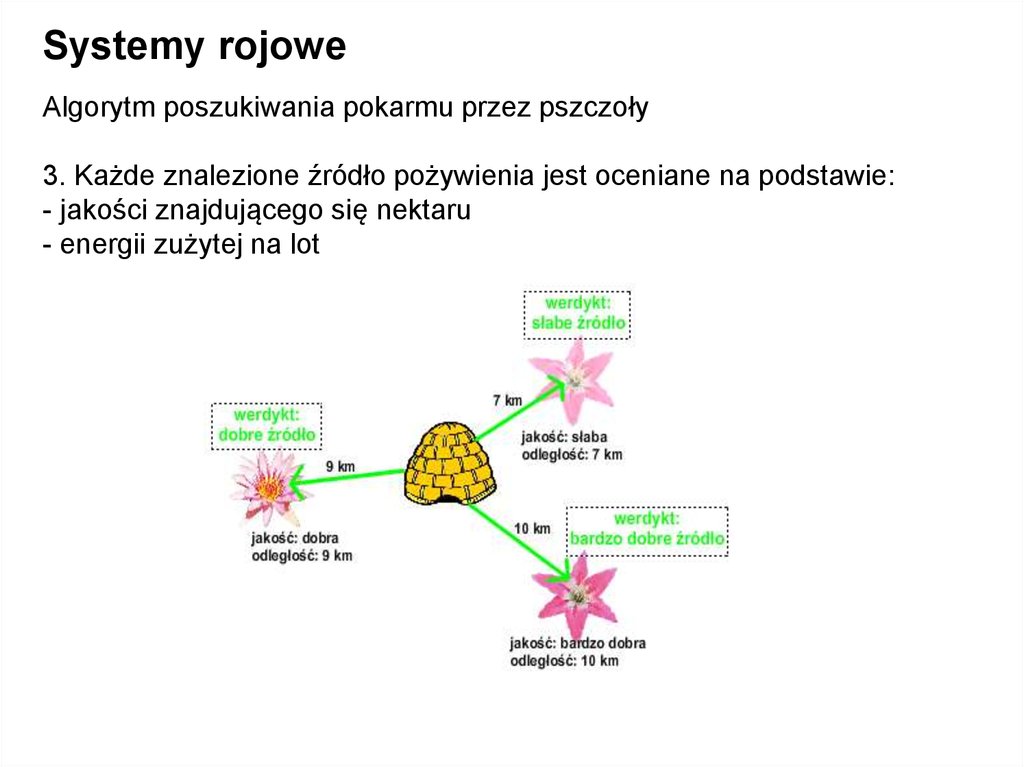
Systemy rojoweAlgorytm poszukiwania pokarmu przez pszczoły
3. Każde znalezione źródło pożywienia jest oceniane na podstawie:
- jakości znajdującego się nektaru
- energii zużytej na lot
23.
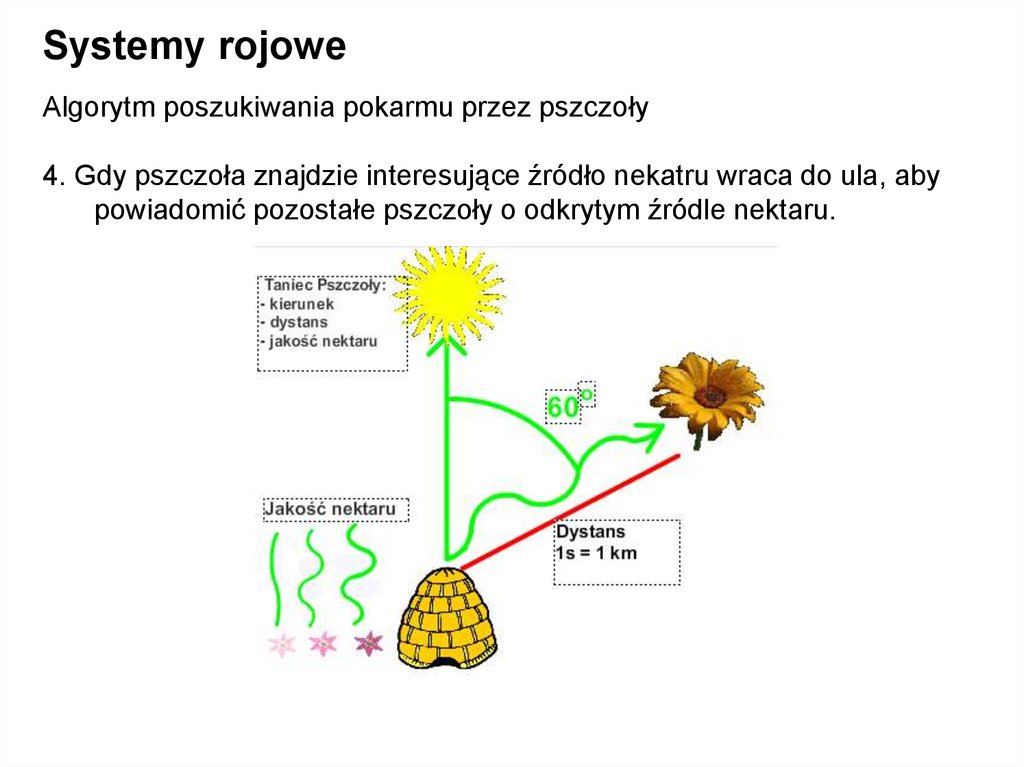
Systemy rojoweAlgorytm poszukiwania pokarmu przez pszczoły
4. Gdy pszczoła znajdzie interesujące źródło nekatru wraca do ula, aby
powiadomić pozostałe pszczoły o odkrytym źródle nektaru.
24.
Systemy rojoweAlgorytm poszukiwania pokarmu przez pszczoły
5. Najlepsze źródła pożywienia zostają odwiedzone przez największą
liczbę pszczół. Źródła zawierające niską jakość nektaru, bądź
znajdujące się zbyt daleko od ula często nie są odwiedzane przez
żadne pszczoły.
25.
Systemy rojowePrzykłady algorytmów
Artificial Bee Colony (ABC)
Algorytm opracowany w 2005 roku przez Dervis Karaboga
Wraz z upływem czasu sztuczne pszczoły odkrywają źródła pokarmu z
większą ilością nektaru, by w końcu wybrać najlepsze. W systemie
ABC sztuczne pszczoły latają w trójwymiarowej przestrzeni
poszukiwań, a niektóre (pracujące i obserwujące pszczoły)
wybierają źródła żywności na podstawie doświadczenia własnego
oraz kolegów z gniazda. Zwiadowcy natomiast zbierają nektar z
losowo wybranych źródeł, bez użycia doświadczenia. Jeśli ilość
nektaru w nowym źródle jest wyższa niż w poprzednich
zapamiętanych w pamięci, wtedy pszczoła zapamiętuje nowe
miejsce, zapominając jednocześnie o poprzednich.
26.
Systemy rojowePrzykłady algorytmów
Artificial Bee Colony (ABC)
Pseudokod algorytmu ABC:
27.
Systemy rojowePrzykłady algorytmów
Bee Colony Optimization (BCO)
Algorytm opracowany w 2005 roku przez D. Teodorovic i M. Dell′Orco
Konstrukcja rozwiązania końcowego tworzona jest przez rozwijanie
rozwiązań częściowych, mierne rozwiązania odrzucane są już na
etapie ich konstrukcji. O każdym rozwiązaniu można myśleć jak o
ścieżce z roju do źródła pożywienia.
28.
Systemy rojowePrzykłady algorytmów
Bee Colony Optimization (BCO)
Pseudokod algorytmu BCO:
29.
Systemy rojoweWykorzystanie algorytmów pszczelich:
Optymalizacja pracy serwerów (grup serwerów)
Optymalizacja procesów przemysłowych i biznesowych (alokacja
środków przedsiębiorstwa)




















 Биология
Биология

