Похожие презентации:
Основы теории вероятностей. (Лекция 1)
1. Основы теории вероятностей
16.05.16Харламова Ирина Юрьевна
2. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
1. Общие правила комбинаторики.2. Выборки элементов.
3. Выборки элементов с повторениями.
Харламова Ирина Ю
16.05.16
3. Комбинаторика –
область математики, в которой изучаютсявопросы о том, сколько различных
комбинаций, подчиненных тем или иным
условиям, можно составить из элементов,
принадлежащих заданному множеству.
Харламова Ирина Ю
16.05.16
4.
Комбинаторика возникла в XVI веке. В жизнипривилегированных слоев тогдашнего общества
большое место занимали азартные игры.
5. Теоретические исследования вопросов комбинаторики предприняли в XVII веке французские ученые
Теоретические исследованиявопросов комбинаторики
предприняли в XVII веке французские
ученые
Пьер Ферма
(1601-65)
Блез Паскаль
(1623-62)
6.
ЯковБернулли
(1654-1705)
Готфрид
Лейбниц
(1646-1716)
Леонард
Эйлер
(1707-1783)
7. 1 ?
1?ОБЩИЕ ПРАВИЛА
КОМБИНАТОРИКИ
16.05.16
Харламова Ирина Юрьевна
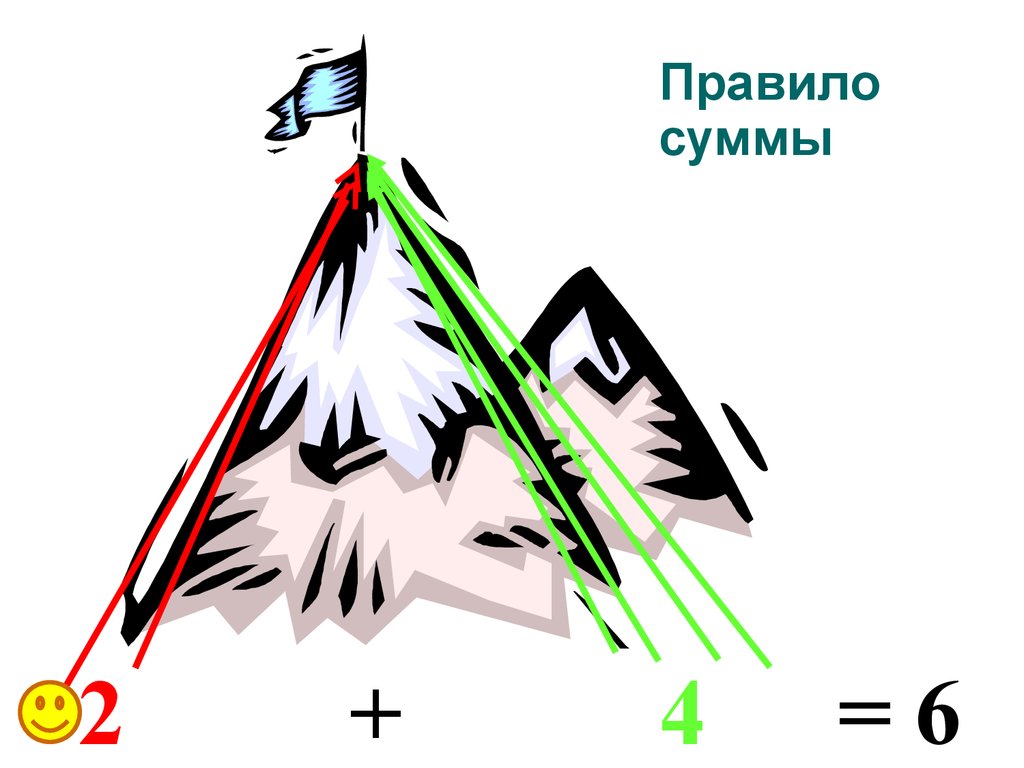
8. ПРАВИЛО СУММЫ
Если некоторый объект А можно выбратьm способами, а другой объект В можно
выбрать k способами, то выбор
«либо А, либо В»
можно осуществить m+k способами.
Харламова Ирина Ю
16.05.16
9. ТУРЦИЯ
1ТУРЦИЯ
3
2
10. ЕГИПЕТ
12
11.
11
2
2
3
3 +2 =5
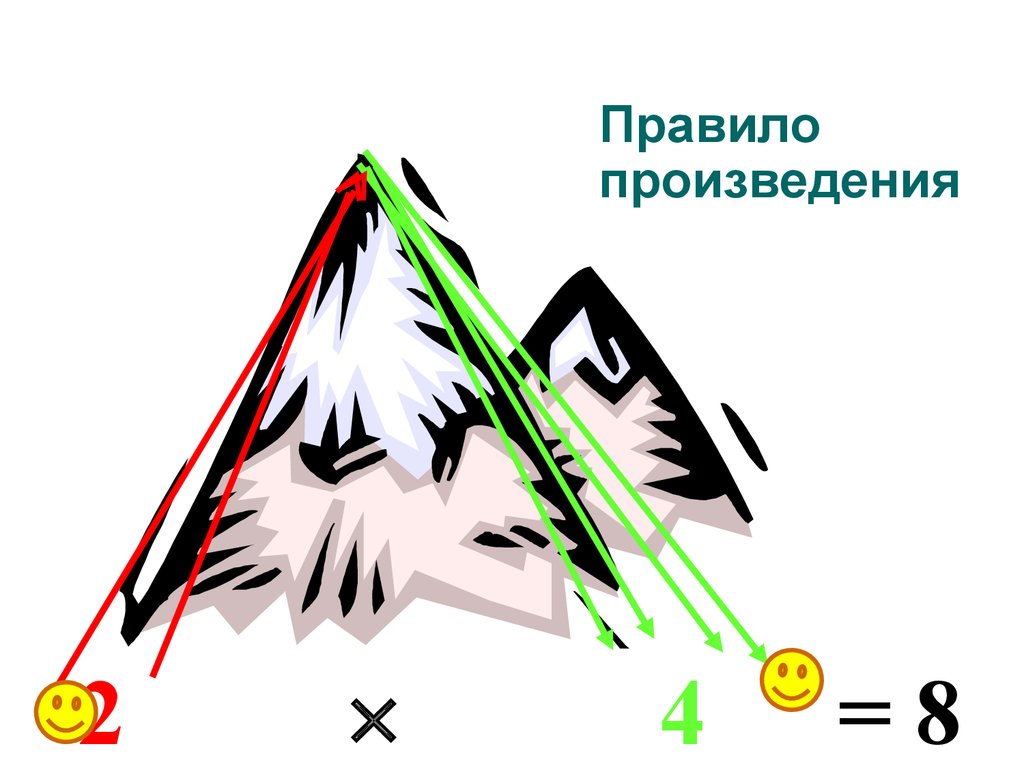
12. ПРАВИЛО ПРОИЗВЕДЕНИЯ
Если объект А можно выбрать m способами, иесли после каждого такого выбора объект В
можно выбрать k способами, то выбор пары
объектов
АиВ
в указанном порядке можно осуществить
m k способами.
Харламова Ирина Ю
16.05.16
13.
1ТУРЦИЯ
3
2
14.
ЕГИПЕТ1
2
15.
21
3
1
2
2
3
1
2 3= 6
16.
12
3
1
1
1
1
2
3
2
2
2
17. Правило суммы
2+
4
=6
18.
45632119. Правило произведения
24
=8
20.
4713658221. 2? Выборки элементов
РазмещенияСочетания
Перестановки
16.05.16
Харламова Ирина Юрьевна
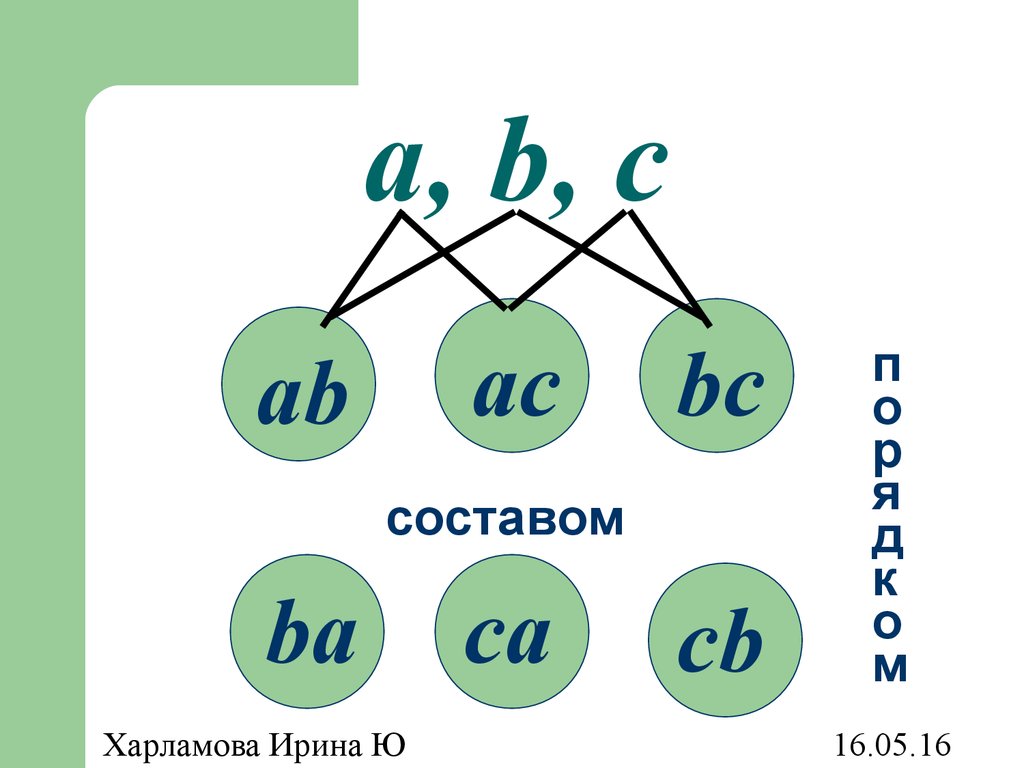
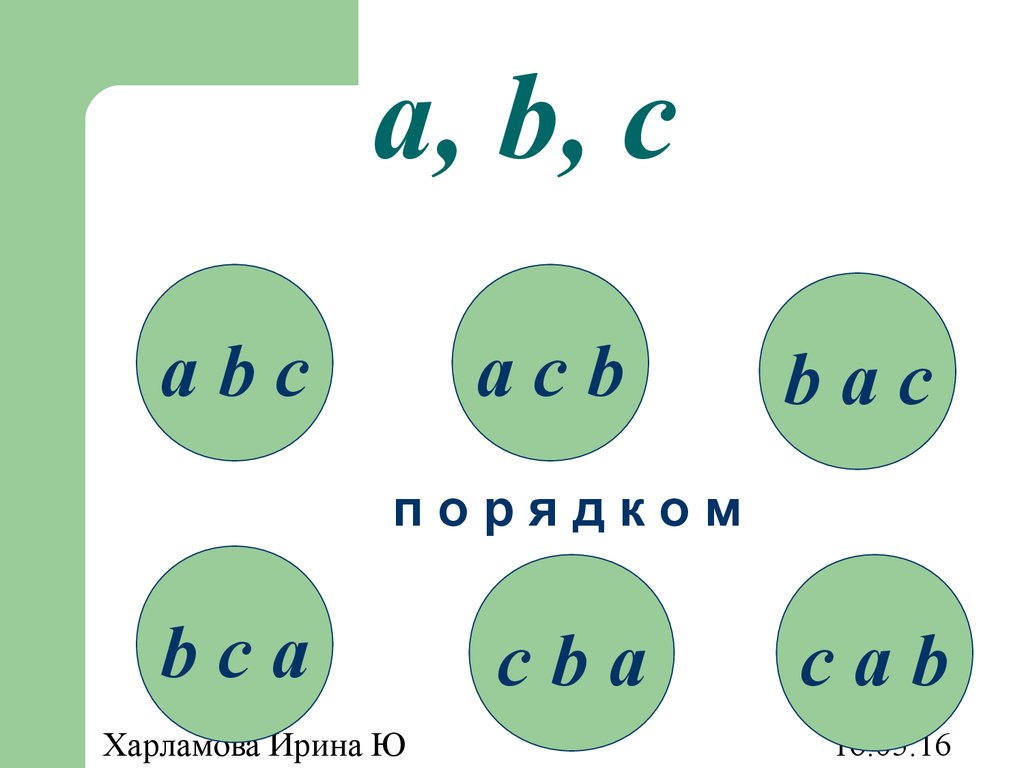
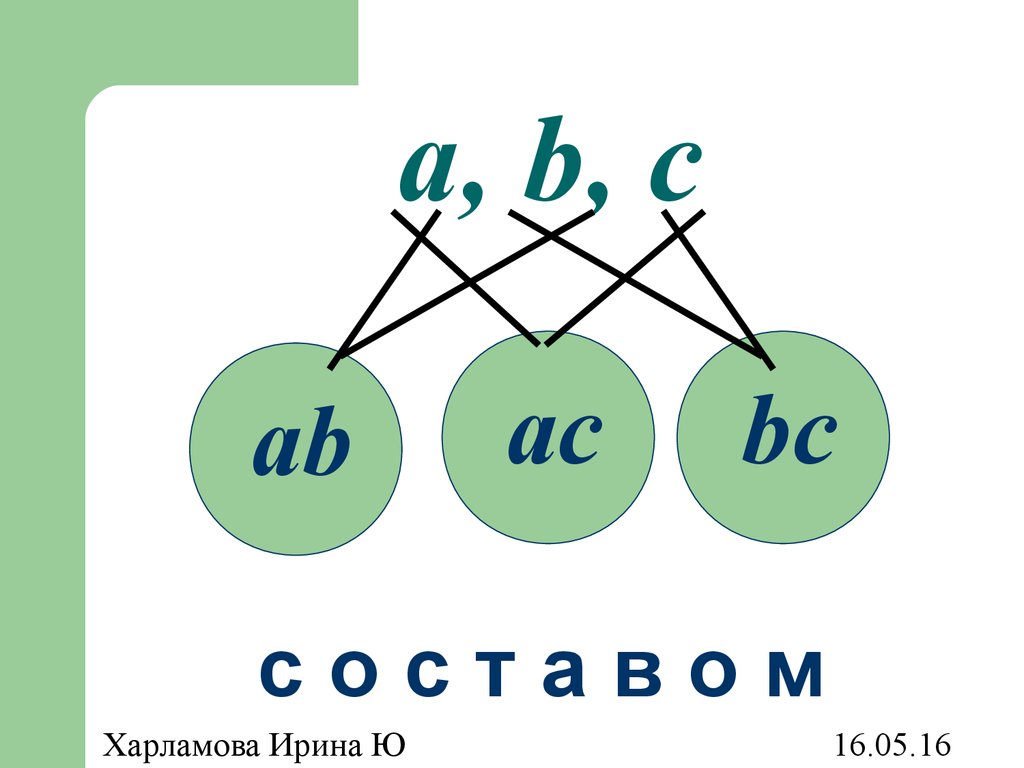
22. Размещения
Размещениями из n элементов по kназываются такие выборки, которые,
имея по k различных элементов,
выбранных из числа данных n,
отличаются одна от другой либо
составом элементов, либо порядком
их расположения.
Харламова Ирина Ю
16.05.16
23. a, b, c
acab
bc
составом
ba
Харламова Ирина Ю
ca
cb
п
о
р
я
д
к
о
м
16.05.16
24. Число размещений из n элементов по k
n!
k
An
(n k )!
1 2 3 ... n, если n 0;
n!
если n 0.
1,
Харламова Ирина Ю
16.05.16
25. Число размещений из 3 элементов по 2
3!A
(3 2)!
2
3
3! 1 2 3
6
1!
1
Харламова Ирина Ю
16.05.16
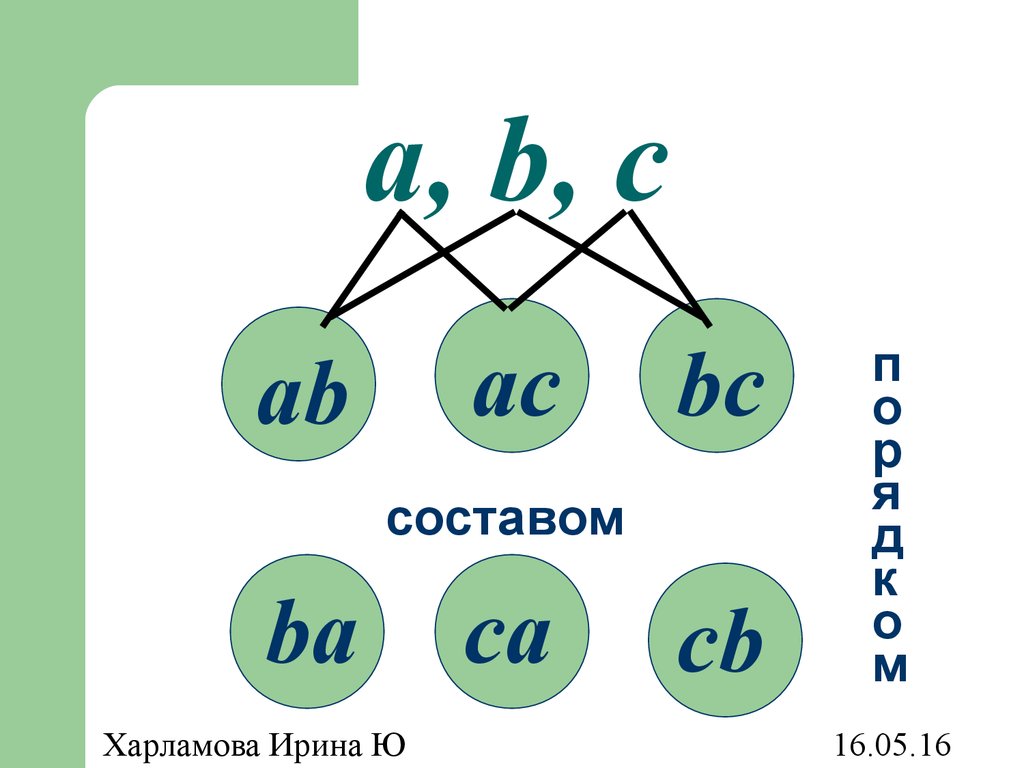
26. a, b, c
acab
bc
составом
ba
Харламова Ирина Ю
ca
cb
п
о
р
я
д
к
о
м
16.05.16
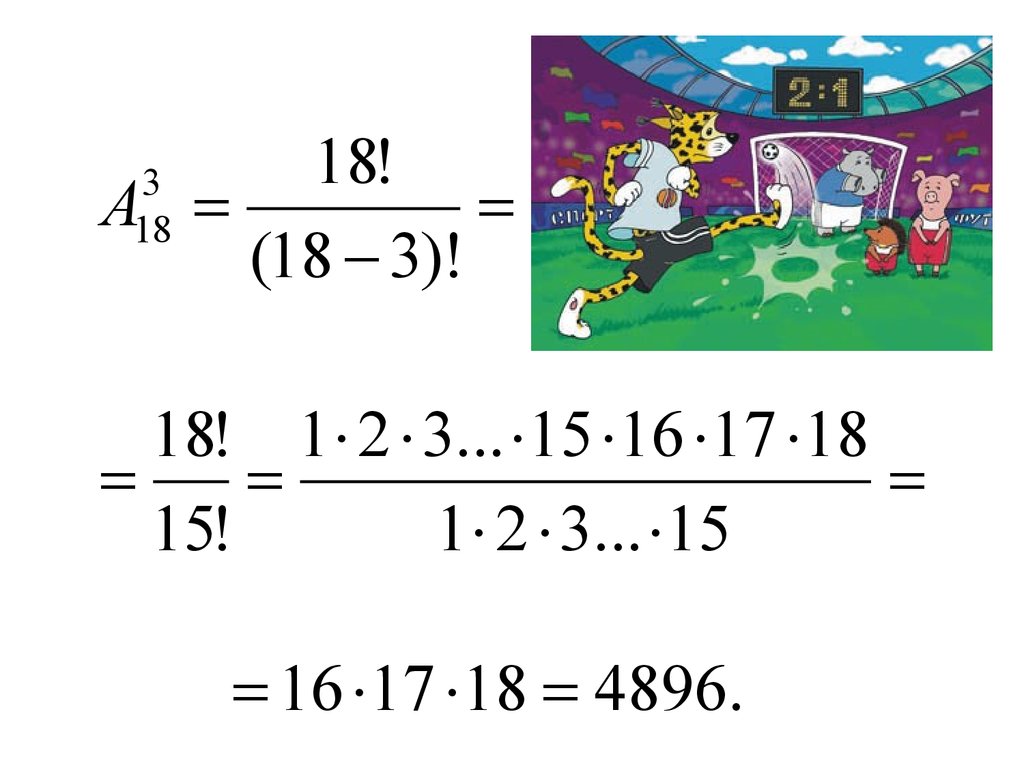
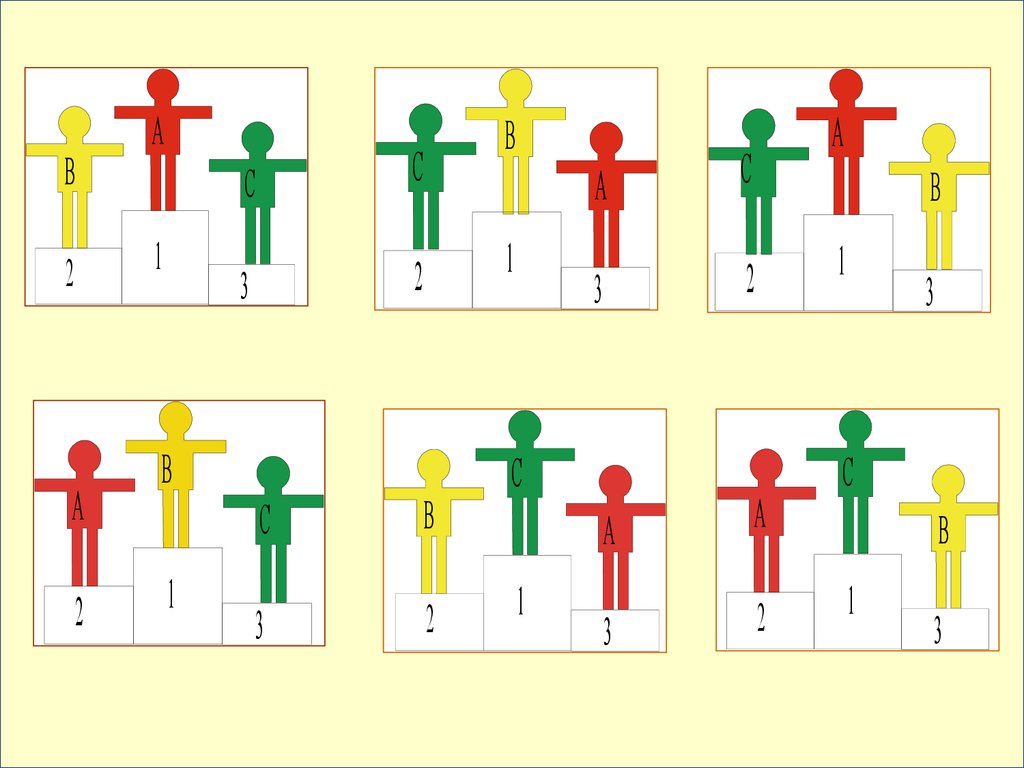
27.
В турнире по футболу участвуют18 команд. Борьба идет за золотые,
серебряные и бронзовые медали.
Сколькими способами медали
могут быть распределены между
командами?
28.
A B C D E FG
K
L
M N O P Q R
J
H
I
29.
AB
1
2
A
2
D
2
C
C
3
2
1
B
1
C
B
3
2
C
1
B
A
C
3
2
A
C
3
2
C
1
B
A
A
3
2
D
1
A
A
D
3
2
1
3
C
B
1
3
C
B
1
3
30.
18!A
(18 3)!
3
18
18! 1 2 3... 15 16 17 18
15!
1 2 3... 15
16 17 18 4896.
31. n=k
Соответствующиеэтому
случаю размещения называют
перестановками.
Харламова Ирина Ю
16.05.16
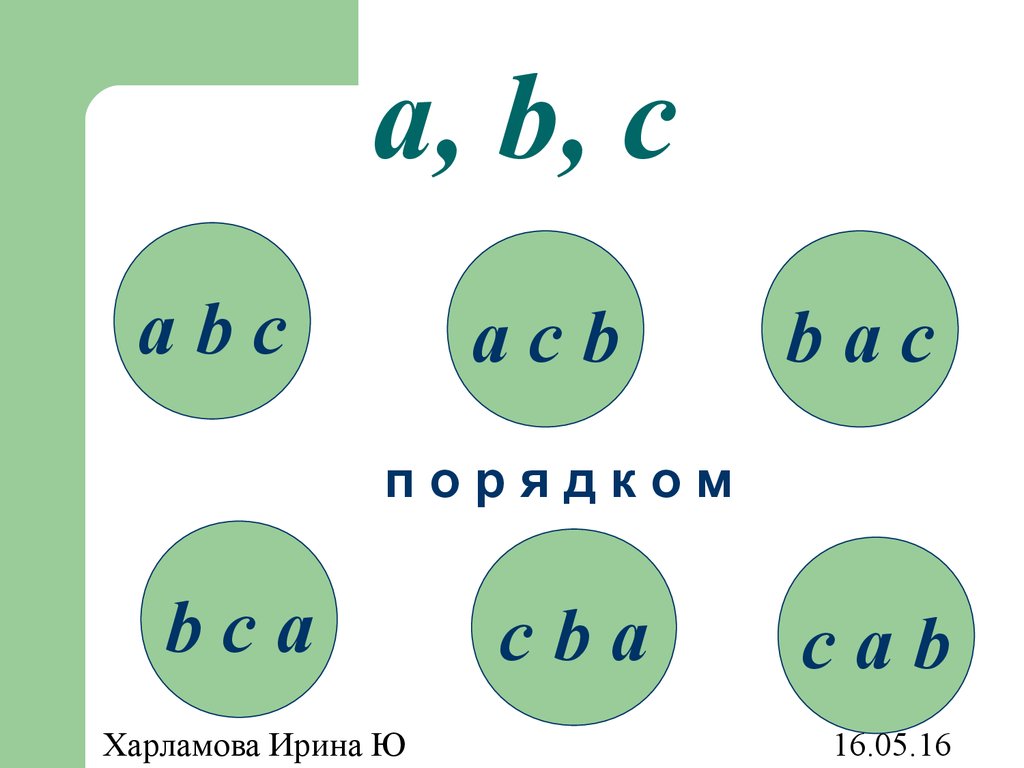
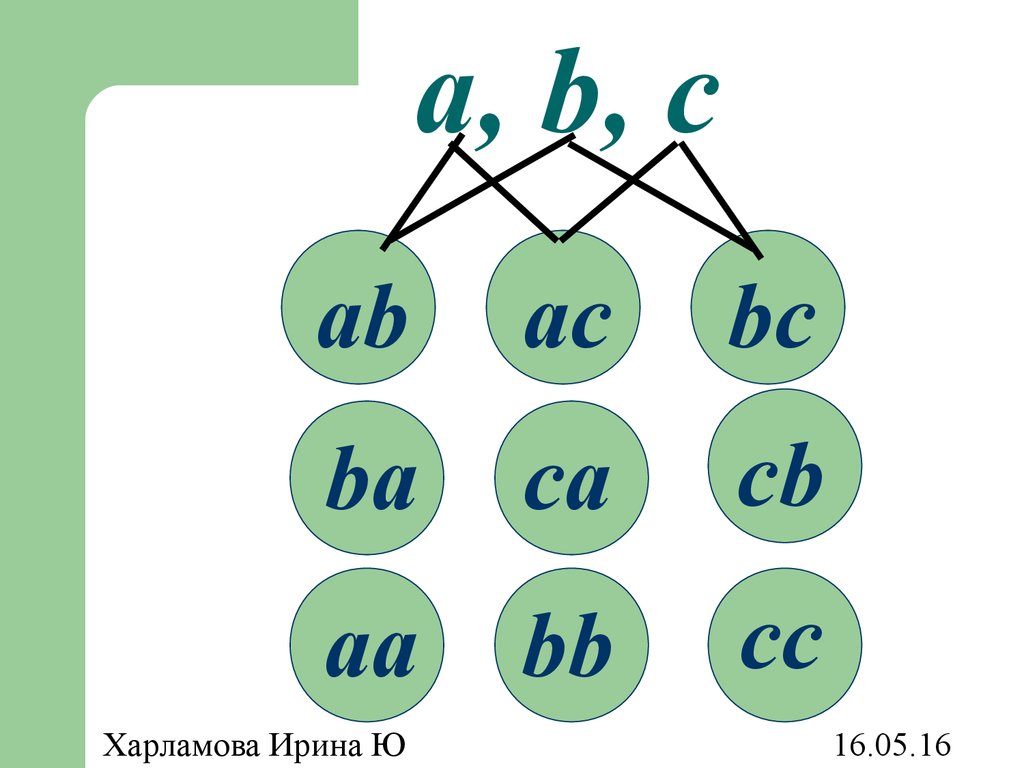
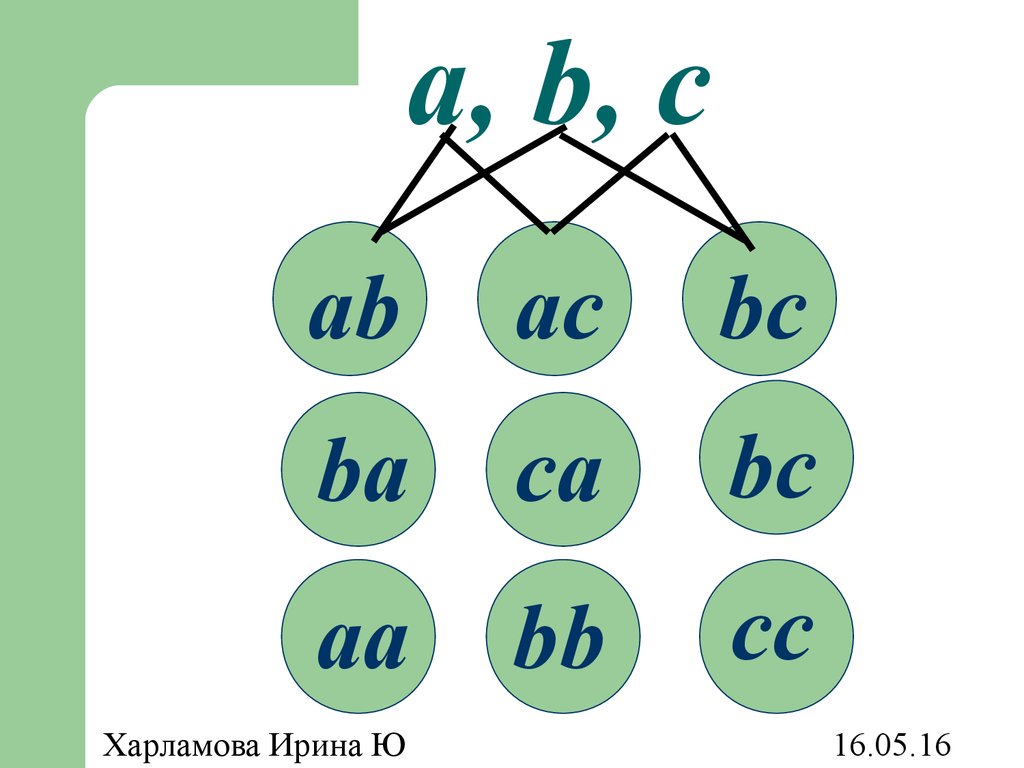
32. Перестановки
Перестановками из n элементовназываются
такие
выборки,
которые, имея по n различных
элементов, отличаются одна от
другой лишь порядком следования
этих элементов.
Харламова Ирина Ю
16.05.16
33. a, b, c
abсaсb
baс
порядком
bсa
Харламова Ирина Ю
сba
сab
16.05.16
34. Число перестановок из n элементов
n!Pn A
(n n)!
n! n!
n!
0! 1
n
n
Харламова Ирина Ю
16.05.16
35. Число перестановок из n элементов
Pn n!Харламова Ирина Ю
16.05.16
36. Число перестановок из 3 элементов
P3 3!1 2 3 6
Харламова Ирина Ю
16.05.16
37. a, b, c
abсaсb
baс
порядком
bсa
Харламова Ирина Ю
сba
сab
16.05.16
38.
AB
1
2
A
2
C
C
3
2
B
1
B
C
1
3
B
2
A
C
3
2
C
1
A
B
1
A
A
3
2
3
C
B
1
3
39. Сколько перестановок можно сделать из букв слова
40.
т юир сюр
с ют ир юр
т
ю
т
с
ю
р
р
с
и
р
ю
р
и
ю
ю ри с т
ию
юю
р
ри с т ю
рс т р
ю
р
и
ю
ри
ю
с
т
с
т
р
р
ю
и
ю
41. Число перестановок из 5 элементов
P5 5!1 2 3 4 5
120
Харламова Ирина Ю
16.05.16
42. Сочетания
Сочетаниями из n элементов по kназываются такие выборки, которые,
имея по k различных элементов,
выбранных из числа данных n,
отличаются только составом элементов
(порядок расположения элементов
значения не имеет).
Харламова Ирина Ю
16.05.16
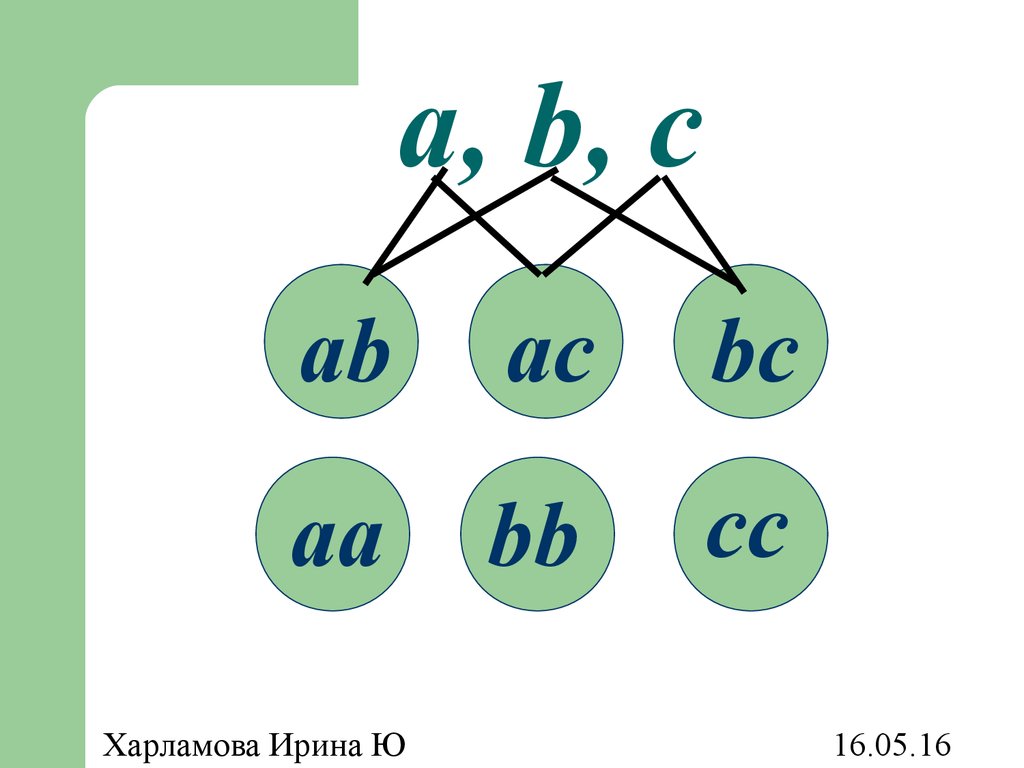
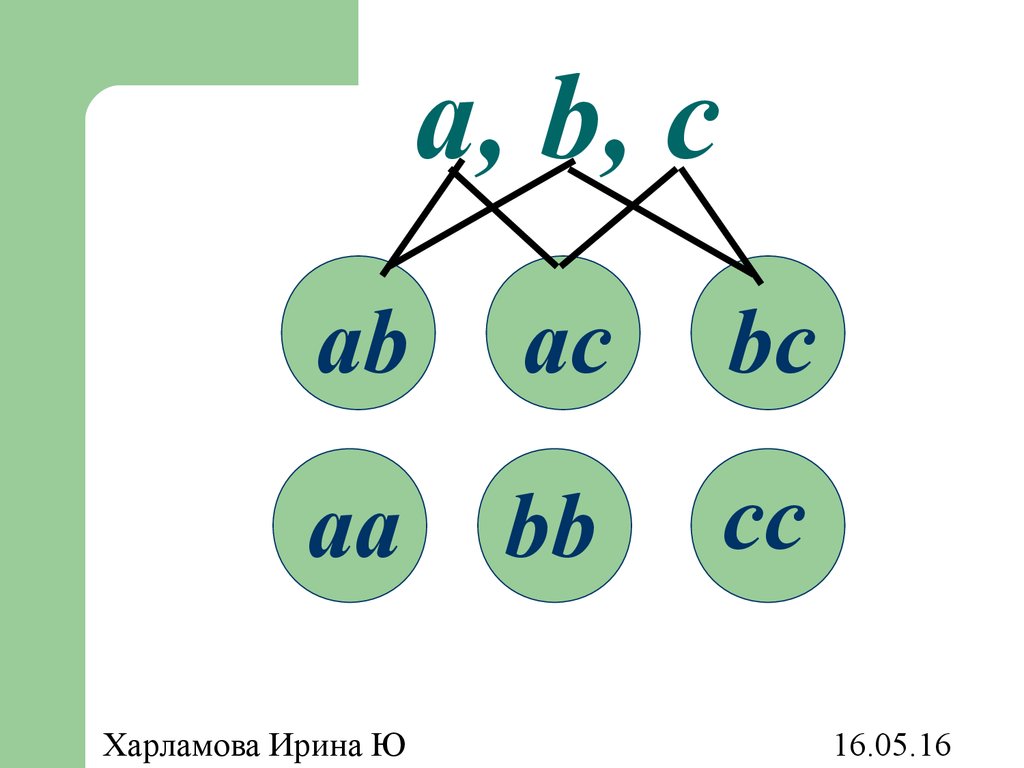
43. a, b, c
abac
bc
составом
Харламова Ирина Ю
16.05.16
44. Число сочетаний из n элементов по k
n!
k
Cn
k! (n k )!
Харламова Ирина Ю
16.05.16
45. Число сочетаний из 3 элементов по 2
3!C
2! (3 2)!
k
n
3! 1 2 3
3
2! 1! 1 2
Харламова Ирина Ю
16.05.16
46. На тренировке занимаются 15 баскетболистов. Сколько может быть образовано тренером разных стартовых пятерок?
47. Число сочетаний из 15 элементов по 5
15!C
5! (15 5)!
5
15
15! 11 12 13 14 15
5! 10!
1 2 3 4 5
3003
48. 3? Выборки с повторениями
Размещенияс повторениями
Сочетания с повторениями
Перестановки с повторениями
16.05.16
Харламова Ирина Юрьевна
49. Размещения с повторениями из n элементов по k
Размещениями с повторениями из nэлементов по k называются такие выборки,
которые, имея по k элементов, выбранных
из числа данных n элементов, отличаются
одна от другой либо составом элементов,
либо порядком их расположения, причем
один и тот же элемент может входить в
выборку более одного раза.
Харламова Ирина Ю
16.05.16
50. a, b, c
abac
bc
ba
ca
cb
aа
bb
cc
Харламова Ирина Ю
16.05.16
51. Число размещений с повторениями из n элементов по k
~kk
An n
Харламова Ирина Ю
16.05.16
52. Число размещений с повторениями из 3 элементов по 2
~22
A3 3 9
Харламова Ирина Ю
16.05.16
53. a, b, c
abac
bc
ba
ca
bc
aа
bb
cc
Харламова Ирина Ю
16.05.16
54. Код Морзе
Самуэль Морзе(1791-1872)
При передачи сообщений по
телеграфу используется код
Морзе. В этом коде буквы,
цифры и знаки препинания
обозначаются точками и тире.
Можно ли передавать
сообщение с помощью четырех
знаков?
55.
С помощью одногознака можно передать
только
2 буквы:
С помощью двух
знаков можно
передать 4 буквы:
•
•–
Е • и Т–
~2
2
A2 2 4
–
– –
56.
С помощью трехзнаков можно
передать 8 букв:
С помощью
четырех знаков
можно передать 16
букв:
~3
3
A2 2 8
~4
4
A2 2 16
Общее число букв, которые можно
передать четырьмя знаками :
2+4+8+16=30
57.
В русском алфавите 33 буквы, такженадо передавать цифры и знаки
препинания .
Следовательно, 4 знаков не хватит.
~5
5
A2 2 32
30+32=62
Э••–•
58. Перестановки с повторениями
Перестановки, в которых хотьодин элемент встречается более
одного раза, называются
перестановками с повторениями.
Харламова Ирина Ю
16.05.16
59. в которых есть n1 элементов одного вида, n2 элементов другого вида и т.д.
Число перестановок сповторениями из n
элементов,
в которых есть n1 элементов
одного
вида, n2 элементов другого вида и т.д.
~
Pn (n1 , n2 ,..., nk )
n!
n1! n2 ! ... nk !
n1 n2 ... nk n
Харламова Ирина Ю
16.05.16
60. Сколько перестановок можно сделать из букв слова
61.
ПРОКУРОРПРОКУРОР
ПРОКУРОР
ПР
КУРОР
КОР
62.
n=8: ПРОКУРОРП n1=1
Р n2=3
О n3=2
К n4=1
У n =1
63.
8!P8 (1,3,2,1,1)
1! 3! 2! 1! 1!
3360
1 3 2 1 1 8
64. АНАГРАММЫ
До XVII столетияпочти не было
научных журналов.
Ученые узнавали о
трудах своих коллег
или из книг, или из
частных писем.
65. АРХИМЕД (ок. 287 – 212 до н.э.)
66. АНАГРАММЫ
НАСОСХарламова Ирина Ю
СОСНА
16.05.16
67.
aaaaaaa, ccccc, d,eeeee, g, h, iiiiiii, lll,
mm, nnnnnnnnn,
oooo, pp, q, rr, s, ttttt,
uuuuu.
Христиан Гюйгенс
(1629-1695)
68.
«Окруженкольцом
«Annulo cingitur
tenui,тонким,
plano,
плоским,
нигде
не
nusquam
cohaerente,
ad
eclipticam
подвешенным, наклонным к
inclinato»
эклиптике»
69.
aaaaaaa, ccccc, d,eeeee, g, h, iiiiiii, lll,
mm, nnnnnnnnn,
oooo, pp, q, rr, s, ttttt,
uuuuu.
Христиан Гюйгенс
(1629-1695)
70.
a7
n
9
c
5
o
4
d
1
p
2
e
5
q
1
g
1
r
2
h
1
s
1
i
7
t
5
l
3
u
5
m
2
всего
61
P (7,5,1,5,1,1,7,3,2,9,4,2,1,2,1,5,5) ?
71.
P (7,5,1,5,1,1,7,3,2,9,4,2,1,2,1,5,5)61!
7! 5! 1 !5! 1! 1! 7! 3! 2! 9! 4! 2! 1! 2! 1! 5! 5!
1060
72. Сочетания с повторениями из n элементов по k
Сочетаниями с повторениями из nэлементов по k называются такие выборки,
которые, имея по k элементов, выбранных
из числа данных n элементов, отличаются
друг от друга только составом элементов
(порядок расположения элементов значения
не имеет), причем один и тот же элемент
может входить в выборку более одного раза.
Харламова Ирина Ю
16.05.16
73. a, b, c
abac
bc
aа
bb
cc
Харламова Ирина Ю
16.05.16
74. Число сочетаний с повторениями из n элементов по k
~kk
Cn Cn k 1
Харламова Ирина Ю
16.05.16
75. Число сочетаний с повторениями из 3 элементов по 2
~22
2
C3 C3 2 1 C4
4!
4!
6
(4 2)! 2! 2! 2!
76. a, b, c
abac
bc
aа
bb
cc
Харламова Ирина Ю
16.05.16
77.
В гастрономеимеются подарочные
коробки конфет четырех
наименований. Сколькими
способами можно заказать набор из 5 коробо
78.
79.
80. Число сочетаний с повторениями из 4 элементов по 5
~55
5
C4 C4 5 1 C8
8!
8!
56
(8 5)! 5! 3! 5!
Харламова Ирина Ю
16.05.16
81.
Что счем
носит
ь
5 7=35
82.
Идеально Нарядно.. Но
А носков
только,
не надо.
пожалуй- Ноги
ста, без потом
помоешь...
носков!
Нет это
не
Рио-деЖанейро
На босу но- Не ой. Но
гу - круче, с в Америке,
носками
(белыми
например,
спортивны- так очень
ми) – гигие- даже ходят
ничнее
Джинсы вещь демократичная. Но не
до такой же
степени
С черными
носками - Тоже
Если
однозначно
носки, то На босу но- подходит.
гу - есть
только
шанс про- (Носкам
белые
бой!).
колоться
Либо на
босу ногу,
либо с
белыми
носками.
На босу
ногу очень
стильно. С
носками очень пожлобски
Лучше,
С голубы- Работает.
если
ми класси- Если так
уж хочется
джинсы
ческими
черные или джинсами - надеть
то,что
темносюда
надо.Носки носки - то
синие, с
или только
модными белые
отворотами на босу
темные.
Мокасины
с костюВ
гробу
Увольне- Слишком
Носки под мы
не
Носки
под
модно. В мом
ние
цвет брюк, видали цвет
носят.
банке тебя Даже
ремень - такое
гарантиро
точно не настоящи
костюма вано
под цвет
поймут
е
сочетани
ботинок
индейцы.
е
Лучше,
если
брюки без
отворотов. Без
носков
актуально,
но не поделовому
Самый
писк.
На босу Особенно
А галстук На босу Ну вы,
если шорты Только на Забудь об
на голую ногу или батенька, ногу,
ниже колена босу ногу этом!
грудь
естествен
и не
повязать? с белыми оригинал! -но
спортивные.
носками
А пятки ухоженные
Полегче на Не
годится,
поворотах.
Классические даже
офисные
ботинки под если
черные брю- шнурки
ки подходят погладит
очень редко
С черными Ни в
носками - городе
всегда
Богдан,
пожалуй- ни в селе
ста
Селифан
Можно
даже в
клуб.
Вместо
носков –
аккуратный
педикюр
С темными носкахороНи в коем ми
шо.
Без
разе
носков еще
лучше
83. Число, положение и комбинация - три взаимно пересекающиеся, но различные сферы мысли, к которым можно отнести все математические идеи.
Число, положениеи комбинация - три
Дж.
Сильвестр
(1844
г.)
взаимно пересекающиеся,
но различные сферы мысли,
к которым можно отнести все


















































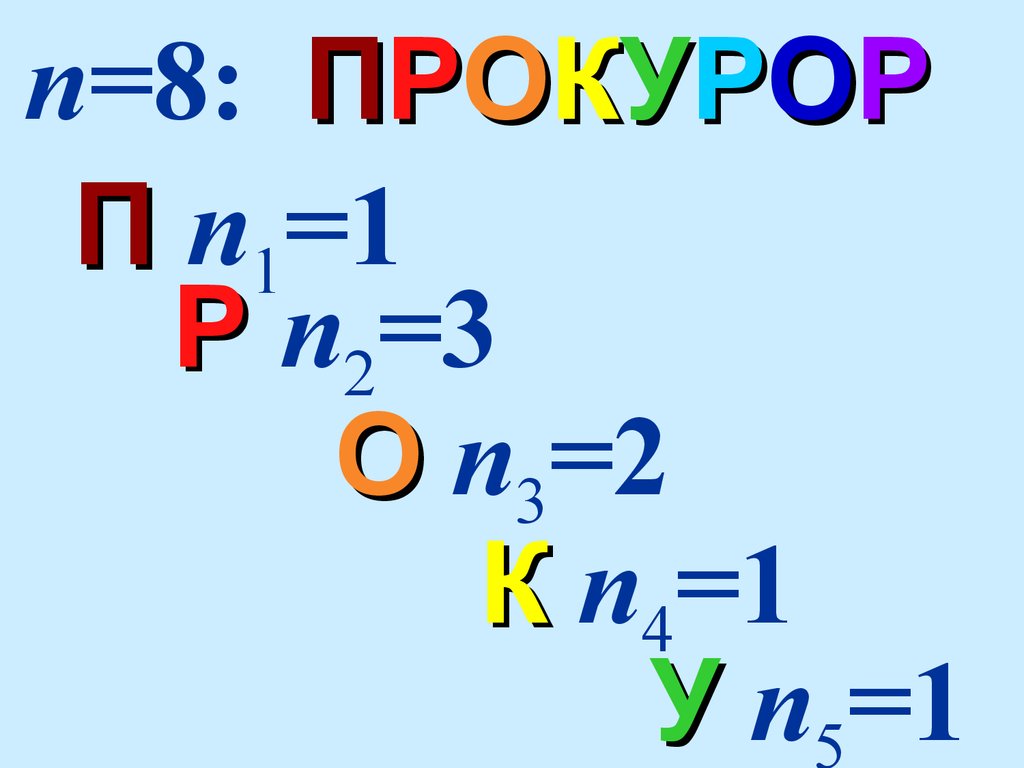
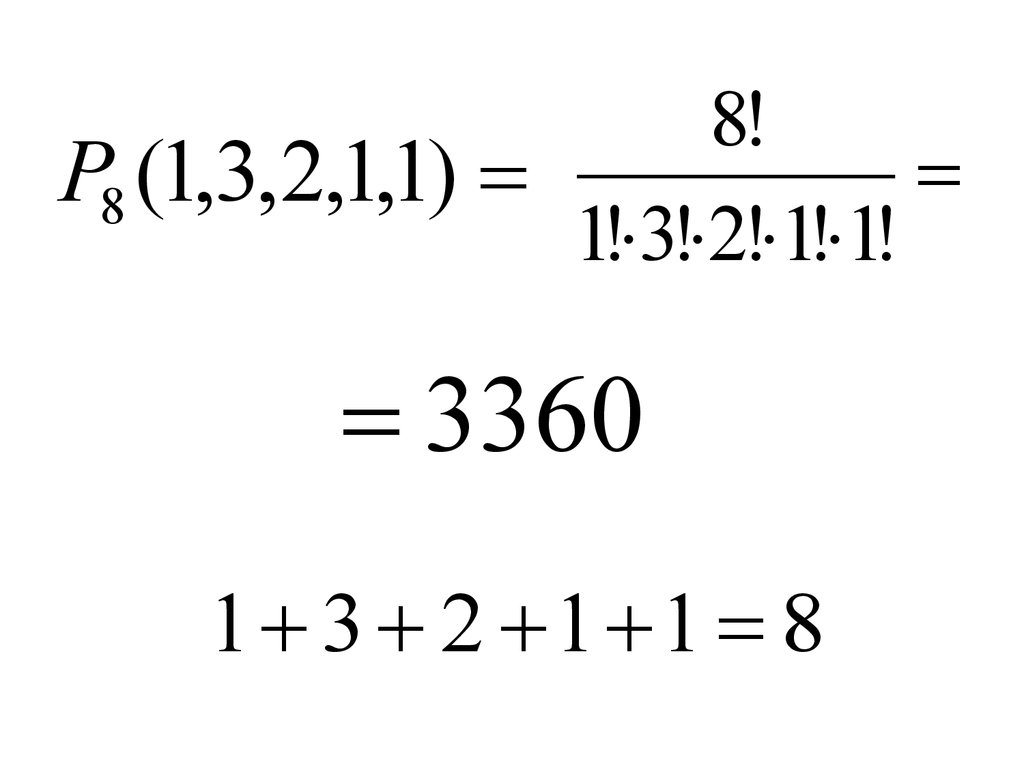
















 Математика
Математика Философия
Философия








