Похожие презентации:
Основы теории вероятностей
1. Основы теории вероятностей
2. Виды событий
ДостоверноеСобытие, которое обязательно произойдёт, если
будет осуществлена определённая совокупность
условий.
Невозможное
Событие, которое заведомо не произойдёт, если
будет осуществлена определённая совокупность
условий.
Случайное
Событие, которое при осуществлении определённой
совокупности условий может либо произойти, либо
не произойти.
3. Предмет теории вероятностей
Предметомтеории
вероятностей является
изучение вероятностных
закономерностей массовых
однородных случайных
событий.
4. Виды случайных событий
НесовместныеОбразующие
полную
группу
Равновозможные
5. Случайное событие
Событие– это результат
испытания.
Элементарный исход –
каждый из возможных
результатов испытания.
Благоприятствующий исход
– тот исход, в котором
интересующее нас событие
произошло.
6. Классическое определение вероятности
Вероятностью события Aназывают отношение числа
благоприятствующих этому
событию исходов к общему
числу всех равновозможных
несовместных элементарных
исходов, образующих полную
группу.
m
P ( A)
n
7. Свойства вероятности
Вероятность достоверногособытия равна единице.
2. Вероятность невозможного
события равна нулю.
3. Вероятность случайного
события есть положительное
число, заключённое между
нулём и единицей.
1.
8. Вывод
Вероятностьлюбого события
удовлетворяет двойному
неравенству:
0 P ( A) 1
9. Пример 1
Изколоды в 36 карт вытащили
одну карту. Какова вероятность,
что это будет бубновая масть?
Решение:
A – из колоды вытащили
бубновую карту
n = 36 (всего 36 карт в колоде)
m = 9 (9 карт бубновой масти)
9 1
P ( A)
0,25
36 4
10. Пример 2
Абонентзабыл две последних цифры
в номере телефона и, помня лишь,
что они различны, набрал их наугад.
Какова вероятность, что набран
правильный номер?
Решение:
A – набран правильный номер
n = 90 (существует всего 90 комбинаций
из двух разных цифр)
m = 1 (только
в одном случае номер
1
P ( A) верным)
0,011
будет
90
11. Комбинаторика
Комбинаторикаизучает
количества комбинаций,
подчинённых определённым
условиям, которые можно
составить из элементов,
безразлично какой природы,
заданного конечного
множества.
12. Перестановки
13. Перестановки
Комбинации, состоящие из однихи тех же n различных элементов и
отличающиеся только порядком
их расположения.
Pn n!
n! 1 2 n
0! 1
14. Пример
Сколькопятизначных чисел
можно составить из цифр 1, 2,
3, 4, 5, если все цифры в числе
разные?
Решение:
n = 5 (имеется 5 разных цифр)
Количество возможных
P5 5! 1 2 3 4 5 120
перестановок:
15. Размещения
16. Размещения
Комбинации, составленные из nразличных элементов по m
элементам, которые отличаются
либо составом элементов, либо их
порядком.
n!
A
(n m)!
m
n
17. Пример
Сколькодвузначных чисел
можно составить из цифр 1, 2, 3,
4, 5, 6, если все цифры в числе
разные?
Решение:
n = 6 (имеется 6 разных цифр)
m = 2 (выбираем по 2 цифры)
Количество возможных
размещений
6!
6! 6 цифр
1 2 3 4по
5 6двум
5 6 30
2
A6 местам:
15
2! (6 2)! 2! 4! 1 2 1 2 3 4 1 2 2
18.
19. Сочетания
Комбинации, составленные из nразличных элементов по m
элементам, которые отличаются
хотя бы одним элементом
(порядок элементов не важен).
n!
C
m! (n m)!
m
n
20. Свойства сочетания
0Cn
1
n
Cn
1
1
Cn
n
n 1
Cn
m
n
n
C C
n m
n
21. Пример
Навитрине магазине 10 видов
пирожных. Сколькими способами
можно выбрать 4 разных
пирожных?
Решение:
n = 10 (имеется 10 разных
пирожных)
m = 4 (выбираем по 4 пирожных)
Количество
возможных
10!
10! 1 2 3 4 комбинаций
5 6 7 8 9 10
4
C10
из 10
4! пирожных
(10 4)! 4! 6! по1 4:
2 3 4 1 2 3 4 5 6
3
7 8 9 10 7 3 10
210
1 2 3 4
1
22. Связь комбинаций
mn
m
n
A C Pm
23. Перестановки с повторениями
Если среди n элементов есть n1элементов одного вида, n2
элементов другого вида и т.д.
(т.е. n = n1 + n2 +…+ nk), то число
перестановок с повторениями
вычисляется по формуле
(n1 n2 ... nk )!
n!
Pn
n1! n2 ! ... nk !
n1! n2 ! ... nk !
24. Размещения с повторениями
Если n различных элементовмогут повториться m раз,
оказавшись соответственно на m
местах, то число размещений с
повторениями вычисляется по
формуле
A n
m
n
m
25. Сочетания с повторениями
Если n различных элементовмогут повториться m раз (без
учёта порядка), то число
сочетаний с повторениями
вычисляется по формуле
(n m 1)!
m
C
Cn m 1
m! (n 1)!
m
n
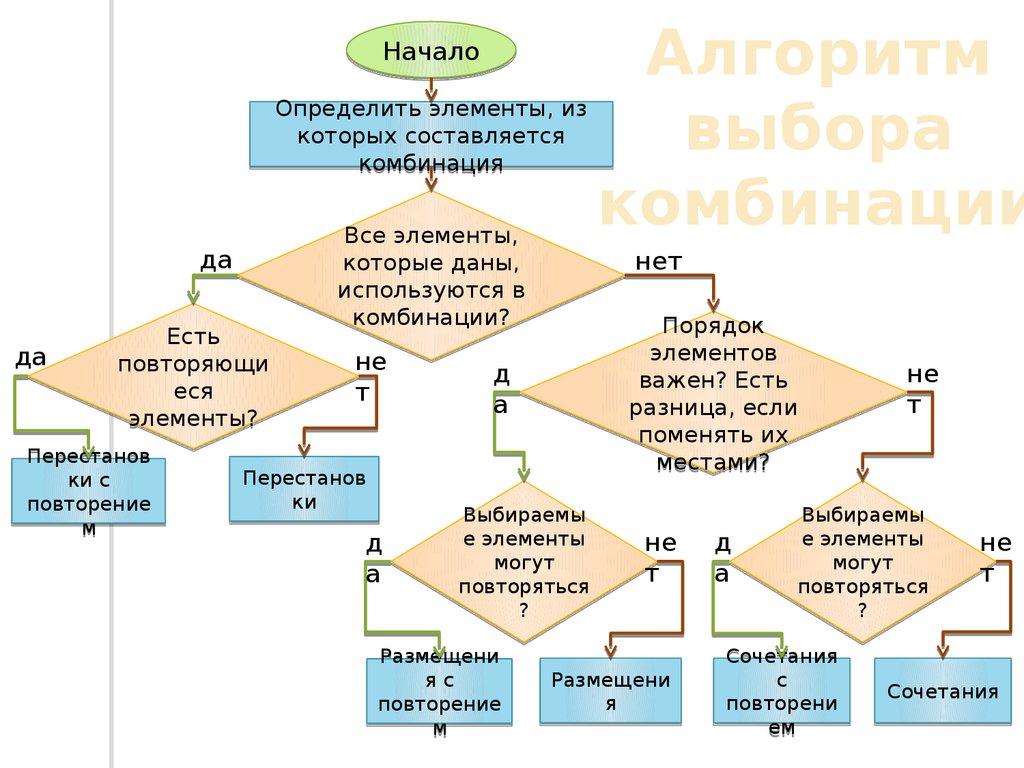
26.
НачалоОпределить элементы, из
которых составляется
комбинация
да
да
Есть
повторяющи
еся
элементы?
Перестанов
ки с
повторение
м
Все элементы,
которые даны,
используются в
комбинации?
не
т
Перестанов
ки
д
а
нет
Порядок
элементов
важен? Есть
разница, если
поменять их
местами?
д
а
Выбираемы
е элементы
могут
повторяться
?
Размещени
яс
повторение
м
Алгоритм
выбора
комбинации
не
т
Размещени
я
д
а
не
т
Выбираемы
е элементы
могут
повторяться
?
Сочетания
с
повторени
ем
не
т
Сочетания
27. Правило суммы
Еслинекоторый объект A
можно выбрать из
совокупности объектов k
способами, а другой объект B
можно выбрать m способами,
то выбрать или A, или B можно
k + m способами.
28. Правило произведения
Еслинекоторый объект A
можно выбрать из
совокупности объектов k
способами, и после каждого
такого выбора другой объект B
можно выбрать m способами,
то выбрать пару объектов A и
B можно k . m способами.




















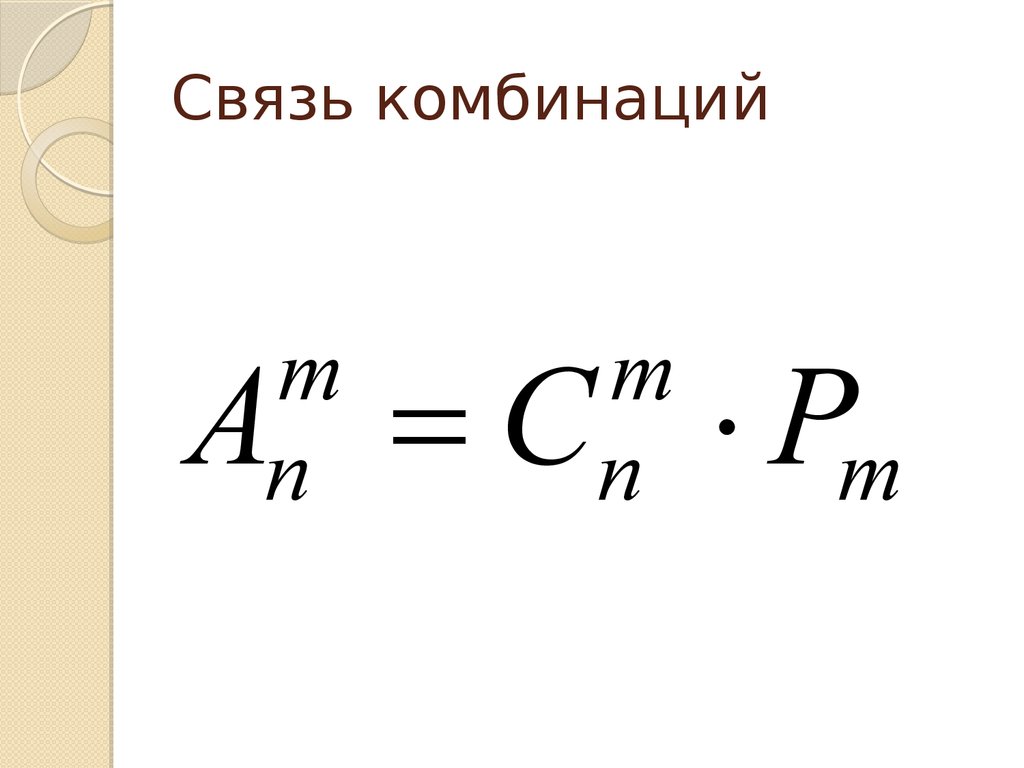






 Математика
Математика








