Похожие презентации:
Кристаллография. Точечные группы симметрии, принцип их вывода с помощью понятия о группах. Формы кристаллов низшей категории
1. КРИСТАЛЛОГРАФИЯ
САНКТ–ПЕТЕРБУРГСКИЙ ГОРНЫЙУНИВЕРСИТЕТ
КРИСТАЛЛОГРАФИЯ
Точечные группы симметрии, принцип их вывода с помощью понятия о группах.
Простые формы кристаллов низшей категории.
лекция № 3
2.
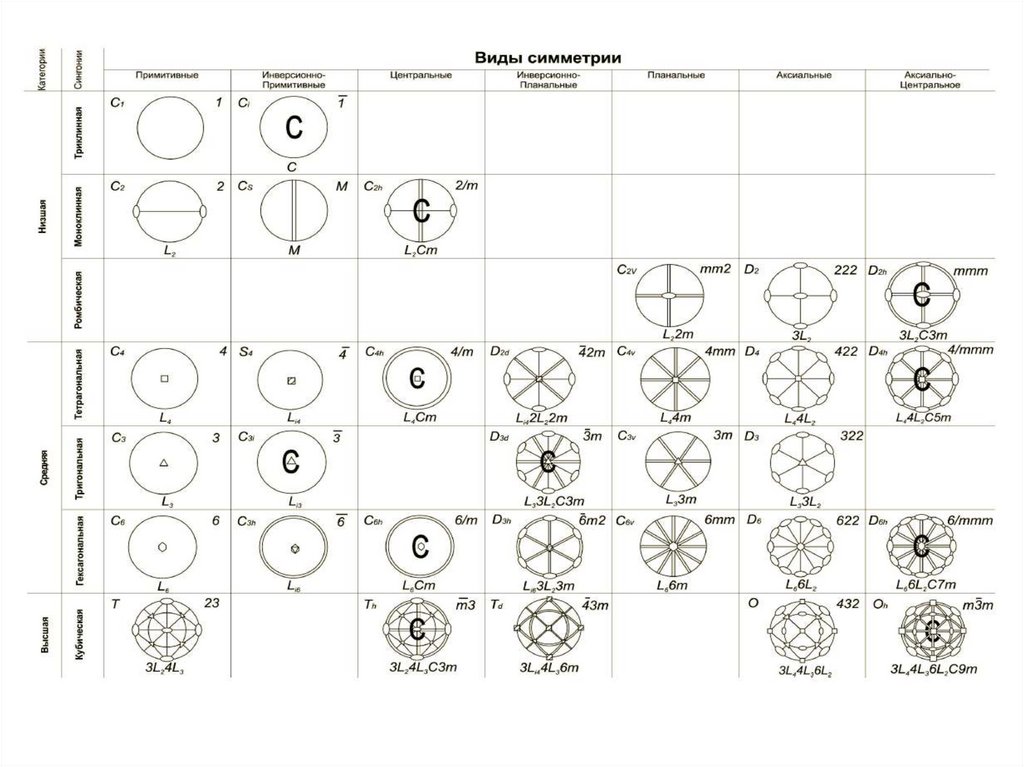
Полная совокупность элементов симметрии кристаллическогомногогранника называется видом симметрий, или точечной группой
симметрии.
Все разнообразие симметрии кристаллических многогранников
исчерпывается 32 видами симметрии
О. Браве
А.В. Гадолин
Е.С. Федоров
3.
4.
5.
6.
7.
8.
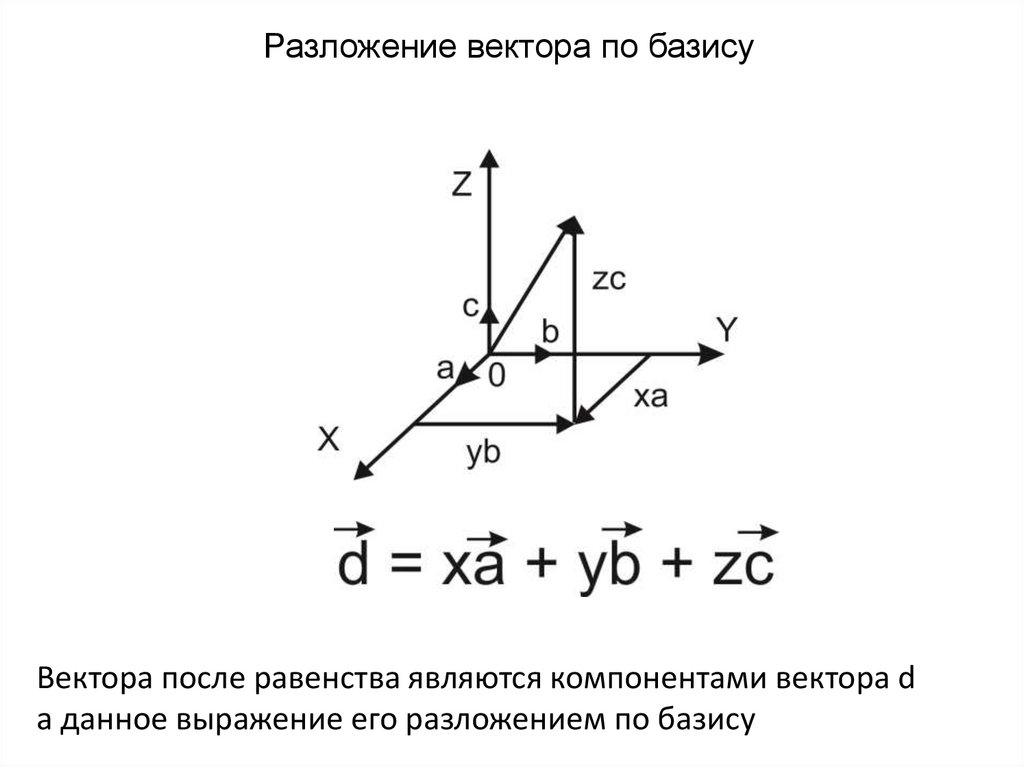
Разложение вектора по базисуВектора после равенства являются компонентами вектора d
а данное выражение его разложением по базису
9.
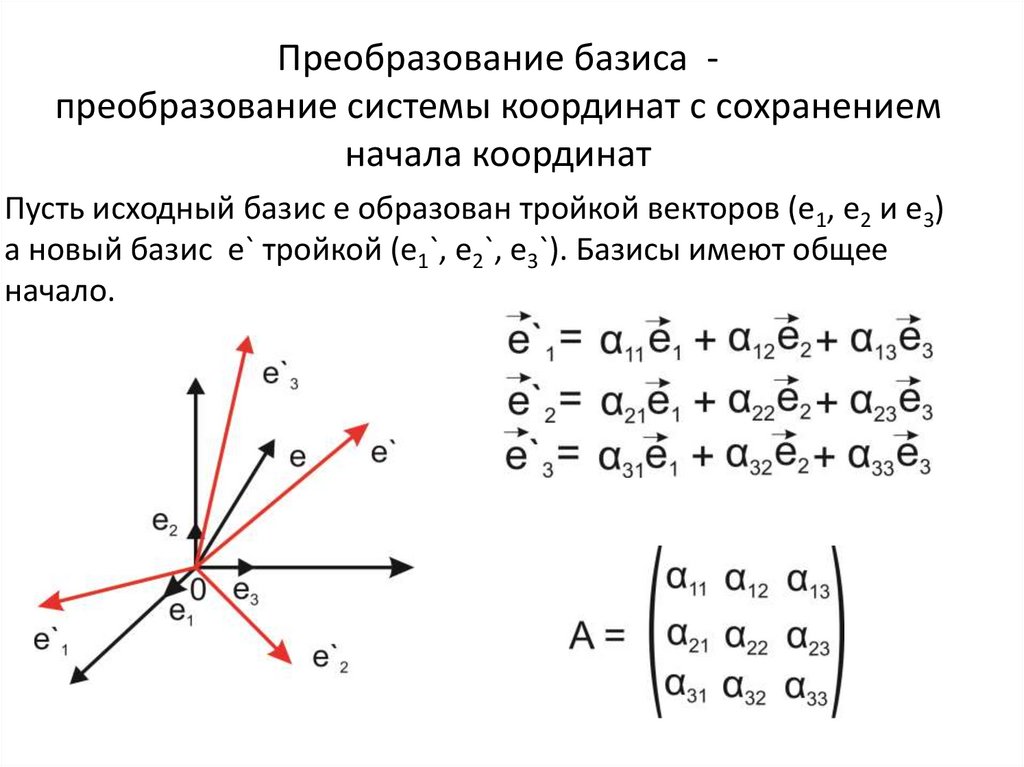
Преобразование базиса преобразование системы координат с сохранениемначала координат
Пусть исходный базис е образован тройкой векторов (е1, е2 и е3)
а новый базис е` тройкой (e1`, e2`, e3`). Базисы имеют общее
начало.
10.
Если фигура составлена из равных частей, равно расположенных друготносительно друга, то существует преобразования, совмещающий равные
части фигуры друг с другом. Такую фигуру называют симметричной,
а преобразования совмещения – преобразованиями или операциями симметрии
преобразования идентичности
поворот вокруг прямой оси
отражение в плоскости
инверсия в точке
поворот вокруг прямой линии с одновременной инверсией в точке
11.
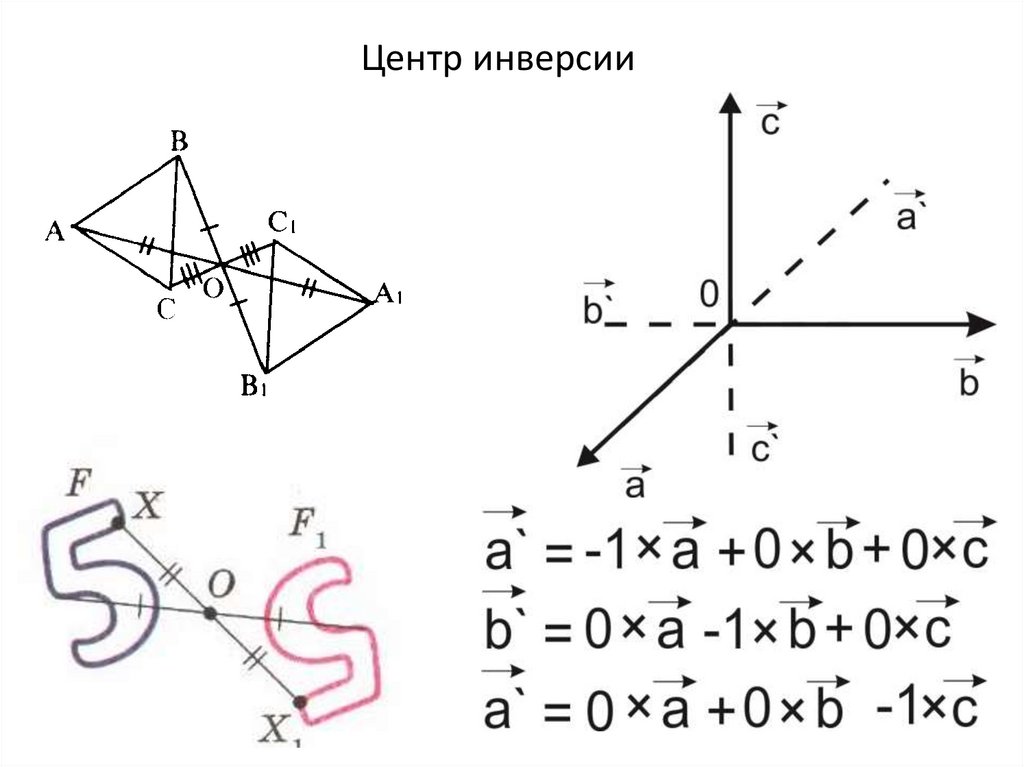
Центр инверсии12.
Центр инверсии13.
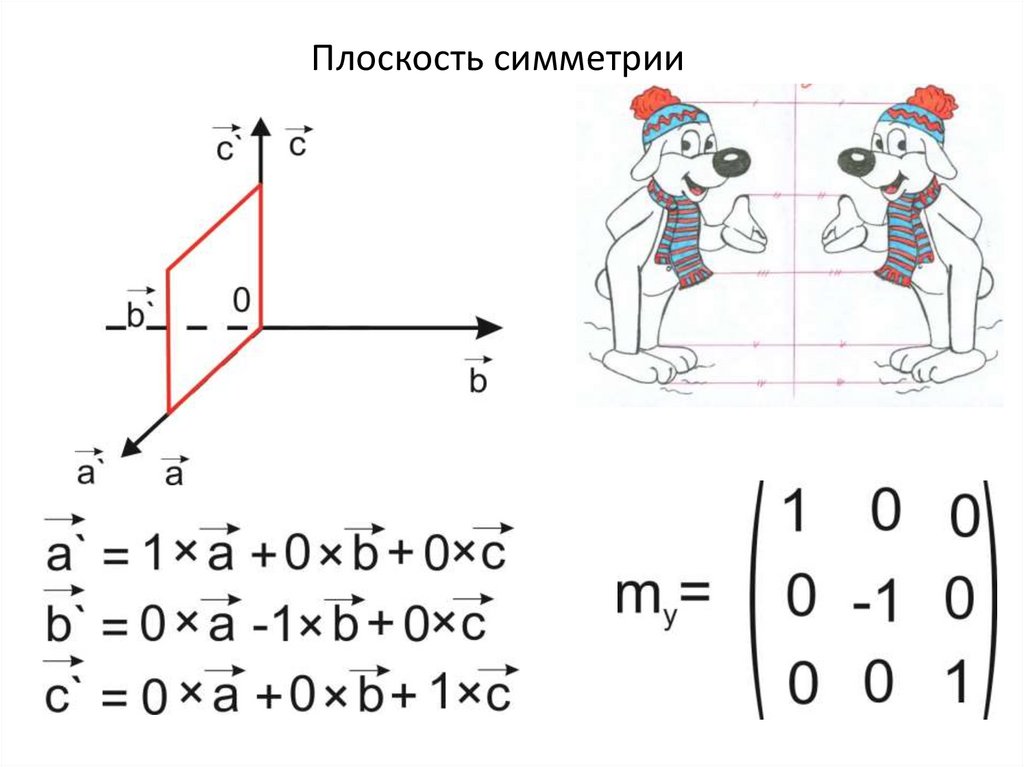
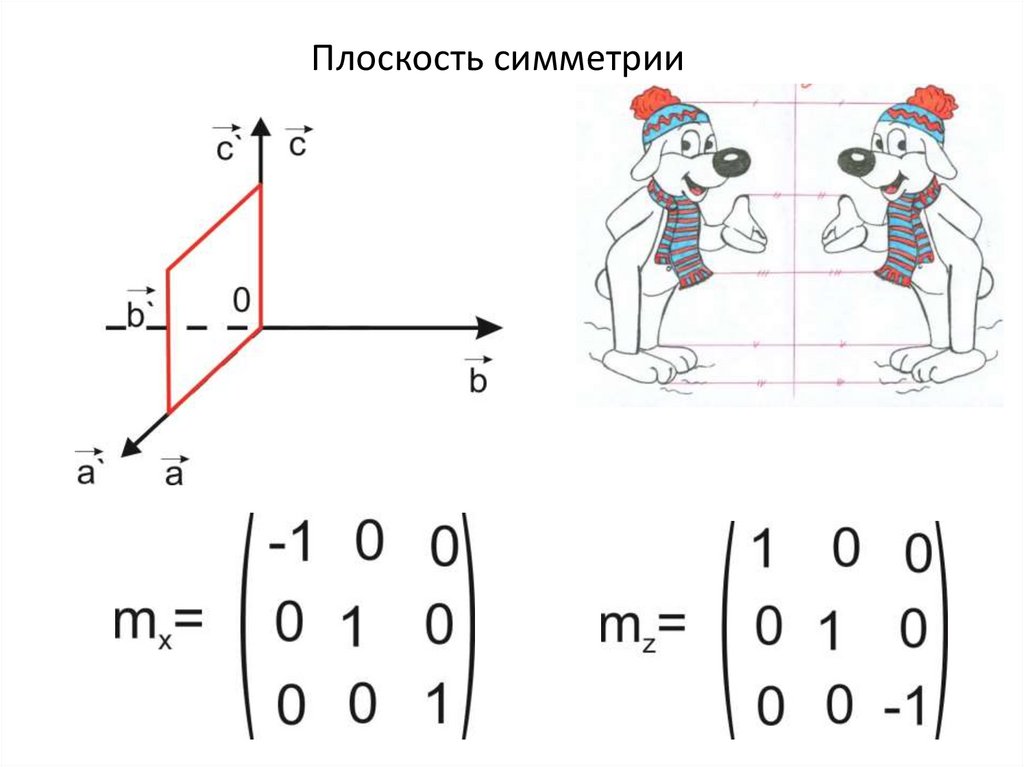
Плоскость симметрии14.
Плоскость симметрии15.
Плоскость симметрии16.
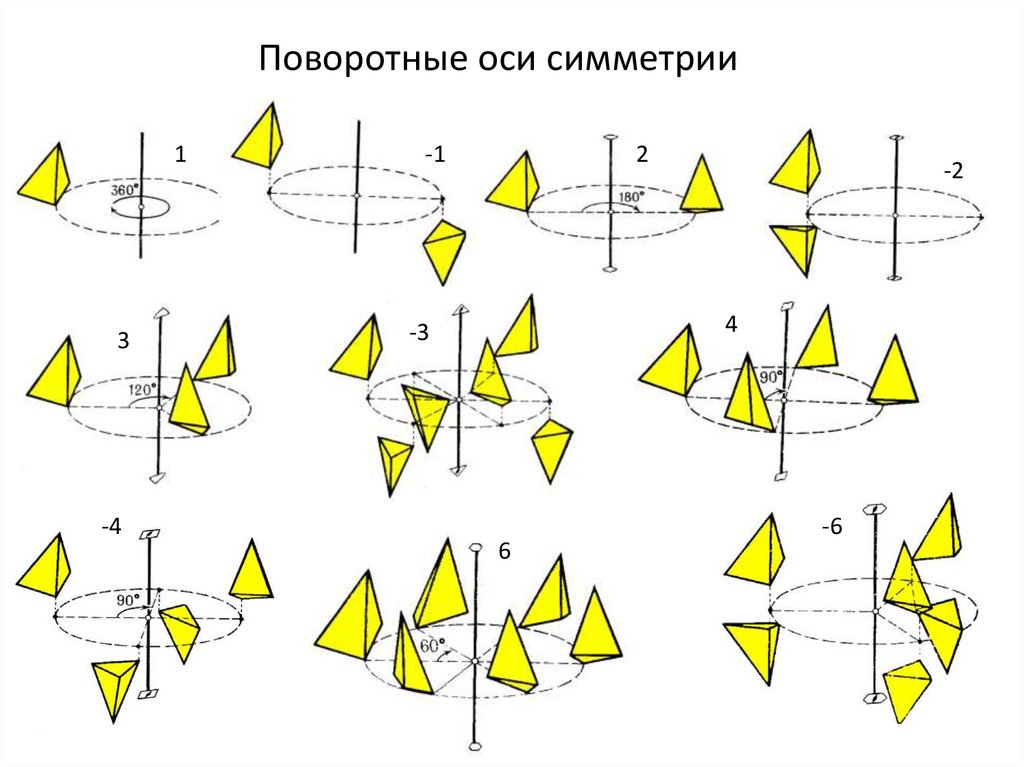
Поворотные оси симметрии1
3
-4
-1
2
-2
4
-3
6
-6
17.
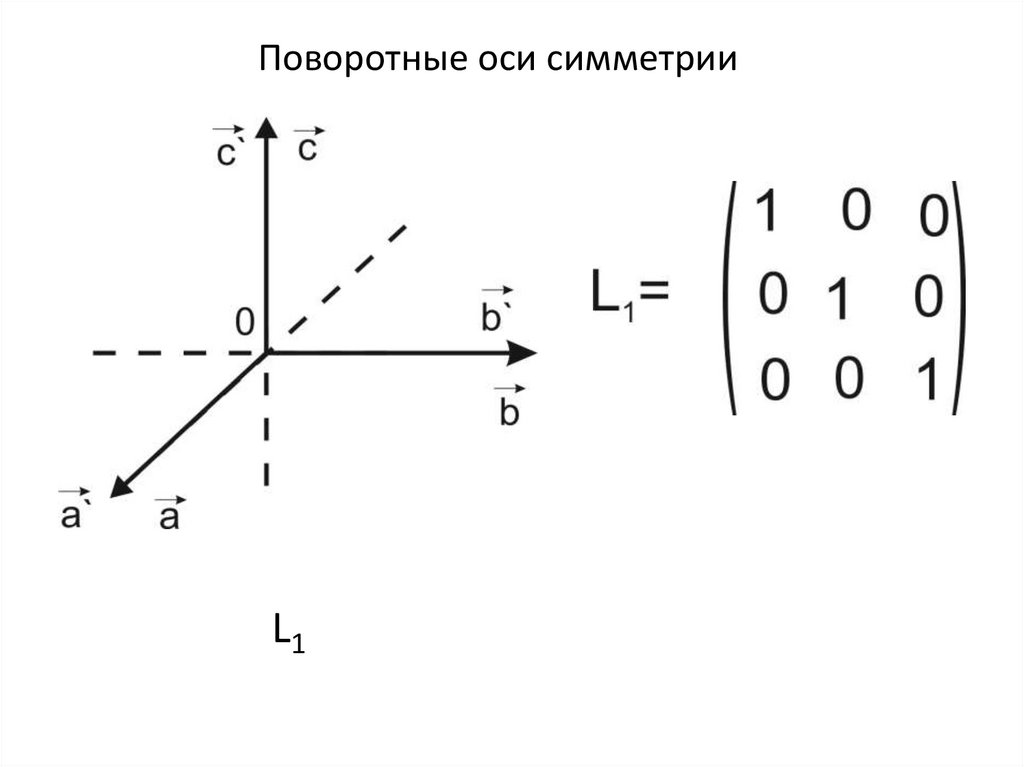
Поворотные оси симметрииL1
18.
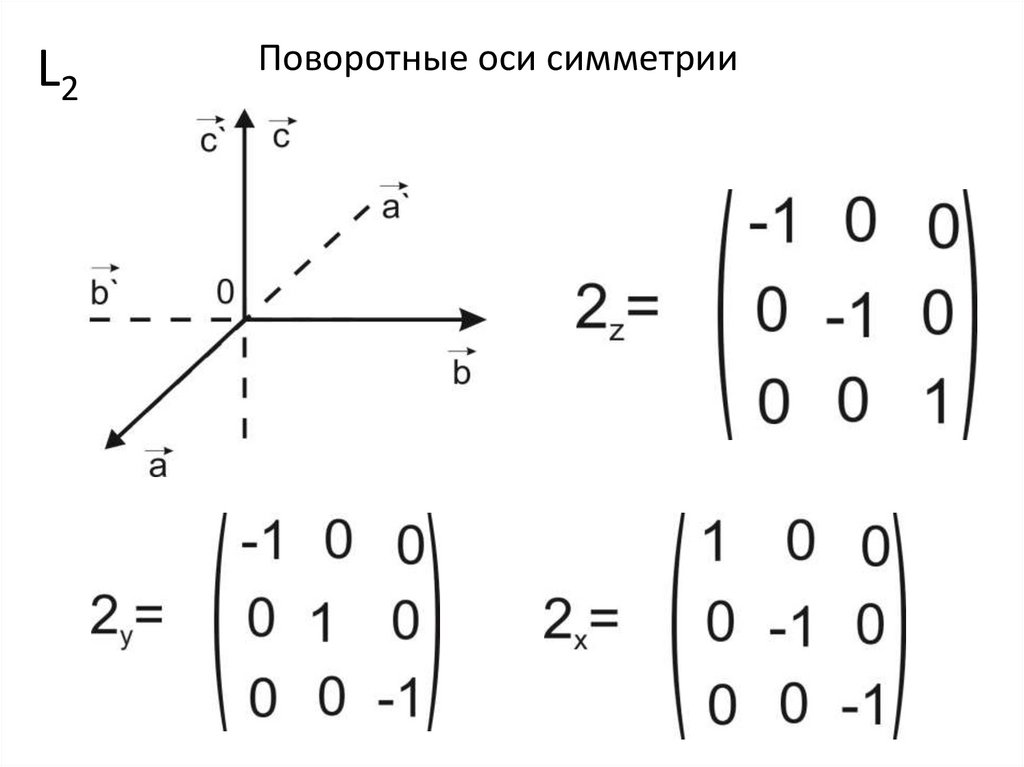
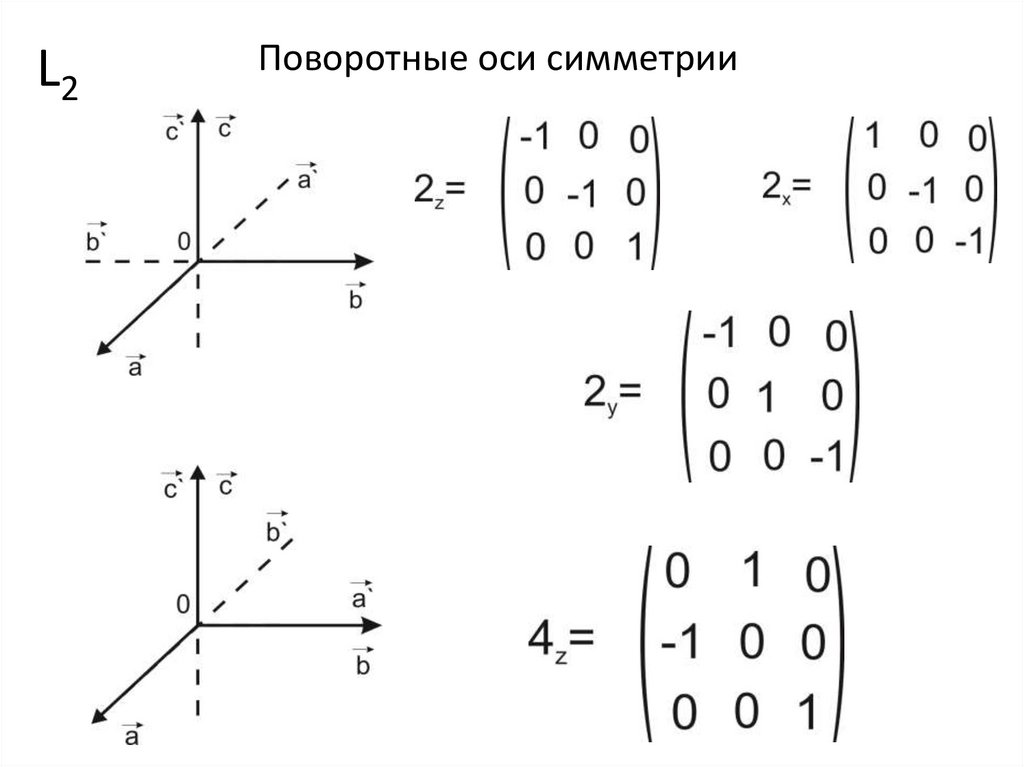
L2Поворотные оси симметрии
19.
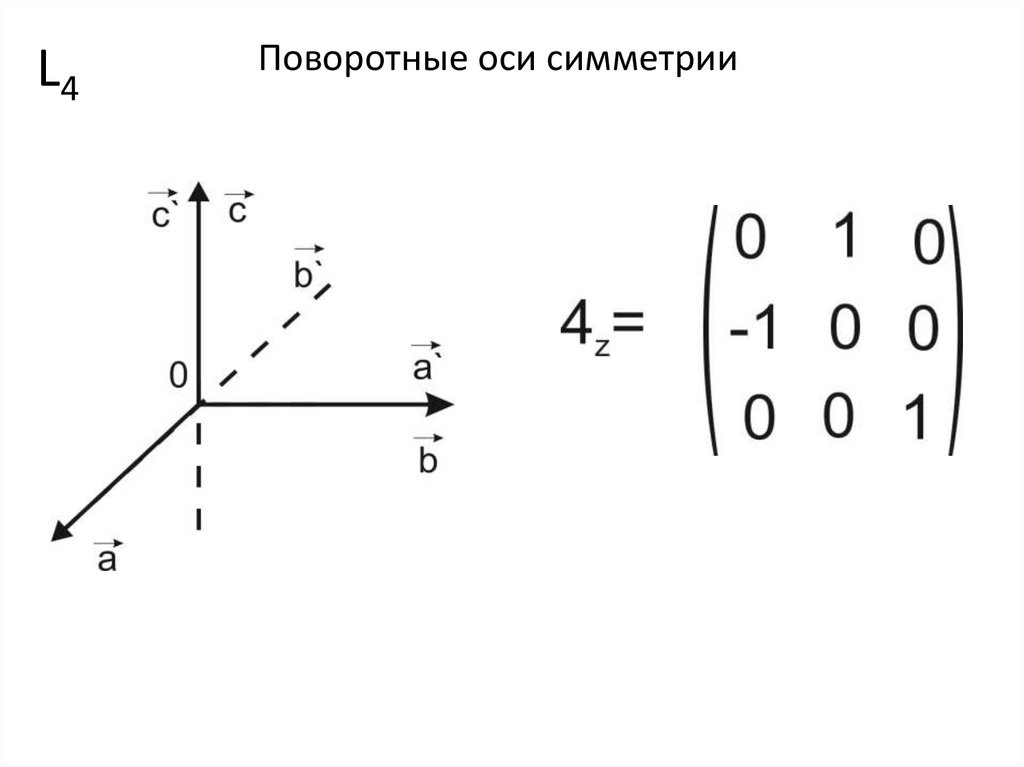
L4Поворотные оси симметрии
20.
L2Поворотные оси симметрии
21.
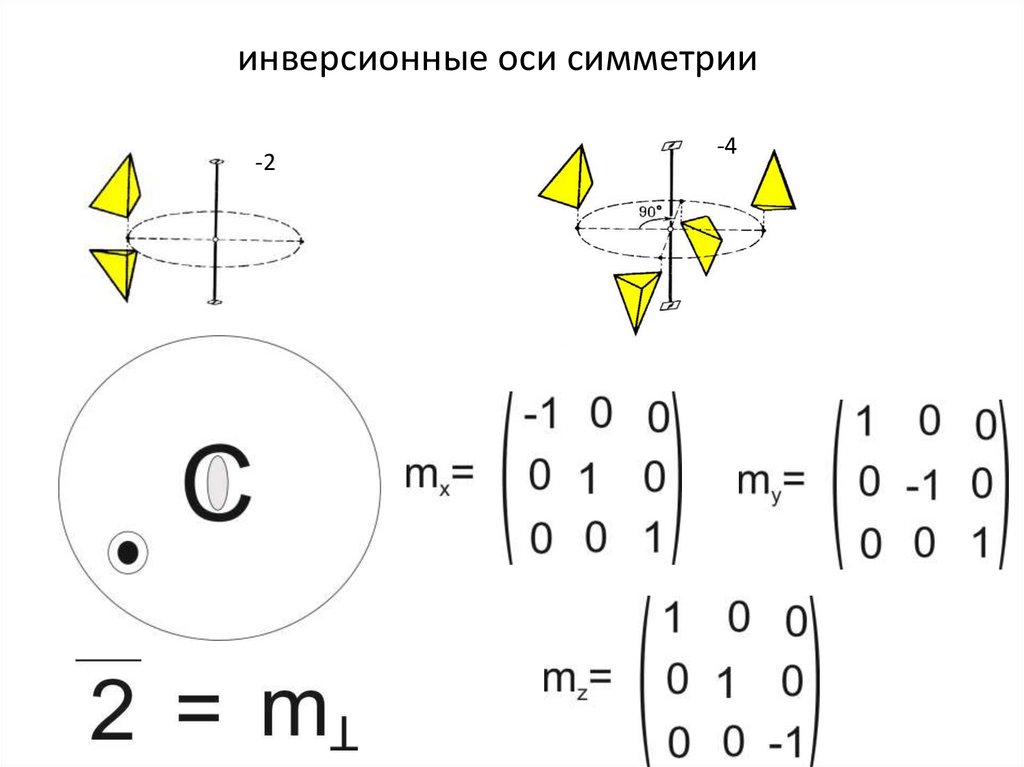
инверсионные оси симметрии-2
-4
22.
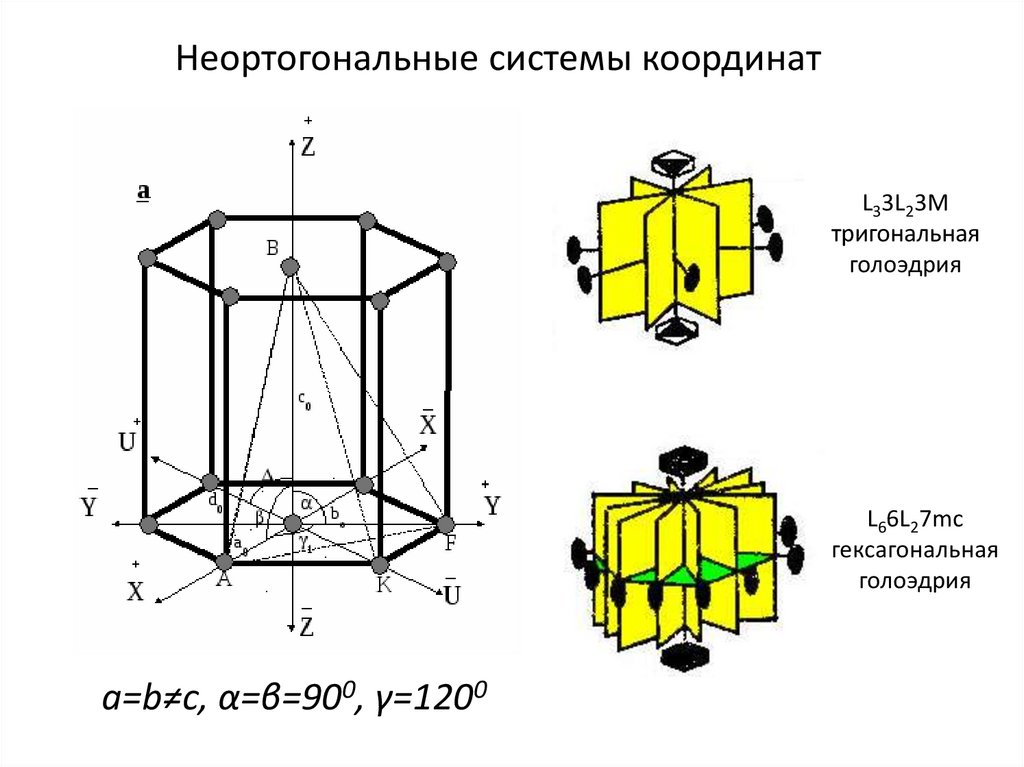
Неортогональные системы координатL33L23M
тригональная
голоэдрия
L66L27mc
гексагональная
голоэдрия
a=b≠c, α=β=900, γ=1200
23.
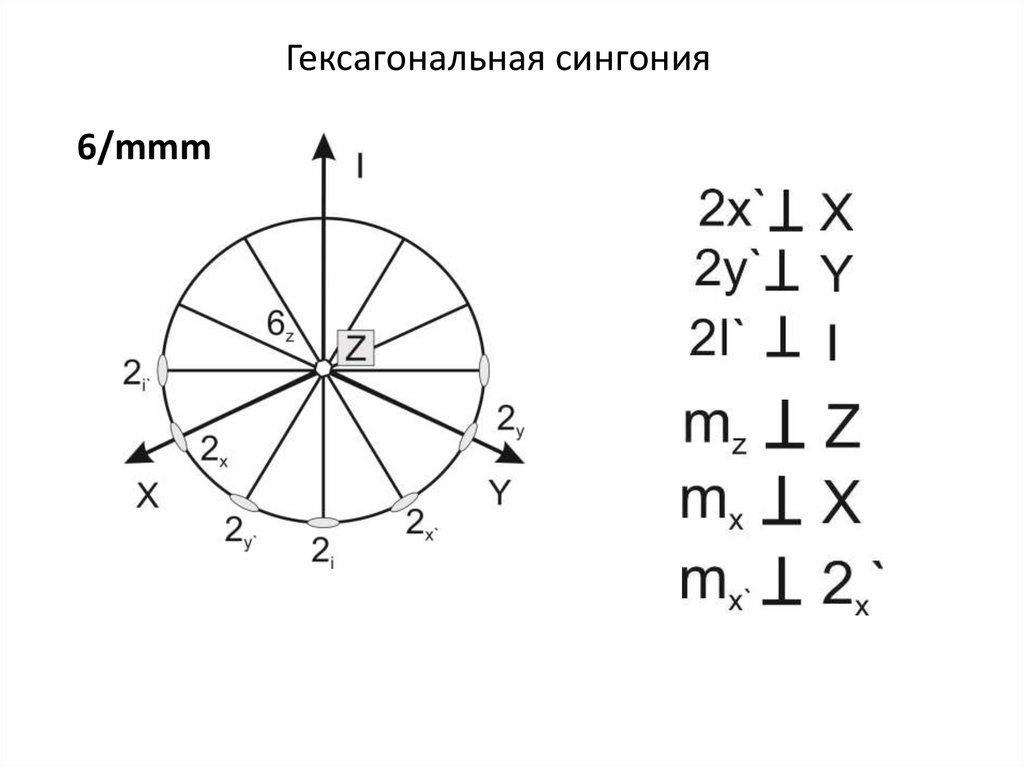
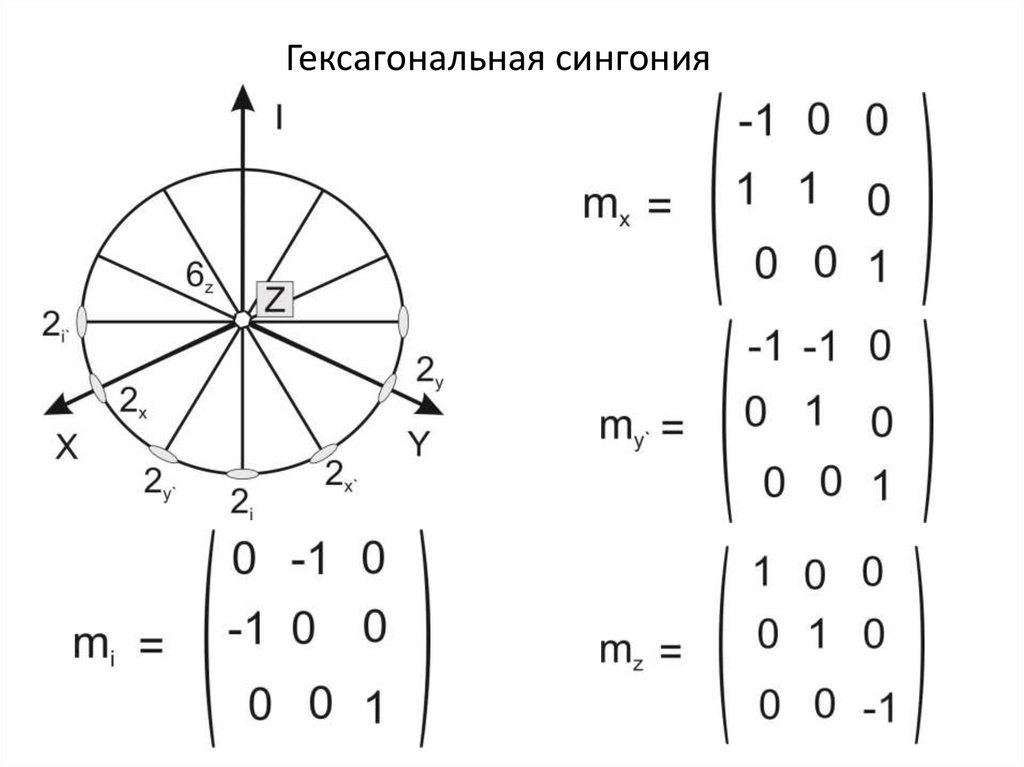
Гексагональная сингония6/mmm
24.
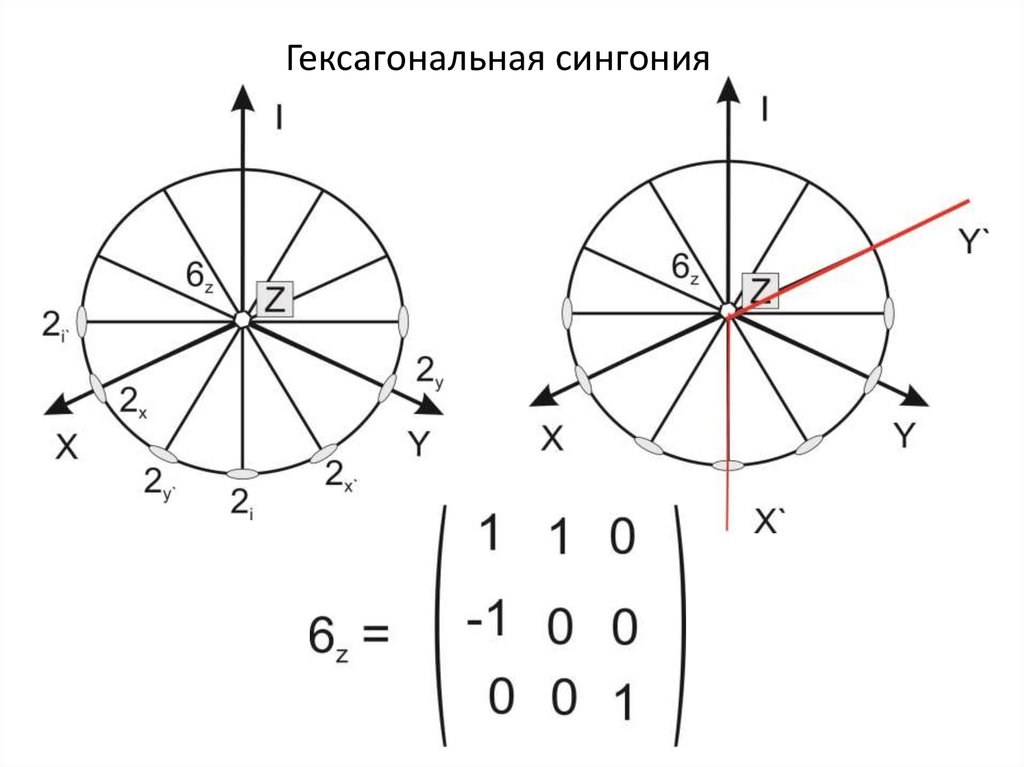
Гексагональная сингония25.
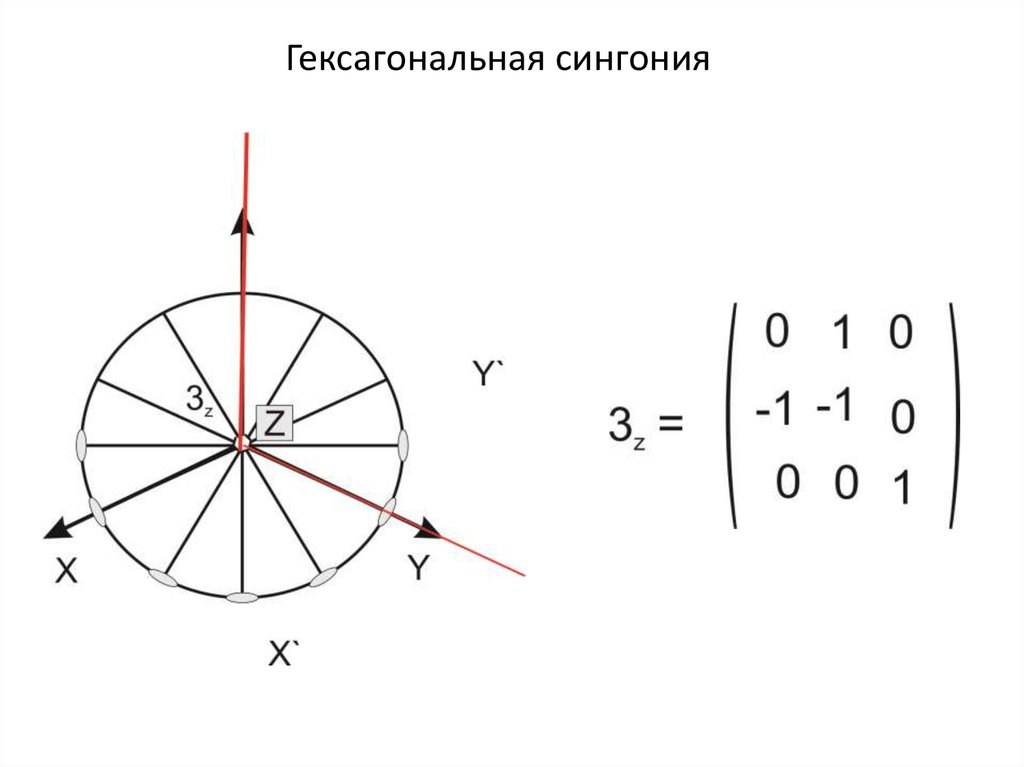
Гексагональная сингония26.
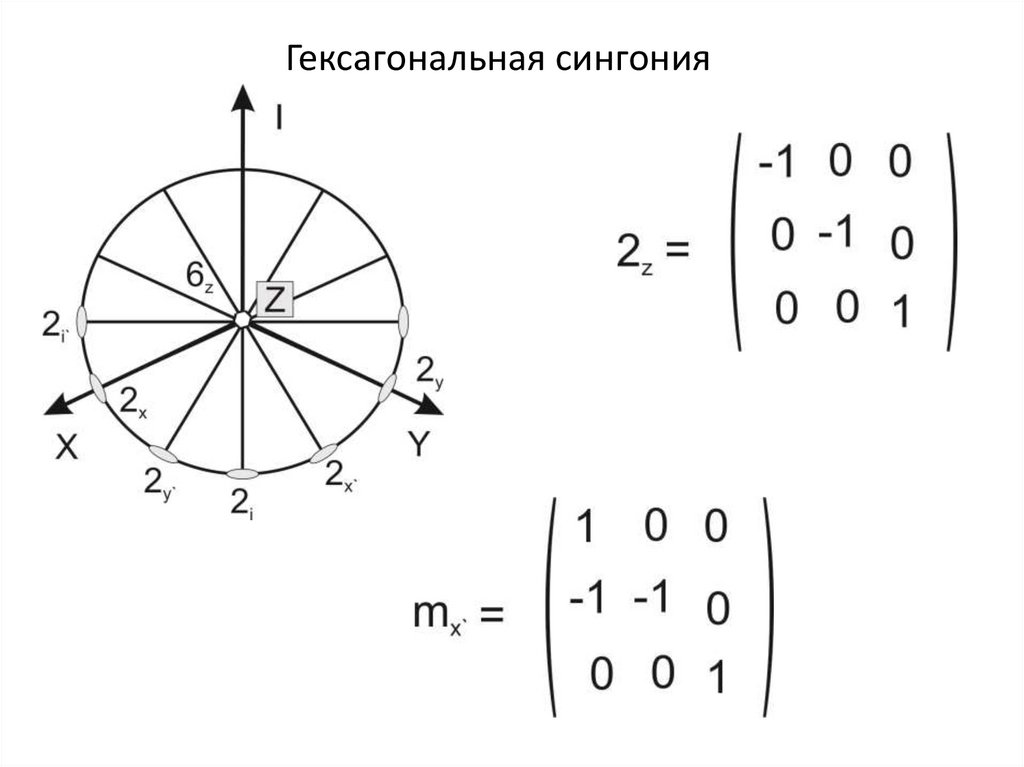
Гексагональная сингония27.
Гексагональная сингония28.
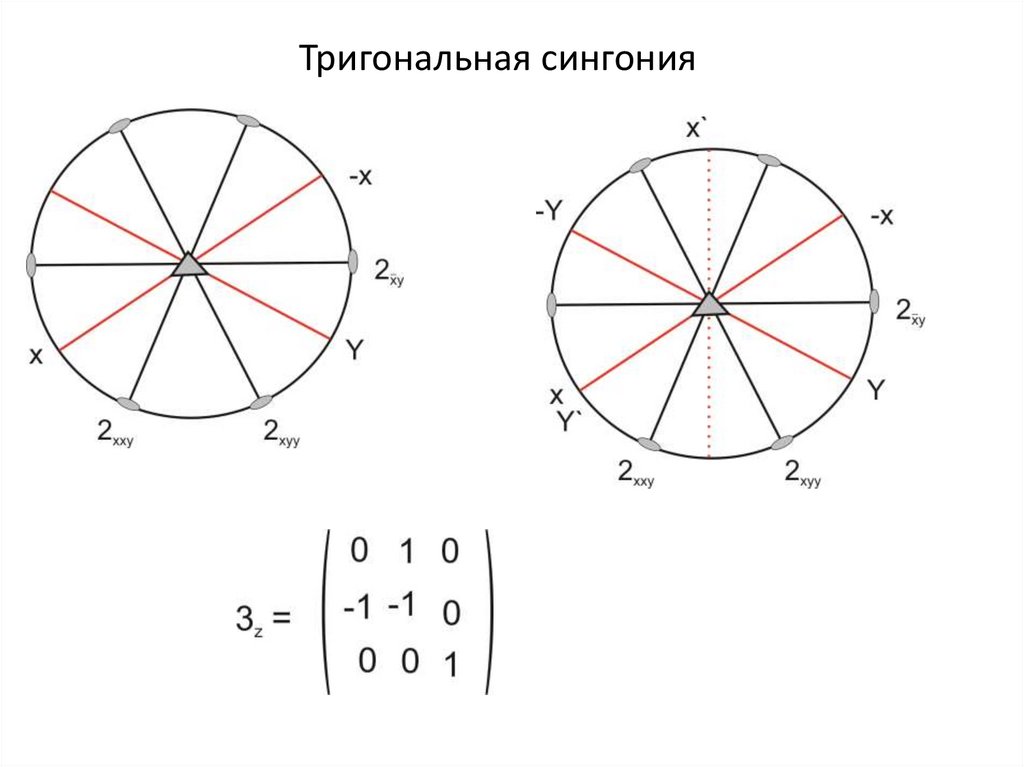
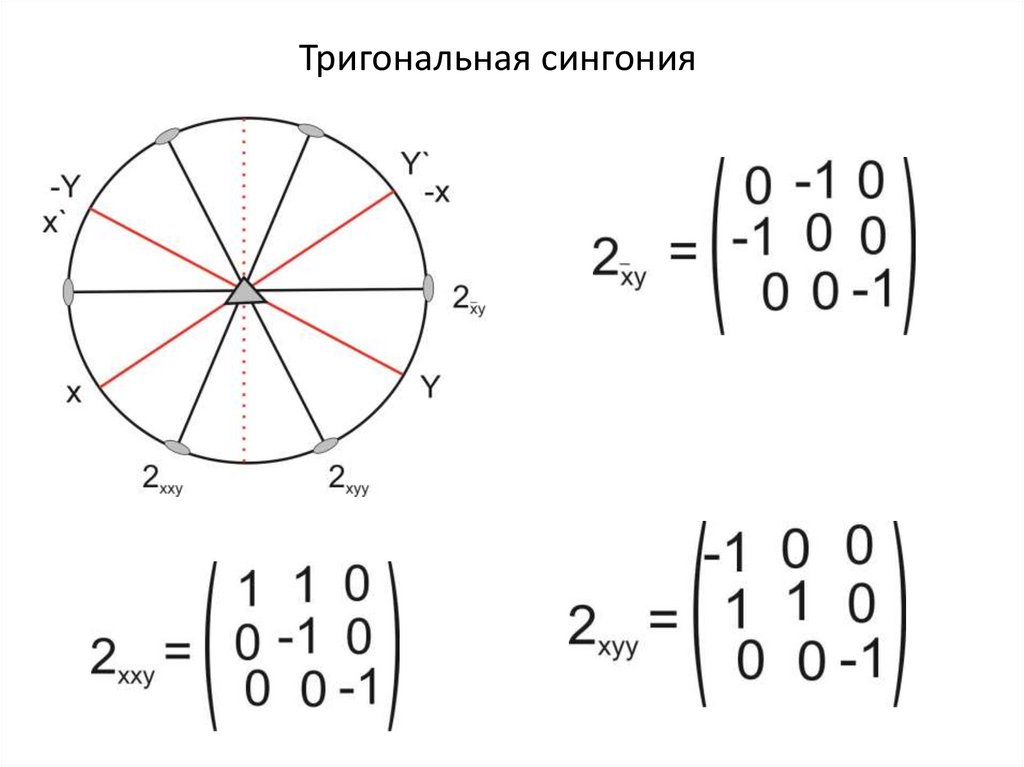
Тригональная сингония29.
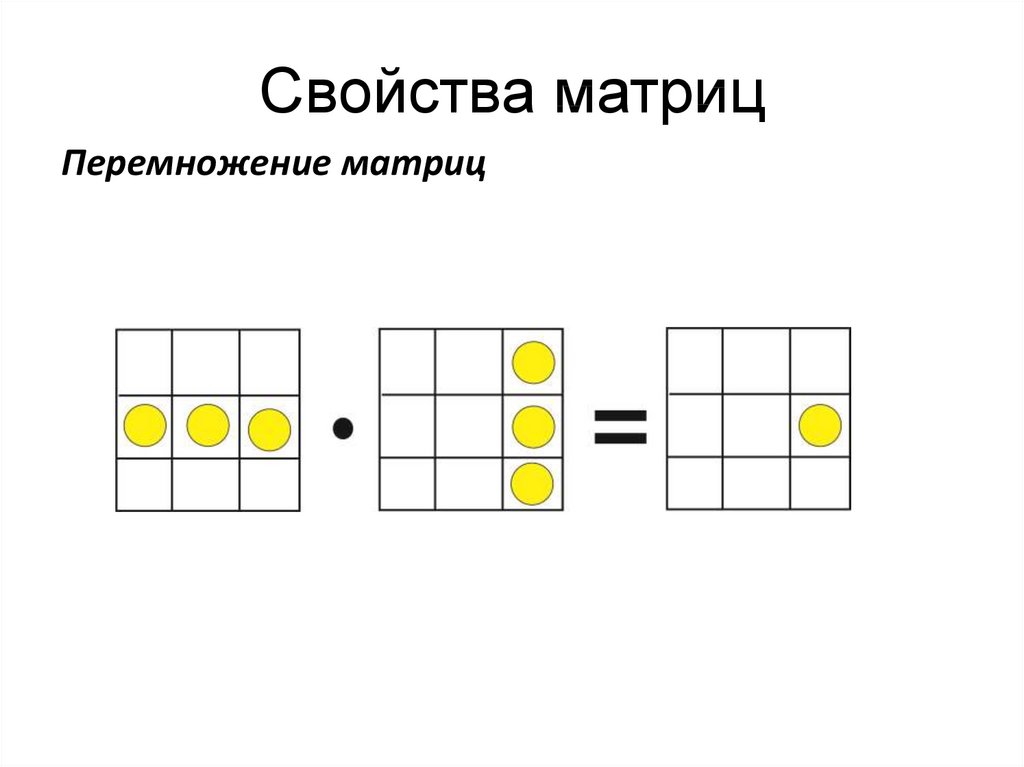
Тригональная сингония30. Свойства матриц
Перемножение матрицПроизведением двух матриц А = αik строения m×n и В = βkj
строения n×r есть матрица С = γijстроения m×r , состоящая
из элементов
31. Свойства матриц
Перемножение матриц32. Свойства матриц
Перемножение матриц33. Умножение матриц
34.
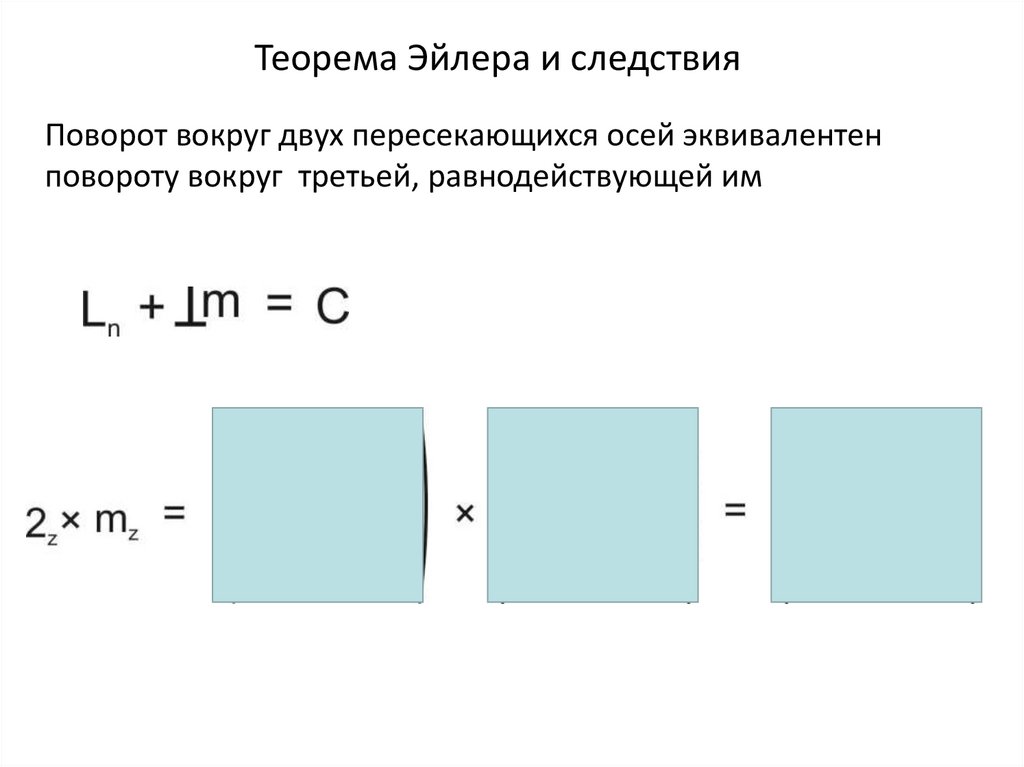
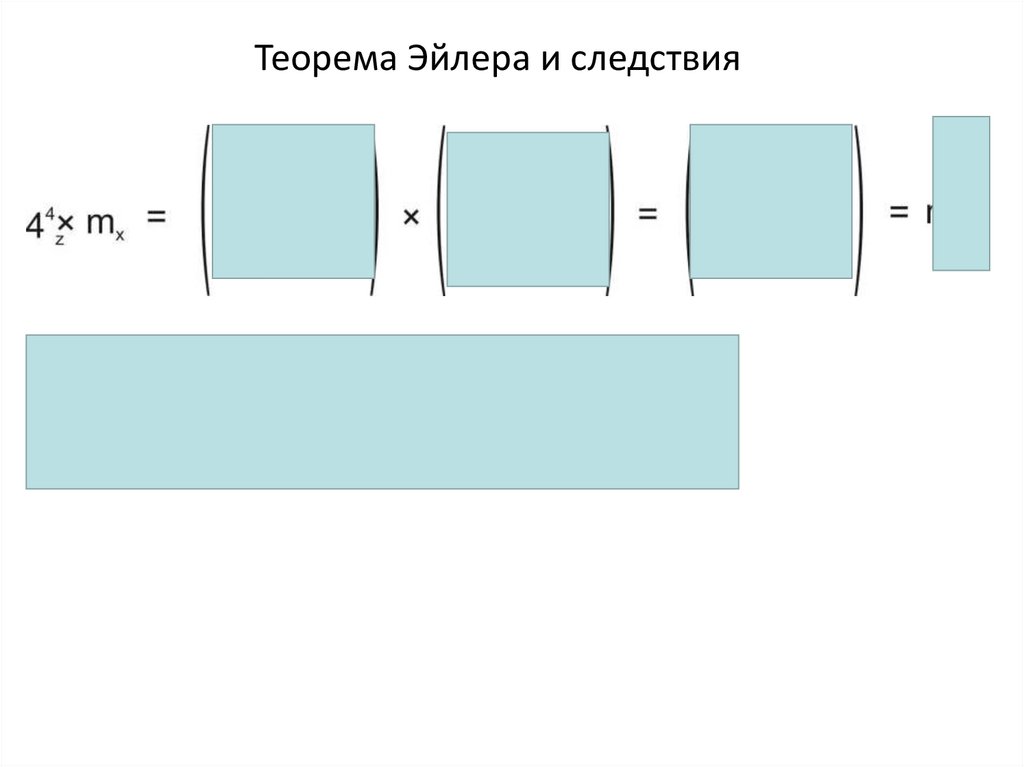
Теорема Эйлера и следствияПоворот вокруг двух пересекающихся осей эквивалентен
повороту вокруг третьей, равнодействующей им
35.
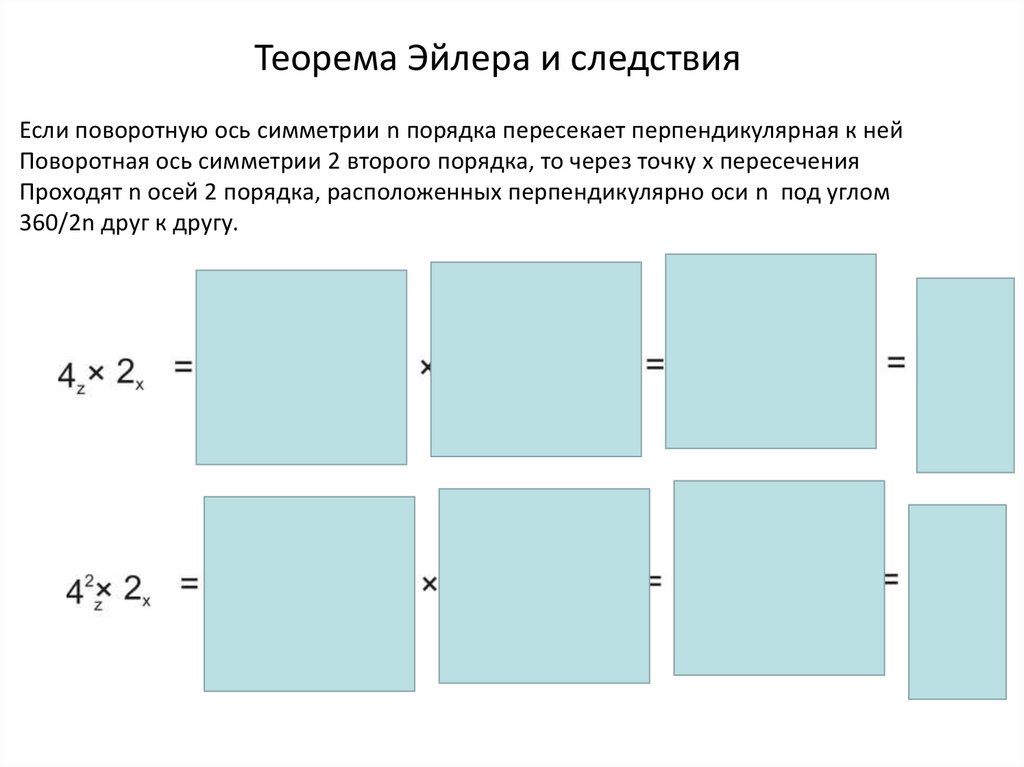
Теорема Эйлера и следствияЕсли поворотную ось симметрии n порядка пересекает перпендикулярная к ней
Поворотная ось симметрии 2 второго порядка, то через точку х пересечения
Проходят n осей 2 порядка, расположенных перпендикулярно оси n под углом
360/2n друг к другу.
36.
Теорема Эйлера и следствия4 оси 2 порядка
под углом
360/8 = 45
37.
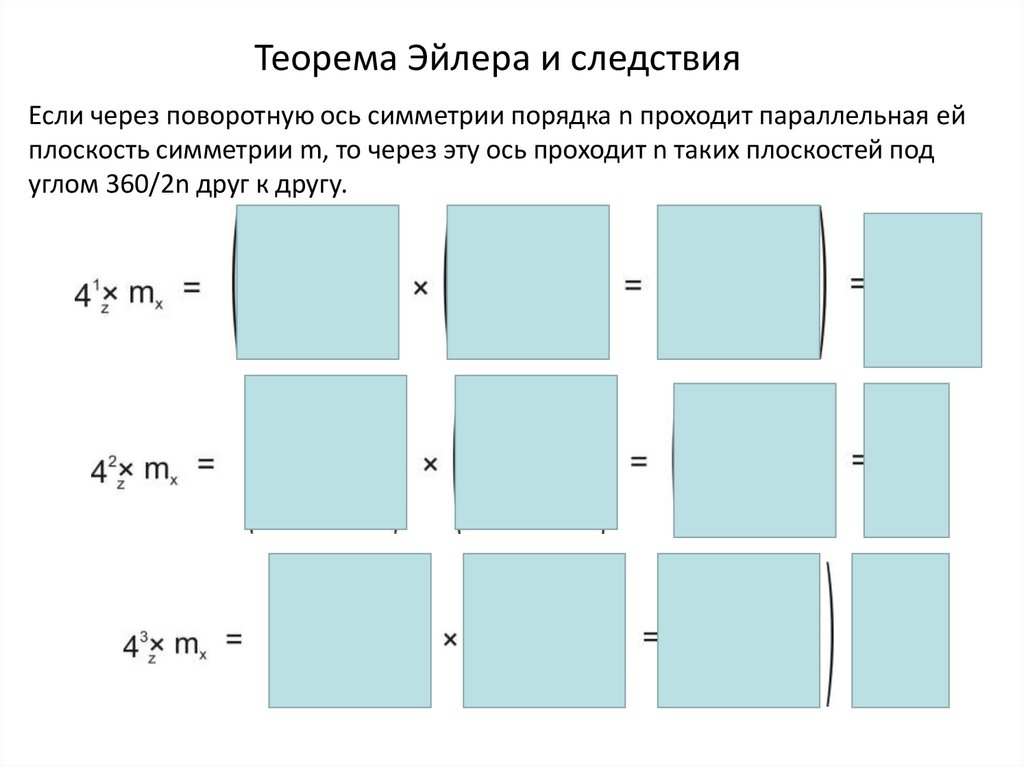
Теорема Эйлера и следствияЕсли через поворотную ось симметрии порядка n проходит параллельная ей
плоскость симметрии m, то через эту ось проходит n таких плоскостей под
углом 360/2n друг к другу.
38.
Теорема Эйлера и следствия4 плоскости m проходящие под 45 градусов
относительно друг друга
39. Группа
Множество G отличных друг от друга элементов называетсягруппой, если выполнены следующие аксиомы:
Существует алгебраическое действие, которое каждой упорядоченной паре элементов
g1 и g2 из G однозначно ставит в соответствие определенный элемент g3=g1g2 из G
Умножение ассоциативно, т.е. для любых трех элементов g1 , g2 и g3 из множества G
справедливо равенство (g1g2)g3=g1(g2g3) = g1g2g3
Существует нейтральный элемент e принадлежащий G такой, что ge = eg = g
для любого g из множества G
Для каждого элемента g принадлежащего G существует обратный
элемент g-1 такой, что gg-1 = g-1g = e
40. Группа
Например:Например: множество целых чисел
Существует алгебраическое действие, которое каждой упорядоченной паре элементов
g1 и g2 из G однозначно ставит в соответствие определенный элемент g3=g1g2 из G
сумма любых двух чисел есть целое число
Умножение ассоциативно, т.е. для любых трех элементов g1 , g2 и g3 из множества G
справедливо равенство (g1g2)g3=g1(g2g3) = g1g2g3
умножение чисел ассоциативно
Существует нейтральный элемент e принадлежащий G такой, что ge = eg = g
для любого g из множества G
нейтральный элемент - 0
Для каждого элемента g принадлежащего G существует обратный
Элемент g-1 такой, что gg-1 = g-1g = e
обратным являются числа с противоположным
знаком ( +1 и -1)
41. Группа
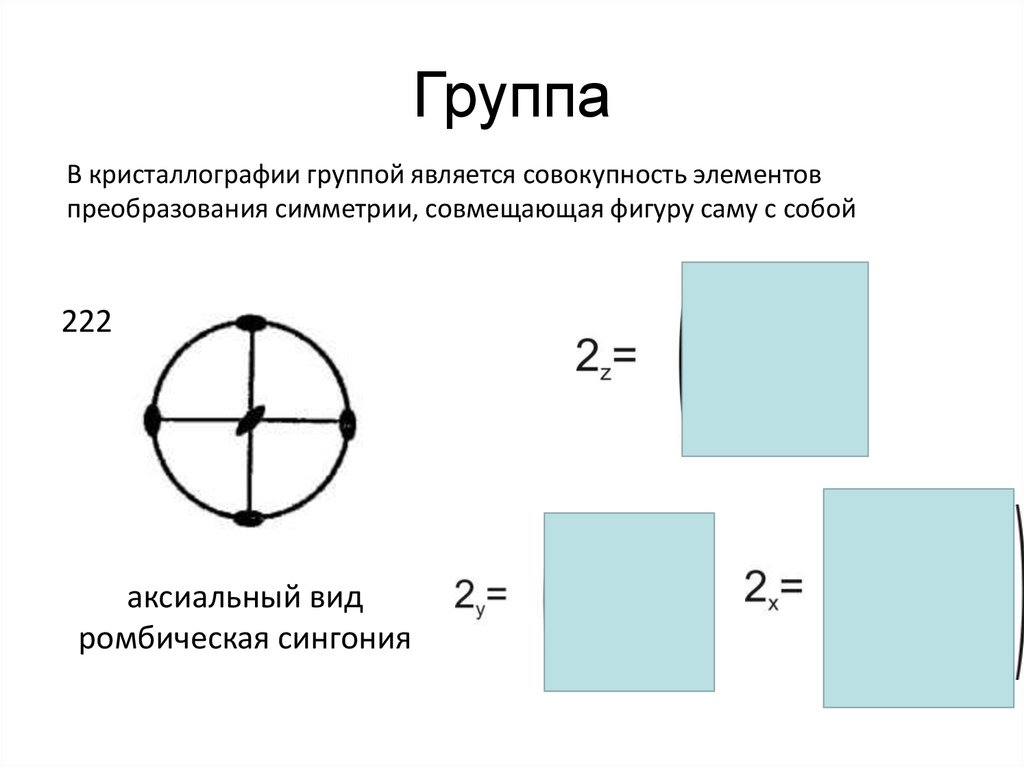
В кристаллографии группой является совокупность элементовпреобразования симметрии, совмещающая фигуру саму с собой
222
аксиальный вид
ромбическая сингония
42. Группа
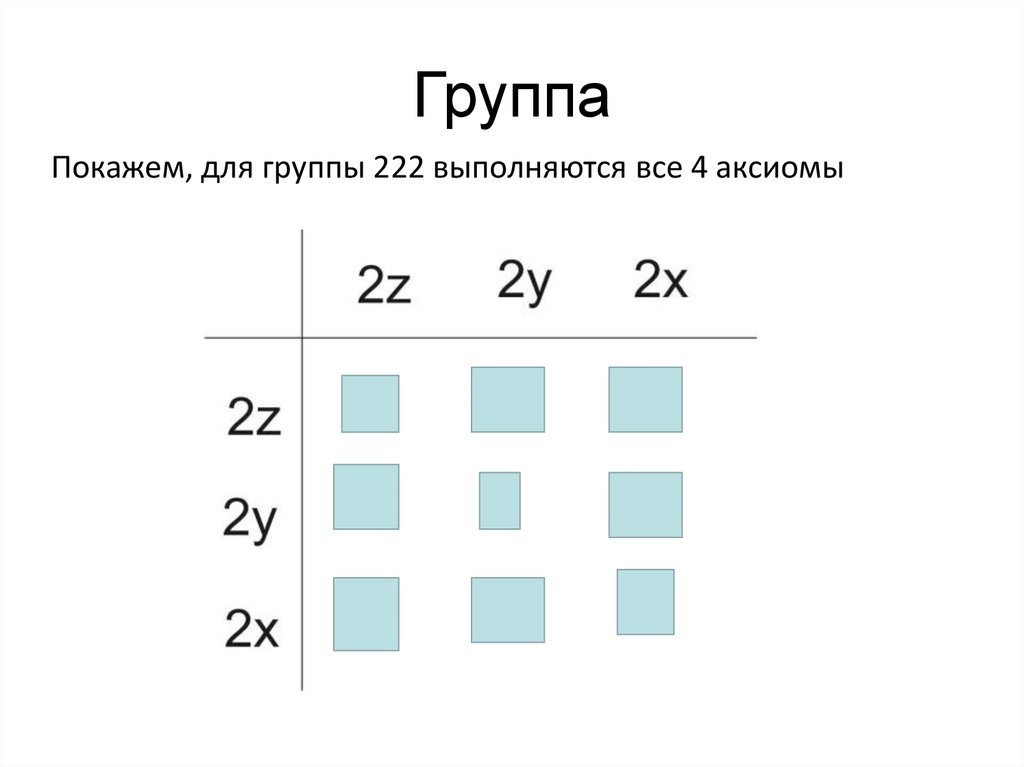
Покажем, для группы 222 выполняются все 4 аксиомы43.
Такая запись получиланазвание квадрат Кейли
Существует алгебраическое действие, которое каждой упорядоченной паре элементов
g1 и g2 из G однозначно ставит в соответствие определенный элемент g3=g1g2 из G
Умножение всех элементов друг на друга не дало новых
элементов симметрии, следовательно множество замкнуто
относительно умножения
44.
Умножение ассоциативно, т.е. для любых трех элементов g1 , g2 и g3 из множества Gсправедливо равенство (g1g2)g3=g1(g2g3) = g1g2g3
Умножение матриц, элементами которых являются числа
ассоциативно по определению
Существует нейтральный элемент e принадлежащий G такой, что ge = eg = g
для любого g из множества G
Нейтральным элементом является единичная матрица
Для каждого элемента g принадлежащего G существует обратный
Элемент g-1 такой, что gg-1 = g-1g = e
Каждый элемент группы является обратным
2z ×2z = 1
Таким образом группа 222 полностью удовлетворяет все
аксиомам
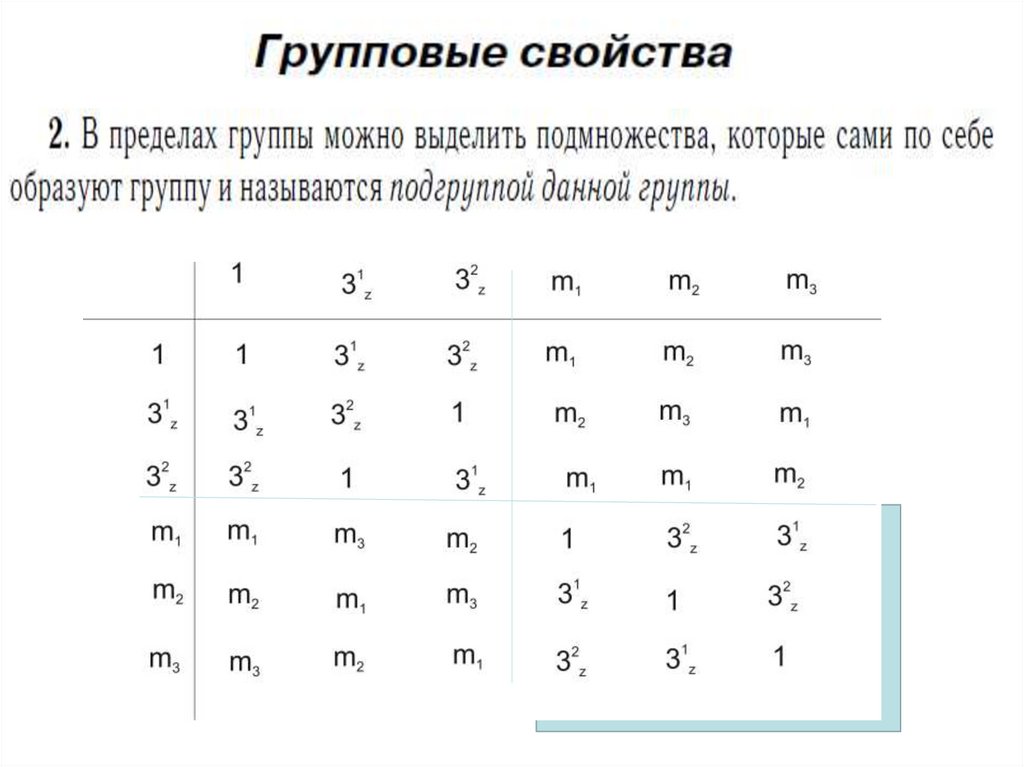
45.
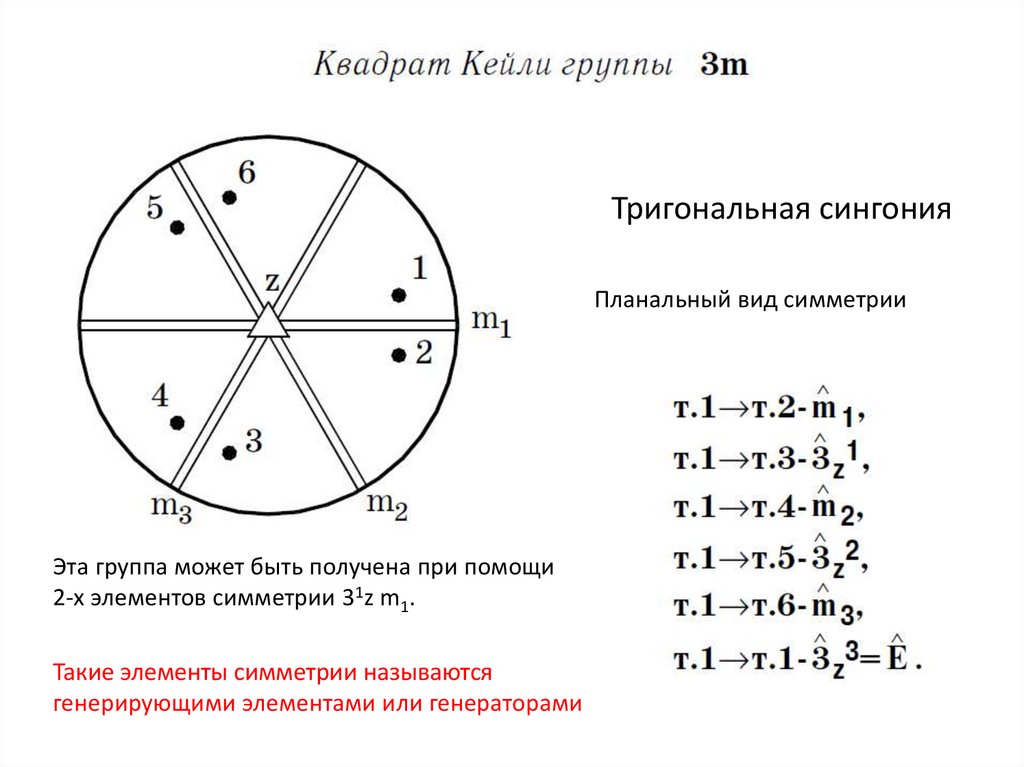
Тригональная сингонияПланальный вид симметрии
Эта группа может быть получена при помощи
2-х элементов симметрии 31z m1.
Такие элементы симметрии называются
генерирующими элементами или генераторами
46.
47.
Доказать все аксиомы без квадрата Кейли48.
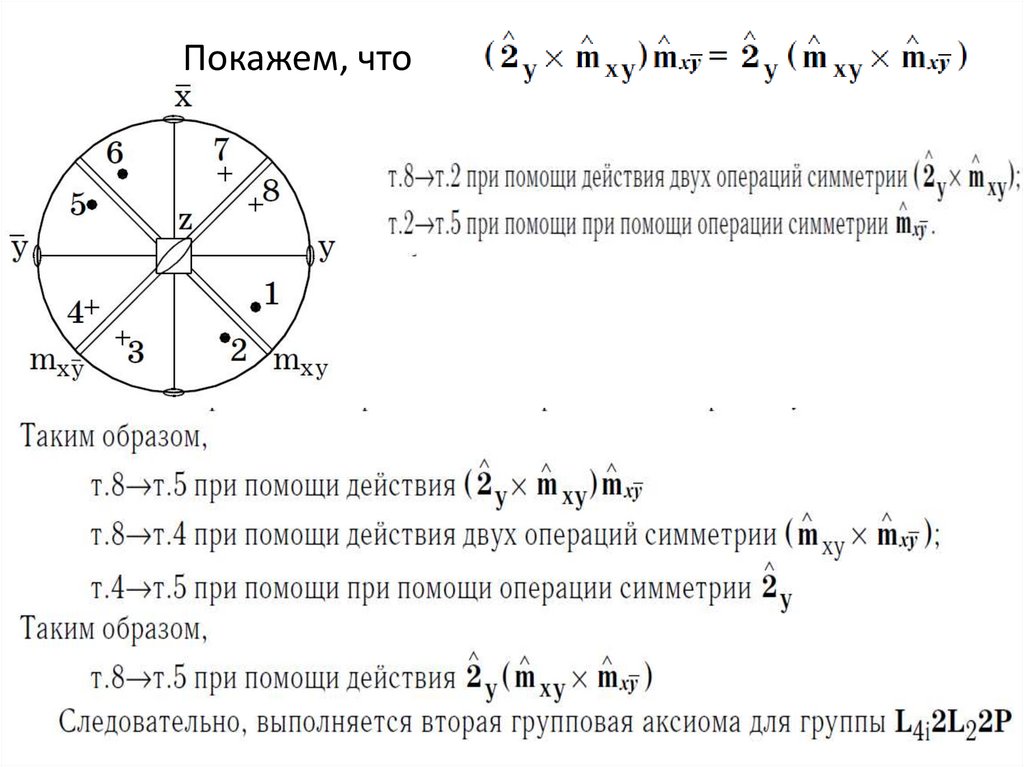
Покажем, что49.
Покажем, что50.
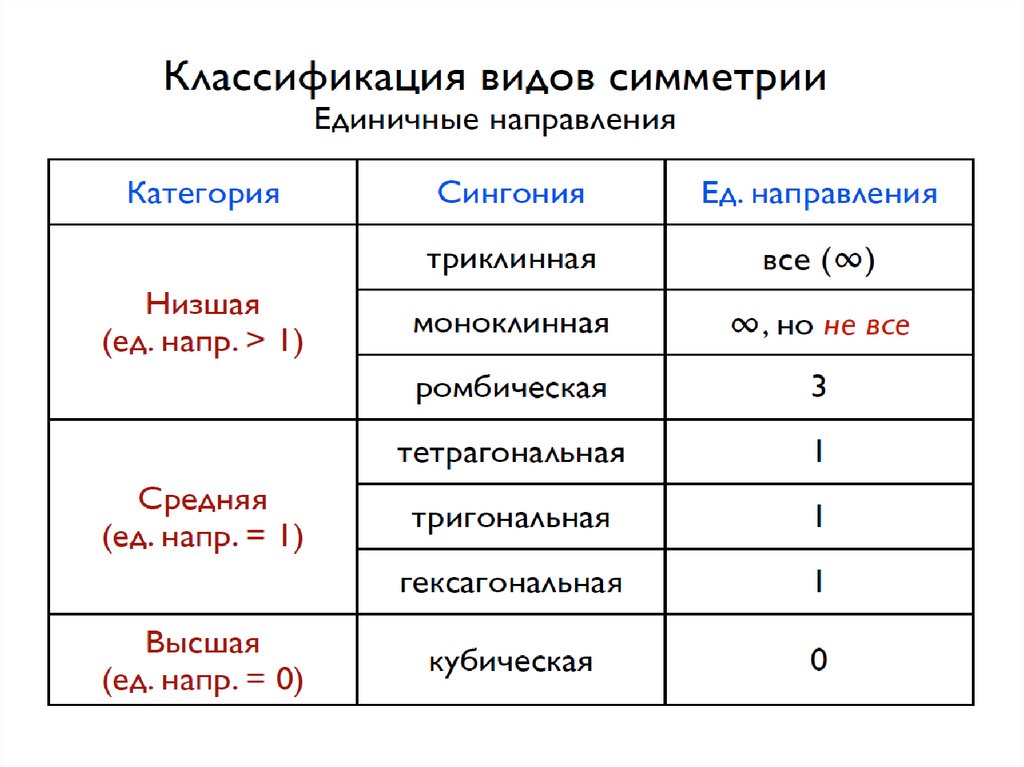
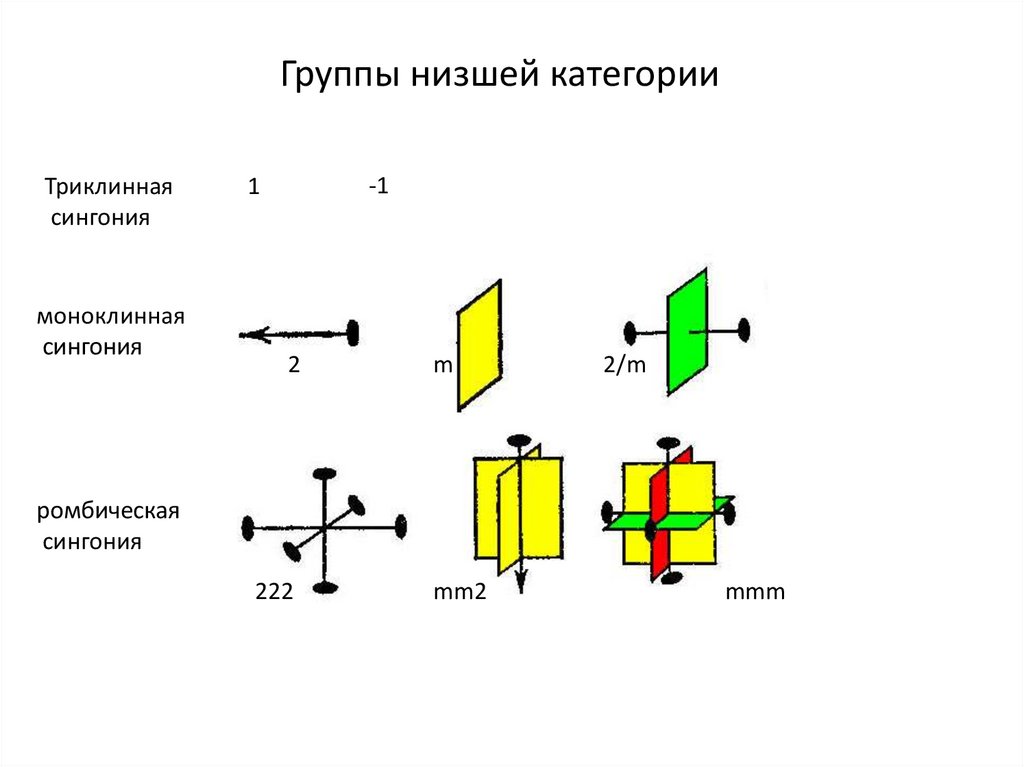
Группы низшей категорииТриклинная
сингония
моноклинная
сингония
-1
1
2
m
2/m
ромбическая
сингония
222
mm2
mmm
51.
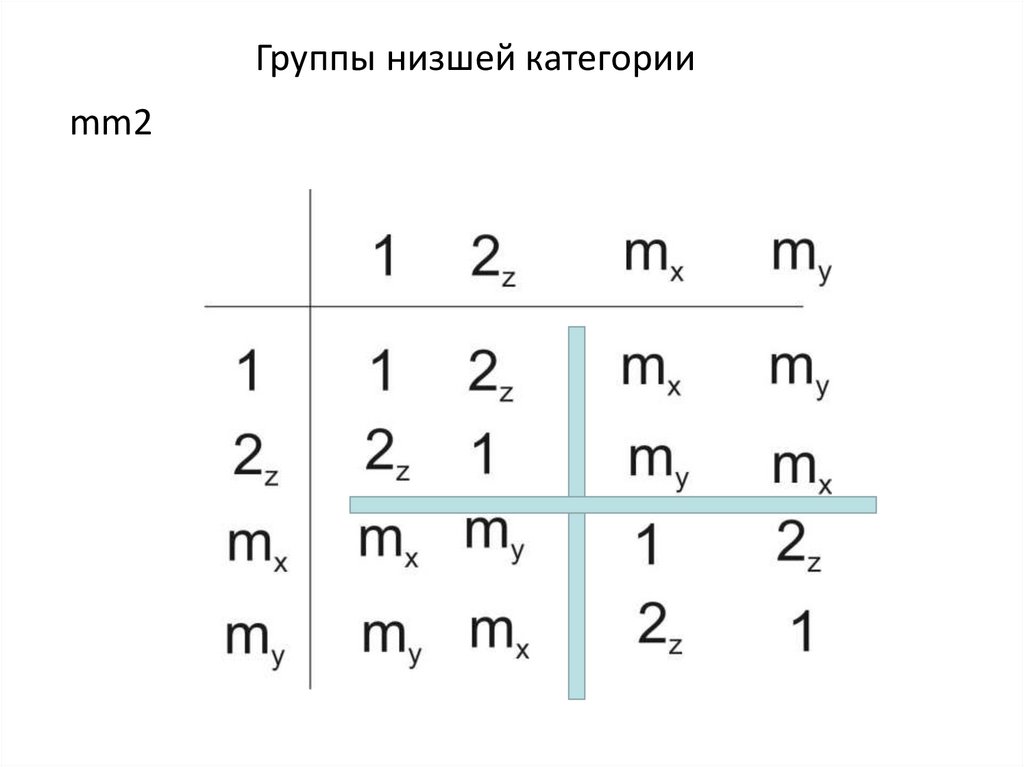
Группы низшей категорииmm2
1=
52.
Группы низшей категорииmm2
53.
Группы низшей категорииmm2
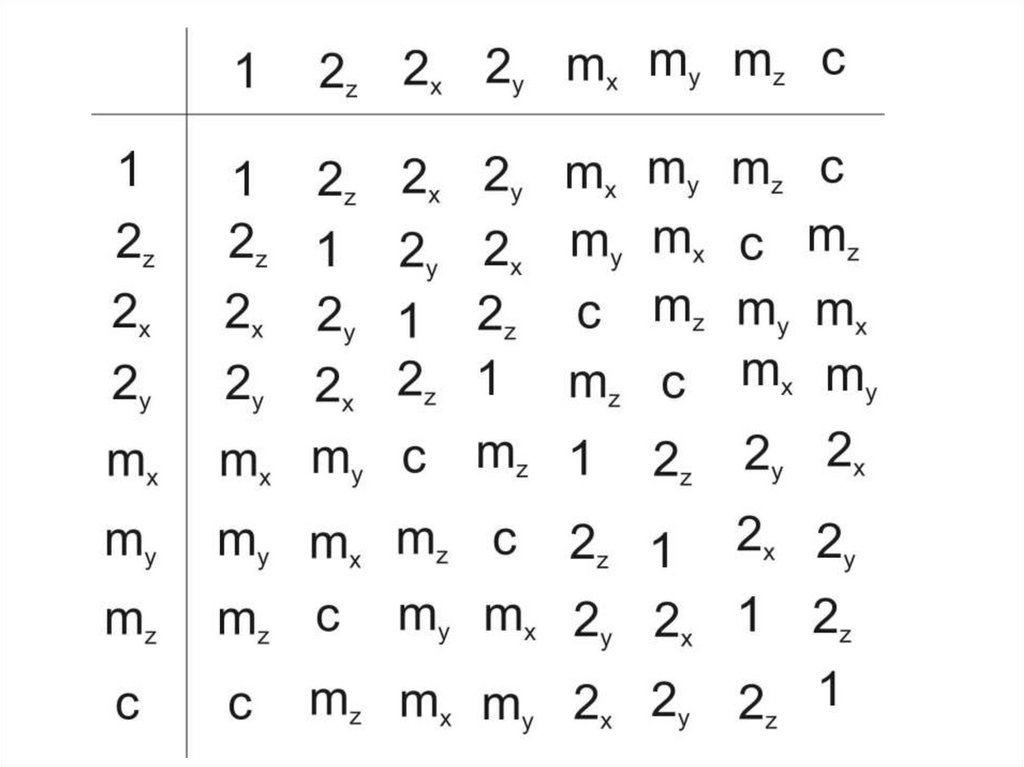
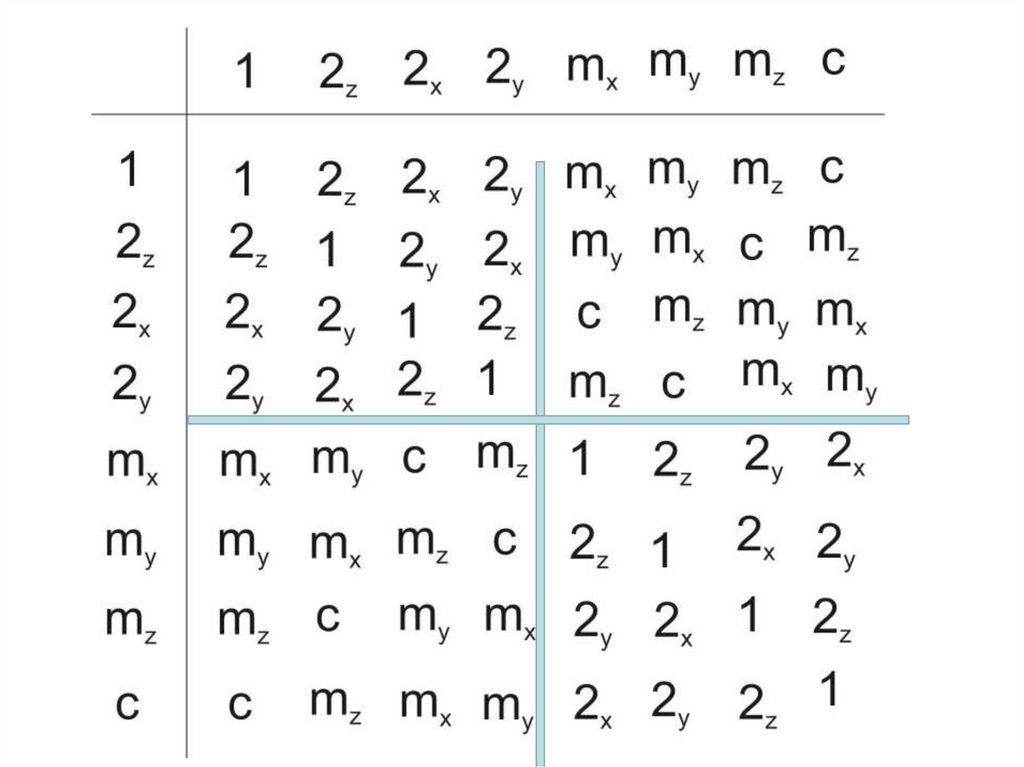
54.
mmmГруппы низшей категории
55.
56.
57.
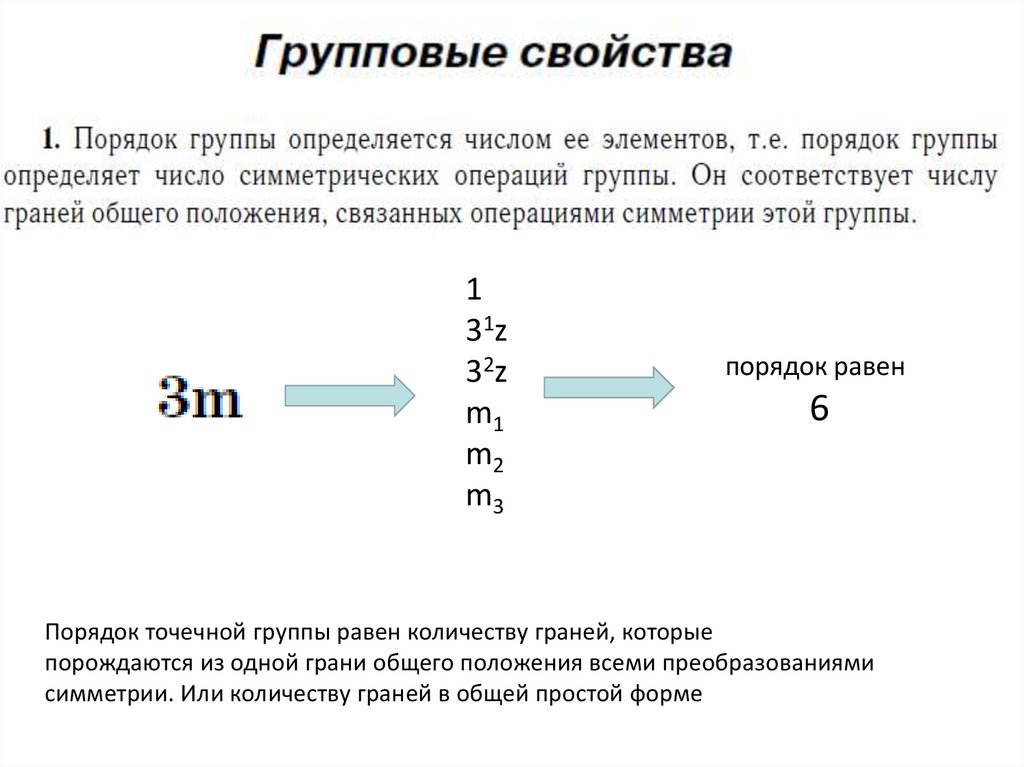
131z
32z
m1
m2
m3
порядок равен
6
Порядок точечной группы равен количеству граней, которые
порождаются из одной грани общего положения всеми преобразованиями
симметрии. Или количеству граней в общей простой форме
58.
59.
60.
Теорема ЛагранжаЕсли G – группа конечного порядка и H<G – нетривиальная
подгруппа, то порядок подгруппы |H| является делителем
порядка группы |G|:
|G| / |H| = j – индекс подгруппы H в группе G
Так группа mm2 четвертого порядка может иметь подгруппы
порядков
4/1 = 4, 4/2 =2, 4/4 =1
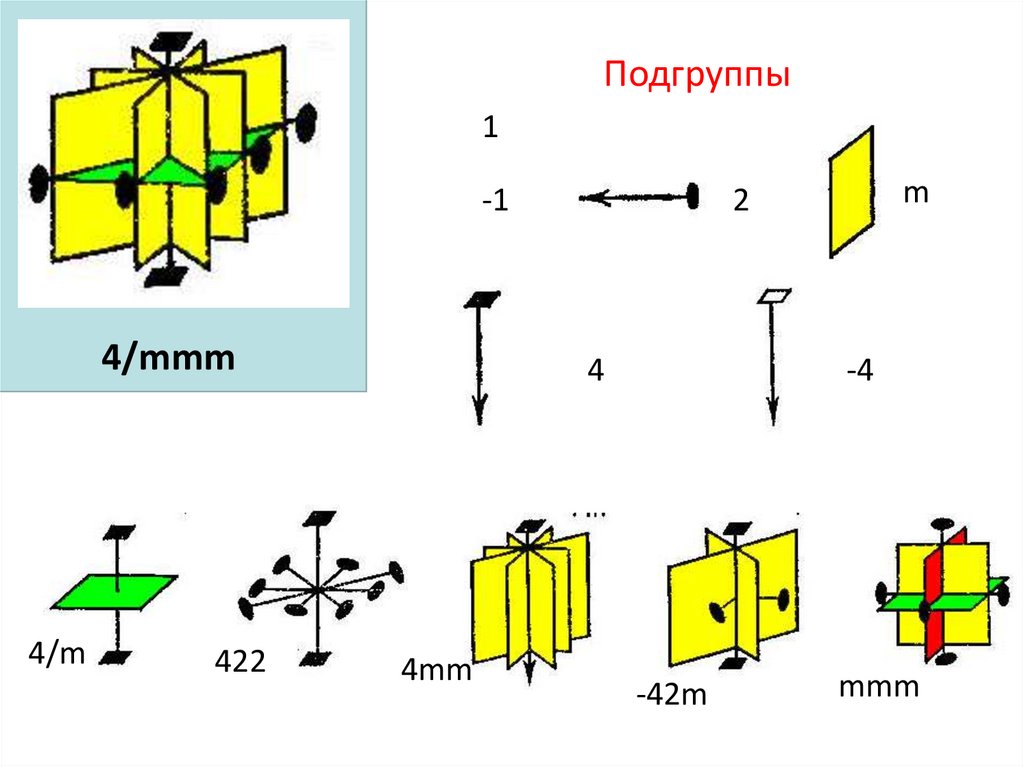
61.
Подгруппы1
-1
4/mmm
4/m
422
4
4mm
m
2
-4
-42m
mmm
62.
Группа является коммутативной или абелевой, если групповоедействие коммутативно для всех ее элементов.
gigj = gjgi
Из 32 точечных групп 16 являются коммутативными: 1, -1, 2, m,
2/m, 222, mm2, mmm, 4, -4, 4/m, 3, -3, 6, -6, 6/m.
mm2
63.
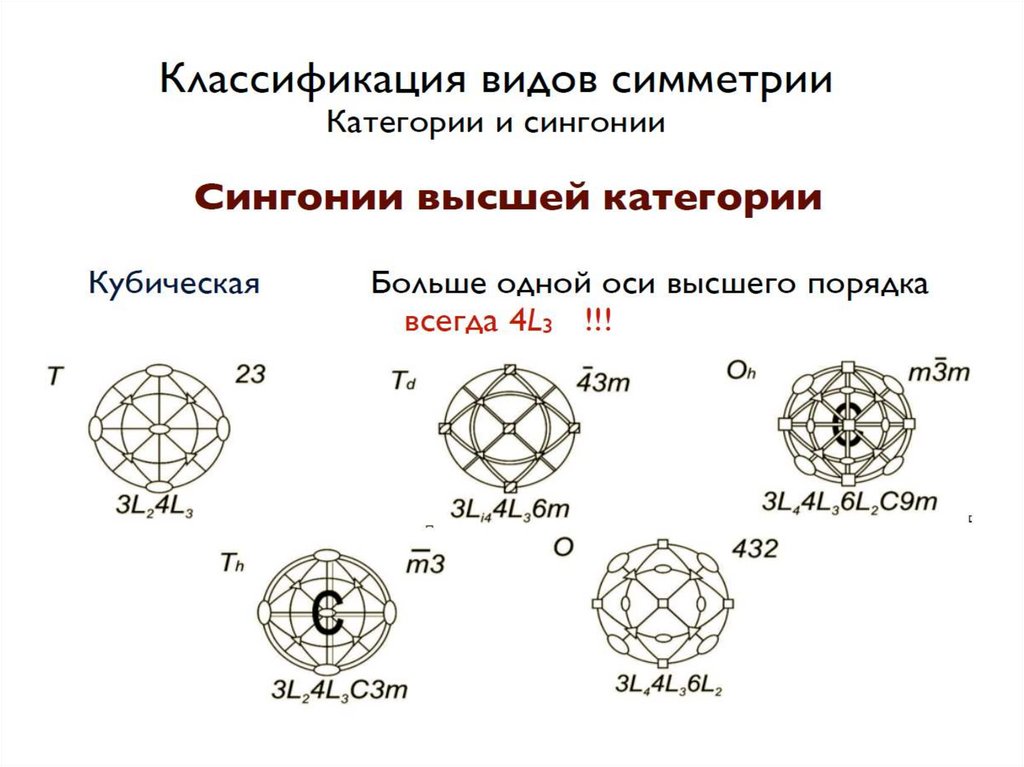
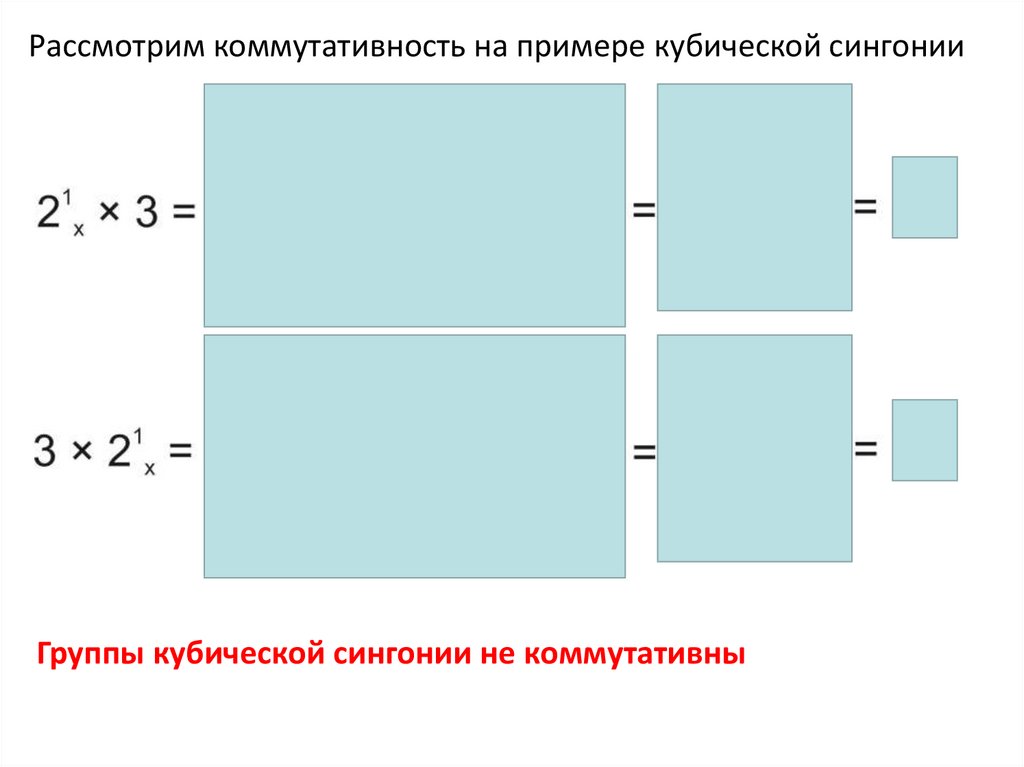
Рассмотрим коммутативность на примере кубической сингонииГруппы кубической сингонии не коммутативны
64.
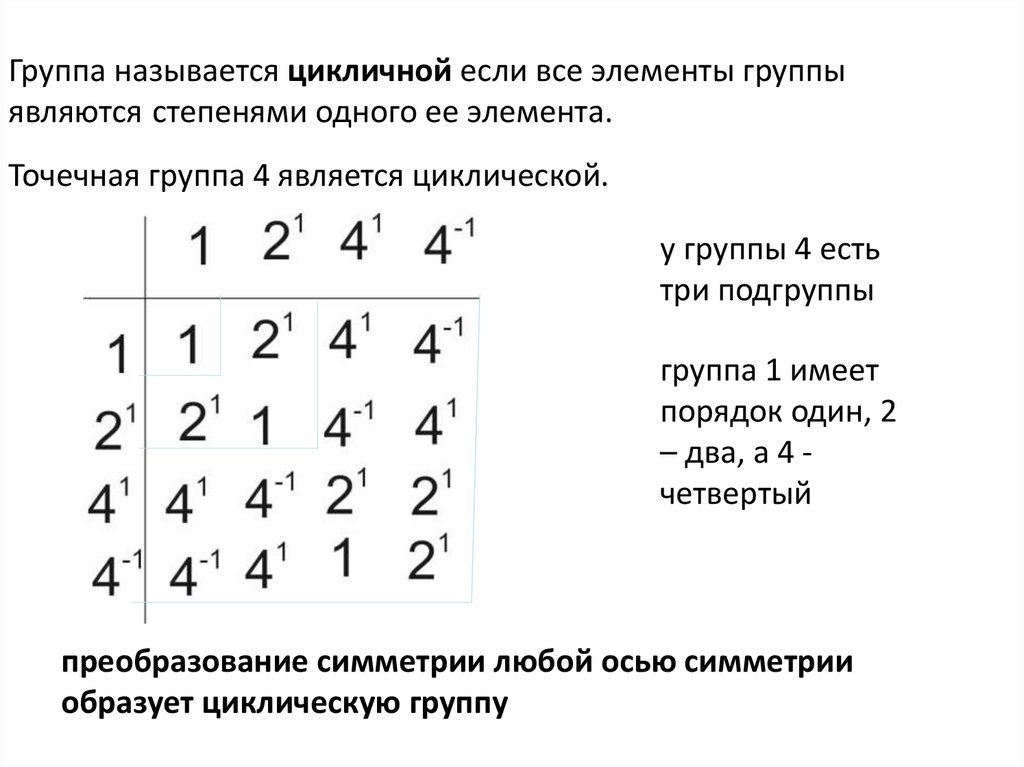
Группа называется цикличной если все элементы группыявляются степенями одного ее элемента.
Точечная группа 4 является циклической.
у группы 4 есть
три подгруппы
группа 1 имеет
порядок один, 2
– два, а 4 четвертый
преобразование симметрии любой осью симметрии
образует циклическую группу
65.
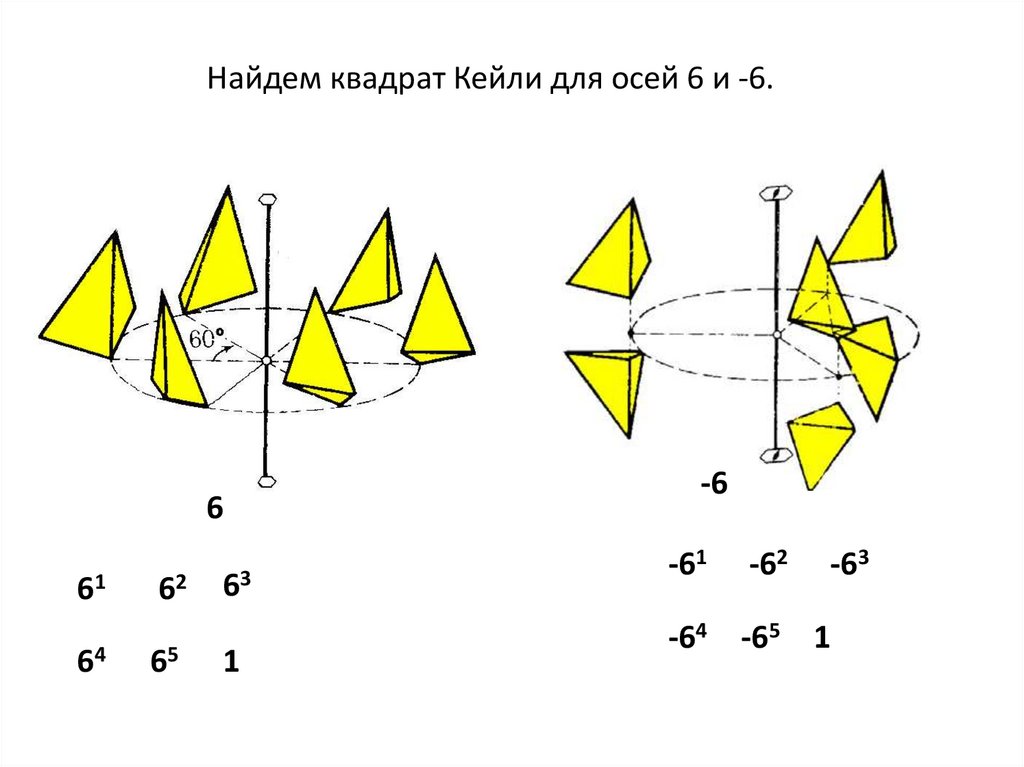
Найдем квадрат Кейли для осей 6 и -6.6
61
64
62
65
63
1
-6
-61
-62
-63
-64 -65 1
66.
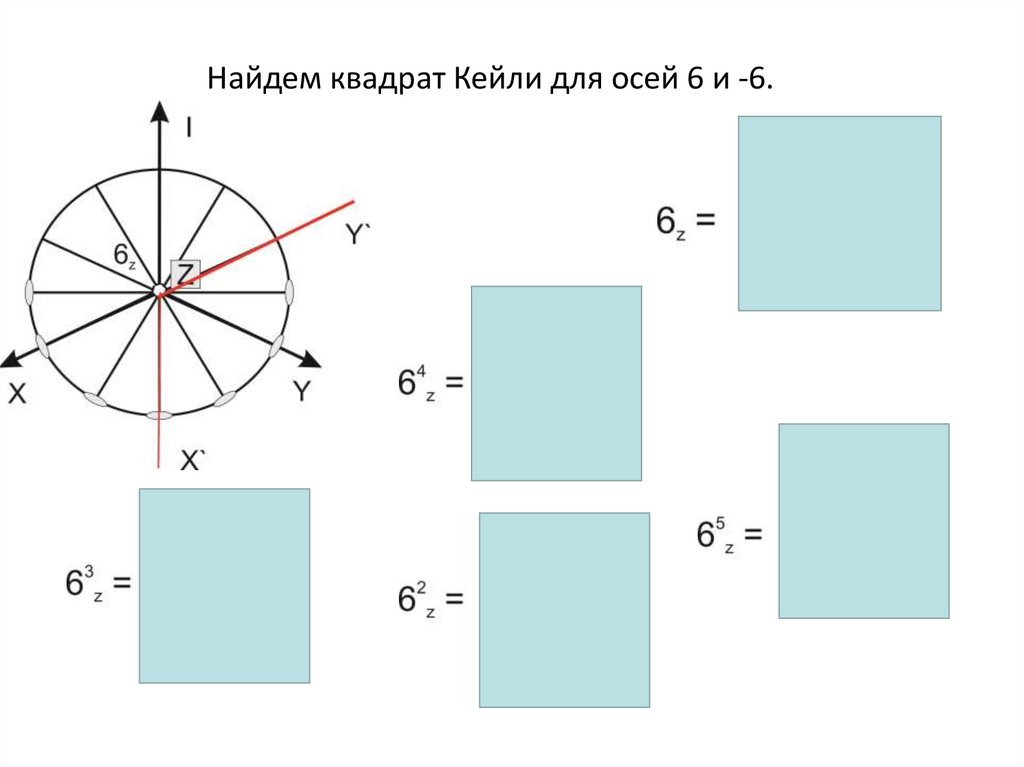
Найдем квадрат Кейли для осей 6 и -6.67.
Найдем квадрат Кейли для осей 6 и -6.68.
Вывод точечных групп симметриивыведем группы моноклинной и ромбической сингонии
в моноклинной сингонии есть только 2 и -2.
Добавим к квадрату Кейли для группы 2 (1, 2z) центр инверсии
69.
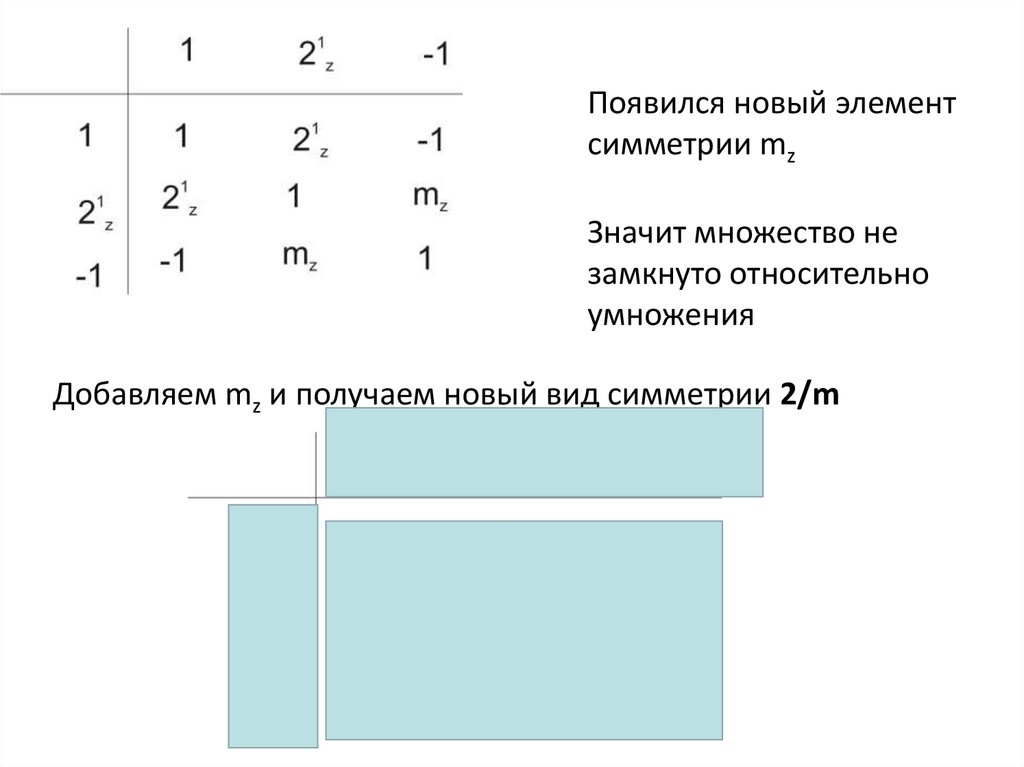
Появился новый элементсимметрии mz
Значит множество не
замкнуто относительно
умножения
Добавляем mz и получаем новый вид симметрии 2/m
70.
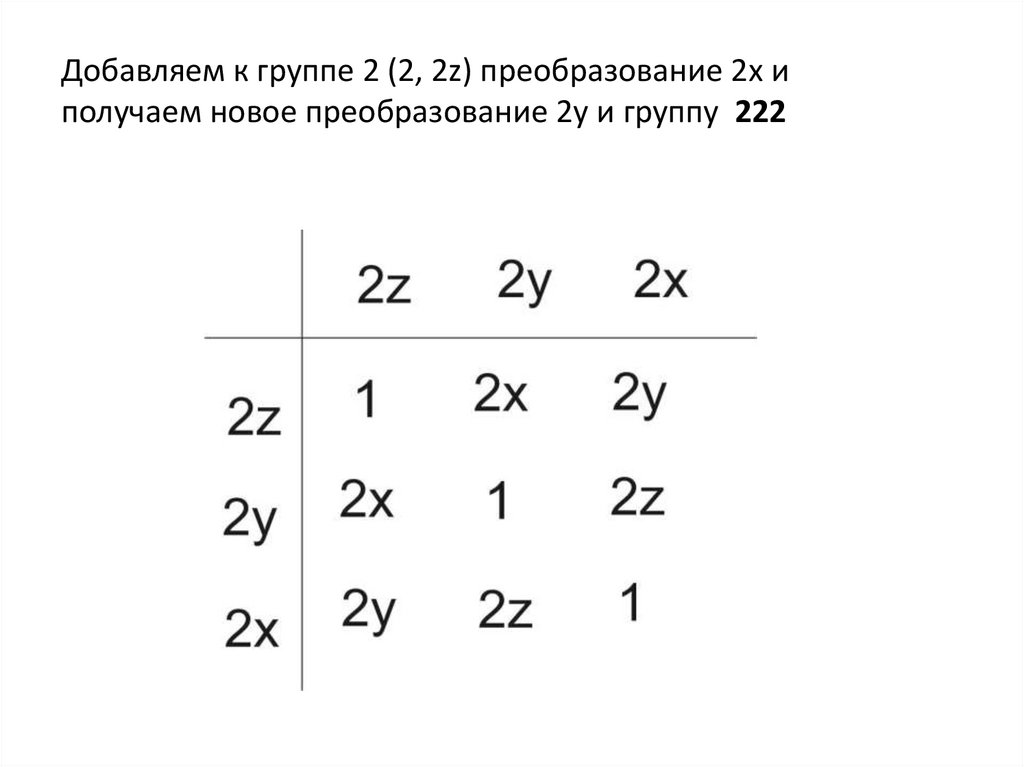
Добавляем к группе 2 (2, 2z) преобразование 2x иполучаем новое преобразование 2y и группу 222






















 Математика
Математика Химия
Химия