Цифровые системы управления

1. ЦИФРОВЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Лекция 1. Введение
Лекция 2. Дискретные системы
Лекция 3. Преобразование аналоговых
регуляторов
Лекция 4. Проектирование регуляторов для
дискретных систем
Лекция 5. Оптимальные системы
Лекция 6. Точные методы исследования
Лекция 7. Реализация цифровых
регуляторов
© К. Поляков, 2003

2. ЦИФРОВЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Лекция 1. Введение
Структуры и особенности цифровых
систем управления
Квантование сигналов и его свойства
Управляющая программа
Восстановление непрерывных сигналов
(экстраполяторы)
Преимущества и недостатки цифровых
систем управления
© К. Поляков, 2003

3. Литература

• Острём К., Виттенмарк Б. Системы управления
с ЭВМ, М.: Мир, 1987.
• Бесекерский В.А., Цифровые автоматические
системы, М.: Наука, 1976.
• Микропроцессорные системы автоматического
управления // Бесекерский В.А. и др., Л.:
Машиностроение, 1989.
• Б. Куо, Теория и проектирование цифровых
систем управления, М.: Машиностроение, 1986.
• Розенвассер Е.Н., Линейная теория цифрового
управления в непрерывном времени, М.: Наука,
1994.
© К. Поляков, 2003

4. Дополнительная литература

• Цыпкин Я.З., Теория импульсных систем, М.:
Физматгиз, 1963.
• Джури Э., Импульсные системы автоматического
регулирования, М.: Физматгиз, 1963.
• Ту Ю., Цифровые и импульсные системы
автоматического управления, М.:
Машиностроение, 1964.
• Чанг Ш., Синтез оптимальных систем
автоматического управления, М.:
Машиностроение, 1964.
• Изерман Р., Цифровые системы управления, М.:
Мир, 1984.
• Chen T., Francis B.A. Optimal sampled-data control
systems, NY: Springer-Verlag, 1995.
© К. Поляков, 2003

5. Поддержка курса

http://kpolyakov.narod.ru
http://kpolyakov.by.ru
• слайды к лекциям в формате PPT (для
Power Point) и PDF (для Acrobat Reader)
• примеры к лекциям
• методические указания для выполнения
лабораторной работы
• вопросы к экзамену
© К. Поляков, 2003

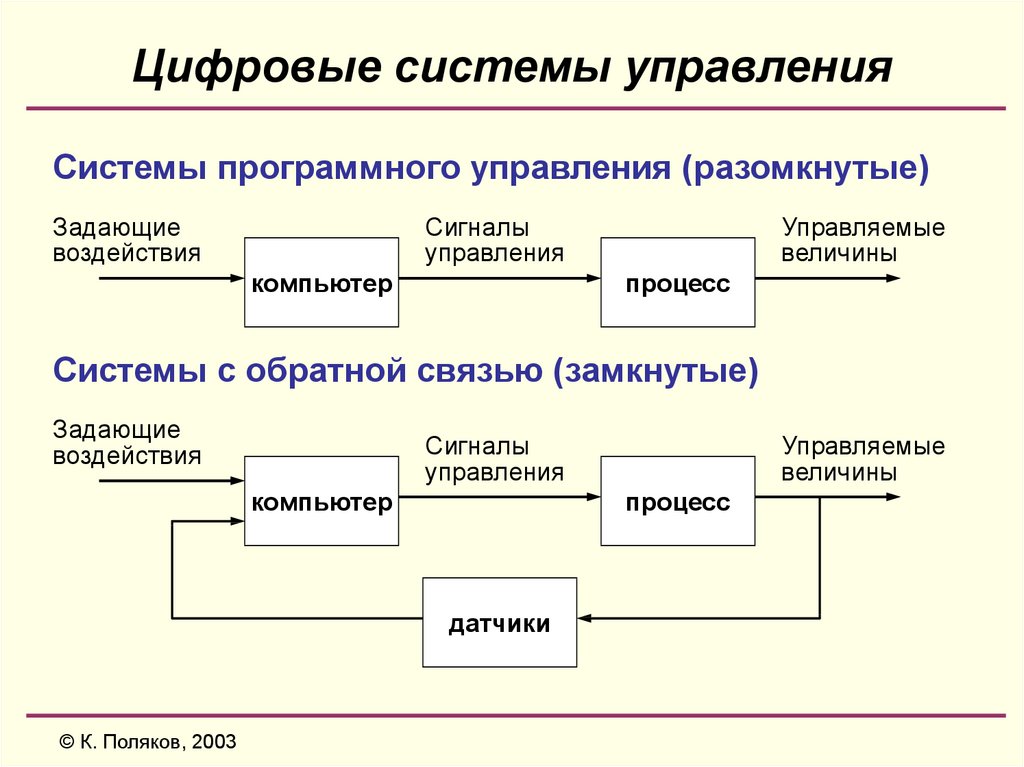
6. Цифровые системы управления

Системы программного управления (разомкнутые)
Задающие
воздействия
Сигналы
управления
компьютер
Управляемые
величины
процесс
Системы с обратной связью (замкнутые)
Задающие
воздействия
Сигналы
управления
компьютер
процесс
датчики
© К. Поляков, 2003
Управляемые
величины

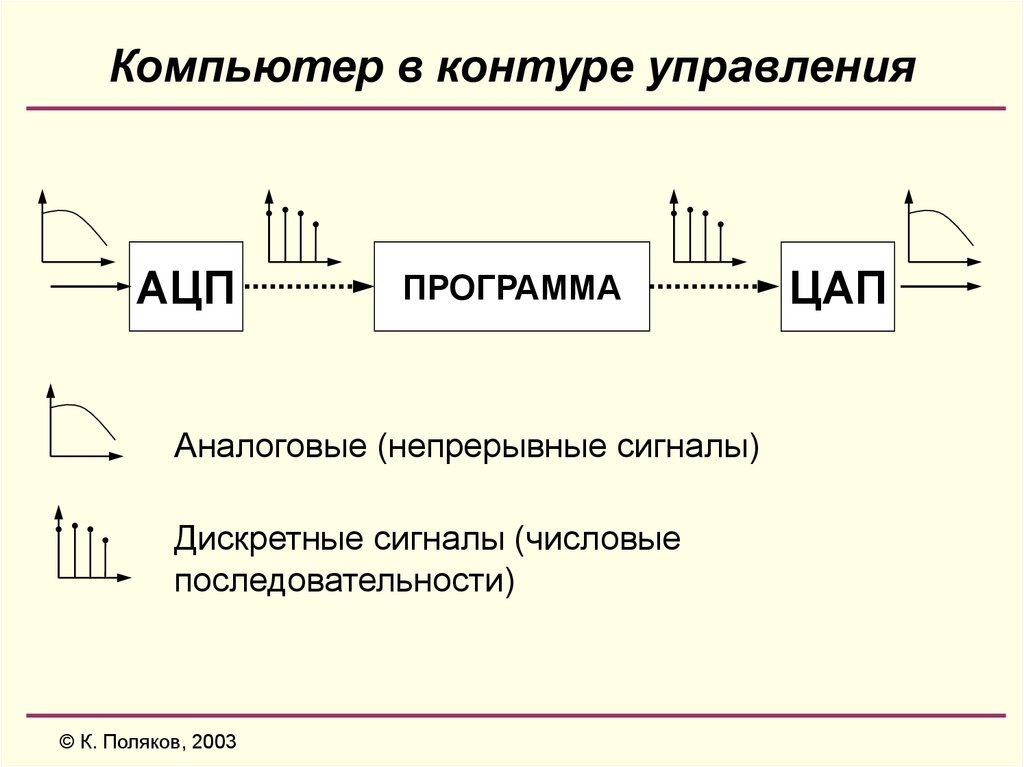
7. Компьютер в контуре управления

АЦП
ПРОГРАММА
Аналоговые (непрерывные сигналы)
Дискретные сигналы (числовые
последовательности)
© К. Поляков, 2003
ЦАП

8. Квантование

0
T 2T 3T 4T
t
• квантование по времени (с периодом T)
• квантование по уровню (8-12 бит)
© К. Поляков, 2003

9. Идеальный импульсный элемент

T
x (t )
x * (t )
(t kT)
k 0
x (t ) x(kT ) (t kT ) ,
*
k 0
0, t 0
(t )
,
, t 0
© К. Поляков, 2003
(t ) dt 1, f (t ) (t ) dt f ( )

10.

Преобразование Лапласа для x*(t)
Импульсный сигнал
x* (t )
x(kT ) (t kT ) ,
k 0
Преобразование Лапласа для x*(t)
0
0 k 0
X * ( s ) x* (t ) e st dt
x(kT ) e
k 0
© К. Поляков, 2003
ksT
st
x
(
kT
)
(
t
kT
)
e
dt

11.

Свойство периодичности
Частота квантования
2
s
T
Периодичность X*(s) с периодом j s
k 0
k 0
X * ( s mj s ) x(kT ) e k ( s mj s )T x(kT ) e ksT e mj sT
e mj sT e 2 mj cos 2 m j sin 2 m 1.
X * ( s mj s ) X * ( s),
X * ( j mj s ) X * ( j )
© К. Поляков, 2003
m целое

12. Частотные свойства при квантовании

Преобразование Фурье для x(t)
X ( j ) x(t ) e j t dt
0
Преобразование Фурье для x*(t)
0
k 0
X * ( j ) x* (t ) e j t dt x(kT ) e kj T
Связь спектров непрерывного и импульсного
сигналов (X(j ) убывает быстрее, чем 1/ )
1
X * ( j mj s )
X ( j kj s )
T k
X * ( j mj s ) X * ( j ),
© К. Поляков, 2003
m целое

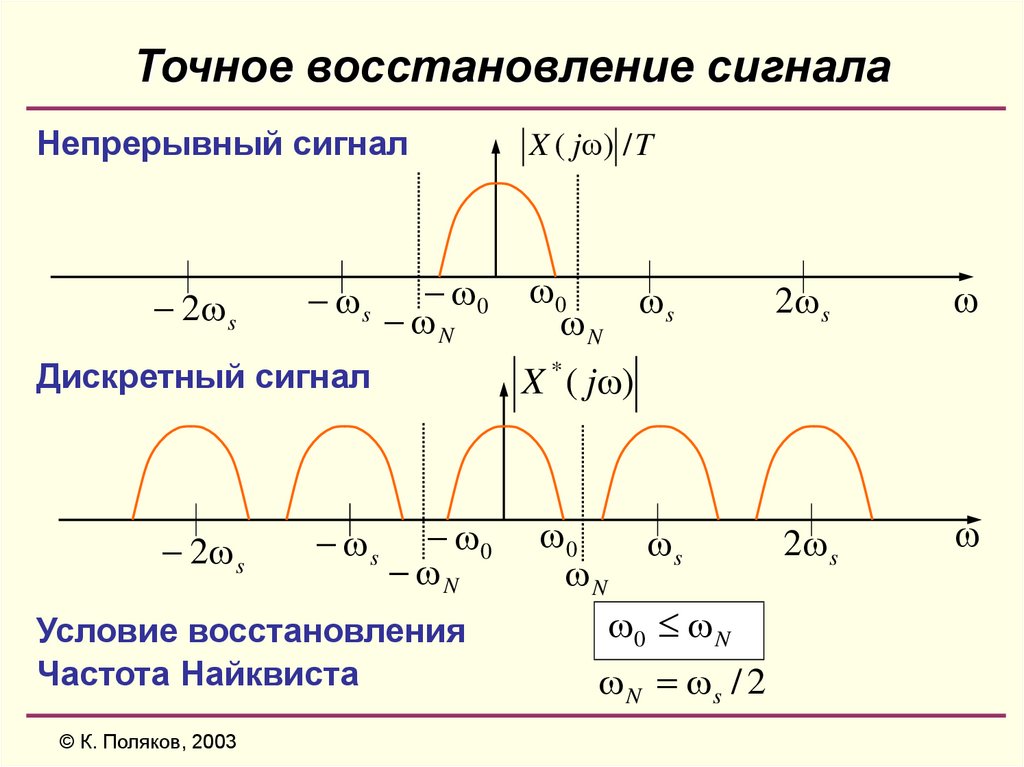
13. Точное восстановление сигнала

Непрерывный сигнал
2 s
s
0
N
s
0
N
Условие восстановления
Частота Найквиста
© К. Поляков, 2003
0
s
N
2 s
2 s
X * ( j )
Дискретный сигнал
2 s
X ( j ) / T
0
N
s
0 N
N s / 2

14. Теорема Котельникова-Шеннона

Непрерывный сигнал, преобразование Фурье
которого равно нулю вне интервала
(- 0, 0), однозначно представляется своими
значения в равноотстоящих точках, если частота
квантования больше 0. Непрерывный сигнал
может быть получен из дискретного по формуле
sin s (t kT ) / 2
x(t ) x(kT )
s (t kT ) / 2
k
© К. Поляков, 2003

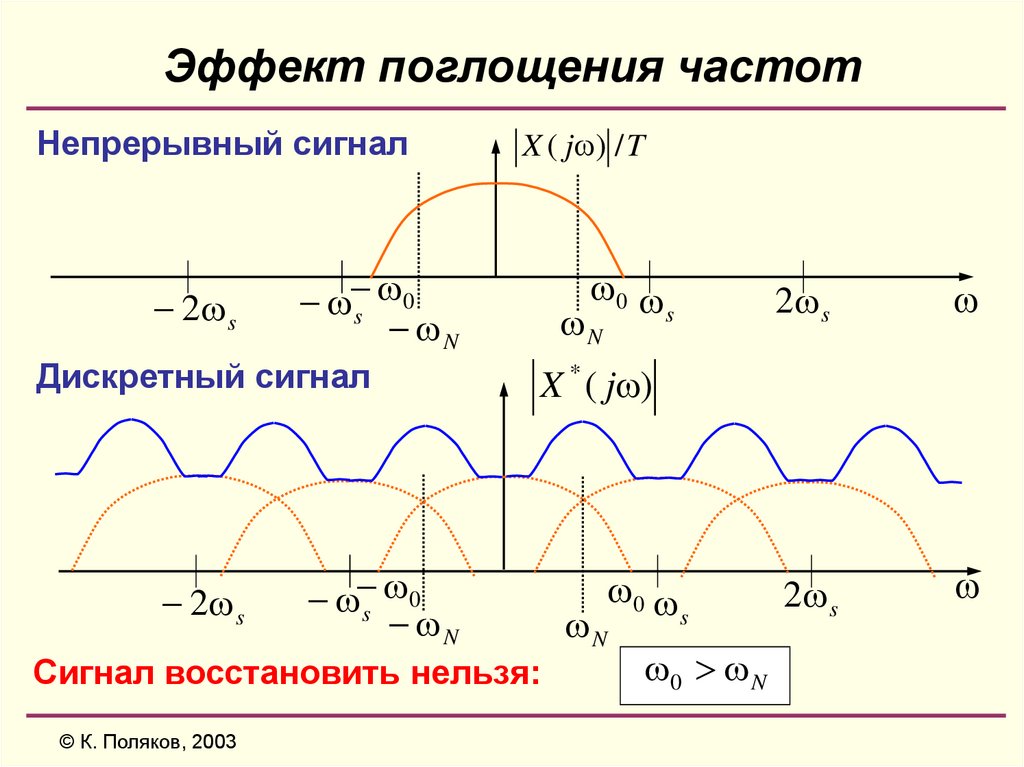
15. Эффект поглощения частот

Непрерывный сигнал
2 s
s 0
N
Дискретный сигнал
2 s
X ( j ) / T
0
s
N
2 s
X * ( j )
s 0
N
Сигнал восстановить нельзя:
© К. Поляков, 2003
2 s
0
N
s
0 N

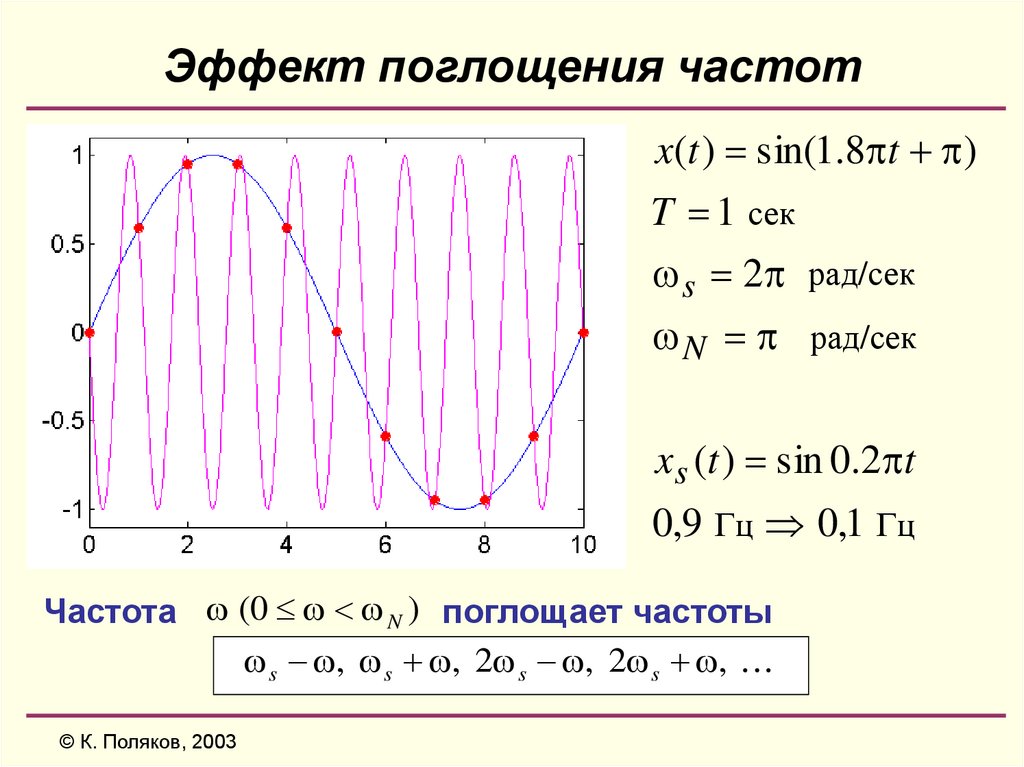
16. Эффект поглощения частот

x(t ) sin(1.8 t )
T 1 сек
s 2 рад/сек
N рад/сек
x s (t ) sin 0.2 t
0,9 Гц 0,1 Гц
Частота (0 N ) поглощает частоты
s , s , 2 s , 2 s ,
© К. Поляков, 2003

17. Чем плохо поглощение частоты?

• спектры реальных сигналов не равны нулю при
N
• высокочастотные помехи проявляются на низких
частотах после квантования
Меры борьбы
• использование предварительной фильтрации
(фильтр низкой частоты)
• выбор частоты квантования 2 max
где max - частота среза «самого быстрого» звена
© К. Поляков, 2003

18. Описание работы компьютера

y[n]
x[n]
*
ПРОГРАММА
x (t )
y * (t )
Алгоритм обработки сигнала
y[n] ( x[n], x[n 1], , y[n 1], y[n 2], )
© К. Поляков, 2003

19. Линейные законы управления

Скользящее среднее (СС) (MA – moving average)
y[n] b0 x[n] b1 x[n 1] bk x[n k ]
Авторегрессионный процесс (АР) (AR – autoregression)
y[n] a1 y[n 1] ak y[n k ] x[n]
Авторегрессионный процесс со скользящим средним
(АРСС) (ARMA)
y[n] a1 y[n 1] ak y[n k ] b0 x[n] b1 x[n 1] bk x[n k ]
© К. Поляков, 2003

20. Операторная запись

y[n] a1 y[n 1] ak y[n k ] b0 x[n] b1 x[n 1] bk x[n k ]
Оператор обратного сдвига (назад), или z-1
y[n 1] y[n], y[n k ] k y[n]
(1 a1 ak k ) y (b0 b1 bk k ) x
b0 b1 bk k
y
x C ( ) x
k
1 a1 ak
Передаточная функция регулятора
b0 b1 bk k
C ( )
k
1 a1 ak
© К. Поляков, 2003

21. Оператор прямого сдвига

Оператор прямого сдвига (вперед)
y[n 1] z y[n], y[n k ] z k y[n]
будущие значения – физически нереализуем!
Передаточная функция регулятора
k 1
b0 z b1 z bk
C ( z) k
z a1 z k 1 ak
k
© К. Поляков, 2003

22. Восстановление сигнала

Фиксатор нулевого порядка (ZOH – zero order hold)
y*
y
запаздывание на 0,5T
T
0
y * (t ) y[k ] (t kT )
k 0
© К. Поляков, 2003
t
t
0
y (t ) y[k ], 0 t T

23. Фиксатор нулевого порядка

Импульсная характеристика
h(t )
1
h0 (t ) 1(t ) 1(t T )
1
t
T
t
Передаточная функция
sT
1
e
H 0 ( s ) 1(t ) 1(t T ) e st dt
s
0
© К. Поляков, 2003

24. Фиксатор нулевого порядка

Частотная характеристика
© К. Поляков, 2003
1 e j T
H 0 ( j )
j

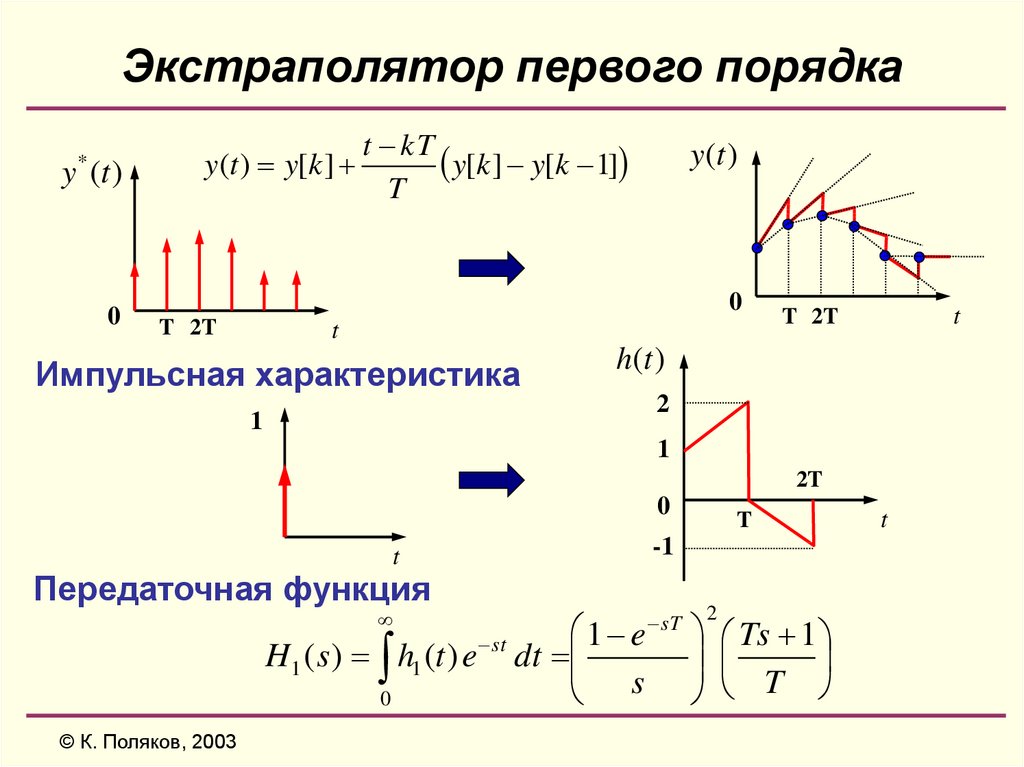
25. Экстраполятор первого порядка

*
y (t )
0
y(t ) y[k ]
t kT
y[k ] y[k 1]
T
y (t )
0
T 2T
t
Импульсная характеристика
t
T 2T
h(t )
2
1
1
2T
0
-1
t
Передаточная функция
H1 ( s ) h1 (t ) e
0
© К. Поляков, 2003
T
st
1 e
dt
s
sT
2
Ts 1
T
t

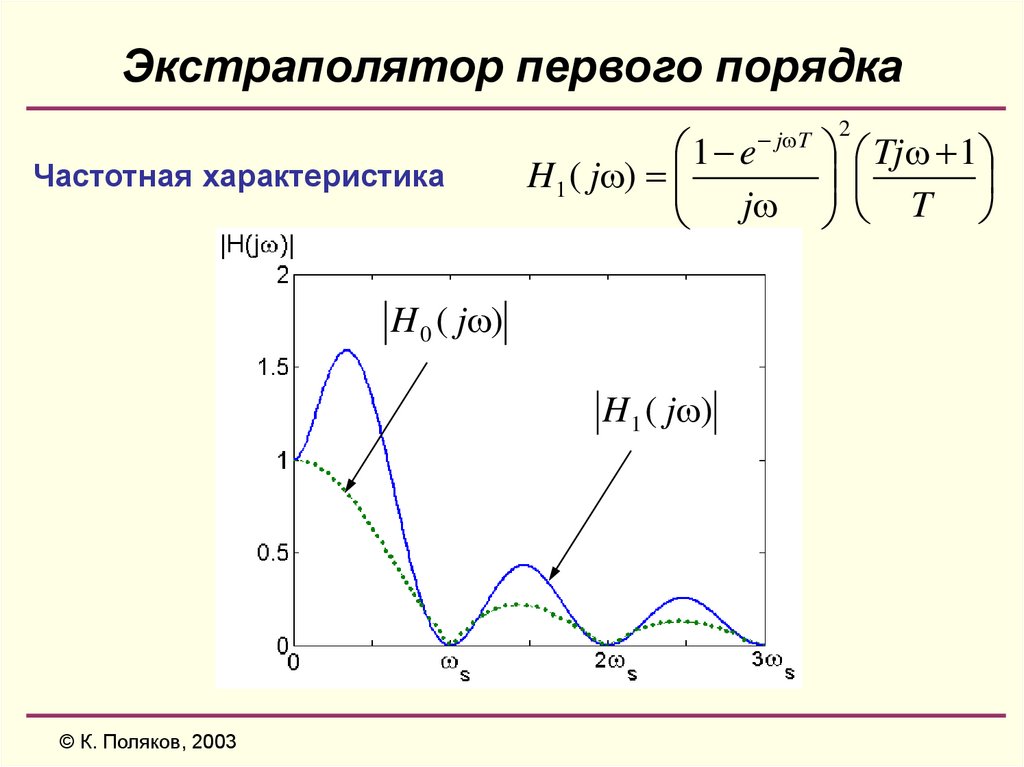
26. Экстраполятор первого порядка

1 e
H1 ( j )
j
j T
Частотная характеристика
H 0 ( j )
H 1 ( j )
© К. Поляков, 2003
2
Tj 1
T

27. Преимущества цифровых систем

Стандартная аппаратура
Нет дрейфа параметров
Гибкость, легкость настройки
Возможность реализации сложных
законов управления
• Возможность адаптации
© К. Поляков, 2003

28. Недостатки цифровых систем

• Дискретизация сигналов приводит к потере
точности
• Теряется информация о входных сигналах
между моментами квантования
• Между моментами квантования система
не управляется: устойчивость!
• Высокочастотные составляющие в сигнале
управления
© К. Поляков, 2003

29. Методы исследования цифровых систем

• сведение к непрерывной стационарной
системе (квантование игнорируется!)
• сведение к дискретной стационарной
системе (рассматриваются только
моменты квантования!)
• точные методы (нужен специальный
математический аппарат!)
© К. Поляков, 2003