Похожие презентации:
Многогранники
1. Многогранники
• Многогранник –замкнутая
пространственная
фигура ограниченая
плоскими
многоугольниками
2.
3.
Пирамидамногогранник, у которого одна грань - основание
(произвольный многоугольник), а остальные грани
(боковые) - треугольники с общей вершиной,
называемой вершиной пирамиды.
Правильная
пирамида
4.
Призмамногогранник, у которого основания – равные
многоугольники с соответственно параллельными сторонами.
Боковые грани призмы - параллелограммы.
Прямая призма – призма, у которой ребра боковых граней
перпендикулярны основанию.
Прямая
призма
Параллелепипед
5.
Призматоиды (антипризма)Призматоид ― многогранник, две грани которого
(основания призматоида) лежат в параллельных
плоскостях, а остальные являются треугольниками
или трапециями, причём у треугольников одна
сторона, а у трапеций оба основания являются
сторонами оснований призматоида.
6.
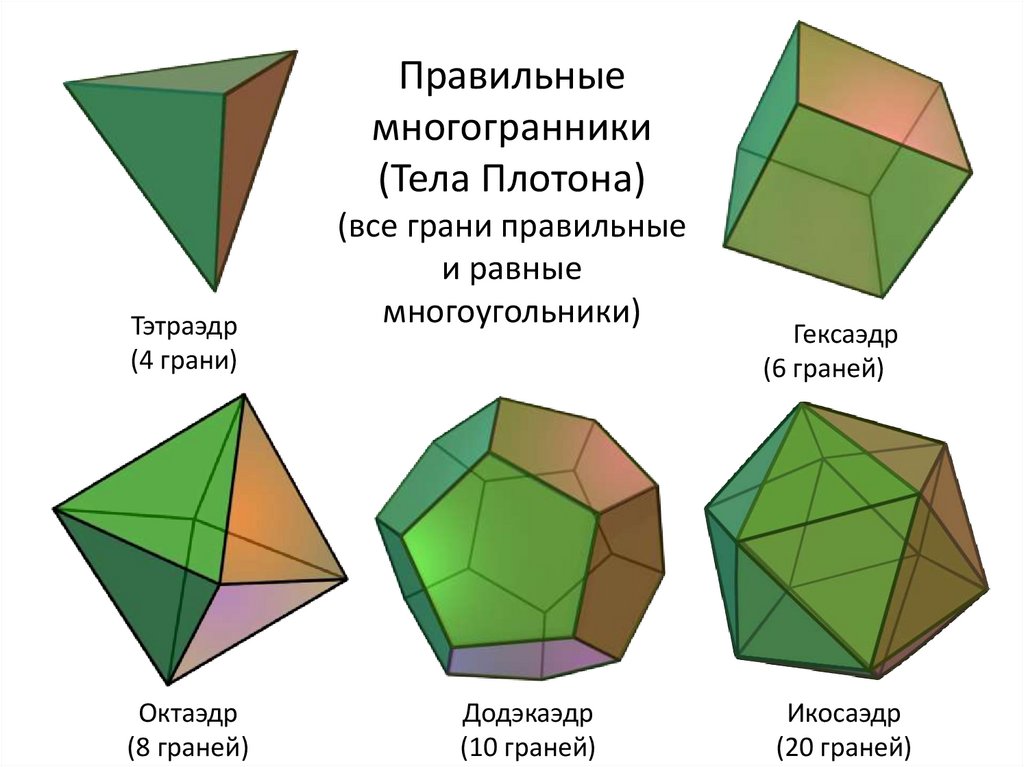
Правильныемногогранники
(Тела Плотона)
Тэтраэдр
(4 грани)
Октаэдр
(8 граней)
(все грани правильные
и равные
многоугольники)
Додэкаэдр
(10 граней)
Гексаэдр
(6 граней)
Икосаэдр
(20 граней)
7.
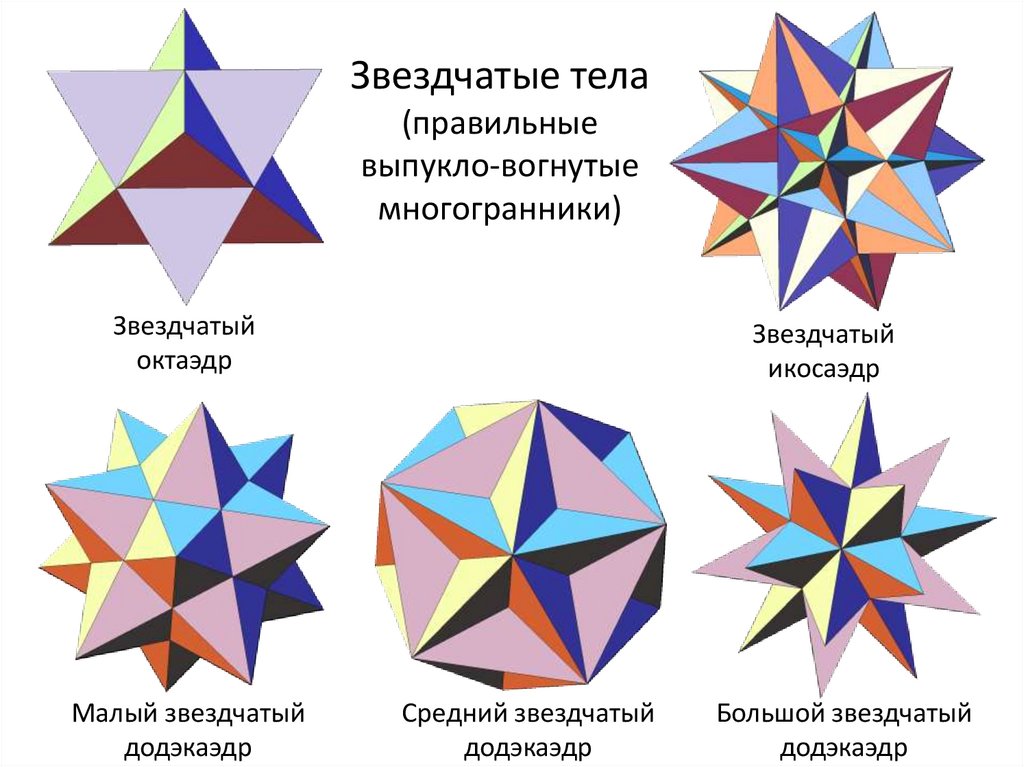
Звездчатые тела(правильные
выпукло-вогнутые
многогранники)
Звездчатый
октаэдр
Малый звездчатый
додэкаэдр
Звездчатый
икосаэдр
Средний звездчатый
додэкаэдр
Большой звездчатый
додэкаэдр
8.
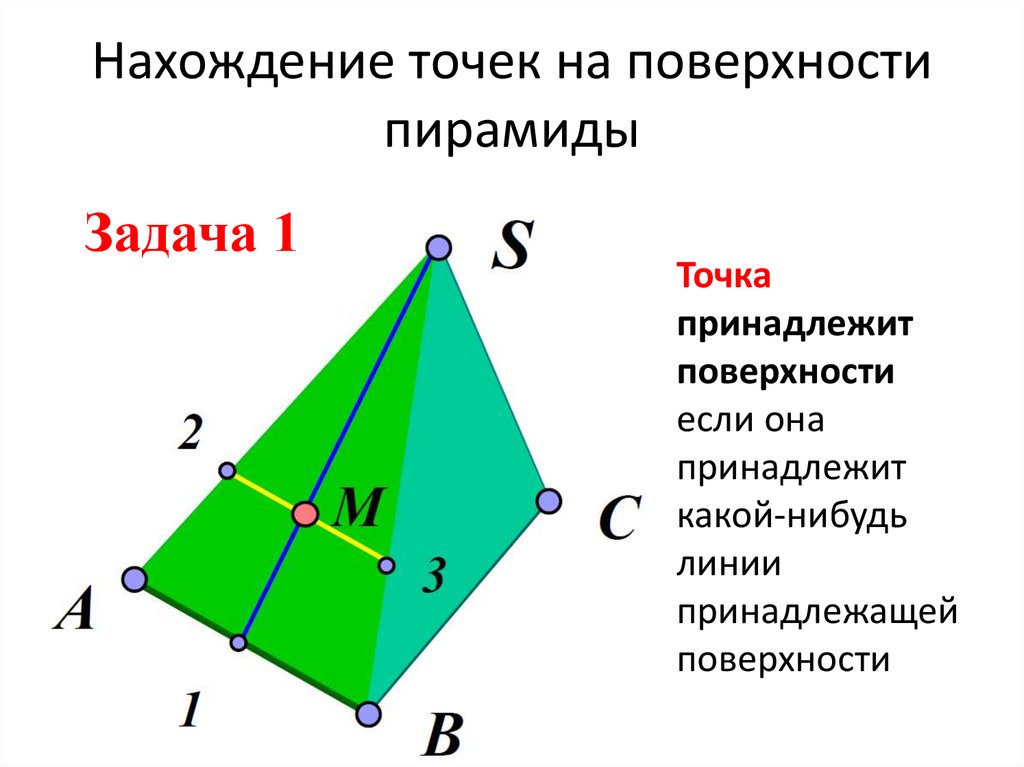
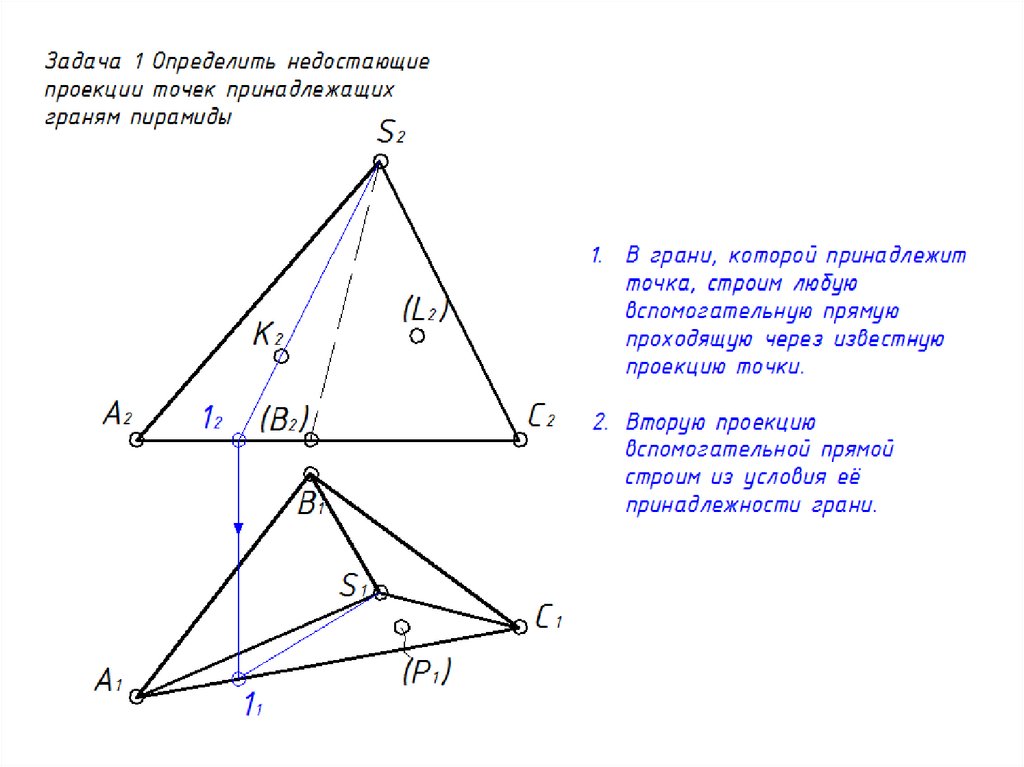
9. Нахождение точек на поверхности пирамиды
Задача 1Точка
принадлежит
поверхности
если она
принадлежит
какой-нибудь
линии
принадлежащей
поверхности
10.
11.
12.
13.
14.
15.
16.
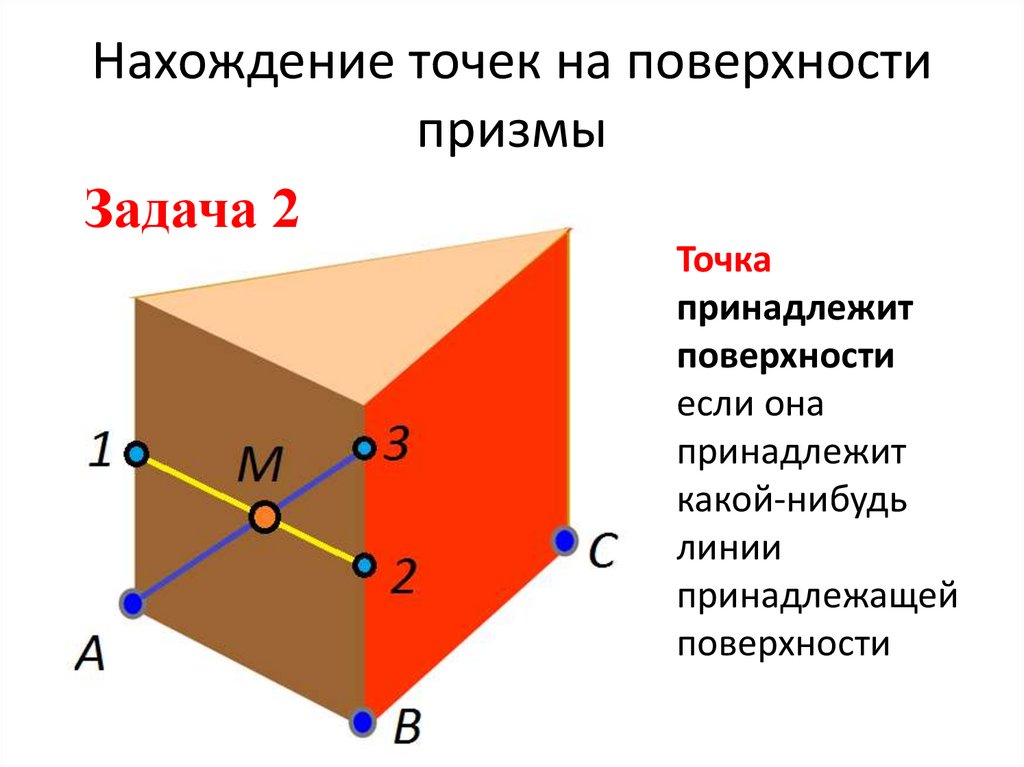
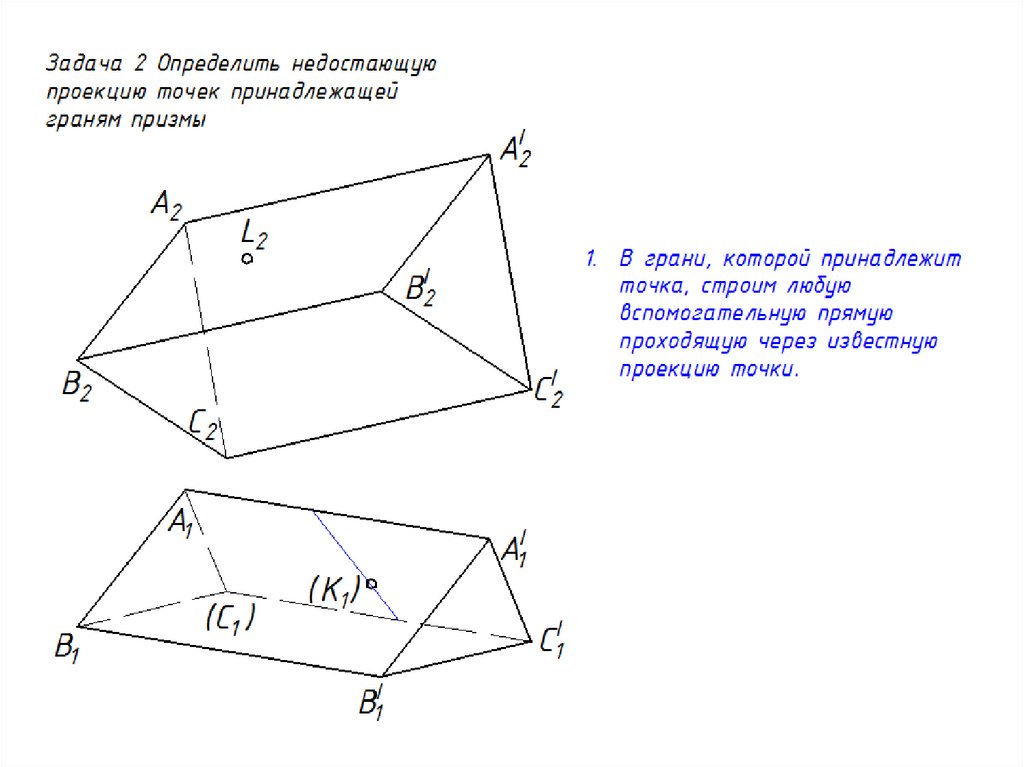
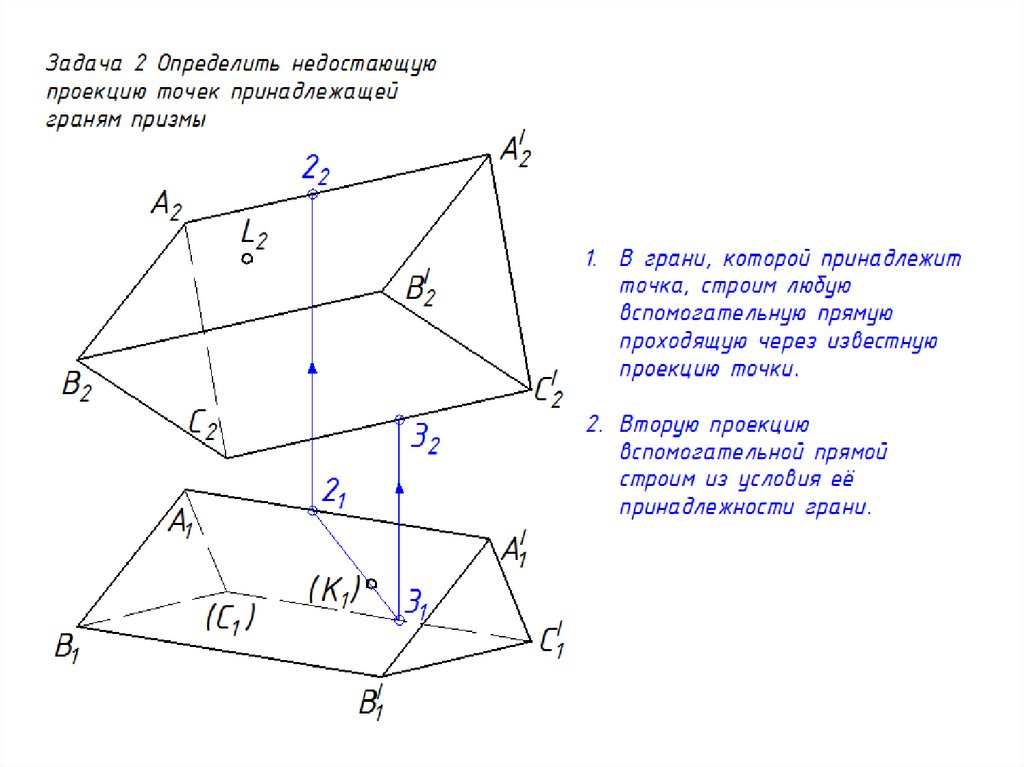
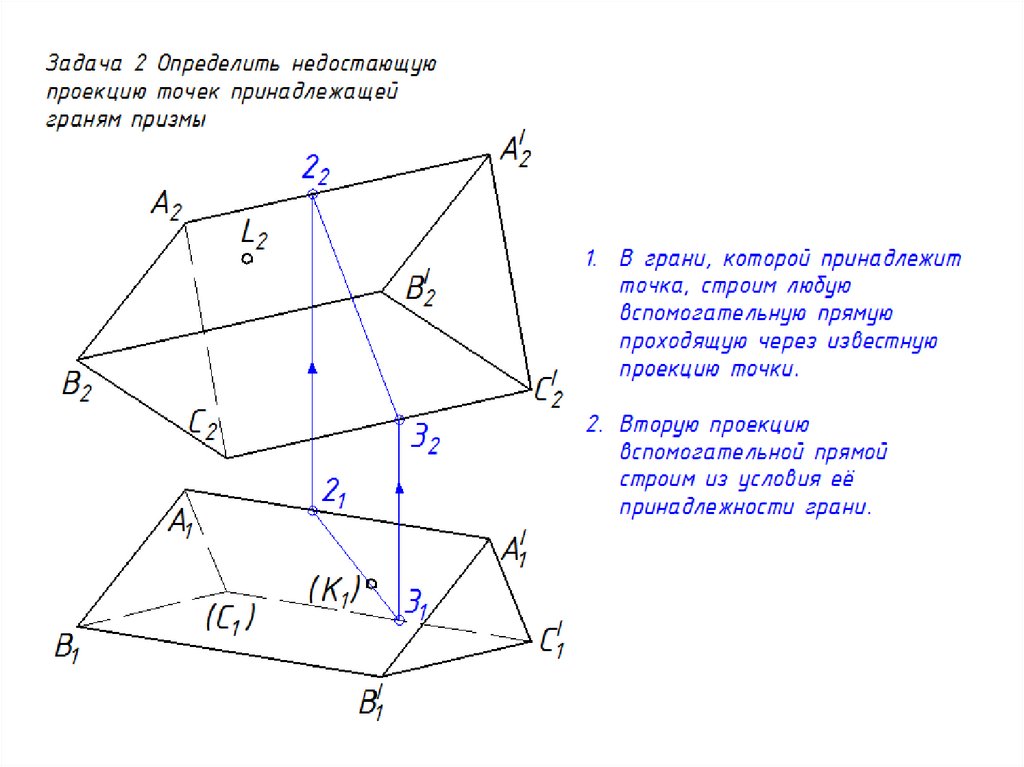
17. Нахождение точек на поверхности призмы
Задача 2Точка
принадлежит
поверхности
если она
принадлежит
какой-нибудь
линии
принадлежащей
поверхности
18.
19.
20.
21.
22.
23.
24.
25.
26.
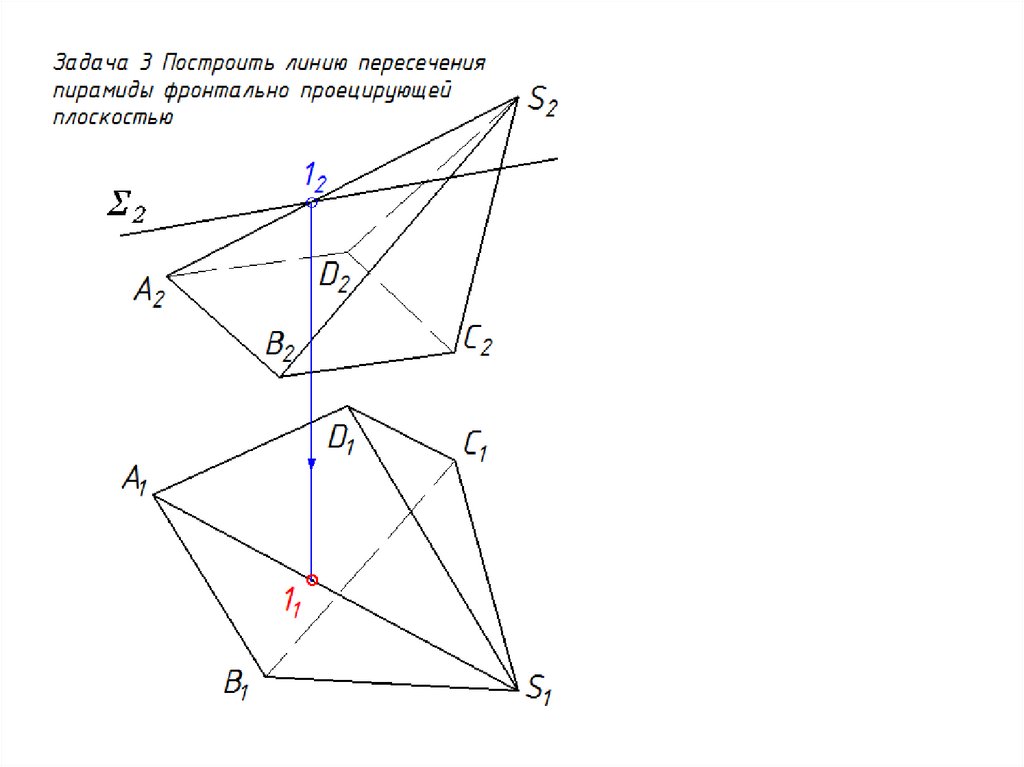
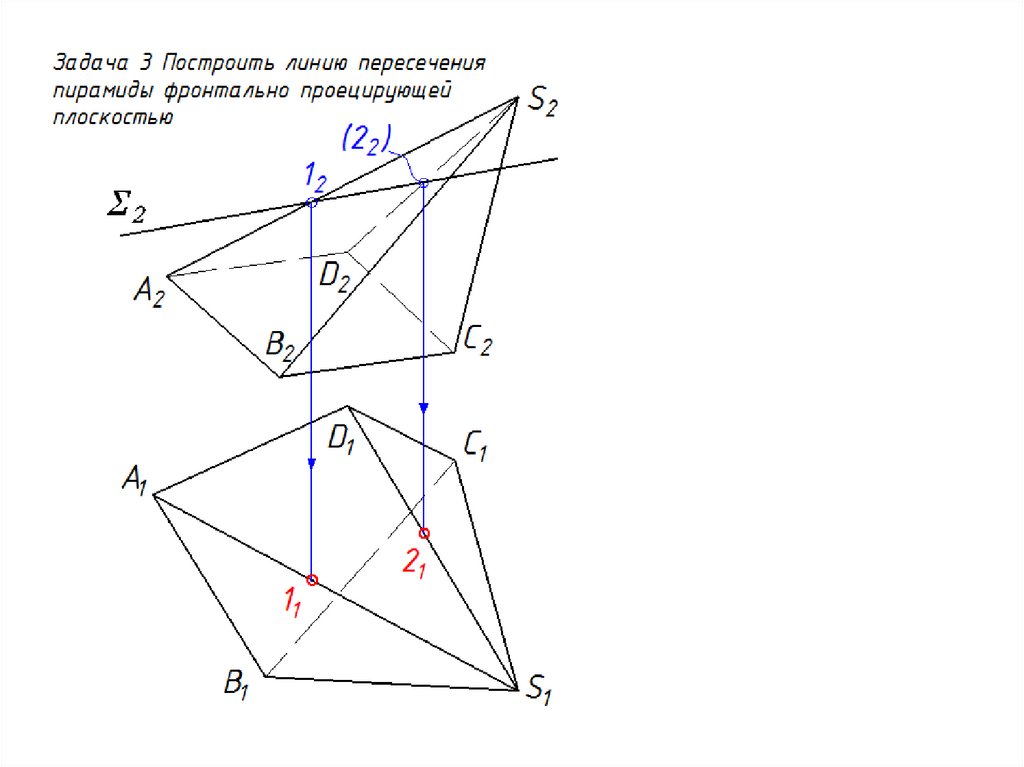
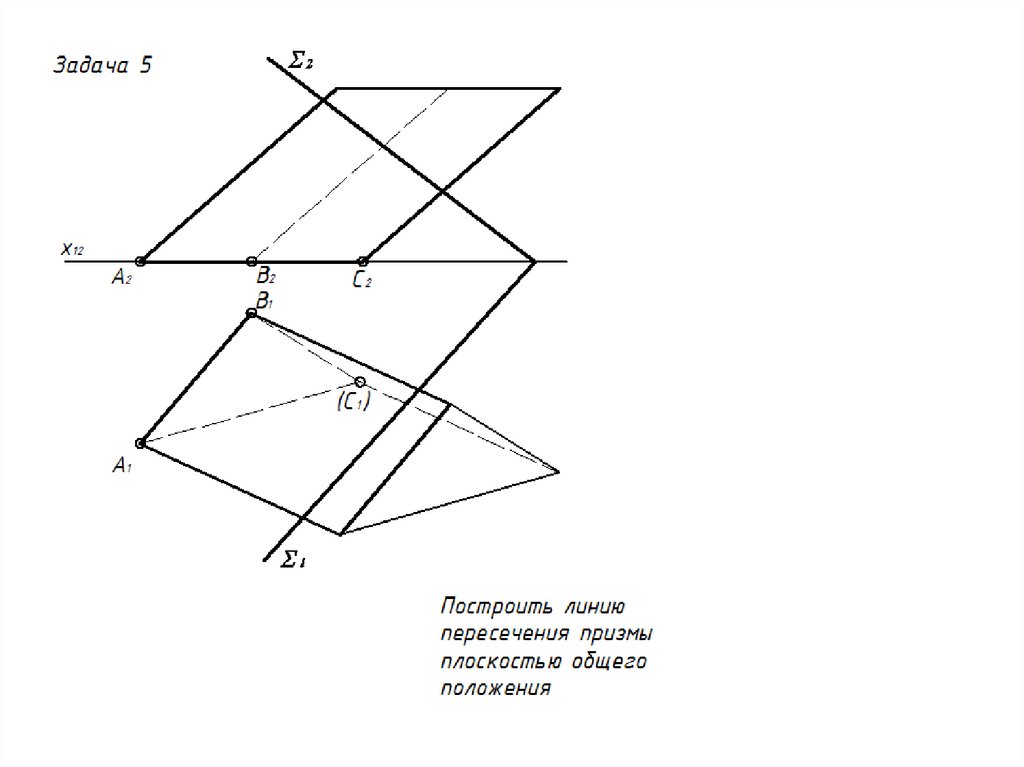
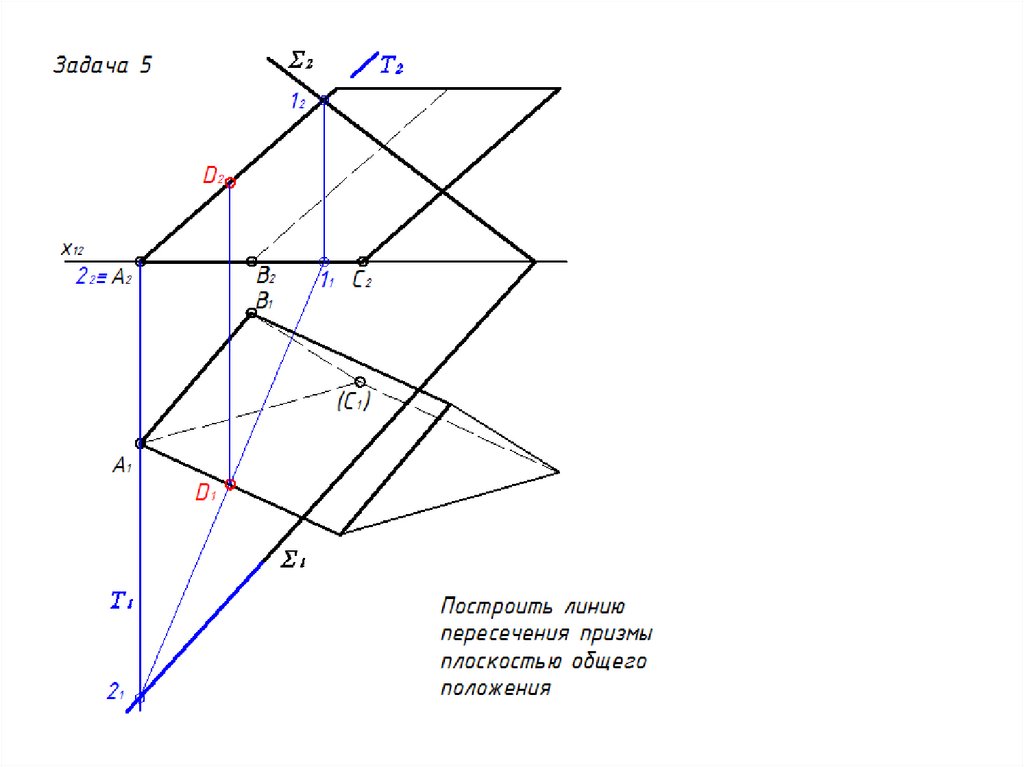
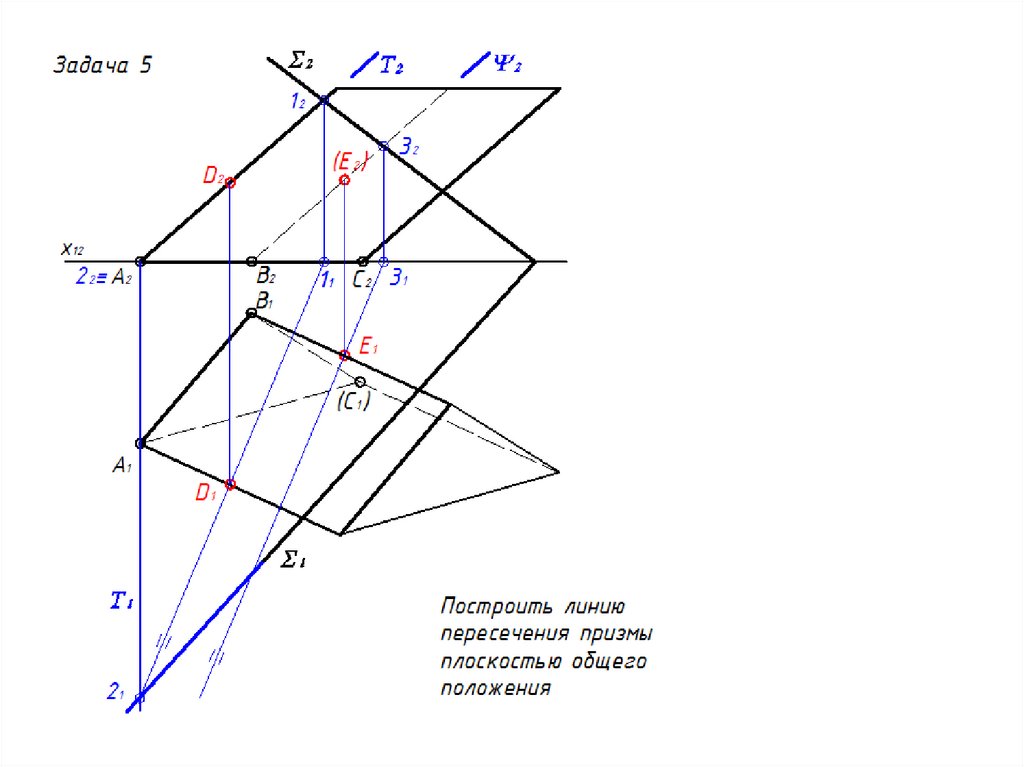
27. Сечение многогранника проецирующей плоскостью
Задача 328.
29.
30.
31.
32.
33.
34.
35.
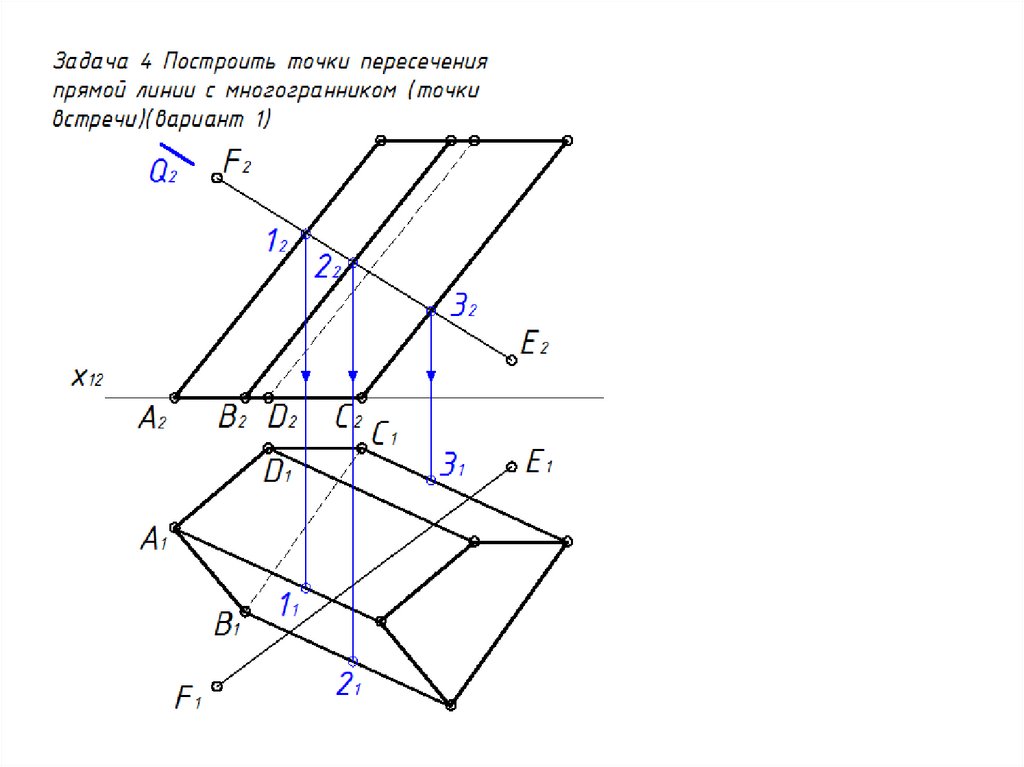
36. Пересечение многогранника прямой линией
Задача 4Алгоритм
1. Заключаем прямую во
вспомогательную плоскость (Ϭ)
(удобнее выбрать плоскость
частного положения)
2. Находим сечение
многогранника плоскостью
(ломаная KLM)
3. Находим точки пересечения
исходная прямая линия (а) и
сечения многогранника (KLM)
(т.к. они находятся в одной
плоскости Ϭ)
4. Определяем видимость,
(методом конкурирующих
точек или с помощью анализа
положения граней
многогранника)
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
Для лучешейнаглядности на
слайде убраны
вспомогательные
точки
47.
Для лучешейнаглядности на
слайде убраны
вспомогательные
точки
48.
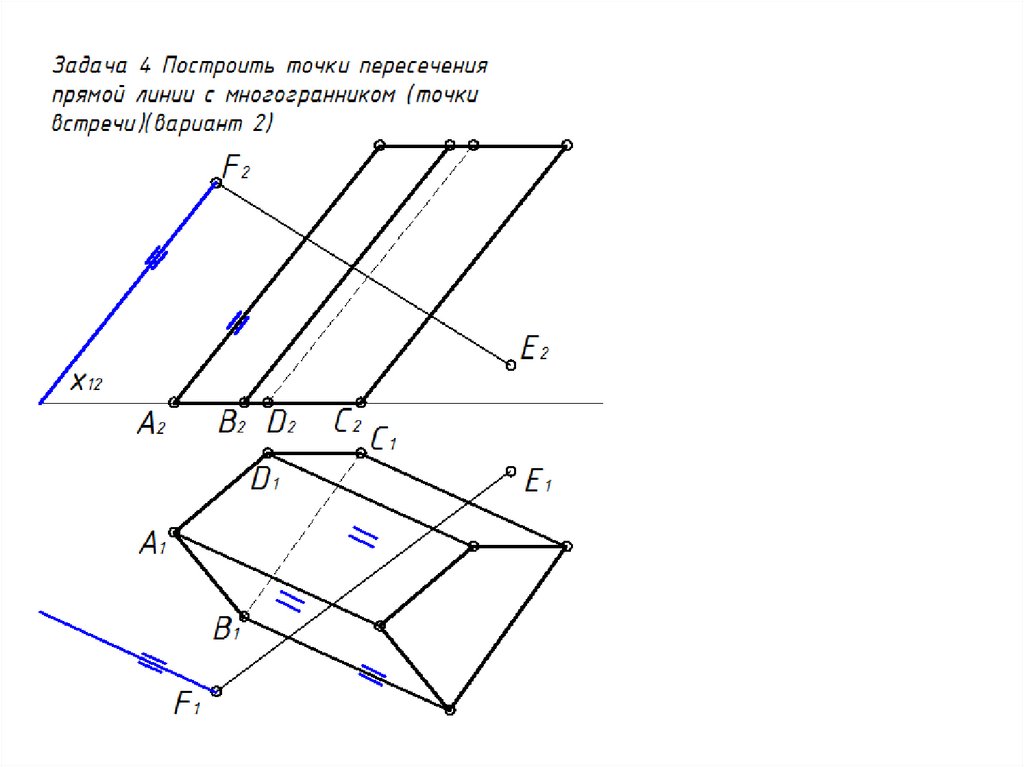
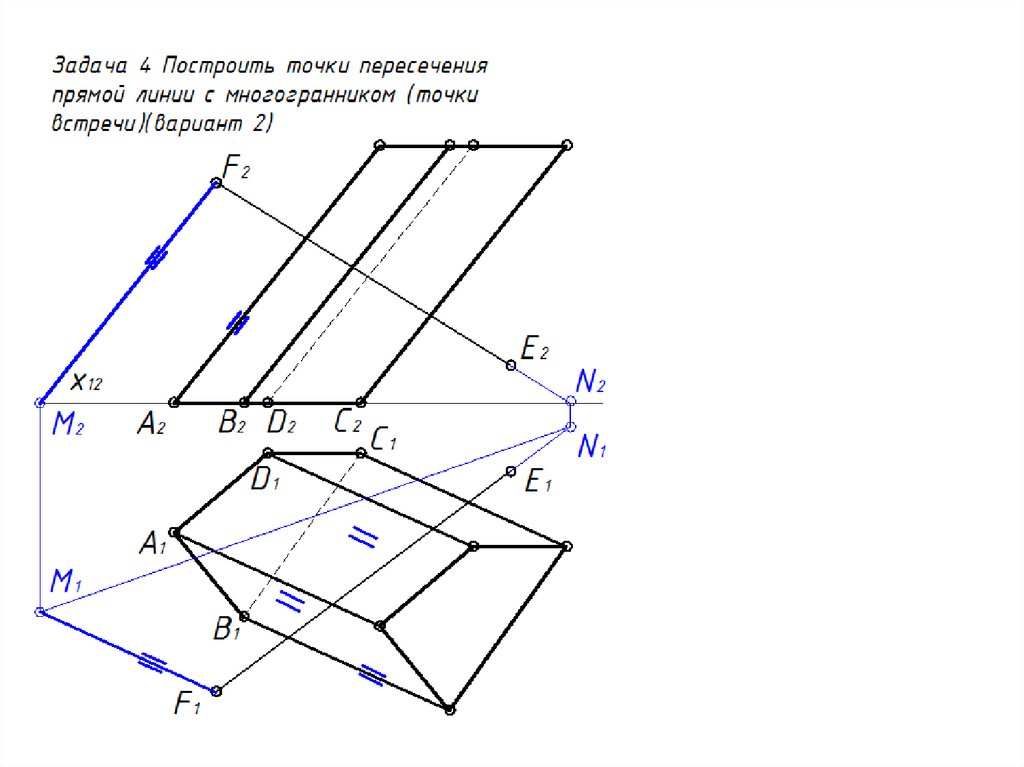
49. Пересечение многогранника прямой линией
Задача 4вариант 2





















































 Математика
Математика








