Похожие презентации:
Гамильтоновы цепи в некоторых типах линейно-выпуклых графов
1. МИНОБРНАУКИ РОССИИ «Челябинский государственный университет» Математический факультет Кафедра теории управления и оптимизации
Выпускная квалификационная работаГамильтоновы цепи в некоторых
типах линейно-выпуклых графов
Выполнил студент Лузин В.О.
Академическая группа МП-401
Научный руководитель Белов Е.Г.
Доцент, кандидат физикоматематических наук
2. Актуальность темы
Актуальность теории графов в различных отраслях наук1. В информатике – граф-схема алгоритма, кодирование и
декодирование информации
2. В физике – при построении электрических схем
3. В геометрии – чертежи многоугольников
многогранников, пространственных фигур
4. В экономике – при решении задач о выборе
оптимального пути для потоков грузового транспорта
(схем авиалиний, метро, железных дорог)
5. В географии – при составлении карт
3. Гамильтоновы цепи и циклы
Задача коммивояжера заключается в отыскании самоговыгодного маршрута, проходящего через указанные
города хотя бы по одному разу с
последующим возвратом в исходный город
Гамильтонов цикл Гамильтонова цепь незамкнутая задача коммивояжера
замкнутая задача
коммивояжера
4. Линейно-выпуклые эллипсы
•Теорема1. Если 2a > 2x + y ,где
-четное, -нечетное, то в линейновыпуклом эллипсе не существует
гамильтоновой цепи
5. Линейно-выпуклые эллипсы
теоремы 1• Доказательство
1. Локальное рассогласование четности
Шаг 1.
Граничное сечение эллипса
Шаг 2.
6. Линейно-выпуклые эллипсы
Аналогично
можно построить
гамильтоновы цепи в линейных эллипсах
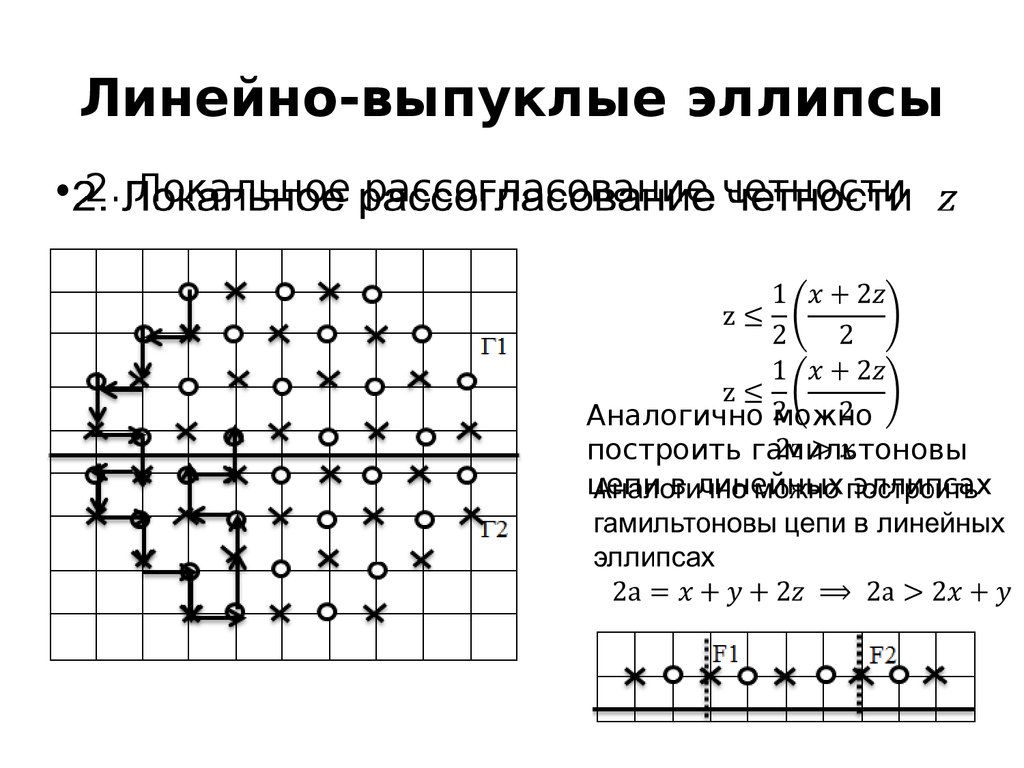
7. Линейно-выпуклые эллипсы
• 2.Локальное рассогласование четности
Аналогично можно
построить гамильтоновы
цепи в линейных эллипсах
8. Склейки прямоугольных графов
Инцидентные вершины в склейкепрямоугольных графов
Расстояние
пар точек по линейной норме равно
•
единице, т.е. или
9.
Склейки прямоугольныхграфов
•Теорема
2. Если в прямоугольных
графах и существуют гамильтоновы
циклы, то в склейке существует
гамильтонов цикл.
цикл в
поворот ребер
10. Склейки прямоугольных графов
Теорема 3. Если в любомпрямоугольном графе четное число
вершин, то в нем существует
гамильтонов цикл.
граф n×2k
граф 2k×m
11. Склейки прямоугольных графов
4. Если в существует•Теорема
гамильтонов цикл, а в существует
гамильтонова цепь, то в склейке
существует гамильтонова цепь.
Цепь в склейке











 Математика
Математика Физика
Физика








