Похожие презентации:
Приближенное решение уравнений. Метод Ньютона (метод касательных). Лекция 6
1.
Приближенное решение уравнений.Метод Ньютона (метод касательных)
Пусть ξ – корень уравнения
f x и
Пусть
f x непрерывны и сохраняют определённые знаки при a x b
xn
Тогда
f x 0 отделён на отрезке [a, b], причём
- n – е приближение корня и
a xn b.
xn hn
(2)
Уточним корень по методу Ньютона. Применяя формулу Тейлора
0 f xn hn f x n hn f xn
получим
hn
f xn
f xn
Следовательно,
xn 1 xn
f xn
f xn
n 0,1, 2,
2.
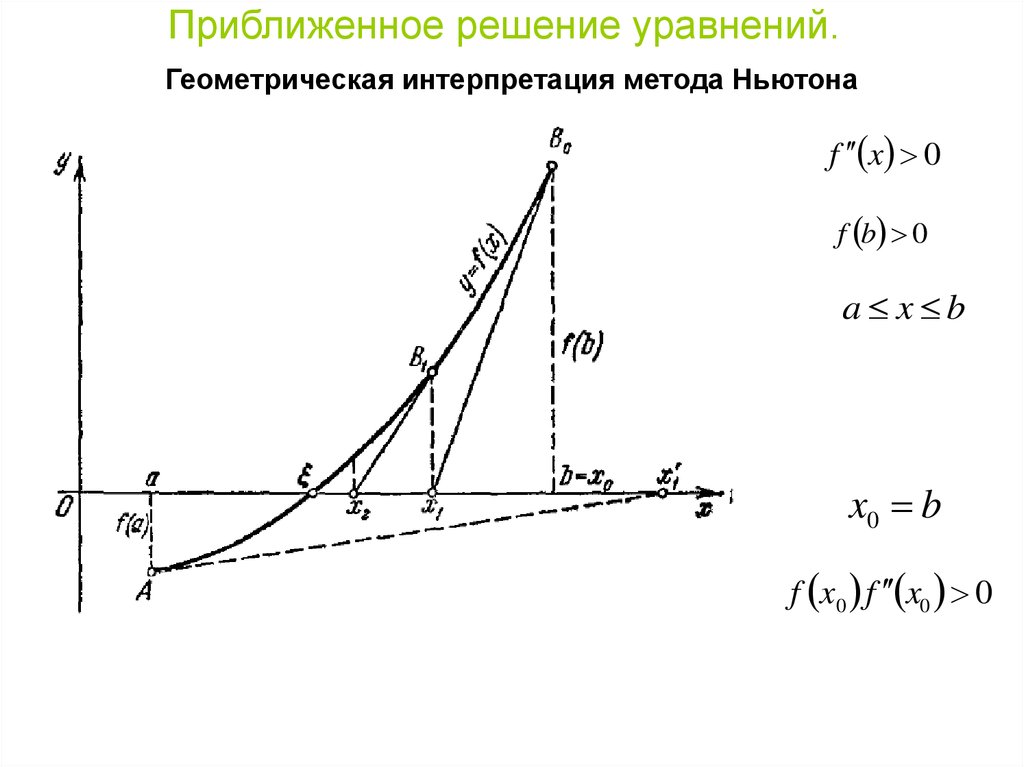
Приближенное решение уравнений.Геометрическая интерпретация метода Ньютона
f x 0
f b 0
a x b
x0 b
f x0 f x0 0
3.
Приближенное решение уравнений.Метод Ньютона
Доказательство.
Пусть f a 0 , f b 0, f x 0 , f x 0 при a x b .
Согласно неравенству f x0 f x0 0 ,
f x 0 0 . Тогда начальное
приближение можно выбрать как x0 b.
Докажем, что все xn (n = 1, 2, …) и, следовательно, f xn 0 .
Прежде всего x0 .
Предположим, что и xn .
Положим xn xn .
Применяя формулу Тейлора, получим:
1
2
,где сn
0 f f x n f xn xn f c n xn
2
xn
4.
Приближенное решение уравнений.Метод Ньютона
Так как f x 0 , то f x n f xn xn 0 .
Следовательно,
f xn
xn 1 xn
f xn
Таким образом показали, что все xn (n = 1, 2, …) и f xn 0 .
Так как f x 0 и f xn 0 , то xn 1 xn (n = 0, 1, 2, …)
Следовательно, приближения
x0 , x1, , xn ,
образуют ограниченную монотонно убывающую последовательность.
Следовательно, существует
lim xn
n
Перейдем к пределу в итерационной формуле м. Ньютона: f
f
То есть
f 0 следовательно, что и требовалось доказать.
5.
Приближенное решение уравнений.Метод Ньютона
Оценка точности
Вариант оценки 1 (общая формула).
x n
f xn
m1
, где
f x m1 при a x b
Вариант оценки 2.
xn
M2
xn xn 1 2
2m1
//вывод на доске
f x m1
f x M 2
6.
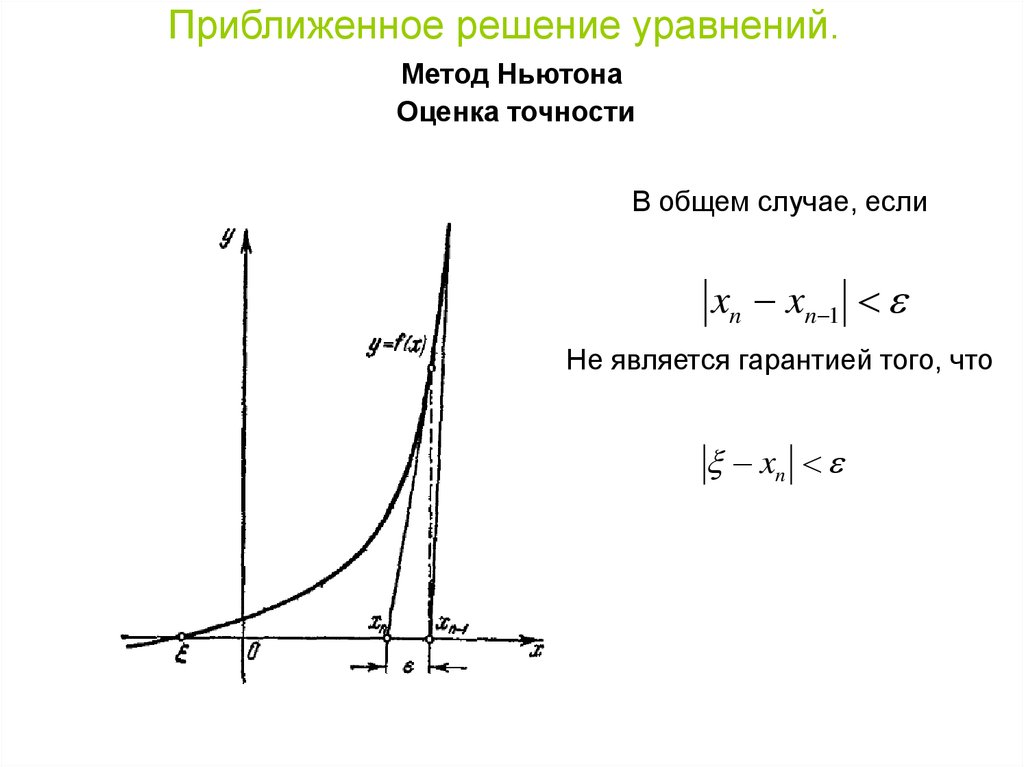
Приближенное решение уравнений.Метод Ньютона
Оценка точности
В общем случае, если
xn xn 1
Не является гарантией того, что
xn
7.
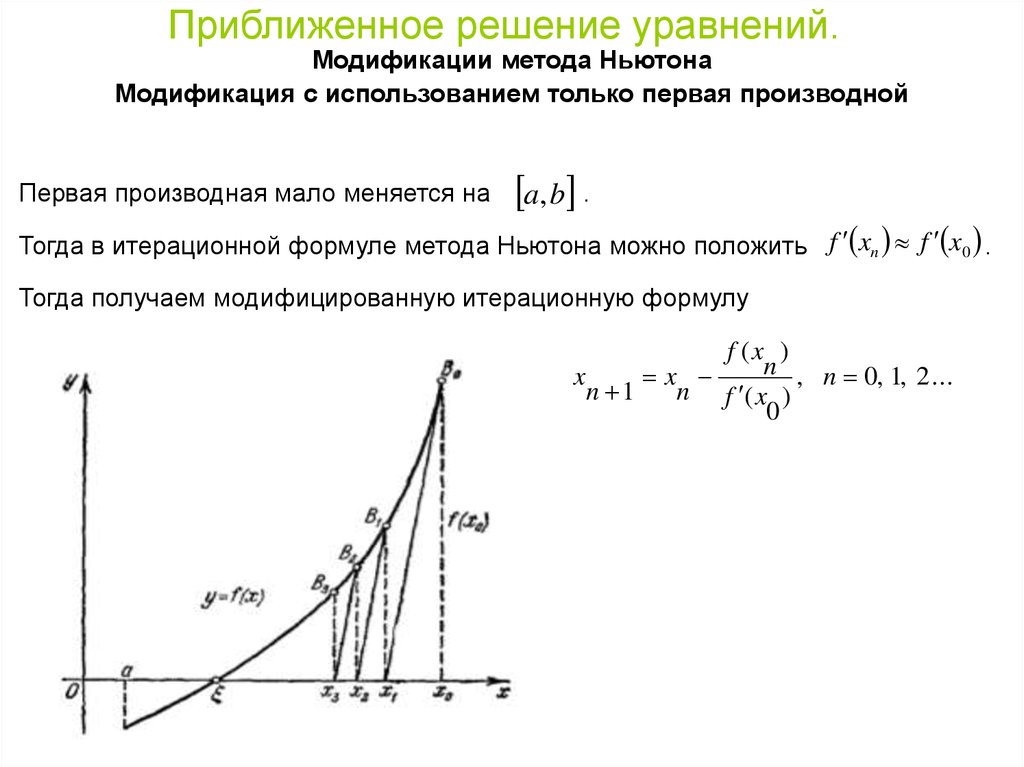
Приближенное решение уравнений.Модификации метода Ньютона
Модификация с использованием только первая производной
Первая производная мало меняется на
a, b .
Тогда в итерационной формуле метода Ньютона можно положить f xn f x0 .
Тогда получаем модифицированную итерационную формулу
f (x )
n , n 0, 1, 2 . . .
x
x
n 1
n f ( x )
0
8.
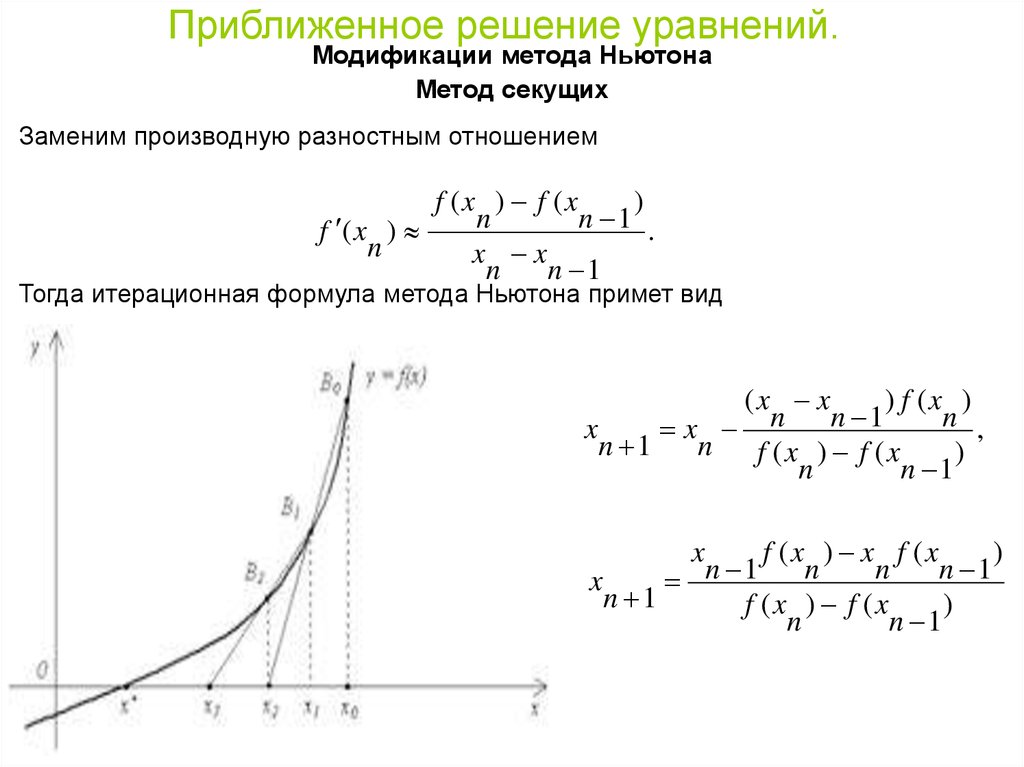
Приближенное решение уравнений.Модификации метода Ньютона
Метод секущих
Заменим производную разностным отношением
f (x ) f (x
)
n
n
1
f ( x )
.
n
x x
n
n 1
Тогда итерационная формула метода Ньютона примет вид
(x x
) f (x )
n
n
1
n ,
x
x
n 1
n f (x ) f (x
)
n
n 1
или
f (x ) x f (x
)
n
1
n
n
n
1
x
n 1
f (x ) f (x
)
n
n 1
x
9.
Приближенное решение уравнений.Метод простой итерации
f x 0
f x - непрерывная функция. Требуется найти вещественные корни.
Заменим уравнение f x 0 равносильным уравнением:
Выберем грубое приближенное значение корня
x x
x0
x1 x0
x2 x1
...........
xn xn 1
n 1, 2, ...
Если эта последовательность сходящаяся, то есть существует предел
lim xn
n
lim xn ( lim xn 1 )
n
n
10.
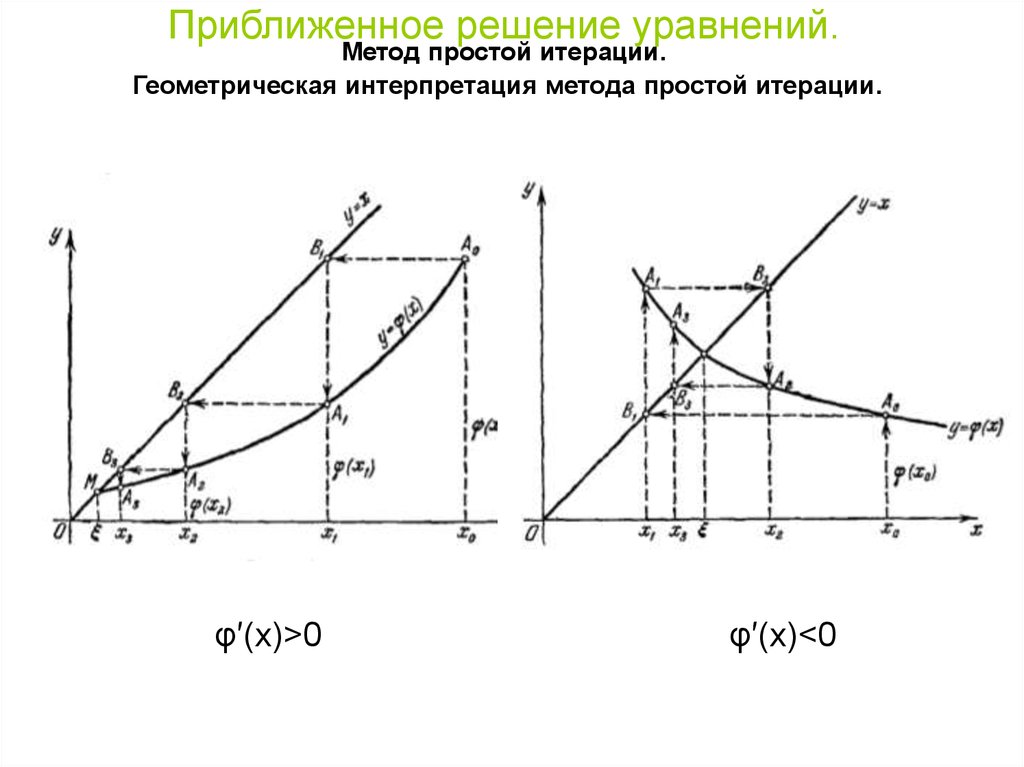
Приближенное решение уравнений.Метод простой итерации.
Геометрическая интерпретация метода простой итерации.
φ′(x)>0
φ′(x)<0
11.
Приближенное решение уравнений.Метод простой итерации.






 Математика
Математика








