Похожие презентации:
Закон сохранения момента импульса системы материальных точек
1. Закон сохранения момента импульса системы материальных точек
Момент силы и импульсаотносительно точки и оси
2. Статика – инженерная наука, изучающая равновесие твердых тел, находящихся под действием сил. Она необходима для определения
максимальнодопустимых
нагрузок.
• Чтобы удержать тело в покое (равновесии),
необходимо выполнение 2-х условий:
Fi 0
1. Векторная сумма всех сил равна 0
2. Векторная сумма всех моментов сил равна 0
Мi 0
3. Момент силы F относительно неподвижной точки 0 – физическая величина, определяемая векторным произведением радиус-вектора r,
проведенного из точки 0 в точку приложенияM
M r F sin ,
r sin l плечо силы.
F
r
0
l
α
M M xi M y j M z k ,
r
M r F ,
M псевдовектор.
силы, на силу F.
Mx r F ,M y r F ,Mz r F .
x
y
z
4.
zF
M
z
M
r
0
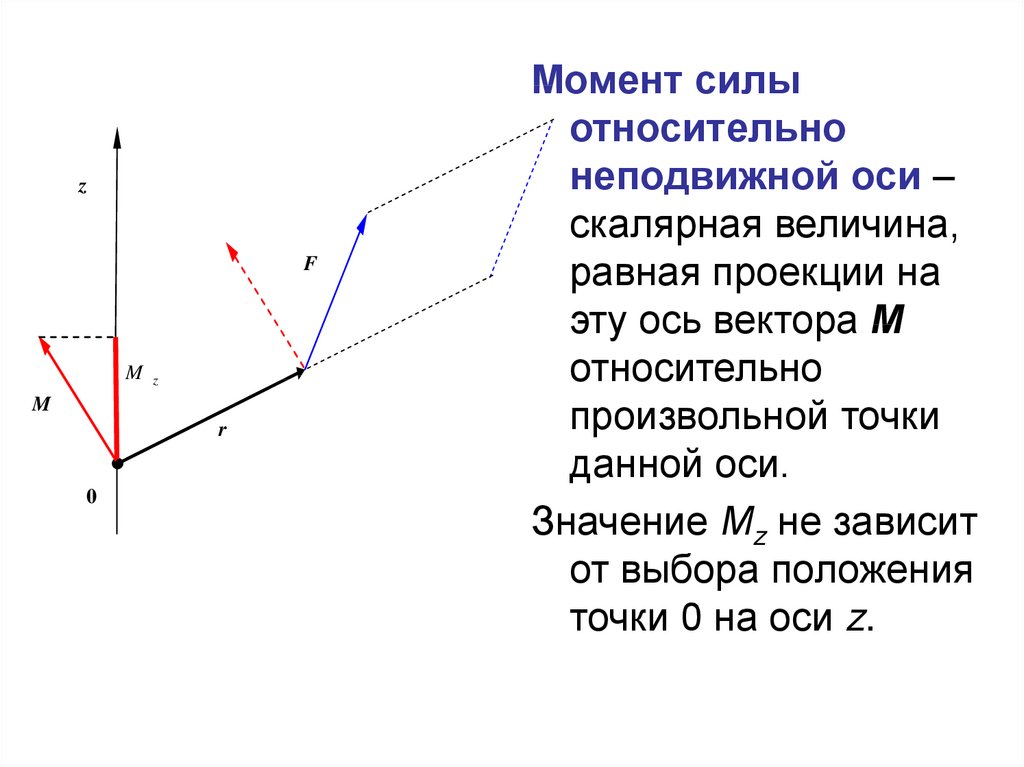
Момент силы
относительно
неподвижной оси –
скалярная величина,
равная проекции на
эту ось вектора М
относительно
произвольной точки
данной оси.
Значение Мz не зависит
от выбора положения
точки 0 на оси z.
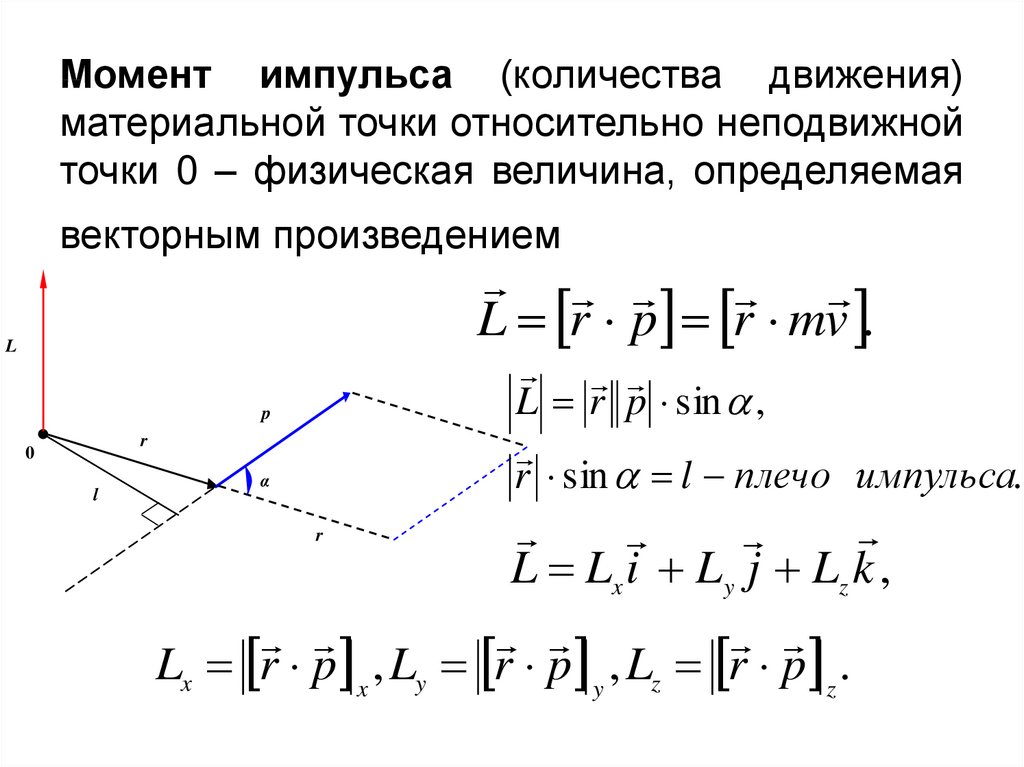
5. Момент импульса (количества движения) материальной точки относительно неподвижной точки 0 – физическая величина, определяемая
векторным произведениемL r p r mv .
L
L r p sin ,
r sin l плечо импульса.
p
r
0
l
α
L Lx i Ly j Lz k ,
Lx r p x , Ly r p y , Lz r p z .
r
6. Момент импульса относительно неподвижной оси – скалярная величина, равная проекции на эту ось вектора L относительно
произвольной точки данной оси.L r p .
L
v
Для движения по
окружности:
L R mv .
R
2
L Rmvsin v
, R Rm v mR .
R
v R
7. Уравнение моментов
dLM.
dt
Математическая справка: d x y dx y x dy .
dt
dt
dt
d dr dp
r p
p r
dt dt
dt
L
v
F
dL
dL
v p
r
F
M.
dt 0
dt
M
,v p
sin v , p 0
L M
8. Производная по времени от момента импульса относительно точки равна моменту силы относительно этой точки.
dL Производная по времени отM . момента импульса относительно
dt
точки
равна
моменту
силы
относительно этой точки.
Производная по времени от момента
импульса относительно оси равна
моменту силы относительно этой оси.
dLy
dLx
dLz
Mx,
My,
Mz.
dt
dt
dt
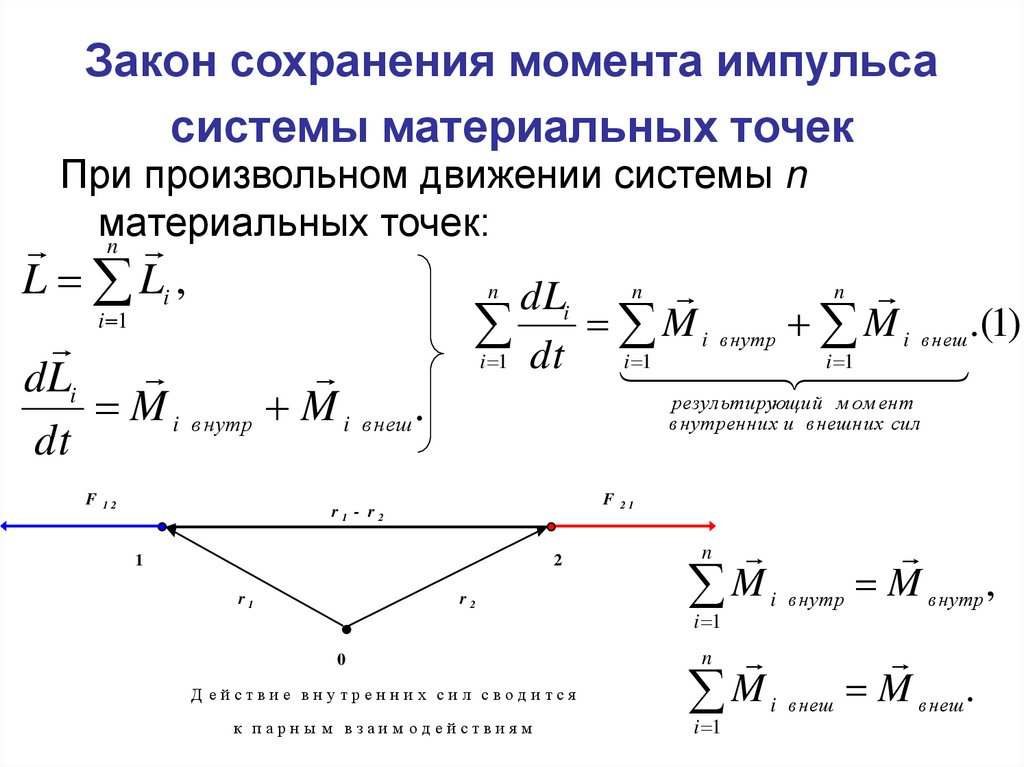
9. Закон сохранения момента импульса системы материальных точек
При произвольном движении системы nматериальных
точек:
n
L Li ,
n
n
n
dL
i
i 1
M i внутр M i внеш .(1)
i 1 dt
i 1
i 1
dLi
M i в нутр M i в неш .
dt
F
12
результирующий м ом ент
внутренних и внешних сил
F
r1 - r2
1
2
r1
r2
0
Д ей стви е вн утрен н и х си л своди тся
к п ар н ы м в заи м о д ей стви я м
21
M i в нутр M в нутр ,
n
i 1
M i в неш M в неш.
n
i 1
10.
M 1 r1 F12 , M 2 r2 F21 ,M 2 r2 F12
3 з н. Ньютона : F12 F21.
M 1 M 2 r1 r2 F12 r F12 0,
т.к. r F12 , r , F12 0.
Результирующий момент внутренних сил
в соответствии с третьим законом
Ньютона равен нулю.
11. В уравнении (1) операции дифференцирования и суммирования можно поменять местами:
nn
dLi
M i внутр M i внеш .(1)
i 1 dt
i 1
i 1
n
результирующий м ом ент
внутренних и внешних сил
В
уравнении
(1)
операции
дифференцирования и суммирования
n
d
d
L
можно поменять местами:
Li
M внеш.
dt i 1
dt
Если внешние силы на систему не действуют,
то
dL
М внеш 0
0 L const.
dt
Момент импульса замкнутой системы величина
постоянная, т.е. с течением времени не
меняется – закон сохранения момента
импульса.
12.
Закон сохранения момента импульсаявляется прямым следствием законов
Ньютона и изотропности пространства –
эквивалентности свойств пространства
в различных направлениях.
Во многих задачах, связанных с
вращающимися системами, угловая
скорость вращения ω и момент
импульса можно вычислить с помощью
закона сохранения момента импульса.
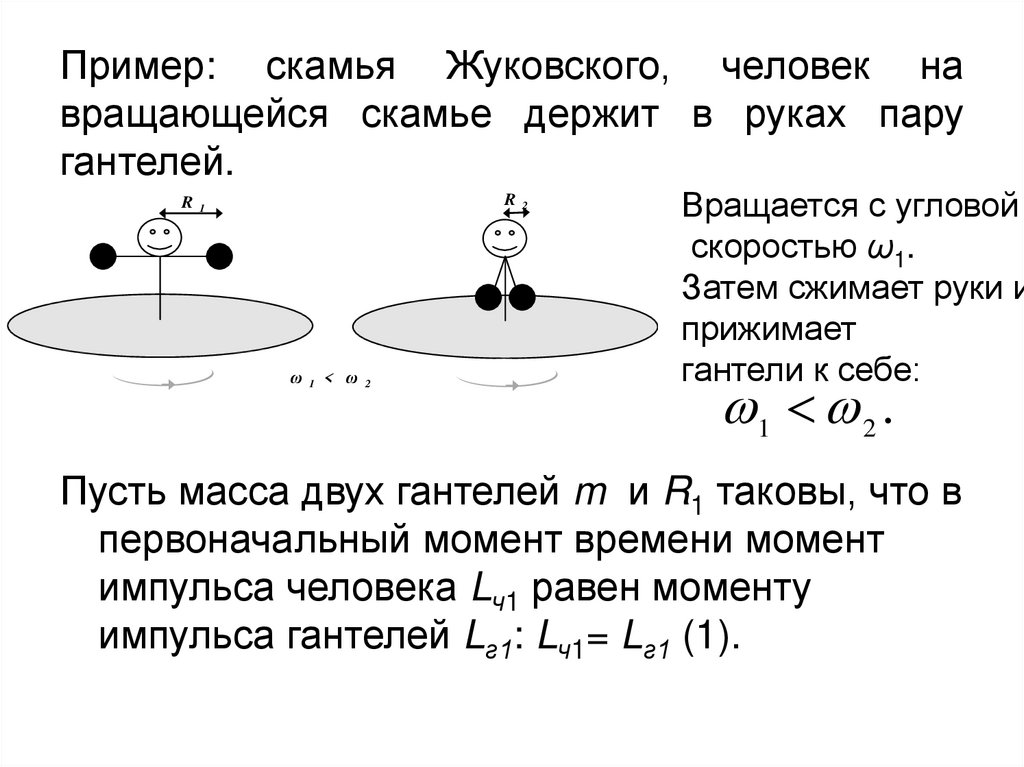
13. Пример: скамья Жуковского, человек на вращающейся скамье держит в руках пару гантелей.
RR
1
ω
1
< ω
2
2
Вращается с угловой
скоростью ω1.
Затем сжимает руки и
прижимает
гантели к себе:
1 2 .
Пусть масса двух гантелей m и R1 таковы, что в
первоначальный момент времени момент
импульса человека Lч1 равен моменту
импульса гантелей Lг1: Lч1= Lг1 (1).
14.
Lг1 R1mv1 R1m 1 R1 m 1 R .(2)2
1
Начальный момент импульса системы:
L1 Lч1 m 1 R .(3)
2
1
Т.к. Lч1= Lг1
Lч1 m 1 R .(4)
2
1
L2 Lч 2 m 2 R .(5)
2
2
Во втором случае:
По закону сохранения момента импульса
(уравнение (3) равно (5)):
Lч 2 m 2 R Lч1 m 1 R .(6)
2
2
2
1
15.
Lч1 mч 1r , (7)2
Уравнение (7) делим на (8):
Lч 2 mч 2 r .(8)
Lч1 1
2
Lч 2 Lч1 .(9)
Lч 2 2
1
2
Уравнение (9) подставляем в (6):
2
2
2
Lч1
m 2 R2 Lч1 m 1 R1 .(10)
1
Уравнение (4) подставляем в (10):
2
2
2
m 1 R
1 m 1 R1 2 R2 ,
1
2
1
16.
22
2
m 1 R
1 m 1 R1 2 R2 ,
1
2
1
2 R 1 R 1 R 2 R ,
2
1
2
1
2
1
2
2
R
2 R R 2 1 R , 2 2 1 2
;
2
R1 R2
2
1
2
2
2
1
2
1
R2 R1 2 2 1.
Аналогичная ситуация возникает,
когда фигурист прижимает руки к себе
и начинает вращаться быстрее.
17. Гироскоп
• Гироскоп – быстро вращающеесясимметричное твердое тело, ось
вращения которого может изменять
свое направление в пространстве.
Происходит от греческого гиро скоп
наблюдаю
кружусь
18. Свойства гироскопа проявляются у вращающихся небесных тел, снаряда (пули), роторов турбин, установленных на судах, волчка, юлы.
На свойствах гироскопа основаны различныеприборы и устройства, применяемые в
технике.
Свойства гироскопа проявляются при
выполнении двух условий:
1. ось вращения гироскопа должна иметь
возможность изменять своё положение в
пространстве;
2. частота вращения гироскопа вокруг своей оси
должна быть много больше скорости
изменения направления оси в пространстве.
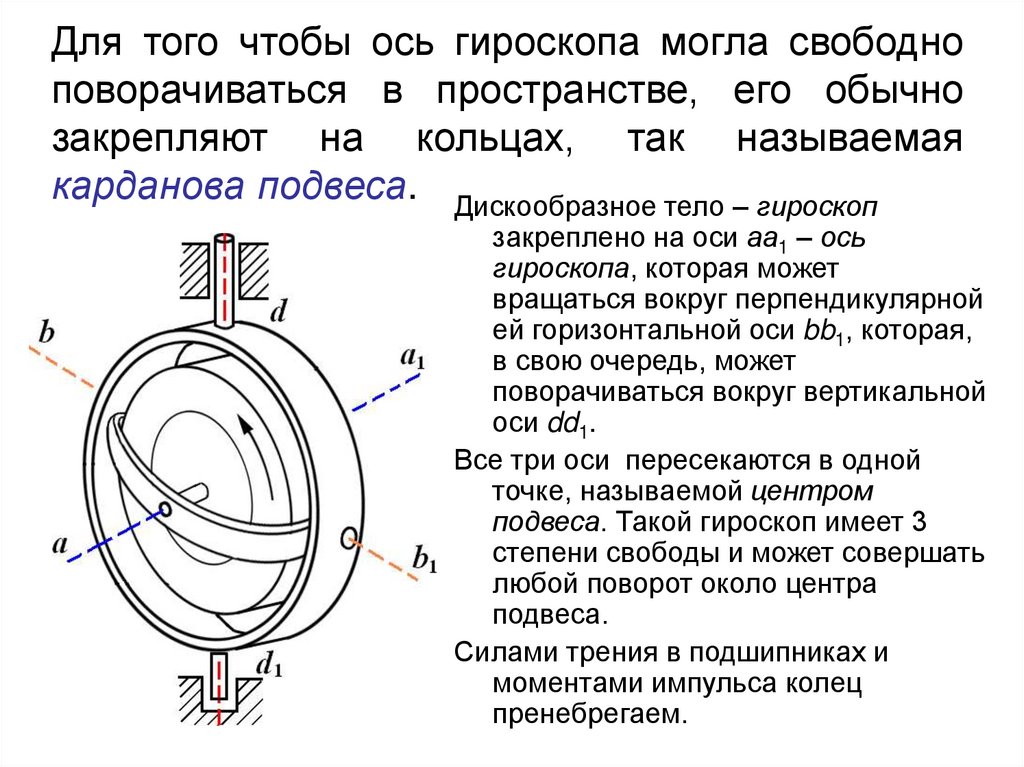
19. Для того чтобы ось гироскопа могла свободно поворачиваться в пространстве, его обычно закрепляют на кольцах, так называемая
карданова подвеса. Дискообразное тело – гироскопзакреплено на оси аа1 – ось
гироскопа, которая может
вращаться вокруг перпендикулярной
ей горизонтальной оси bb1, которая,
в свою очередь, может
поворачиваться вокруг вертикальной
оси dd1.
Все три оси пересекаются в одной
точке, называемой центром
подвеса. Такой гироскоп имеет 3
степени свободы и может совершать
любой поворот около центра
подвеса.
Силами трения в подшипниках и
моментами импульса колец
пренебрегаем.
20.
Пока гироскоп неподвижен, его можноориентировать в пространстве любым
образом.
Если гироскоп начинает вращаться с большой
угловой скоростью ω, то при отсутствии
внешних сил (Fвнеш =0) М = 0 и т.е. ось
гироскопа сохраняет свое положение в
пространстве.
21.
yF
dL
L
L′
M
p
z
F
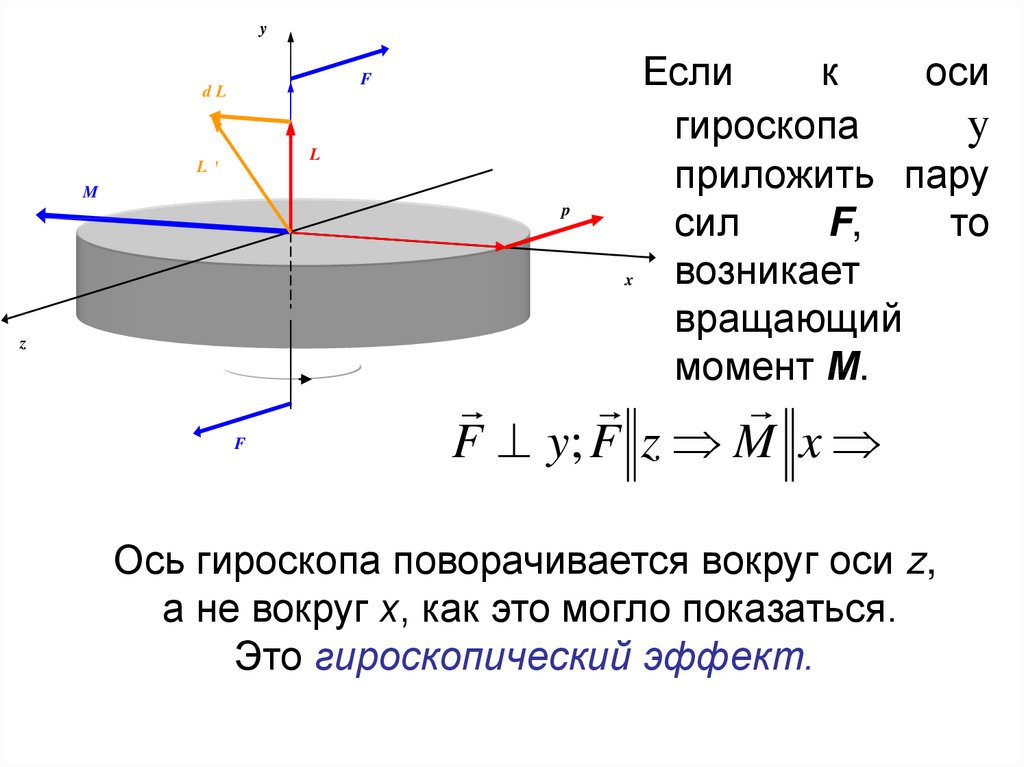
Если
к
оси
гироскопа
y
приложить пару
сил
F,
то
возникает
x
вращающий
момент М.
F y; F z M x
Ось гироскопа поворачивается вокруг оси z,
а не вокруг х, как это могло показаться.
Это гироскопический эффект.
22.
yF
dL
L
L′
M
p
x
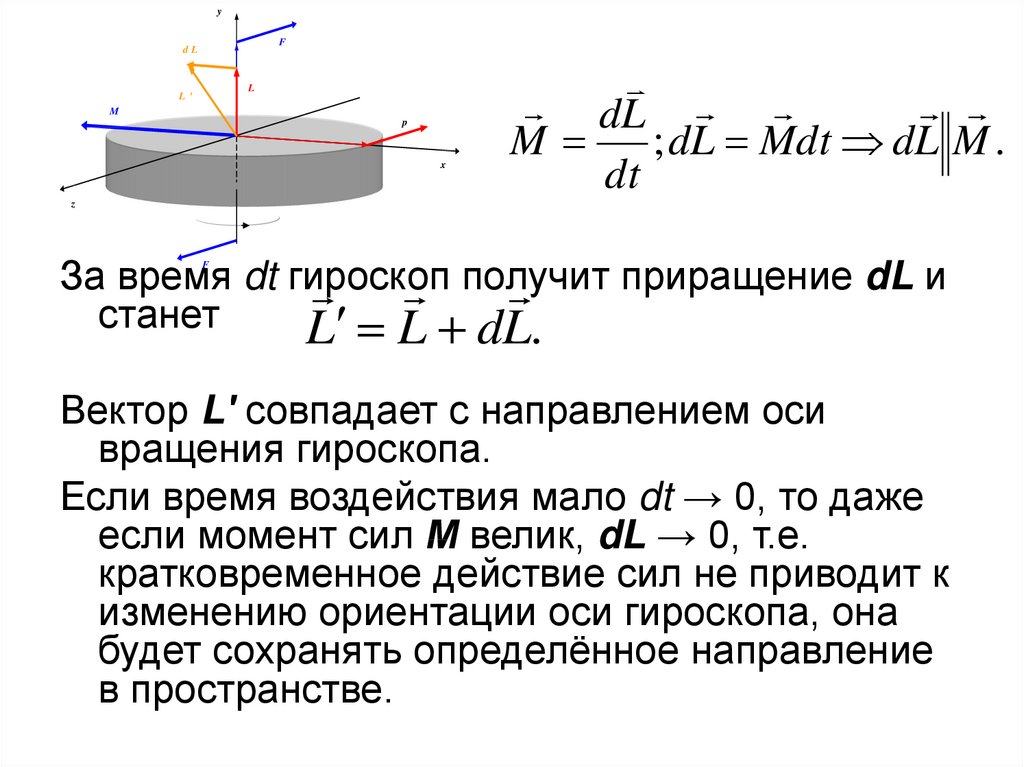
dL
M
; dL Mdt dL M .
dt
z
За время dt гироскоп
приращение dL и
получит
станет
L L dL.
F
Вектор L′ совпадает с направлением оси
вращения гироскопа.
Если время воздействия мало dt → 0, то даже
если момент сил М велик, dL → 0, т.е.
кратковременное действие сил не приводит к
изменению ориентации оси гироскопа, она
будет сохранять определённое направление
в пространстве.
23. Гироскоп
Применение:- навигационные устройства (гирокомпас,
гирогоризонт),
- поддержание заданного направления
движения (автопилот).
При конструировании судов и самолетов
необходимо учитывать гироскопические
силы, возникающие в подшипниках
массивных валов двигателей, роторов
турбин, гребных валов и т.п.
24. Динамика вращательного движения абсолютно твёрдого тела относительно неподвижной оси
Основное уравнениединамики вращательного
движения
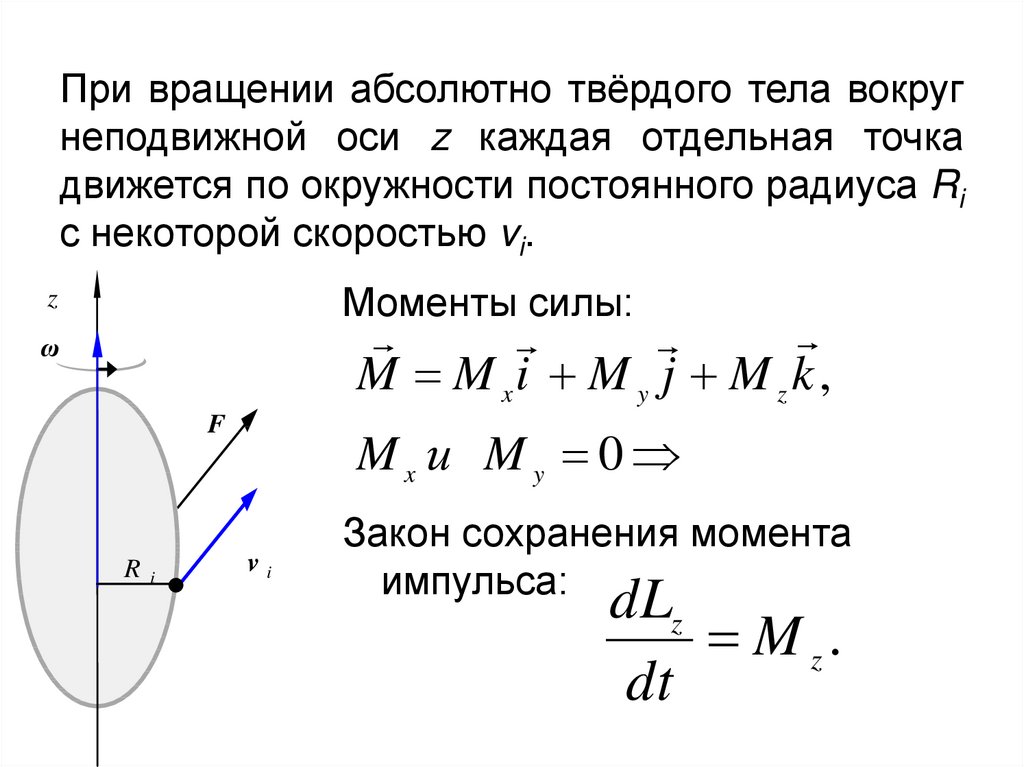
25. При вращении абсолютно твёрдого тела вокруг неподвижной оси z каждая отдельная точка движется по окружности постоянного радиуса
Riс некоторой скоростью vi.
Моменты силы:
z
M M xi M y j M z k ,
ω
F
R
i
Mx и My 0
vi
Закон сохранения момента
импульса:
dLz
M z.
dt
26.
Момент импульсаотносительно точки 0 для i
точки твёрдого тела:
z
ω
vi
R
ai
0
i
ri
Li ri mi vi ai Ri mi vi .
Проекция на ось z
Li относительно точки 0:
Li ai Ri mi vi
z
z
ai mi vi z Ri mi vi .
z
27.
ai mi vi z 0 т.к. ai mi vi z.z
ai mi vi
vi
ai
z
Ri mi vi
Ri mi vi
vi
R
i
z
Li .
z
Liz Ri mi vi ,
vi Ri . Liz mi R .
2
i
28. Твёрдое тело – система жёстко связанных материальных точек.
Твёрдоетело
–
система
связанных материальных точек.
жёстко
Следовательно, для твёрдого тела:
n
n
n
Lz Liz mi R mi R .
i 1
i 1
J i mi R
2
i
2
i
i 1
2
i
- момент инерции
материальной точки относительно оси z.
n
2
J z mi Ri - момент инерции твердого тела
i 1 относительно оси z.
n
Lz Liz - момент импульса (количества
i 1
движения) твердого тела
относительно оси z.
29.
L z J z .dLz
M z.
Закон сохранения момента импульса:
dt
d J z
d
Jz
Jz M z.
dt
dt
Т.к. координатную ось z приняли
произвольно, индекс можно опустить.
M J – основное уравнение динамики
вращательного движения.
30. В общем случае:
MJ
– ускорение вращения твердого тела
относительно неподвижной оси прямо
пропорционально моменту всех внешних сил
относительно этой оси и обратно
пропорционально моменту инерции твердого
тела относительно этой оси.
• Физический смысл:
Момент инерции относительно оси – мера
инерции твердого тела при вращательном
движении относительно оси.
31. Момент инерции. Теорема Гюйгенса-Штейнера
Момент инерции системы тел –физическая величина равная сумме
2
ri :
произведений mi на
J mi ri .
2
В случае непрерывного распределения
масс сумма сводится к интегралу:
J r dm r dV .
2
m
2
V
32.
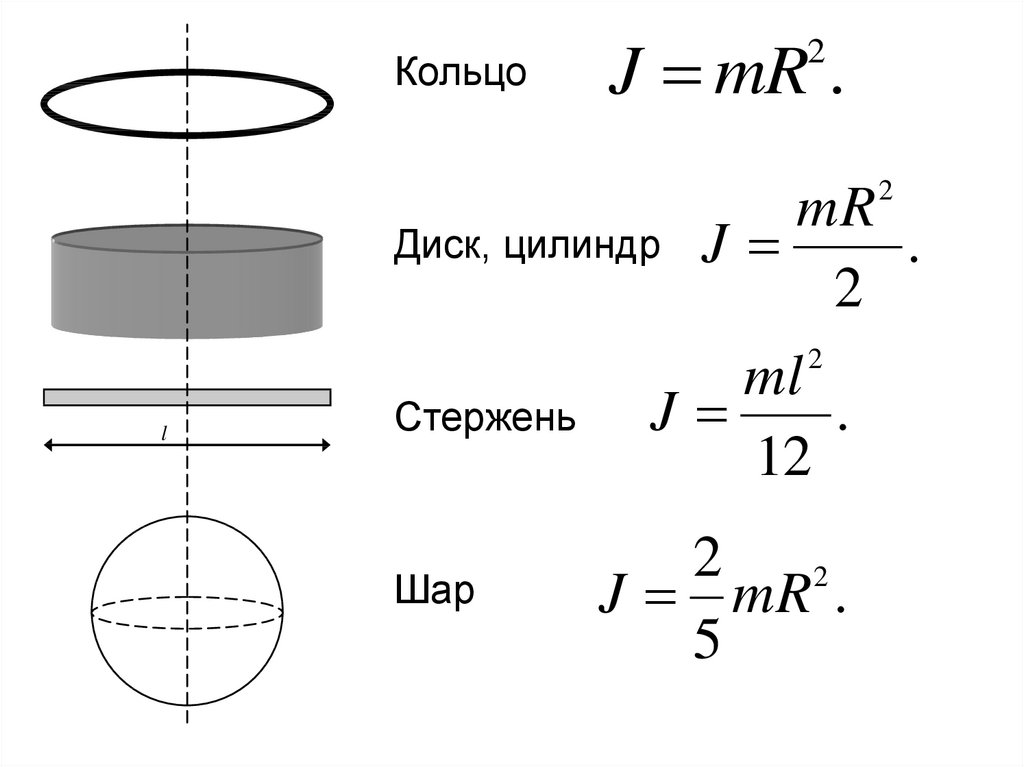
КольцоJ mR .
2
2
Диск, цилиндр
mR
J
.
2
2
l
Стержень
Шар
ml
J
.
12
2
2
J mR .
5
33.
Теорема Гюйгенса-Штейнера: моментинерции относительно произвольной оси
равен моменту инерции относительно
параллельной ей оси, проходящей через
центр масс J0, сложенному с
произведением массы тела на квадрат
расстояния между ними а2.
J J 0 ma .
2
a
l
2
ml
l 1 2
J J 0 ma
m ml .
12
2 3
2
2
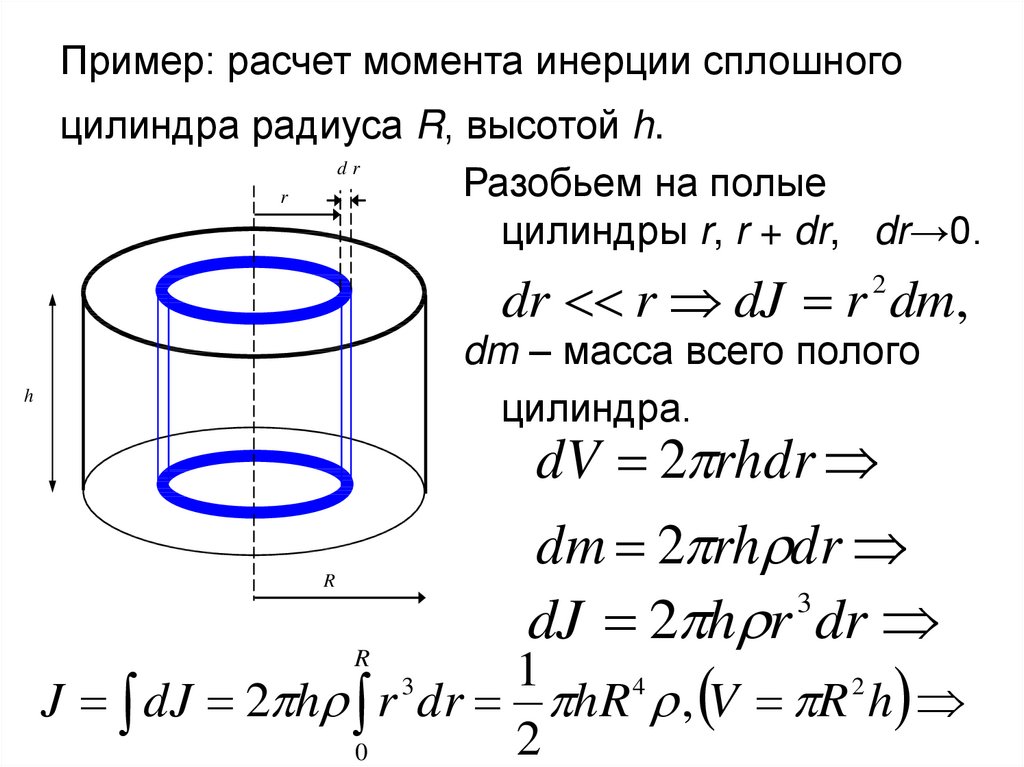
34. Пример: расчет момента инерции сплошного цилиндра радиуса R, высотой h.
drРазобьем на полые
r
цилиндры r, r + dr, dr→0.
dr r dJ r dm,
2
dm – масса всего полого
цилиндра.
h
dV 2 rhdr
dm 2 rh dr
3
dJ 2 h r dr
R
1
4
2
J dJ 2 h r dr hR , V R h
2
0
R
3
35.
14
2
J dJ 2 h r dr hR , V R h
2
0
R
3
dr
2
r
mR
J
.
2
h
R
36. Закон сохранения момента импульса АТТ относительно неподвижной оси
В общем видеdL
M.
dt
В замкнутой системе М 0.
dL
0,
dt
L const.
Фундаментальный закон, связан с
симметрией пространства, его
изотропностью, т.е. физические законы
не зависят от выбора направления осей
системы координат.
37. Скамья Жуковского.
L J const.J
0
2mR 1 J 0 2 const 1 2 .
2
1
R2 0.
R
R
1
ω
1
< ω
2
2
38. Кинетическая энергия при вращательном движении АТТ
Т.к. имеется АТТ, следовательно, для всехmi ω = const.
mi v
mi 2 2
J
2
Ек
Ri mi Ri
.
2
2
2
i 1
i 1 2
i 1
n
2
i
n
2
2
n
J
39. Динамика вращательного движения. Работа и мощность при вращательном движении относительно неподвижной оси
Основное уравнение динамикивращательного движения:
M
d
; M J
.(1)
J
dt
Закон сохранения момента импульса:
L J const.
Кинетическая энергия при вращательном
2
движении:
J
Ек
2
.(2)
40. Работа при вращательном движении идёт на увеличение его кинетической энергии:
dA dE к .(3)2
J
dA d
J d .(4)
2
Из (1) следует
Jd Mdt.(5)
Уравнение (5) подставляем в (4):
dA Mdt Md .(6) A M .(7)
41.
Мощность:dA
d
N
M
M .(8)
dt
dt
42. Плоское движение твердого тела
Плоское движение – движение, прикотором все участки траектории любых
двух точек твёрдого тела лежат в
параллельных плоскостях.
Кинетическая энергия складывается из
энергии поступательного движения и
2
2
энергии вращения.
mvc J c
Ек
,
2
2
vc – скорость центра масс,
Jc – момент инерции относительно оси,
проходящей через центр масс.
43. Поступательное движение Вращательное движение
rm
dr
v
dt
p m v
dp
F
dt
F
a
m
2
Ек
mv
2
A FS; N Fv
J
d
dt
L J
dL
M
dt
M
J
2
Ек
J
2
A M ;
N M










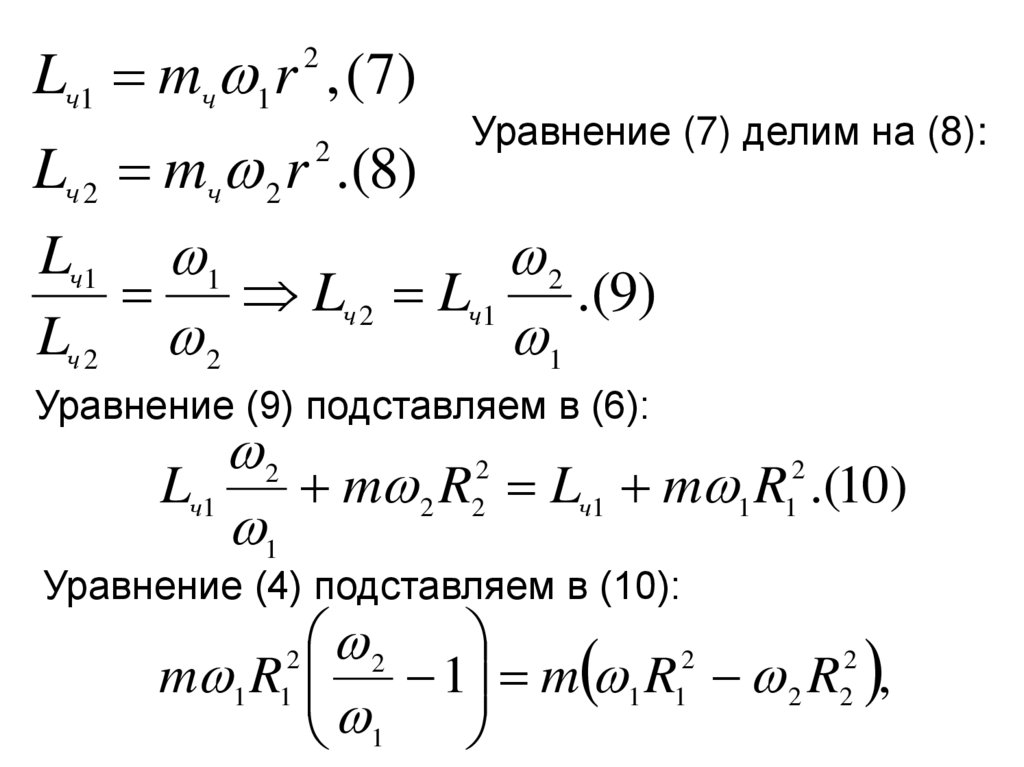






















 Физика
Физика








