Похожие презентации:
Механика твердого тела. Динамика вращений
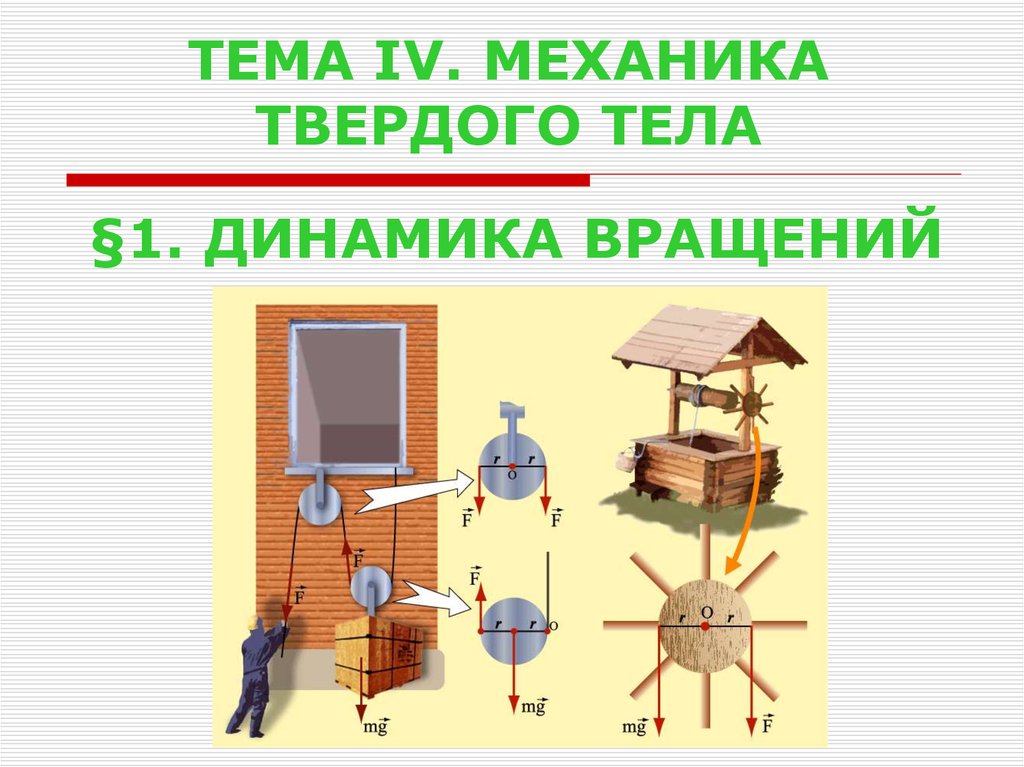
1. ТЕМА IV. МЕХАНИКА ТВЕРДОГО ТЕЛА
§1. ДИНАМИКА ВРАЩЕНИЙ2. 1. ДВИЖЕНИЕ ЦЕНТРА МАСС ТВЕРДОГО ТЕЛА
Центр масс твердого тела движется так, как двигалась быматериальная точка с массой, равной массе тела, под
действием всех приложенных к телу (внешних) сил.
N
N
N
i 1
i i
N
i 1
m a F . m r r m
i 1
i i
N
i 1
i
i 1
m r mr
N
i 1
mV
i 1
i i
i i
c
N
N
m a f F . f
mi ai fi Fi ;
N
N
i i
c
N
i 1
i
i
mrc .
mV
i i mVc .
i 1
N
mVc mac Fi .
i 1
i 1
i
i 1
i
0
3. 2.МОМЕНТ ИМПУЛЬСА
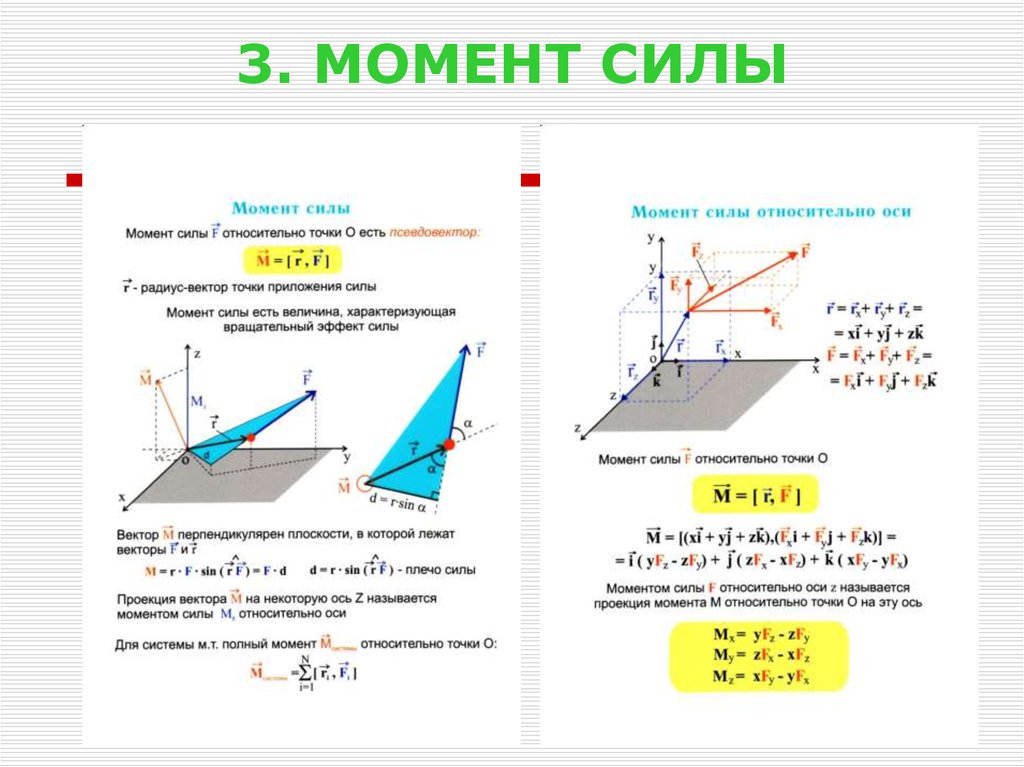
4. 3. МОМЕНТ СИЛЫ
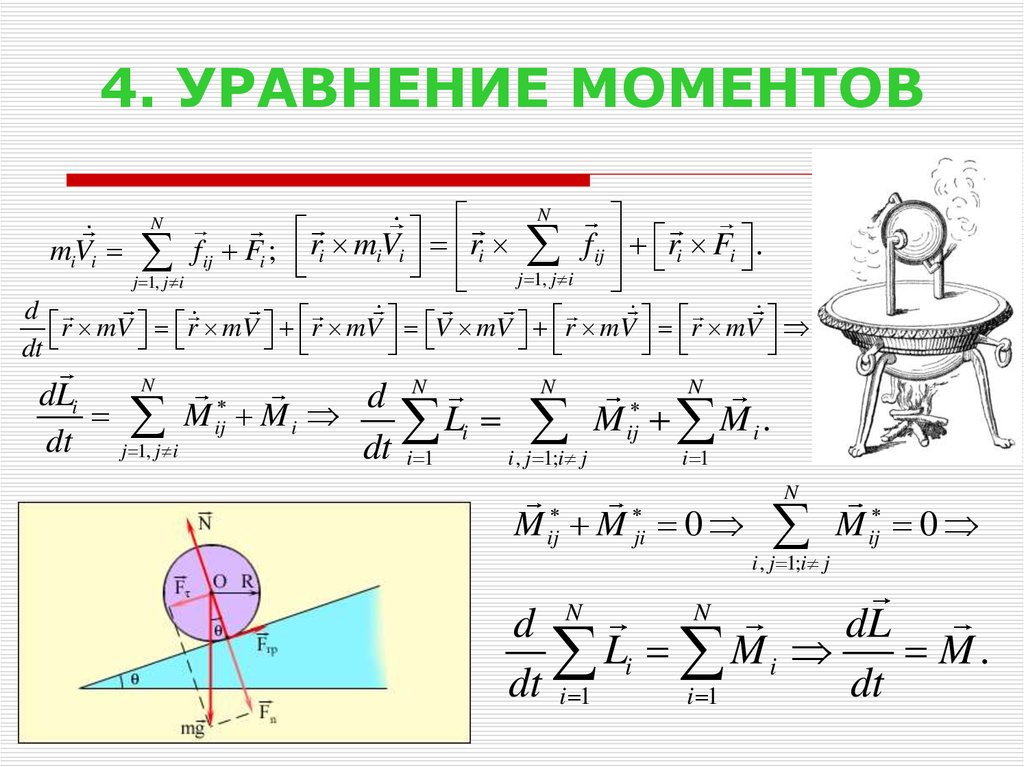
5. 4. УРАВНЕНИЕ МОМЕНТОВ
Nr mV
mV
i i ri f ij ri Fi .
i i f ij Fi ; i
j 1, j i
j 1, j i
N
d
r mV r mV r mV V mV r mV r mV
dt
dLi
dt
N
N
N
d N
M Mi
Li M ij M i .
j 1, j i
dt i 1
i , j 1;i j
i 1
ij
M ij M ji 0
N
i , j 1;i j
M ij 0
N
d N
dL
Li M i
M.
dt i 1
dt
i 1
6. 5. СУММАРНЫЙ МОМЕНТ ВНУТРЕННИХ СИЛ
7. 6. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
dL Mdt;M 0 dL 0 L const.
Момент импульса замкнутой
(изолированной) системы есть
величина постоянная.
M 0;
Mz 0
L const;
Lz const.
8. 7. МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛА
Li ri mVi i mi ri Vi .
ri Vi Li mi rV
i i ; Vi Ri
Lzi Li cos i mi ri Ri sin i ;
ri sin i Ri Lzi mi R z .
2
i
N
N
N
Lz Lzi mi R z z mi R ; I
i 1
i 1
2
i
i 1
2
i
N
m R
i 1
i
2
i
Lz I z .
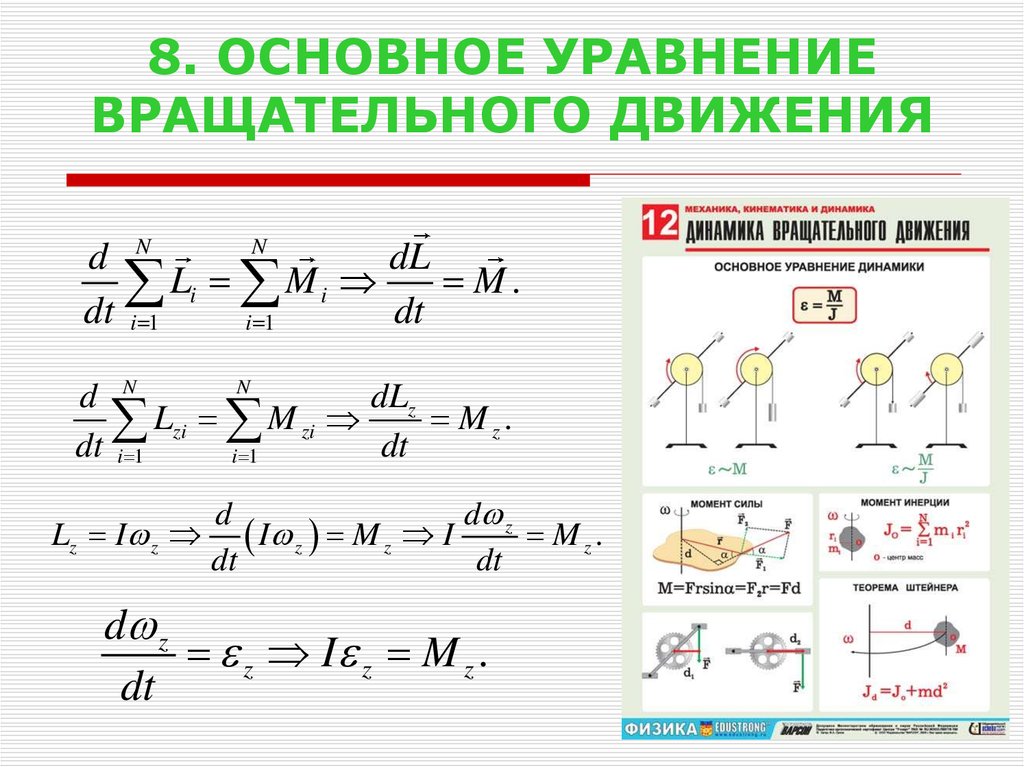
9. 8. ОСНОВНОЕ УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Nd N
dL
Li M i
M.
dt i 1
dt
i 1
N
d N
dLz
Lzi M zi
M z.
dt i 1
dt
i 1
Lz I z
d
d z
I
M
I
M z.
z
z
dt
dt
d z
z I z M z .
dt
10. 9. МОМЕНТ ИМПУЛЬСА И МОМЕНТ ИНЕРЦИИ
В общем случае L и несовпадают по направлению.
Для однородного тела,
симметричного относительно
оси вращения L I .
M 0 L I const.
M z 0 Lz I z const.
I1 z1 I 2 z 2 const;
I1 1 I1 I 2 .
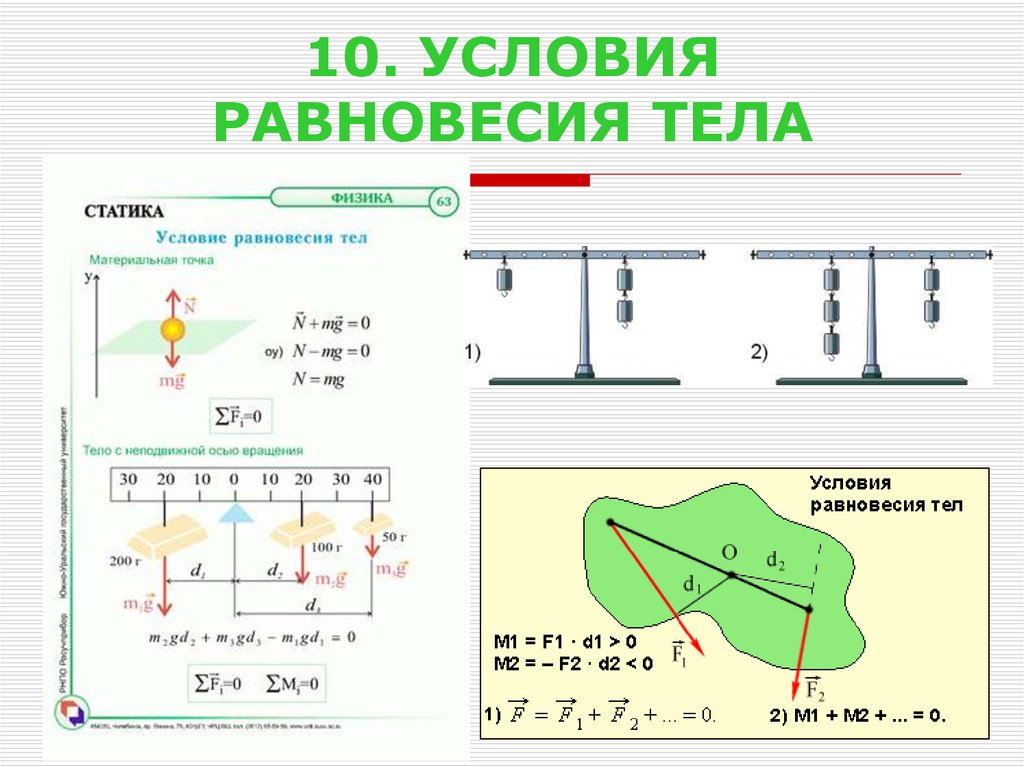
11. 10. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛА
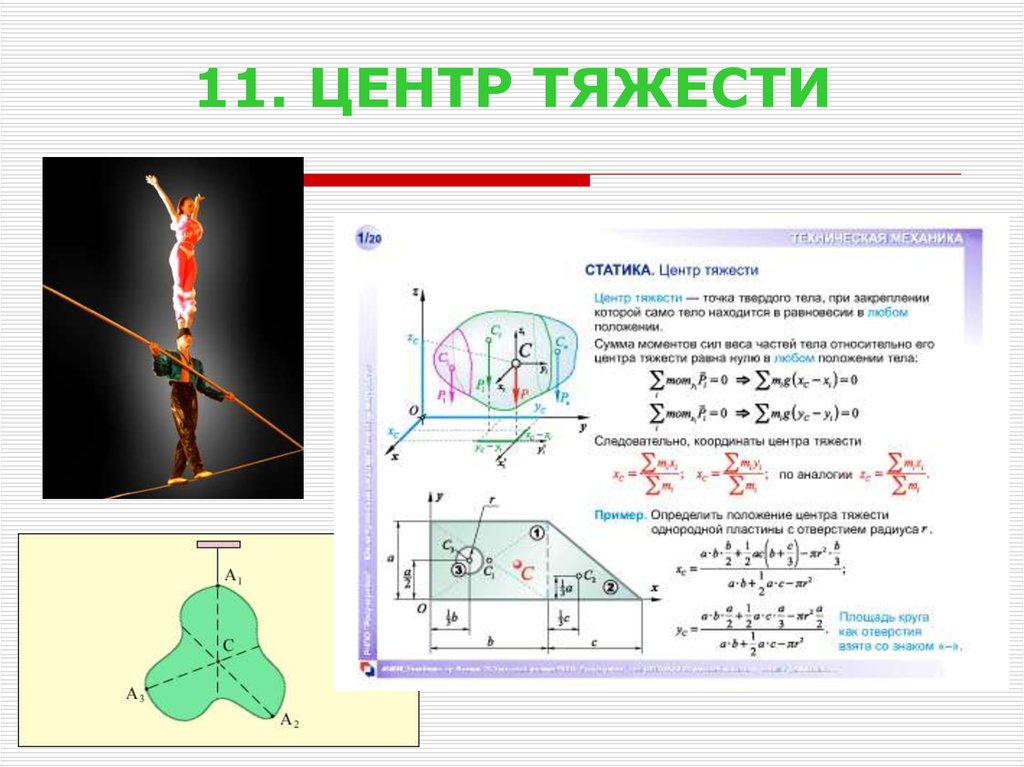
12. 11. ЦЕНТР ТЯЖЕСТИ
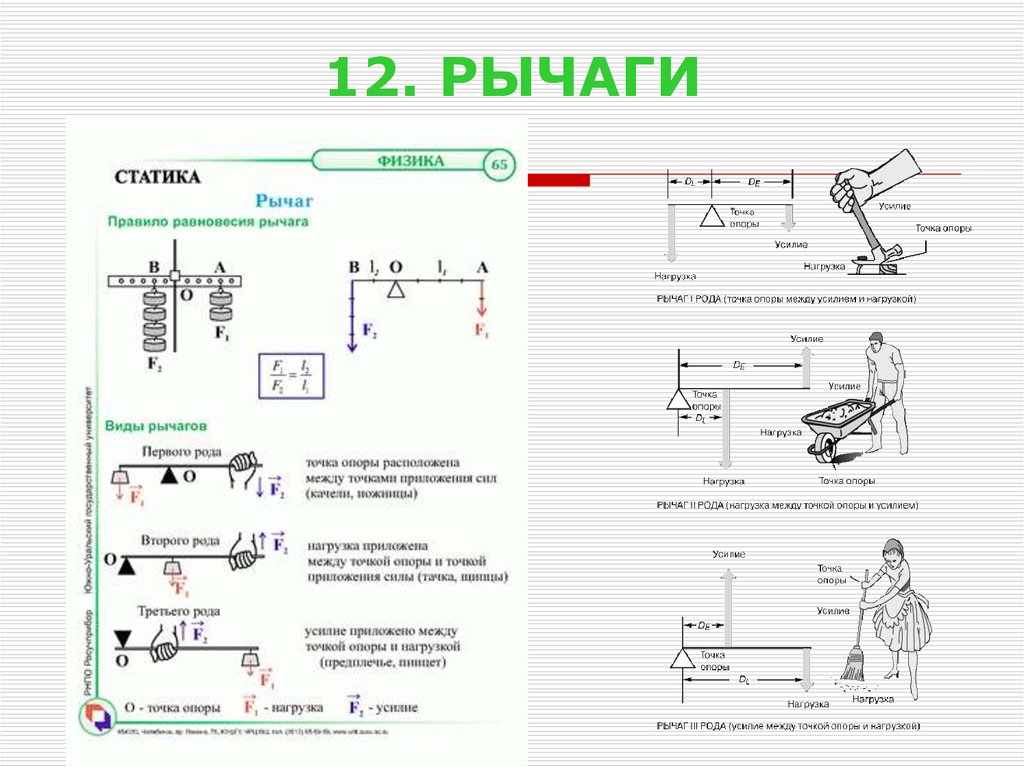
13. 12. РЫЧАГИ
14. §2. МОМЕНТ ИНЕРЦИИ
15. МОМЕНТ ИНЕРЦИИ ПРОИЗВОЛЬНОГО ТЕЛА
1. МОМЕНТ ИНЕРЦИИПРОИЗВОЛЬНОГО ТЕЛА
N
I mi Ri2 ;
i 1
m
;
V
lim
V 0
N
mi i Vi I i Ri2 Vi ;
i 1
I R dm R dV .
2
V
2
V
2
I
1
кг
м
.
кг
1 3 .
м
m dm
.
V dV
N
i const I Ri2 Vi .
i 1
const I R 2 dV .
V
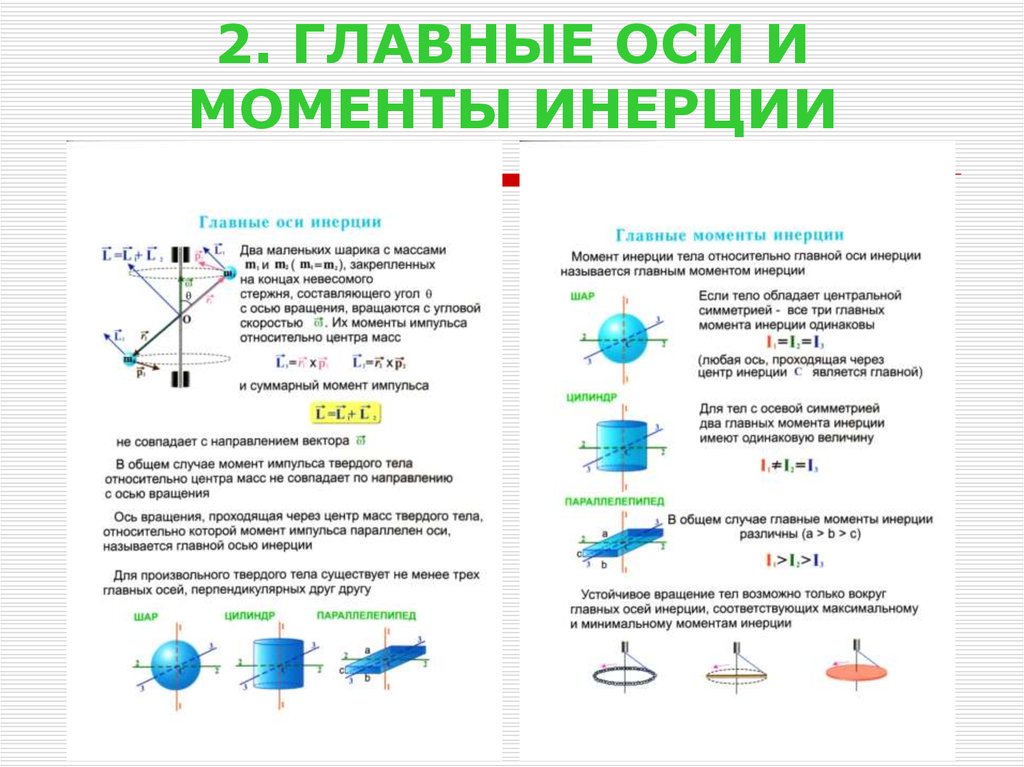
16. 2. ГЛАВНЫЕ ОСИ И МОМЕНТЫ ИНЕРЦИИ
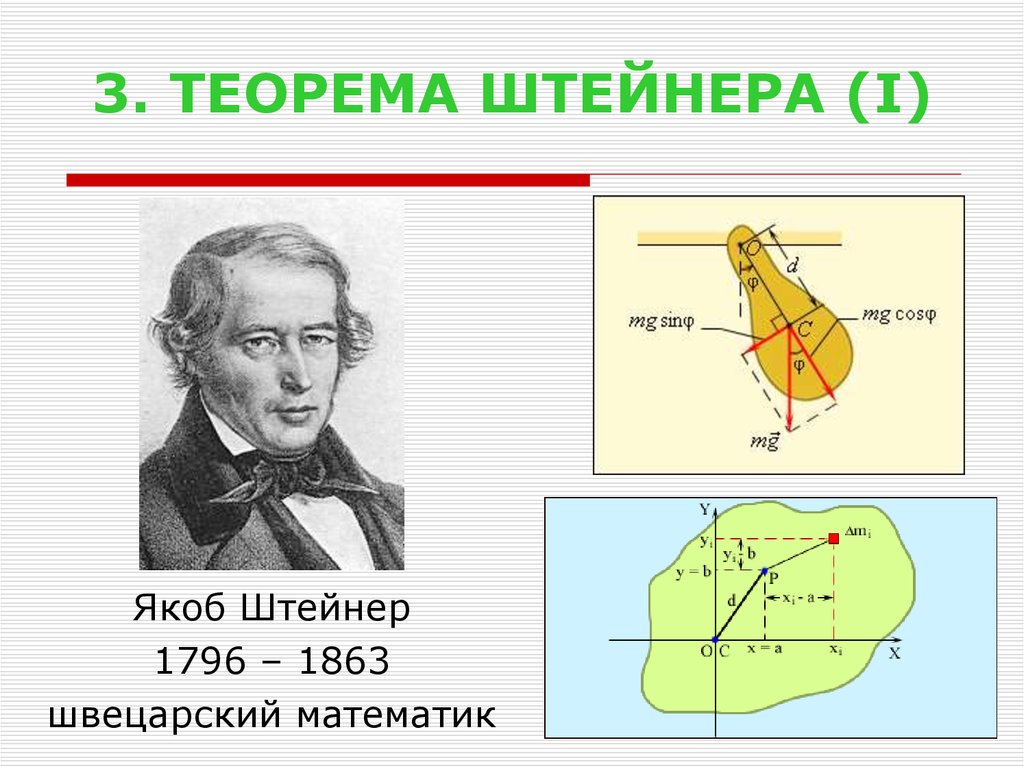
17. 3. ТЕОРЕМА ШТЕЙНЕРА (I)
Якоб Штейнер1796 – 1863
швецарский математик
18. 4. ТЕОРЕМА ШТЕЙНЕРА (II)
Момент инерции I относительно произвольной оси (ось О’) равенсумме момента инерции I c относительно оси, параллельной данной
и проходящей через центр масс тела (ось О), и произведения
массы тела m на квадрат расстояния a между осями:
I I c ma .
2
ri a ri ri a ri a 2ari ri .
'
2
'2
2
2
N
N
N
N
i 1
i 1
i 1
i 1
I mi ri '2 a 2 mi 2a mi ri mi ri 2 .
N
m r mr
i 1
i i
c
0 I ma I c .
2
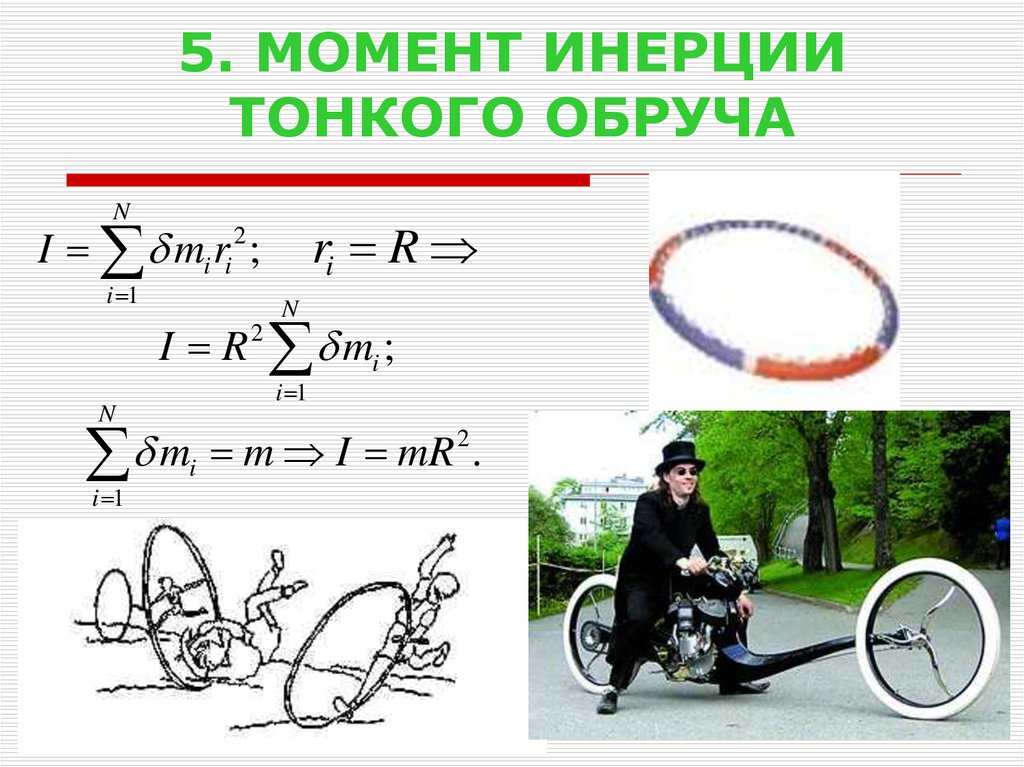
19. 5. МОМЕНТ ИНЕРЦИИ ТОНКОГО ОБРУЧА
NI mi ri 2 ;
i 1
I R
N
ri R
N
2
m ;
i 1
i
2
m
m
I
mR
.
i
i 1
20. 6. МОМЕНТ ИНЕРЦИИ ОДНОРОДНОГО СТЕРЖНЯ
mI x dm; dm dx;
l
2
l 2
l 2
m
I x dx x 2 dx
l l 2
l 2
2
l 2
3
3
2
m x
m l
l
ml
I
.
l 3 l 2 l 24 24 12
3
ml 2
l 2 ml 2
I0
m
.
12
4
3
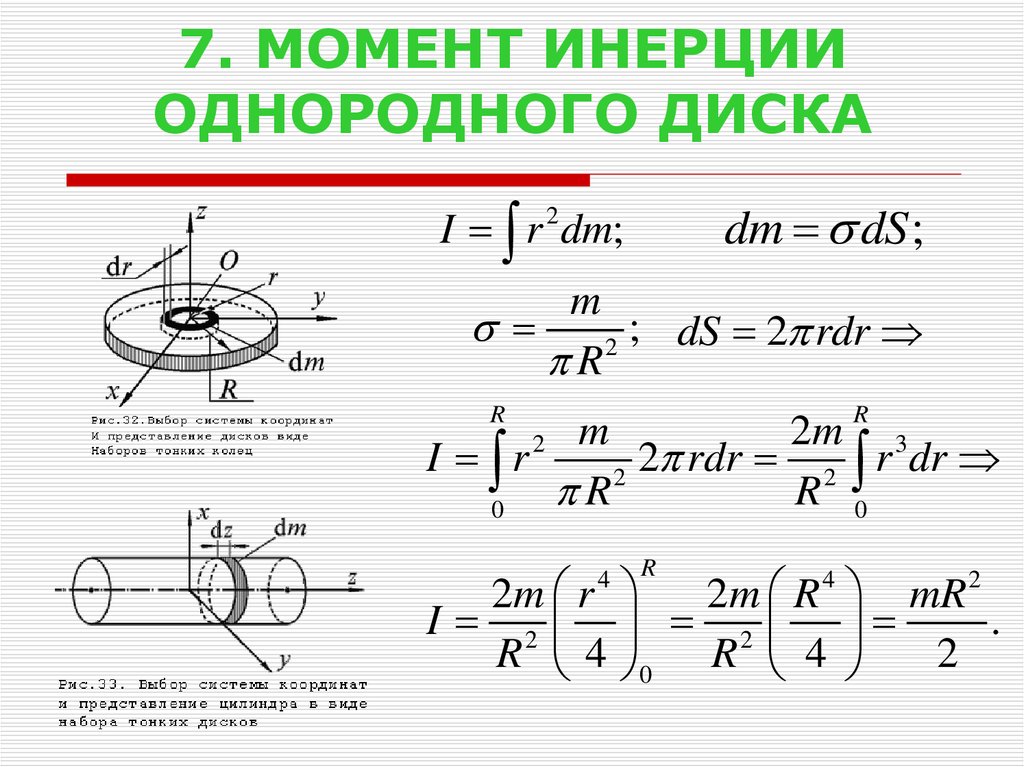
21. 7. МОМЕНТ ИНЕРЦИИ ОДНОРОДНОГО ДИСКА
dm dS ;I r 2 dm;
m
; dS 2 rdr
2
R
R
R
m
2m 3
I r
2 rdr 2 r dr
2
R
R 0
0
2
R
2m r
2m R 4 mR 2
I 2 2
.
R 4 0 R 4
2
4
22. 8. МОМЕНТ ИНЕРЦИИ ТОНКОГО ДИСКА ОТНОСИТЕЛЬНО ДИАМЕТРА
I x 2 dm; dm dS ; m ; dS 2 R 2 x 2 dx2
R
R
2 m
2
2
I 2 x
2 R x dx
2
R
0
x R cos
R
4m
2
2
2
I
x
R
x
dx.
2
R 0
dx
R
sin
d
0
4m
2
2
I
R
cos
R sin 1 R sin d
2
R 2
2
2
2
2
4 2
mR
mR
mR
2
2
2
I mR cos sin d
sin 2 d 2
.
2 0
2 2 4
0
23. 9. МОМЕНТ ИНЕРЦИИ ОДНОРОДНОЙ ТРУБКИ
I r 2 dm;dm dS ;
dS 2 rdr;
m
2
2
R2 R1
m2 rdr
2m
I r
2
2
2
2
R2 R1 R2 R1
R1
R2
2
R2
R2
r dr
3
R1
2m r
m 2
2
I 2
R
R
2
1 .
2
R2 R1 4 R
2
1
4
24. 10. МОМЕНТ ИНЕРЦИИ ТОНКОЙ СФЕРЫ
I z r 2 sin 2 m;dm
dS
m
d ; d 2 ;
4
r
dS 2 2 r sin rd
d 4 sin d m dm sin d
2
3
2
2
I z r dm sin d r dm sin ( )d cos
0
dI z r dm 1 cos d cos
2
2
1
1
1
2 2
1
3
dI z r dm cos 0 cos I mr .
0
3
3
2
25. 11. МОМЕНТ ИНЕРЦИИ ОДНОРОДНОГО ШАРА
m2 2
dI (r , dr ) r dm; dm dV ;
3
V
4 3
V R ;
dV 4 r 2dr
3
2 2 3m
2m 4
2
dI r
4 r dr 3 r dr
3
3
4 R
R
R
2m 4
2m r
2
2
I 3 r dr 3 mR .
R 0
R 5 0 5
R
5
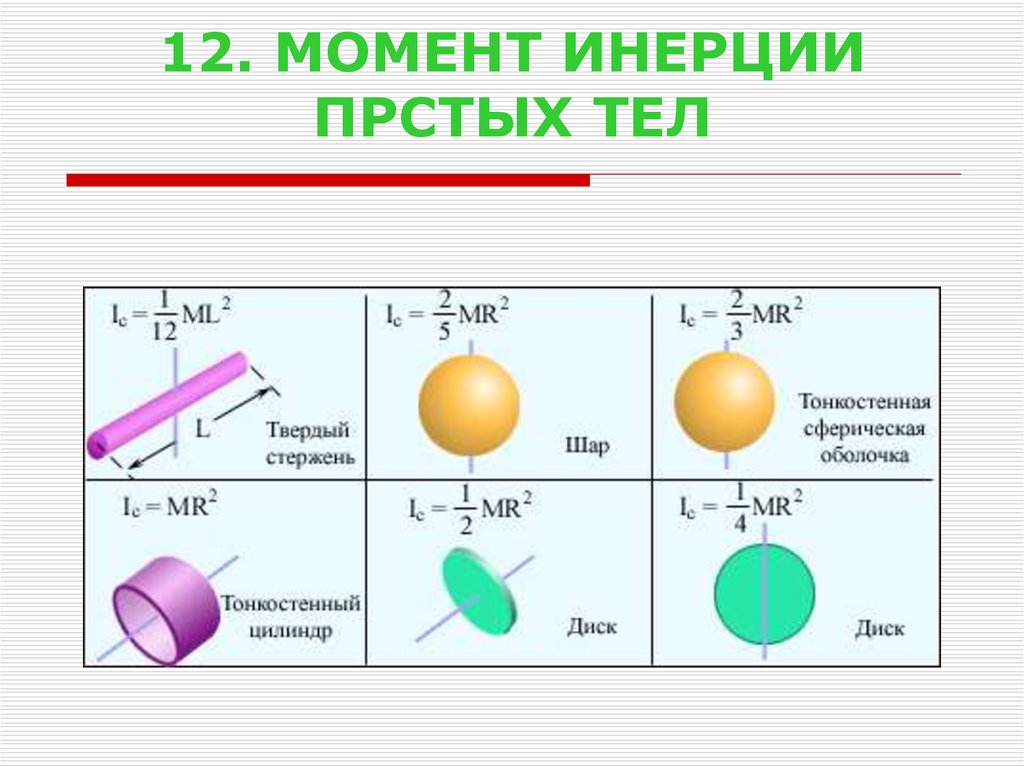
26. 12. МОМЕНТ ИНЕРЦИИ ПРСТЫХ ТЕЛ
27. §3. ЭНЕРГИЯ ВРАЩЕНИЯ
28. 1. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА
2mV
Vi Ri
Ki i i ;
2
N
mi 2 Ri2 2 N
2
K
m
R
i i .
2
2 i 1
i 1
I
mi R I K
.
2
i 1
2
N
2
i
I 2 2 L2
L I K
.
2I
2I
29. 2. РАБОТА МОМЕНТА СИЛ
dAi fi dri Fi dri fiVi dt FVi i dt .
Vi ri dAi fi ri dt Fi ri dt.
fi ri ri fi M i ;
Fi ri ri Fi M i
N
N
i 1
i 1
N
dA dAi M dt M i dt.
N
M
i 0;
i 1
N
M
i 1
i
i
i 1
M dA M dt;
2
dt d dA Md M z d ; A12 M z d .
1
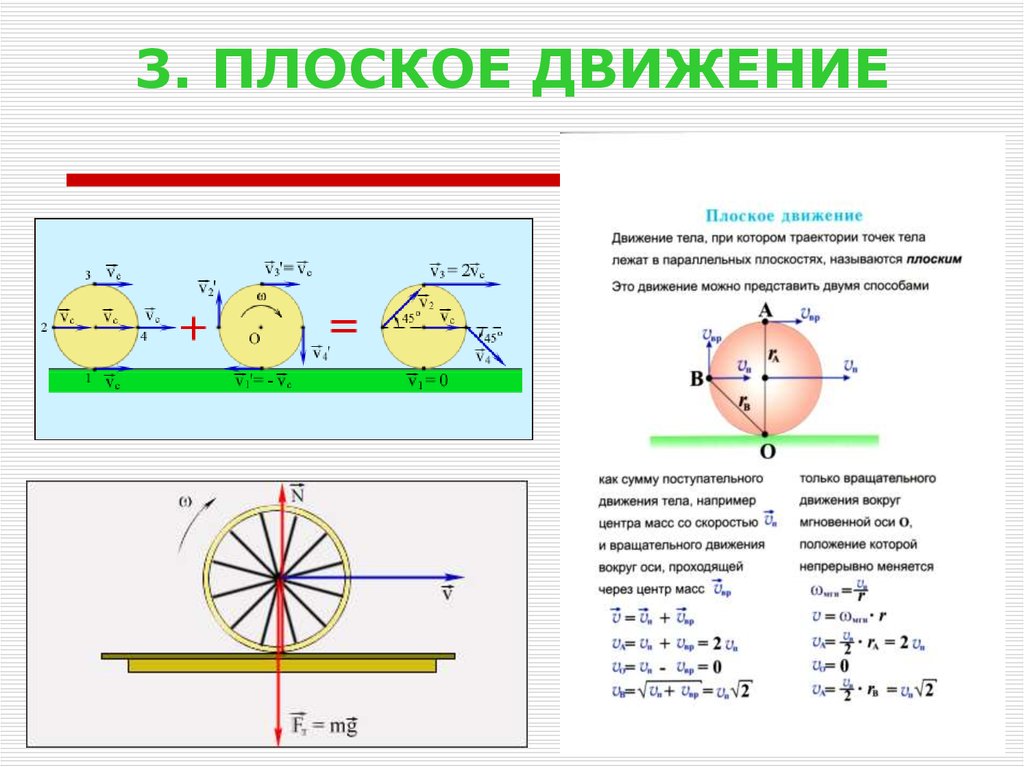
30. 3. ПЛОСКОЕ ДВИЖЕНИЕ
31. 4. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПРИ ПЛОСКОМ ДВИЖЕНИИ
22
mV
m
i
i
i
Vi V0 ri ;
Ki
Ki
V0 ri
2 2
2
mi 2
Ki
V0 2V0 ri ri . ri ri sin Ri
N
2
mi 2
Ki
V0 2 V0 ri 2 Ri2 . K K i
2
i 1
2 N
N
V0
2 N
2
K
m
V
m
r
m
R
i
0
i i
i i .
2 i 1 N
2 i 1
i 1
N
N
mi m;
i 1
mi ri mrc ;
i 1
2
m
R
i i I0
i 1
2
mV02
I 0
K
mrc V0
.
2
2
mVc2 I c 2
rc 0 K
.
2
2
32. §4. ГИРОСКОПЫ
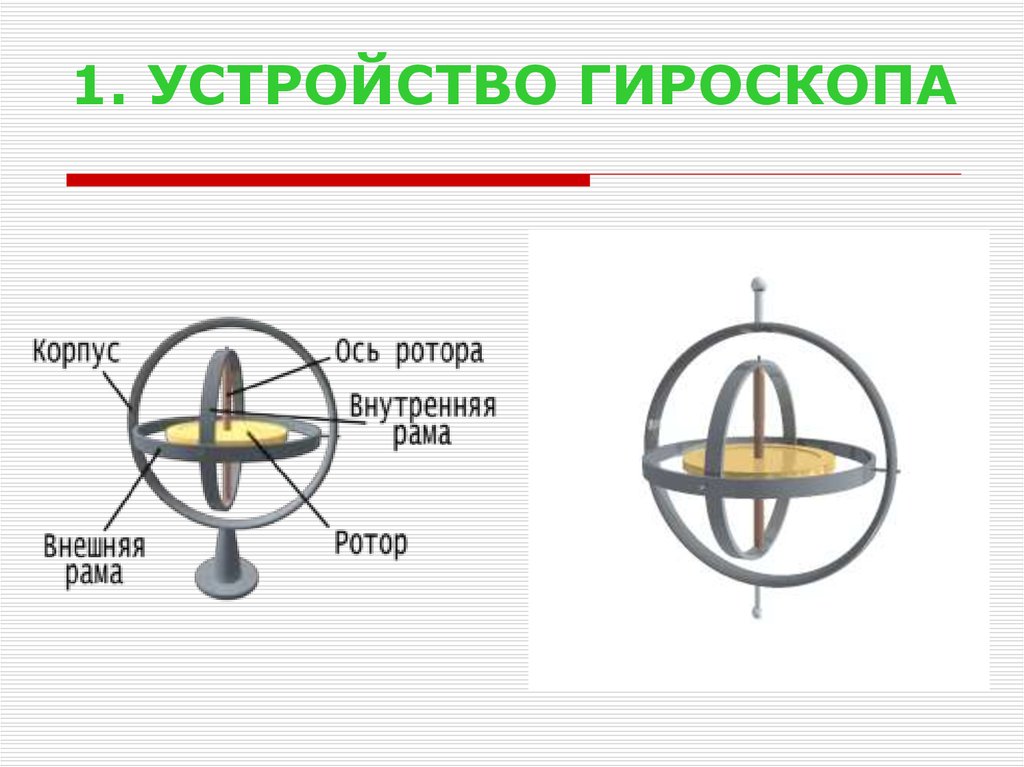
Гироскопом (иливолчком)
называется
массивное
симметричное тело,
вращающееся с
большой скоростью
вокруг оси симметрии
(оси гироскопа).
33. 1. УСТРОЙСТВО ГИРОСКОПА
34. 2. ГИРОСКОПИЧЕСКИЙ ЭФФЕКТ
Гироскопический эффектсостоит в том, что под
действием внешней силы,
перпендикулярной моменту
импульса, ось гироскопа
поворачивается в плоскости,
содержащей момент импульса
гироскопа и момент внешней
силы ( перпендикулярной
моменту импульса и силе).
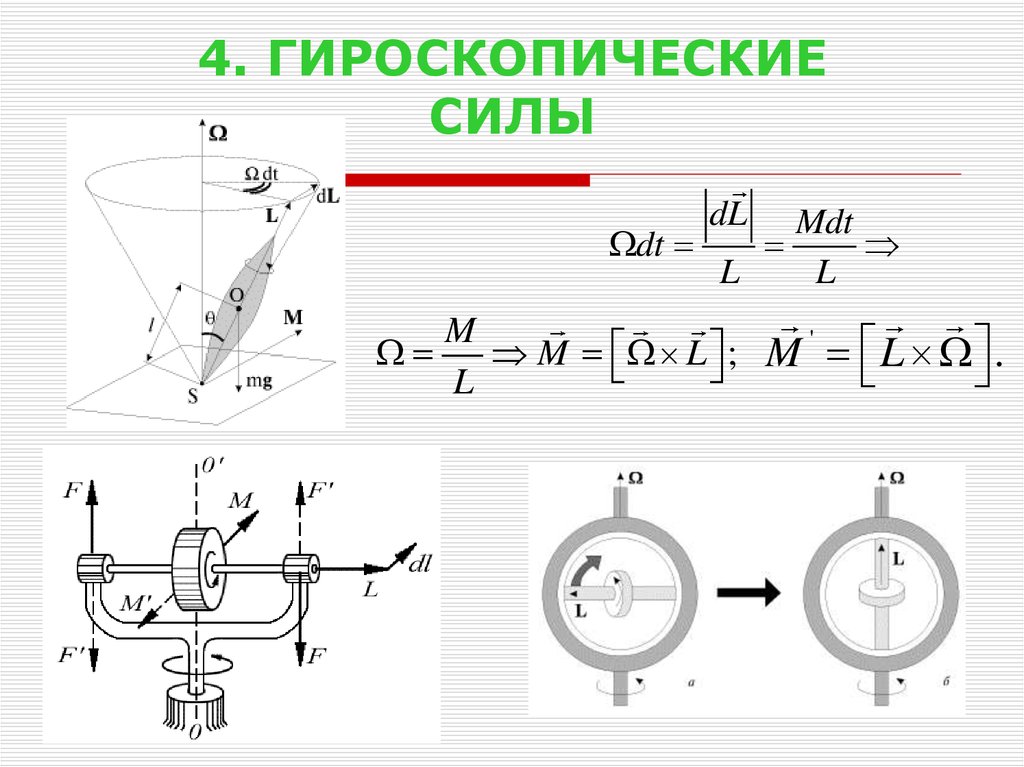
35. 4. ГИРОСКОПИЧЕСКИЕ СИЛЫ
dLMdt
dt
L
L
M
M L ; M ' L .
L
36. 5. ГИРОКОМПАС
Гироскопическим компасом (гирокомпасом)называется гироскоп, ось которого может
свободно поворачиваться в горизонтальной
плоскостипод влиянием суточного
Вращения Земли.
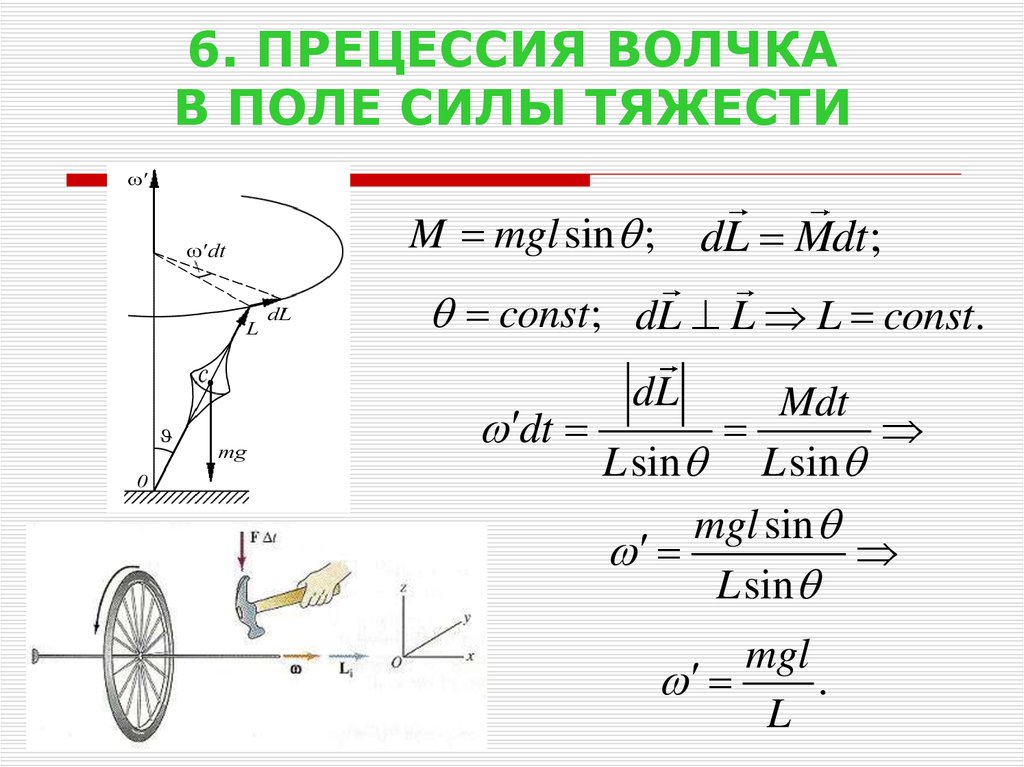
37. 6. ПРЕЦЕССИЯ ВОЛЧКА В ПОЛЕ СИЛЫ ТЯЖЕСТИ
M mgl sin ;dL Mdt;
const ; dL L L const.
dL
Mdt
dt
L sin L sin
mgl sin
L sin
mgl
.
L





















 Физика
Физика








