Работа, мощность, механическая энергия

1.

2.

.
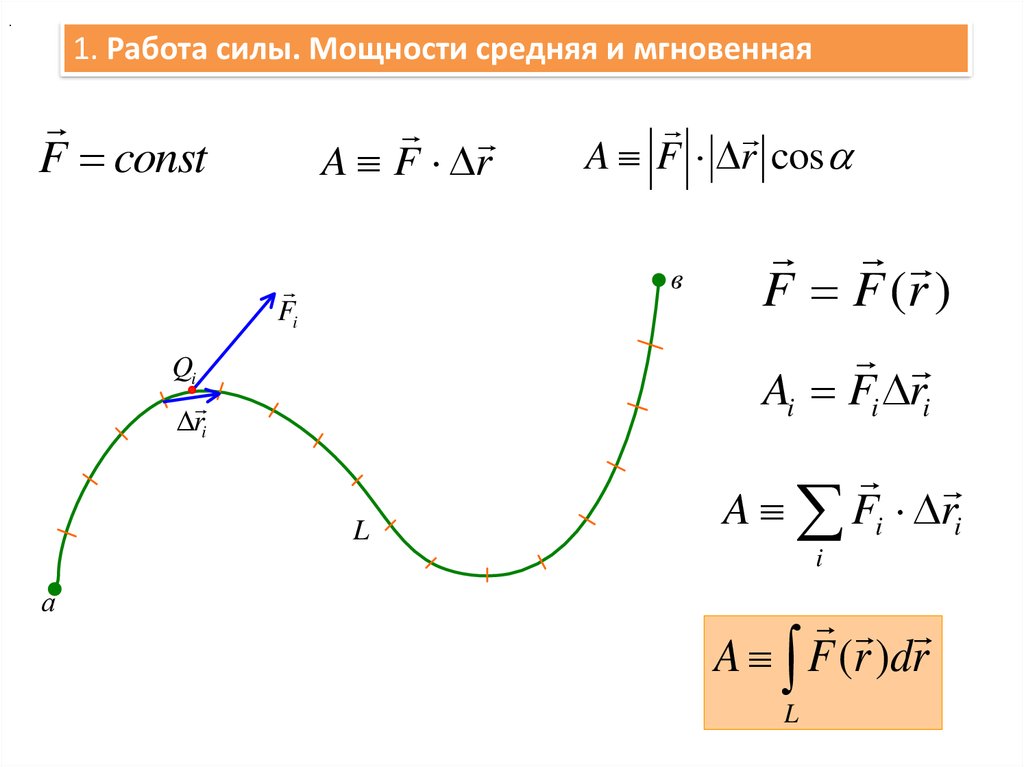
1. Работа силы. Мощности средняя и мгновенная
F const
A F r
A F r cos
в
Fi
F F (r )
Ai Fi ri
Qi
ri
L
A Fi ri
i
а
A F (r )dr
L

3.

.
A F ( r )dr
А
N ср
t
N
A
dt
- бесконечно малая работа –
(элементарная работа) , работа силы F
на бесконечно малом перемещении dr
-средняя за промежуток времени
мощность силы
-мгновенная мощность силы
N F
Сила, перпендикулярная скорости, имеет нулевую мощность и
работы не совершает. Такова сила Лоренца.
t1 , t2

4.

.
2. Кинетическая энергия системы. Теорема о кинетической
энергии.
m
Ек
2
2
- кинетическая энергия материальной точки
Кинетическая энергия материальной точки – это величина,
численно равная работе, которую нужно совершить, чтобы
сообщить первоначально покоившейся материальной точке
данную скорость
Теоремой о кинетической энергии
Изменение кинетической энергии механической системы
за некоторый промежуток времени равно сумме работ
вcех сил, действующих на систему.
m 2
m 1
A
2
2
2
2

5.

3. Консервативные и неконсервативные силы.
Потенциальная энергия
Опр.1. Сила называется консервативной, если работа силы
над материальной точкой при ее перемещении из точки а в
точку в не зависит от формы отрезка траектории L,
соединяющего а и в, а определяется только начальным (а) и
конечным (в) положениями материальной точки.
Опр. 2. Сила называется консервативной, если ее работа
над материальной точкой на любом замкнутом контуре
равна нулю.
F
(
r
)
d
r
0
- циркуляция вектора
F
L
Примеры консервативных сил: сила тяжести, сила
упругости, кулоновская сила.
Неконсервативны все виды сил трения, сила Лоренца.

6.

dЕп Fdr
-используется для вычисления потенциальной
энергии м.т. в потенциальных силовых полях
F grad Еп " grad "
-градиент- дифференциальный
оператор
Еп Еп Еп
grad Еп
i
j
k
x
y
z
Еп
Fx
x
Еп
Fy
y
Еп
Fz
z

7.

Консервативная сила
F const
F qE
F mg
Fx kx
m1m2 r
F G 2
r
r
qq r
F k0 1 2 2
r
r
Потенциальная энергия
Åï F r
Åï qE r
Еп mgh
kx2
Еп
2
m1m2
Åï ( r ) G
r
q1q2
Еп ( r ) k 0
r

8.

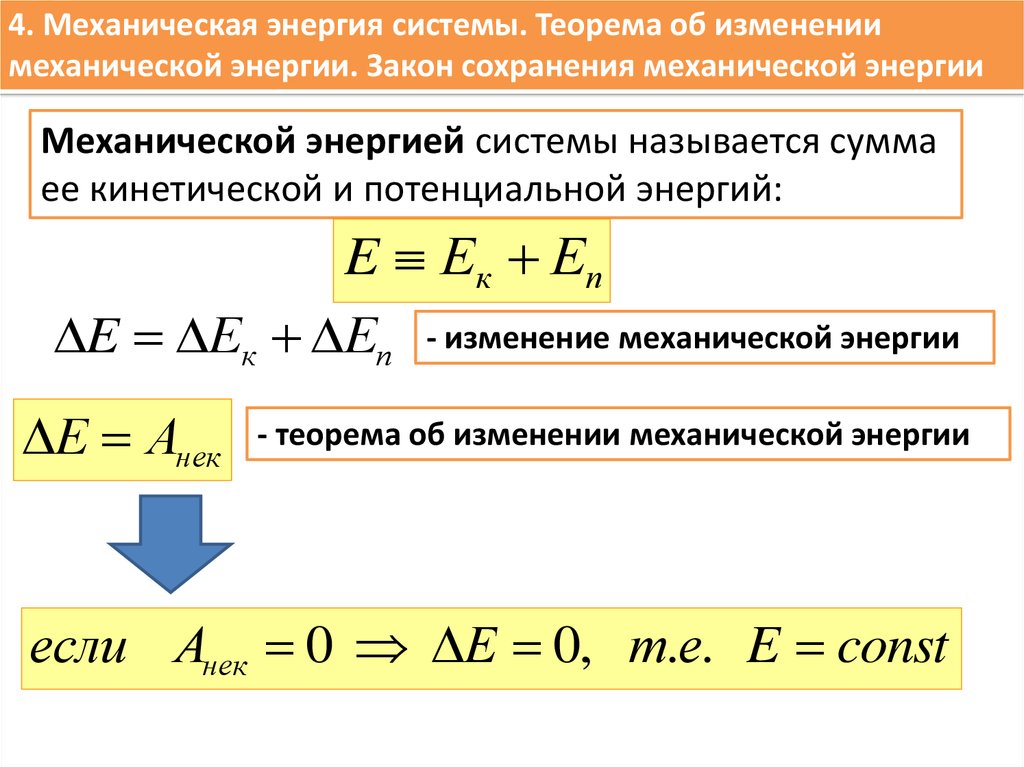
4. Механическая энергия системы. Теорема об изменении
механической энергии. Закон сохранения механической энергии
Механической энергией системы называется сумма
ее кинетической и потенциальной энергий:
E Ек Еп
E Ек Еп
Е Анек
- изменение механической энергии
- теорема об изменении механической энергии
если Анек 0 Е 0, т.е. E const

9.

Закон сохранения
механической энергии:
если сумма работ неконсервативных сил,
действующих на систему, за любой промежуток
времени равна нулю, то механическая энергия
системы сохраняется.
Традиционная формулировка закона сохранения механической энергии:
если все силы, действующие на механическую систему,
консервативны, то механическая энергия системы
сохраняется.