Логические основы ЭВМ

1. Логические основы ЭВМ

Лектор Лузев В.С.

2.

• Алгебра логики — это раздел
математики, изучающий высказывания,
рассматриваемые со стороны их
логических значений (истинности или
ложности) и логических операций над
ними.

3.

- Алгебра высказываний
(Булева алгебра)
Основатель - английский
математик
Джордж Буль(1815 – 1864),
ввёл алфавит, орфографию
и грамматику для
математической логики.

4.

Что же такое « логическое высказывание»?
Логическое высказывание —
это любoе повествовательное
пpедлoжение, в oтнoшении
кoтopoгo мoжно oднoзначнo
сказать, истиннo (True) oнo
или лoжнo (False).

5.

Например, высказыванием является предложение «пять
на пять – двадцать пять», так как оно истинное.
Предложение «пять плюс 2 равно восьми" тоже
высказывание, так как оно ложное.
Вопросительные предложения («Какой русский не любит
быстрой езды?» (Н. В. Гоголь)) или побудительные
предложения («Мой друг! Отчизне посвятим души
прекрасные порывы» (А. С. Пушкин).) не являются
логическими высказываниями.

6.

Чтобы обращаться к логическим высказываниям, им
назначают имена. Пусть через А обозначено высказывание
«Игорь был летом на море", а через В — высказывание
«Костя летом был на сплаве". А, В — логические
переменные, которые могут принимать только два значения
—
"истина"
или
"ложь",
обозначаемые,
соответственно, "1" и "0".

7.

Логические операции
Название
Обозначение
Математическое
обозначение
Логическое умножение,
конъюнкция
И, AND
&, ,/\
Логическое сложение,
дизъюнкция
ИЛИ, OR
+,\/
Логическое отрицание,
инверсия
НЕ, NOT
Импликация,
следование
Если … то (А imp В)
Эквивалентность,
равносильность
тогда и только тогда

8. Элементарные логические операции

1 Конъюнкция(от лат. conjunctio союз, связь)
Определение. Соединение двух (или несколько) высказываний в одно с
помощью союза И (AND) называется конъюнкцией (или операцией
логического умножения). Обозначаются ˄, &,•. (амперсенд)
Значения логических операций определяются по правилам,
задаваемым в таблице истинности.
А
В
A&B =F
0
0
0
0
1
0
1
0
0
1
1
1

9.

2 Дизъюнкция(лат. disjunctio — разобщение)
Определение. Соединение двух (или несколько) высказываний в
одно с помощью союза ИЛИ (OR) называется дизъюнкцией (или
логическим сложением).
Обозначаются ˅, +.
Таблица истинности
A
0
0
1
1
B
0
1
0
1
F=AVB
0
1
1
1
Xor-модифицированная операция «ИЛИ» исключающее или (хor), от
обычного «ИЛИ» отличается последней строкой.

10.

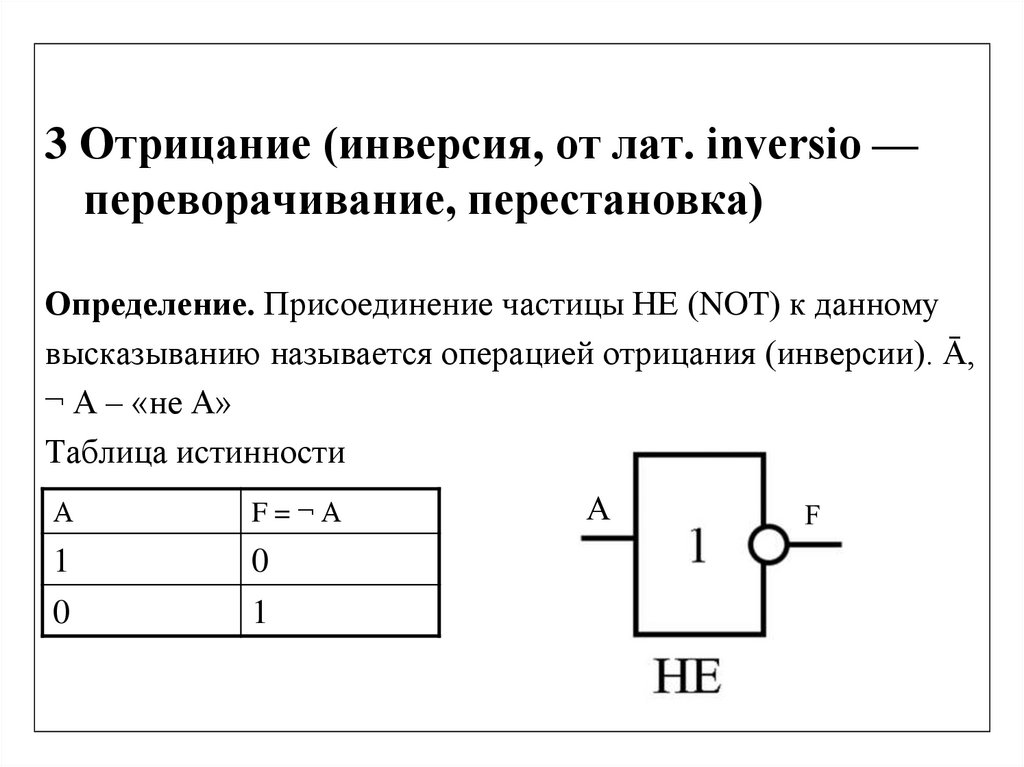
3 Отрицание (инверсия, от лат. inversio —
переворачивание, перестановка)
Определение. Присоединение частицы НЕ (NOT) к данному
высказыванию называется операцией отрицания (инверсии). Ā,
¬ А – «не А»
Таблица истинности
А
F=¬А
1
0
0
1

11.

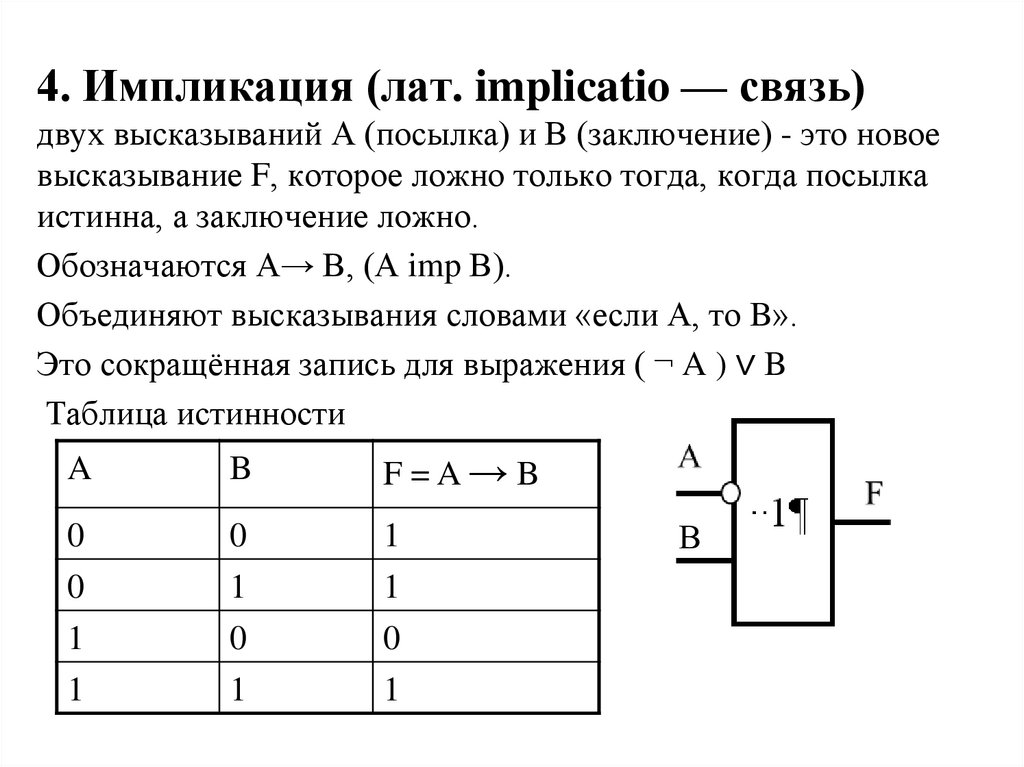
4. Импликация (лат. implicatio — связь)
двух высказываний А (посылка) и В (заключение) - это новое
высказывание F, которое ложно только тогда, когда посылка
истинна, а заключение ложно.
Обозначаются А→ В, (А imp В).
Объединяют высказывания словами «если А, то B».
Это сокращённая запись для выражения ( ¬ A ) ∨ B
Таблица истинности
A
B
F=A→B
0
0
1
1
0
1
0
1
1
1
0
1

12.

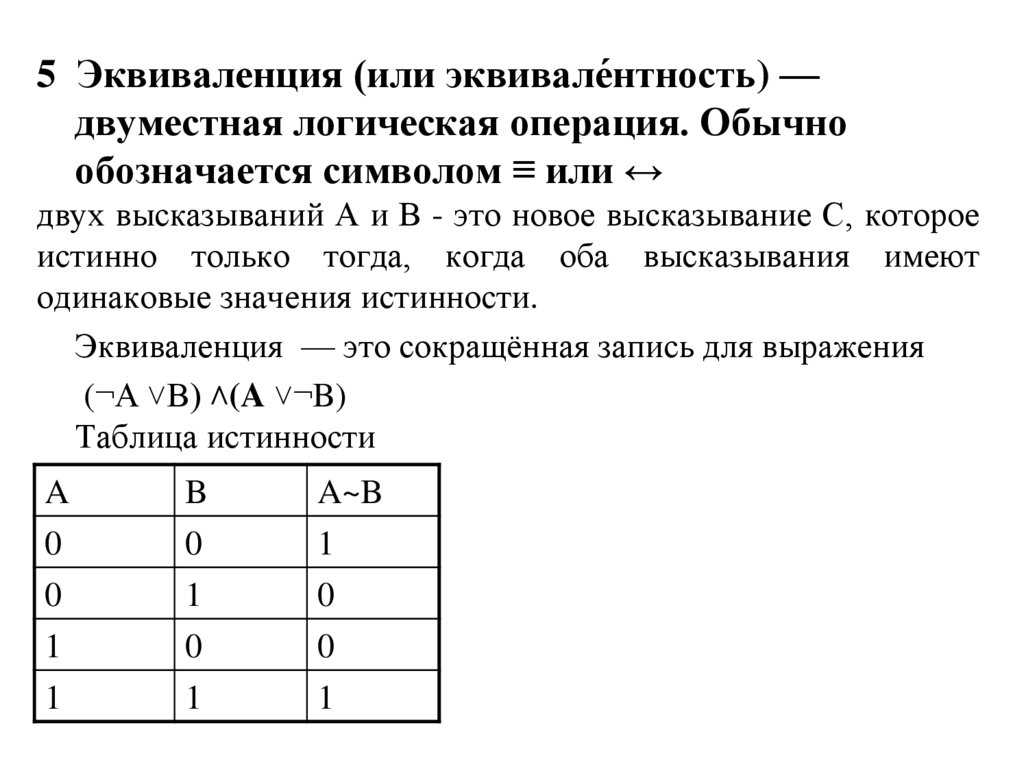
5 Эквиваленция (или эквивале́нтность) —
двуместная логическая операция. Обычно
обозначается символом ≡ или ↔
двух высказываний А и В - это новое высказывание С, которое
истинно только тогда, когда оба высказывания имеют
одинаковые значения истинности.
Эквиваленция — это сокращённая запись для выражения
(¬A ˅B) ˄(A ˅¬B)
Таблица истинности
A
0
B
0
A~B
1
0
1
1
1
0
1
0
0
1

13. Порядок выполнения логических операций в сложном логическом выражении

1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения
логических операций используются скобки.

14.

Высказывания, образованные с помощью нескольких
логических операций называются сложными. Истинность их
устанавливают, используя таблицы истинности
соответствующих операций.
_
_
Пример: определим истинность сложного высказывания А & В
A
0
B
0
_
A
1
_
B
1
_ _
A&B
1
0
1
1
0
0
1
0
0
1
0
1
1
0
0
0

15. Схемная реализация базовых логических элементов.

Логические элементы (ЛЭ)- это электронные схемы с одним или
несколькими входами и одним выходом, через которые проходят
электрические сигналы, представляющие 0 или 1.
Для реализации любой логической операции над двоичными сигналами
достаточно элементов трёх типов: И, ИЛИ, НЕ, функционально полная
система, все остальные можно построить через них.
Из логических элементов путём их комбинации строятся основные схемы
компьютера.

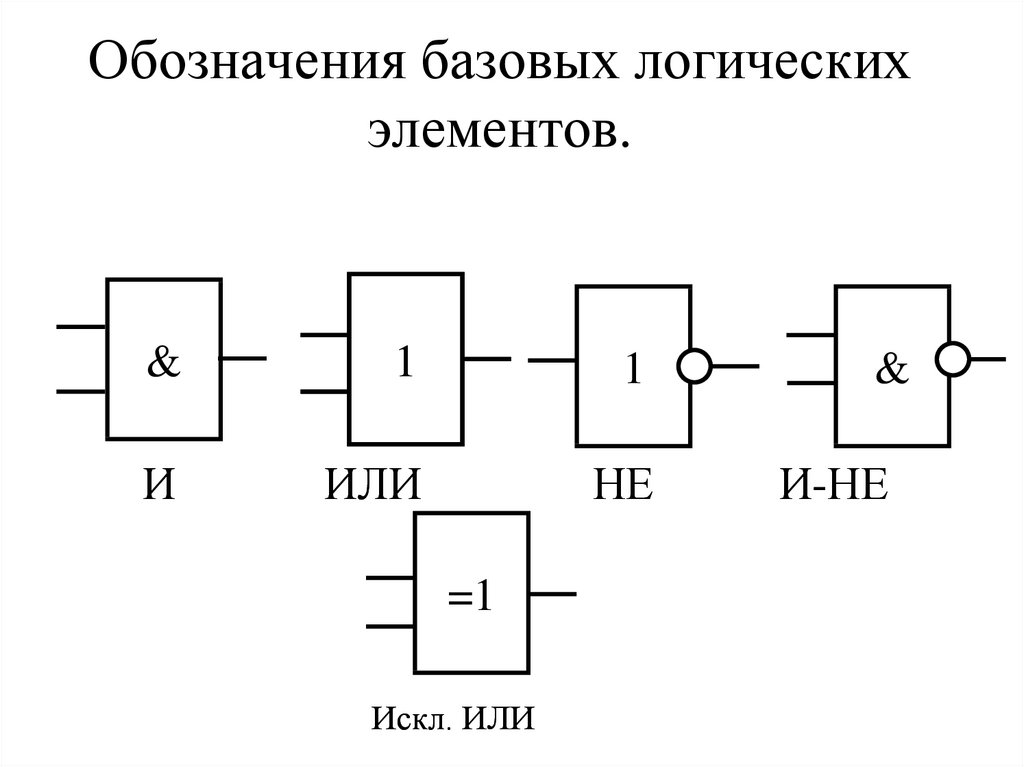
16. Обозначения базовых логических элементов.

&
1
1
И
ИЛИ
НЕ
=1
Искл. ИЛИ
&
И-НЕ

17.

Логическая схема асинхронного RSтриггера на элементах 2И–НЕ
Триггер - электронный прибор,
имеющий два устойчивых
состояния, является типичным
запоминающим элементом,
способным хранить 1 бит
информации.

18.

• Регистром называется функциональный узел,
осуществляющий приём, хранение и передачу
информации. Регистры состоят из группы
триггеров, обычно D. По типу приёма и выдачи
информации различают 2 типа регистров:
• С последовательным приёмом и выдачей
информации — сдвиговые регистры.
• С параллельным приёмом и выдачей
информации — параллельные регистры.

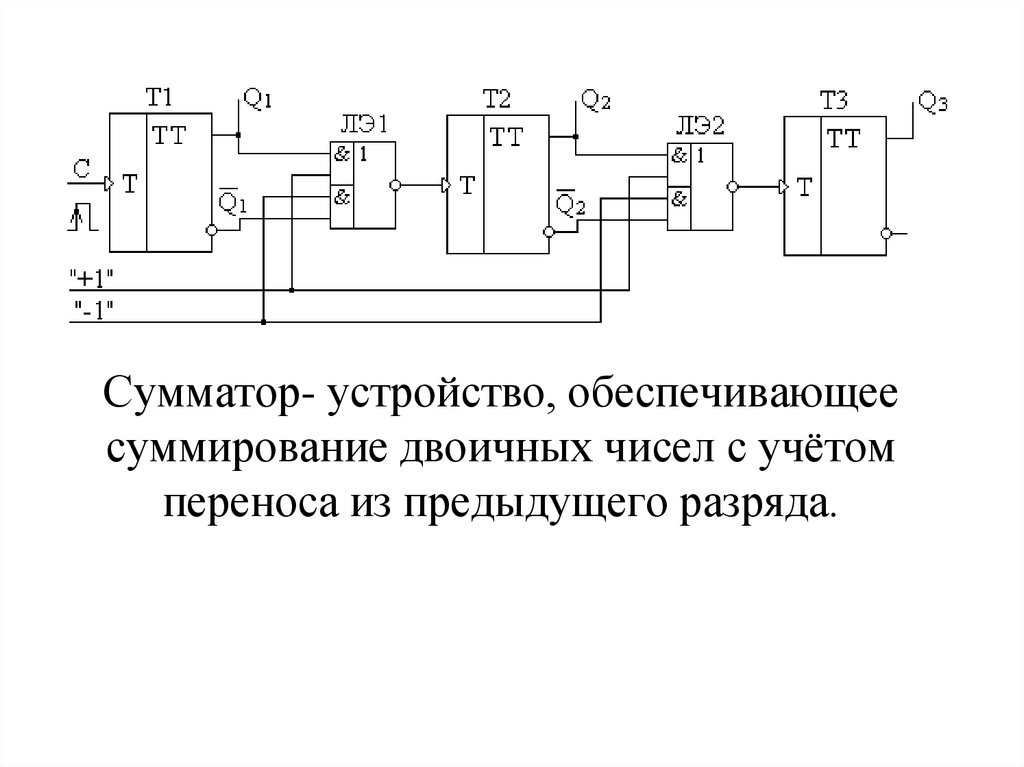
19. Сумматор- устройство, обеспечивающее суммирование двоичных чисел с учётом переноса из предыдущего разряда.

20.

21.

Логическое выражение
значениях переменных А, В, С:
будет истинным при следующих
Решение:
Логическое выражение
будет истинным при значениях переменных
Подставив эти значения в исходное выражение, получим:
0 0 И 0 2
То есть значение заданного выражения истинно.
При других приведённых комбинациях значений А, В, С заданное логическое выражение
принимает значение ЛОЖЬ.