Теория поведения потребителя на рынке

1. Теория поведения потребителя на рынке

2. Теория поведения потребителя на рынке

1. Решение задачи максимизации функции
полезности при бюджетном ограничении.
2. Решение задачи минимизации расхода
потребителя при фиксированном уровне
полезности.
3. Уравнения Слуцкого.
4. Оценка изменения благосостояния
потребителя.

3. 1.Решение задачи максимизации функции полезности при бюджетном ограничении.

Основные характеристики потребителя:
• Функция полезности U(x1,x2,… хn).
• Доход потребителя (М)
Основные характеристики рынка:
• Потребительские наборы товаров (хn)
• Цены товаров (р)

4. 1.Решение задачи максимизации функции полезности при бюджетном ограничении.

U(x1,x2) → max при
p1x1+ p2x2 = M
p1x1+ p2x2 = M → min при
U(x1,x2) =

5. 1.Решение задачи максимизации функции полезности при бюджетном ограничении.

L(x1, x2,λ) = U(x1,x2)+ λ(M- p1x1- p2x2)
Условия экстремума функции полезности при наличии бюджетного
ограничения:
=0 =0 =0
M – p1x1– p2x2 = 0

6. 1.Решение задачи максимизации функции полезности при бюджетном ограничении.

Критическая точка (, ,) – длинная точка,
Критическая точка (, ,) – короткая точка.
Функции:
= D1(p1, p2,M),
= D2(p1, p2,M),
– функции спроса по Маршаллу (по Вальрасу) на первый и второй продукт со
стороны потребителя.

7. 1.Решение задачи максимизации функции полезности при бюджетном ограничении.

U ( = U(D1(p1, p2,M), D2(p1, p2,M))=ν(p1, p2,M) – косвенная (неявная)
функция полезности.
Свойства косвенной функции полезности:
1. Косвенная функция является однородной функцией нулевой степени
по всем переменным, то есть для любого γ>0:
γ0 ν (p1, p2,M) = ν (γp1, γp2, γM)
2. Повышение дохода потребителя ведет к росту ν (p1, p2,M).
3. Увеличение цены товара уменьшает ν (p1, p2,M).
4. Функция выпуклая.
5. Функция непрерывная.

8. 1.Решение задачи максимизации функции полезности при бюджетном ограничении.

6. Предельная полезность по доходу равна множителю Лагранжа:
=
Это утверждение позволяет оценить новое максимальное значение
функции полезности, которое получается при относительно малом
изменении дохода:
+
7. Предельная полезность по цене продукта равна:
= – тождество Роя
Тождество Роя позволяет оценить новое максимальное значение
функции полезности, которое получается при относительно малом
изменении цены продукта.
+

9. 2.Решение задачи минимизации расхода потребителя при фиксированном уровне полезности.

L(x1, x2,λ) = p1x1+ p2x2 + λ(- U(x1,x2))
Условия экстремума:
= p1– λ =0
= p2 – λ =0
=- U(x1,x2)=0

10. 2.Решение задачи минимизации расхода потребителя при фиксированном уровне полезности.

Решение системы уравнений:
– ( ,,) – длинная точка;
– (,) – короткая точка, характеризующая экстремум функции.
Функции:
, = H1(p1, p2,),
= H2(p1, p2,),
– функции спроса по Хиксу (функции компенсированного спроса) на
первый и второй продукт со стороны потребителя.

11. 2.Решение задачи минимизации расхода потребителя при фиксированном уровне полезности.

Функции спроса: , = H1(p1, p2,), = H2(p1, p2,) подставляем в целевую
функцию = p1+ p2
и получаем функцию расходов:
= m(p1, p2,) =p1 H1(p1, p2,)+ p2 H2(p1, p2,).

12. 2.Решение задачи минимизации расхода потребителя при фиксированном уровне полезности.

Свойства функции расходов:
1.Функция расходов однородна первой степени по переменным p 1 и p2,
то есть для любого γ>0:
m(γ p1, γ p2,) = γ m(p1, p2,)
2. Если заданная полезность , p1 или p2 увеличиваются, то m(p1,p2,)
возрастает.
3. Функция расходов выпуклая вверх по переменным p1 и p2.
4.Функция расходов непрерывна.
5. Предельный расход по полезности равен множителю Лагранжа:
=
Это утверждение позволяет оценить новое минимальное значение
функции расходов, которое получается при относительно малом
изменении заданной полезности:
+

13. 2.Решение задачи минимизации расхода потребителя при фиксированном уровне полезности.

Свойства функции расходов:
6.Предельный расход по цене товаров равен:
= – лемма Шепарда
Лемма Шепарда позволяет оценить новое минимальное значение
функции расходов, которое получается при относительно малом
изменении цены продукта.
+

14. 3. Уравнения Слуцкого.

В функцию спроса D1(p1, p2,M) подставим уровень дохода, равный
минимальному расходу для достижения заданного уровня полезности :
М= m(p1, p2,).
Тогда значениями функций спроса по Маршаллу и по Хиксу будет
являться один и тот же объем потребления товара и = .
То есть:
D1(p1, p2, m(p1, p2,)) = H1(p1, p2,)
D2(p1, p2, m(p1, p2,))= H2(p1, p2,)

15. 3. Уравнения Слуцкого.

Найдем частную производную:
=+ *
Учитывая, что:
= H2() – лемма Шепарда
и D2(p1, p2, m(p1, p2,)) = H2(p1, p2,)
Получим уравнение Слуцкого:
= + *D2

16. 3. Уравнения Слуцкого.

= + *D2
Или
=– *D2
После деления на D1 = Н1 и умножения на p2 получаем:
* =*–* *D2
Преобразуем последнее слагаемое:
* *D2 = * *

17. 3. Уравнения Слуцкого.

Получаем:
* =*– * *
* – коэффициент перекрестной эластичности спроса (по Маршаллу) на
2-ый продукт по цене 2-го продукта.
*– коэффициент перекрестной эластичности спроса (по Хиксу) на 1-ый
продукт по цене 2-го продукта.
* – эластичность спроса по доходу.
– доля дохода потребителя, который он тратит на приобретение 2-го
продукта.

18. 4. Оценка изменения благосостояния потребителя

Пусть имеется уравнение бюджетной плоскости:
p1X1 + p2x2 + ... + pnxn = M1
Его можно представить:
p1x1 + y = M1,
где y=p2 X2 + ... + pnxn — количество композитного продукта (товара).

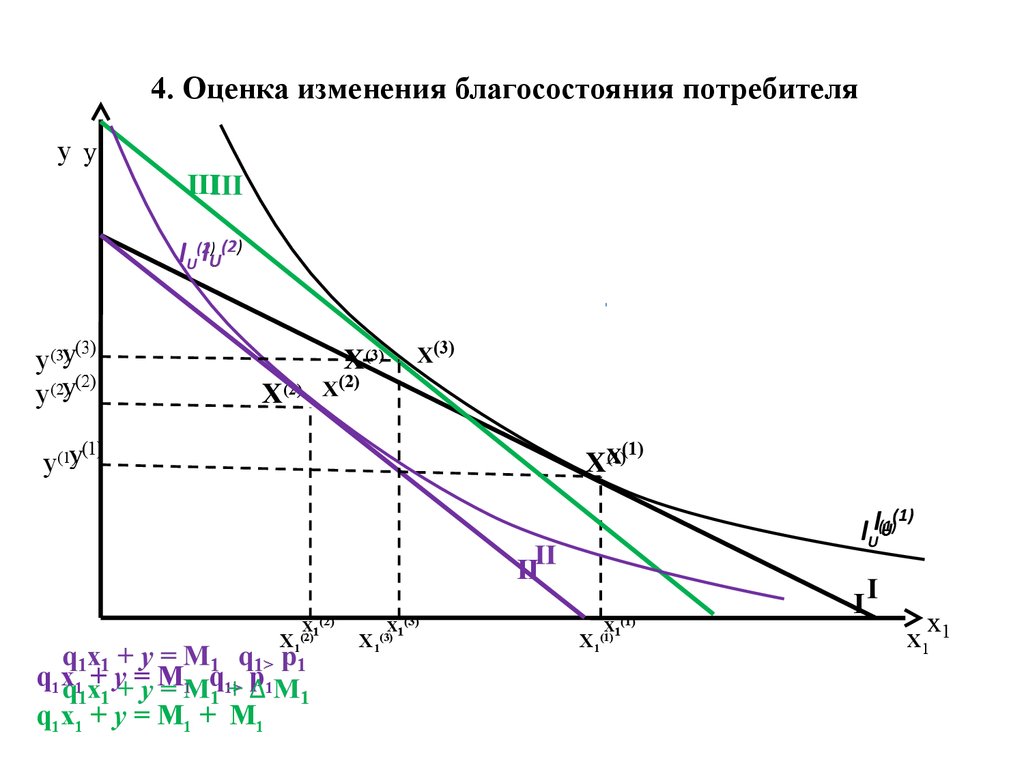
19. 4. Оценка изменения благосостояния потребителя

y
III
lU(2)
y(3)
y(2)
X(3)
X(2)
y(1)
X(1)
lU(1)
II
I
X1(2)
q1x1 + y = M1 q1> p1
q 1 x 1 + y = M 1 + M1
X1(3)
X1(1)
x1

20. 4. Оценка изменения благосостояния потребителя

Переход x(2) → x(1) — общий эффект (ОЭ)
Переход x(3) → x(1) — эффект замены (ЭЗ)
Переход x(2) → x(3) — эффект дохода (ЭД)
ОЭ = ЭЗ + ЭД

21. 4. Оценка изменения благосостояния потребителя

Формула ОЭ = ЭЗ + ЭД наглядно интерпретирует уравнение Слуцкого:
=– *D2
(ОЭ) (ЭЗ) (ЭД)

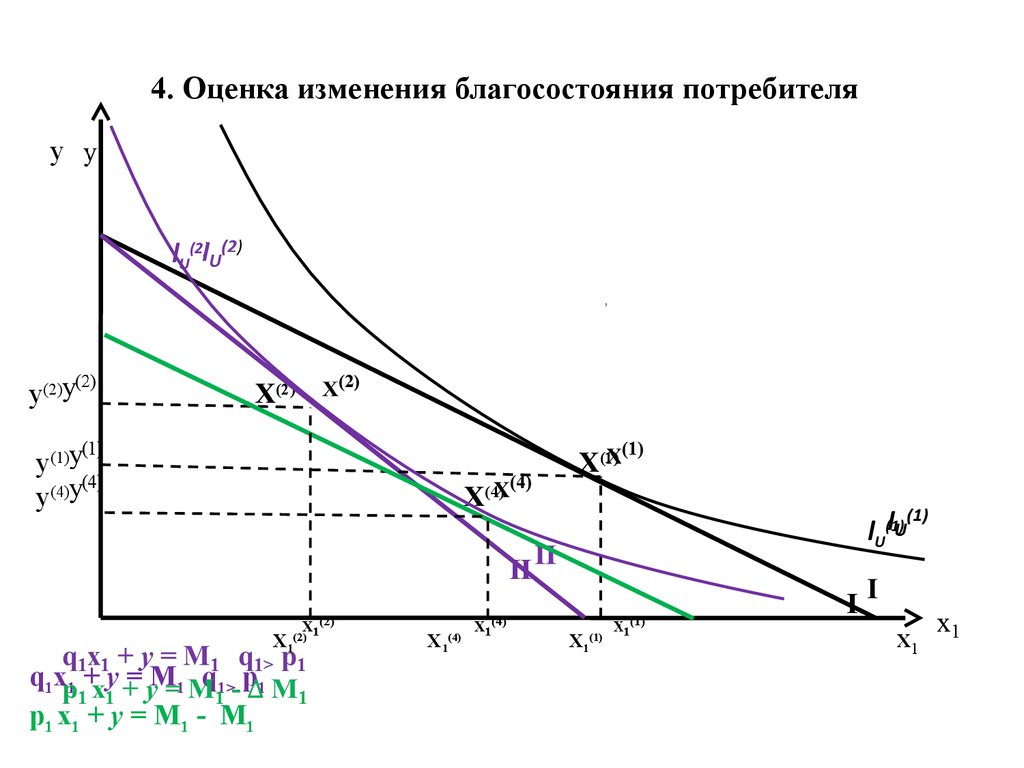
22. 4. Оценка изменения благосостояния потребителя

y
lU(2)
y(2)
X(2)
y(1)
y(4)
X(1)
X(4)
lU(1)
II
I
X1(2)
q1x1 + y = M1 q1> p1
p1 x1 + y = M 1 - M 1
X1(4)
X1(1)
x1

23. 5. Теория выявленных предпочтений

Основные предпосылки теории выявленных предпочтений:
1. Отказ от использования понятия полезности и функции полезности.
2. Отношение предпочтения связано с рыночной ситуацией.
Рыночная ситуация – пара, состоящая из вектора цен и дохода.
3. Потребитель, приобретая на рынке потребительский набор
обязательно тратит весь свой доход.
4.Выбор потребителя является единственным, (предпосылка о строгой
выпуклости предпочтений потребителя).
5.Если выбран потребительский набор x1, то он определяет
единственным образом рыночную ситуацию, т.е. x1 ⇒ ( γp1,γM1) так, что
γp1x1 = γ M1.

24. 5. Теория выявленных предпочтений

Потребительский набор x1 = ( …) прямо выявленно (т.е. явно )
предпочитается потребительскому набору x2 = ( …), если p1x1 ≥ p1x2, где
p1x1 = M1 и ( p1,M1) – некоторая (вполне определенная) рыночная
ситуация.
Символика x1 x2.
Слабая аксиома выявленных предпочтений ( СлАВП):
если x1 x2 и x1 ≠ x2, то неверно, что x2 x2.
Сильная аксиома выявленных предпочтений ( СиАВП):
если x1 x2 , x2 x3, …, xk-1xk и x1 ≠ xk, то неверно, что xk x1.
СлАВП есть при СиАВП k=2.

25. 5. Теория выявленных предпочтений

Если отказаться от предпосылки о строгой выпуклости предпочтений
потребителя, оставив предпосылку о выпуклости предпочтений
потребителя, то от СиАВП можно перейти к к обобщенной аксиоме
выявленных предпочтений (ОбАВП)
Обобщенная аксиома выявленных предпочтений (ОбАВП):
если x1 xk и x1 ≠ xk, то неверно, что xk x1.
Теорема Эфриата
Для того чтобы данные о потребительском поведении индивидуума
соответствовали ОбАВП, необходимо и достаточно, чтобы в основе
потребительского поведения лежали рациональные предпочтения.