Похожие презентации:
Правильные многоугольники
1.
ПРАВИЛЬНЫЕМНОГОУГОЛЬНИКИ
2. Из истории
•Правильные многоугольники были известны еще в глубокойдревности. В египетских и вавилонских старинных
памятниках встречаются правильные четырехугольники,
шестиугольники и восьмиугольники в виде изображений на
стенах и украшений, высеченных из камня.
•Древнегреческие ученые стали проявлять большой интерес к
правильным многоугольникам еще со времен Пифагора.
•Учение о правильных многоугольниках было
систематизировано и изложено в 4 книге «Начал» Евклида.
3.
ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИКПравильным многоугольником называется
выпуклый многоугольник, у которого все
углы равны и все стороны равны.
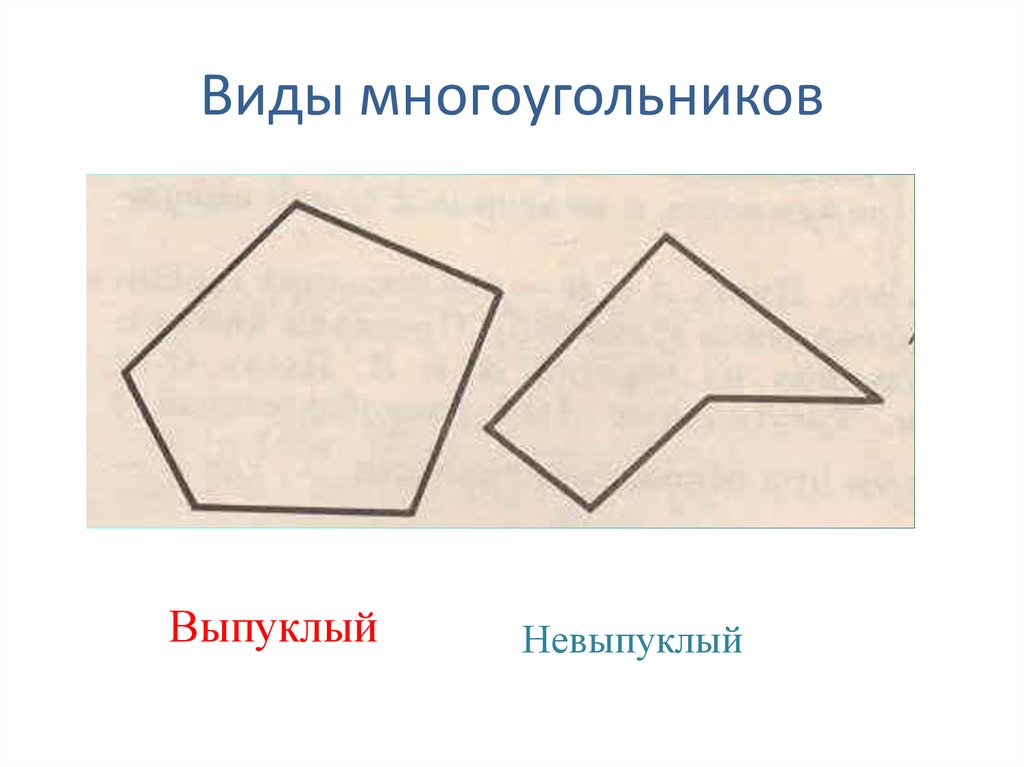
4. Виды многоугольников
ВыпуклыйНевыпуклый
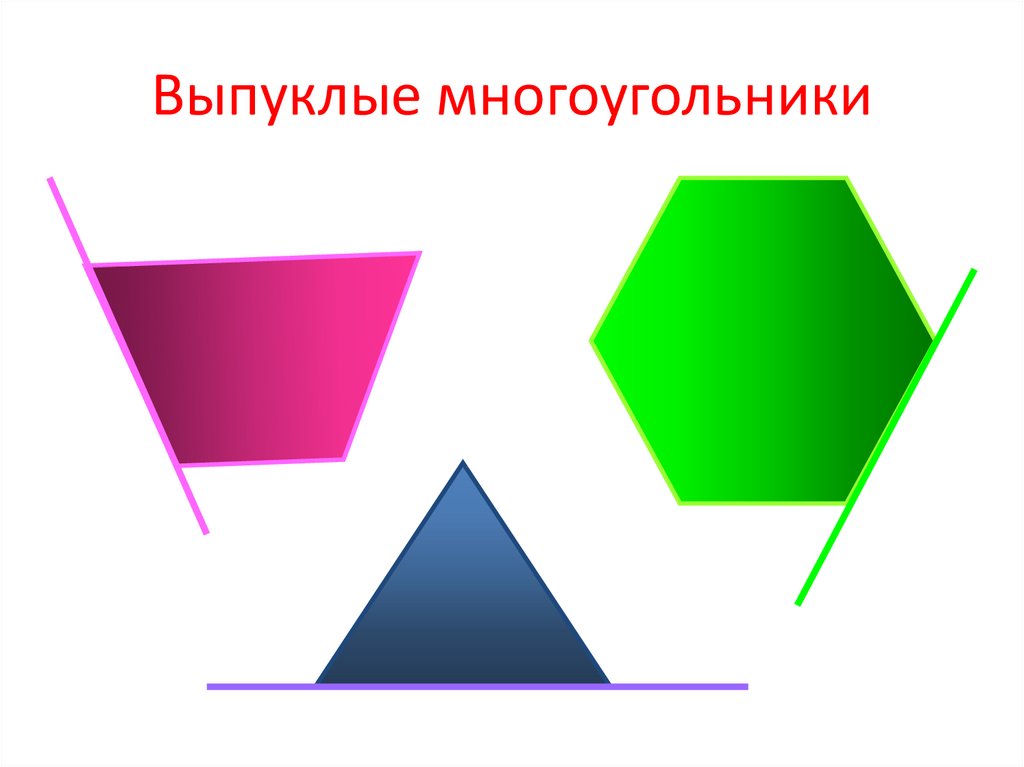
5. Выпуклые многоугольники
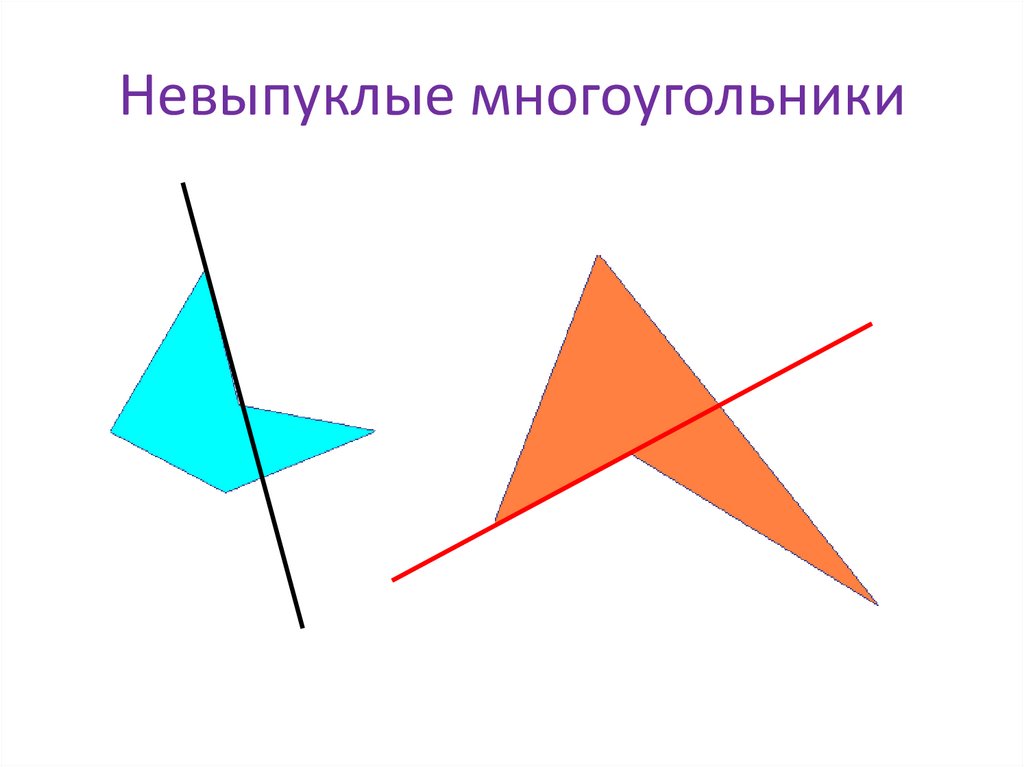
6. Невыпуклые многоугольники
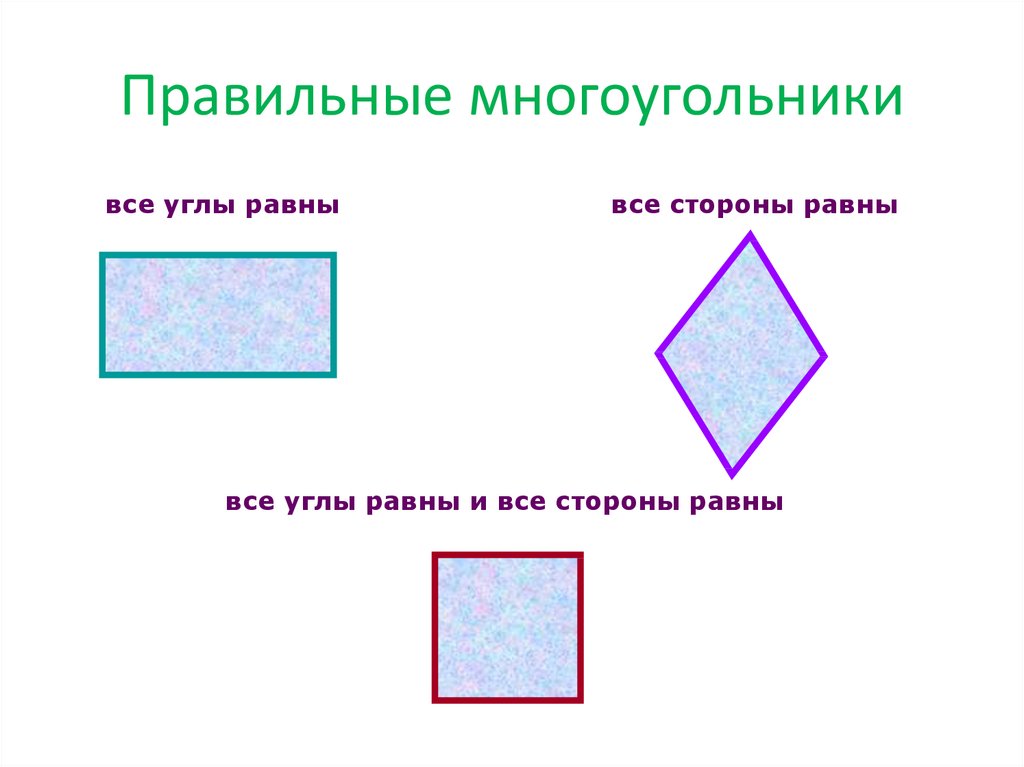
7. Правильные многоугольники
все углы равнывсе стороны равны
все углы равны и все стороны равны
8.
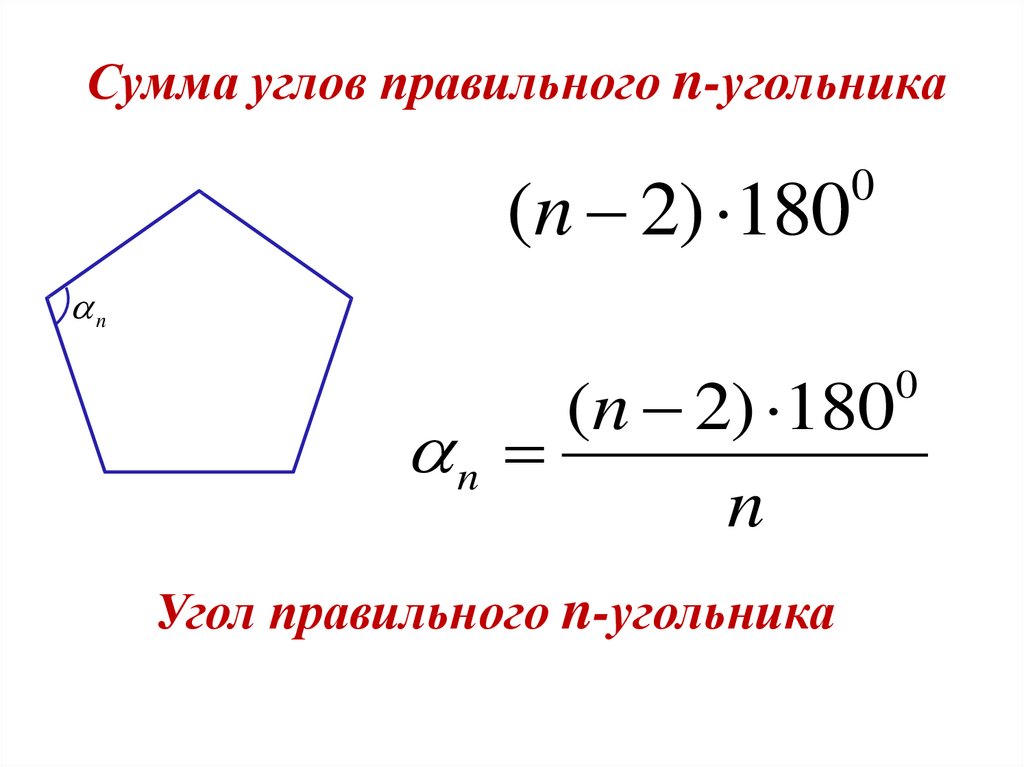
Сумма углов правильного n-угольника(n 2) 180
0
n
(n 2) 180
n
n
Угол правильного n-угольника
0
9. Решаем задания №1
10.
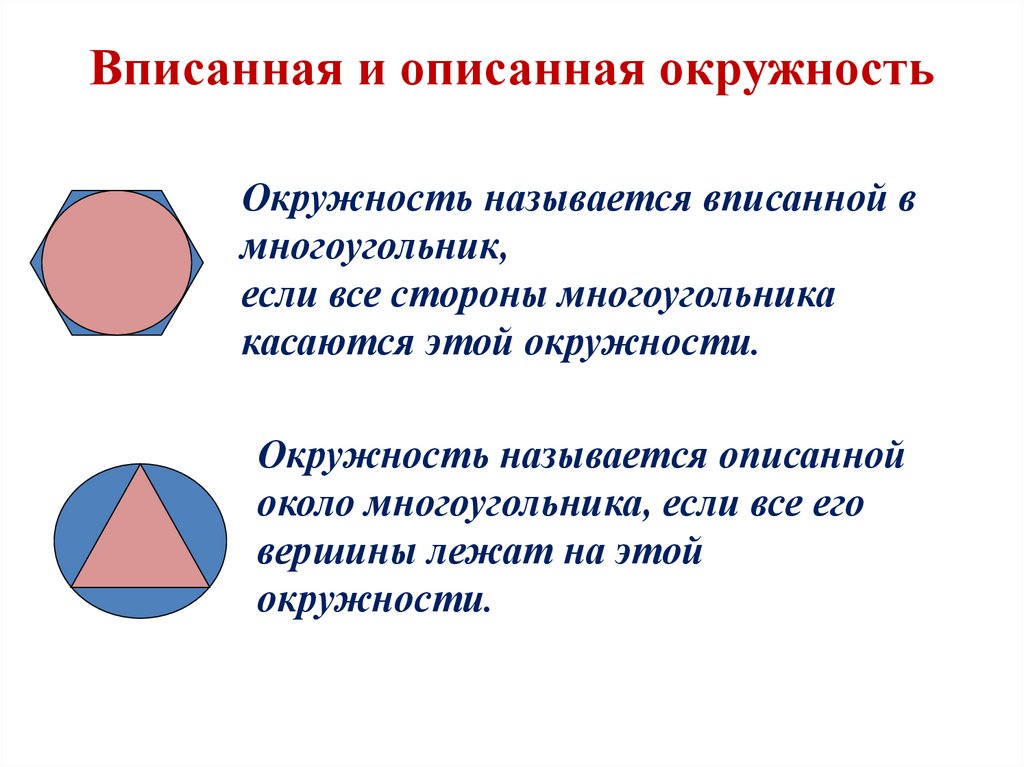
Вписанная и описанная окружностьОкружность называется вписанной в
многоугольник,
если все стороны многоугольника
касаются этой окружности.
Окружность называется описанной
около многоугольника, если все его
вершины лежат на этой
окружности.
11.
Вписанная и описанная окружностьОкружность, вписанная в
правильный многоугольник,
касается сторон многоугольника
в их серединах.
Центр окружности, описанной
около правильного многоугольника,
совпадает с центром окружности,
вписанной в тот же многоугольник.
12.
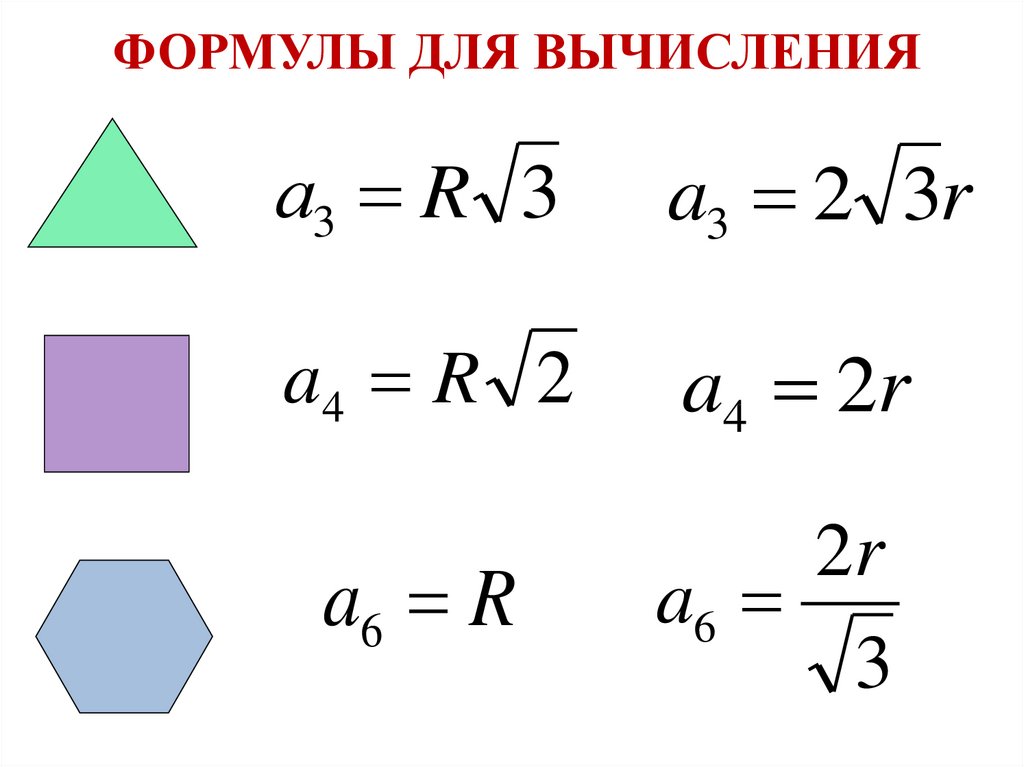
ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯПлощадь правильного многоугольника
1
S
Pr
2
Сторона правильного многоугольника
180
an 2 R sin
n
0
Радиус вписанной окружности
180
r R cos
n
0
13.
Группа 1Дано: R, n=3
Найти: а
Группа 2
Дано: R, n=4
Найти: а
Группа 3
Дано: R, n=6
Найти: а
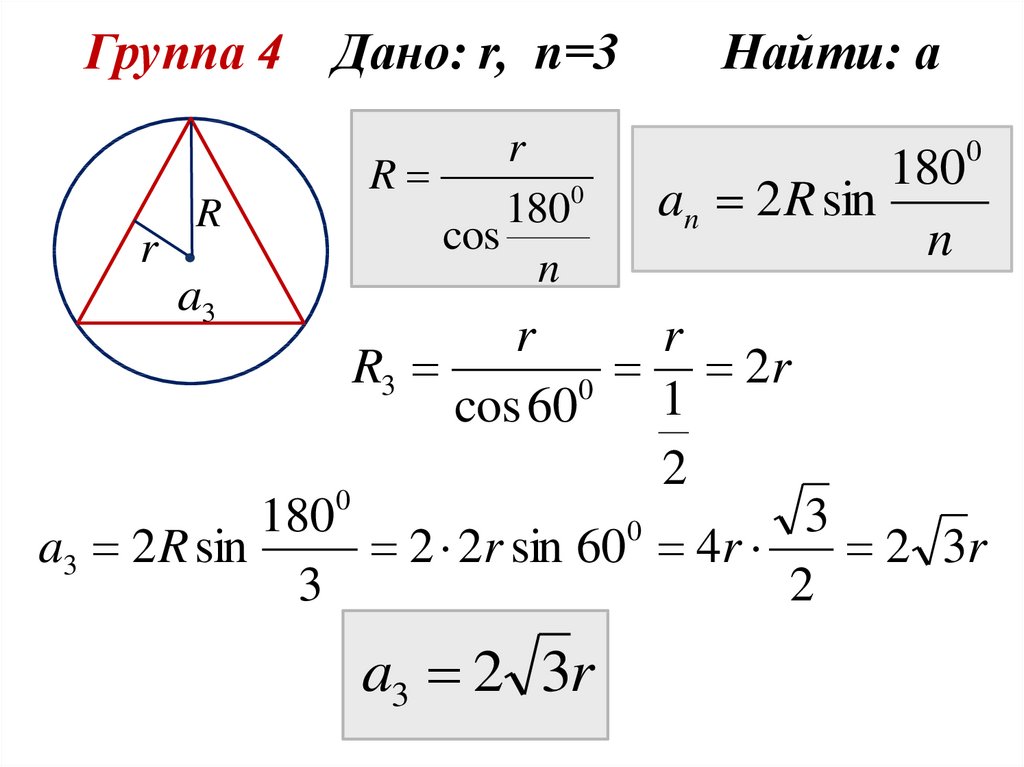
Группа 4 Дано: r, n=3
Найти: а
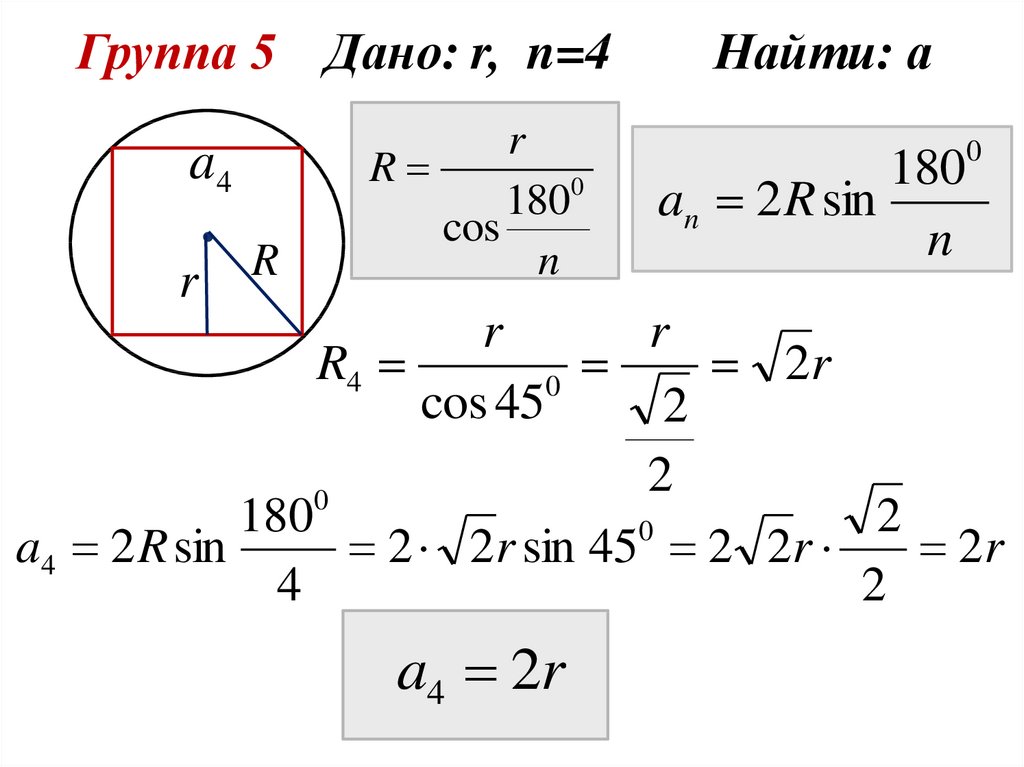
Группа 5 Дано: r, n=4
Найти: а
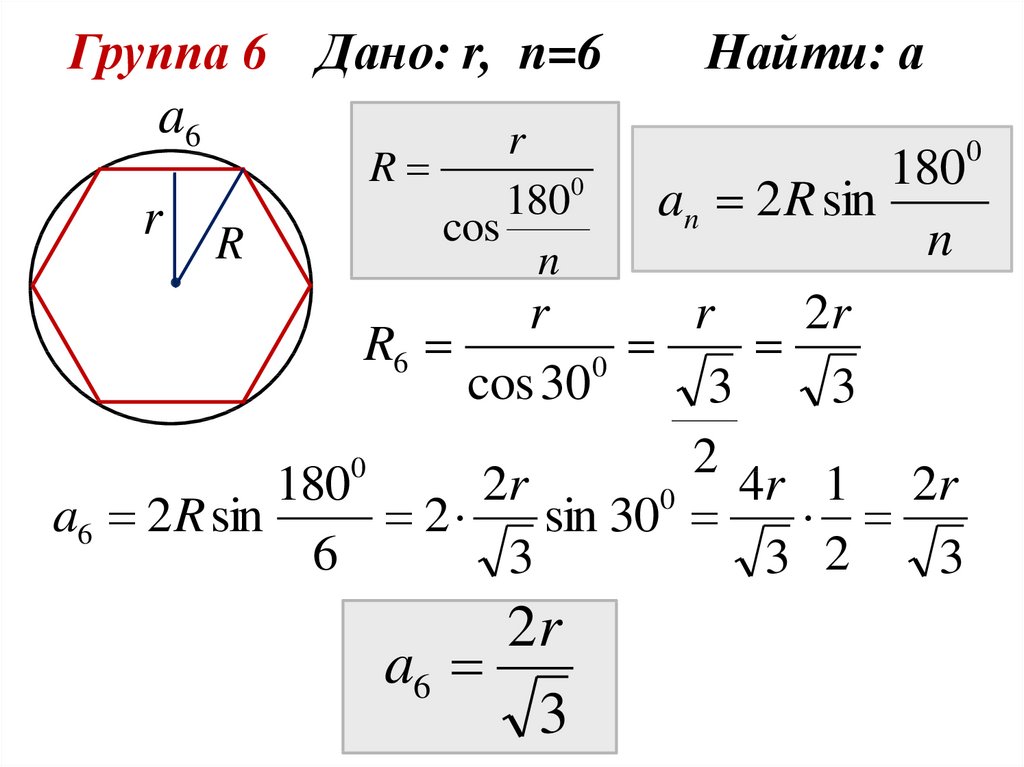
Группа 6
Найти: а
Дано: r, n=6
14.
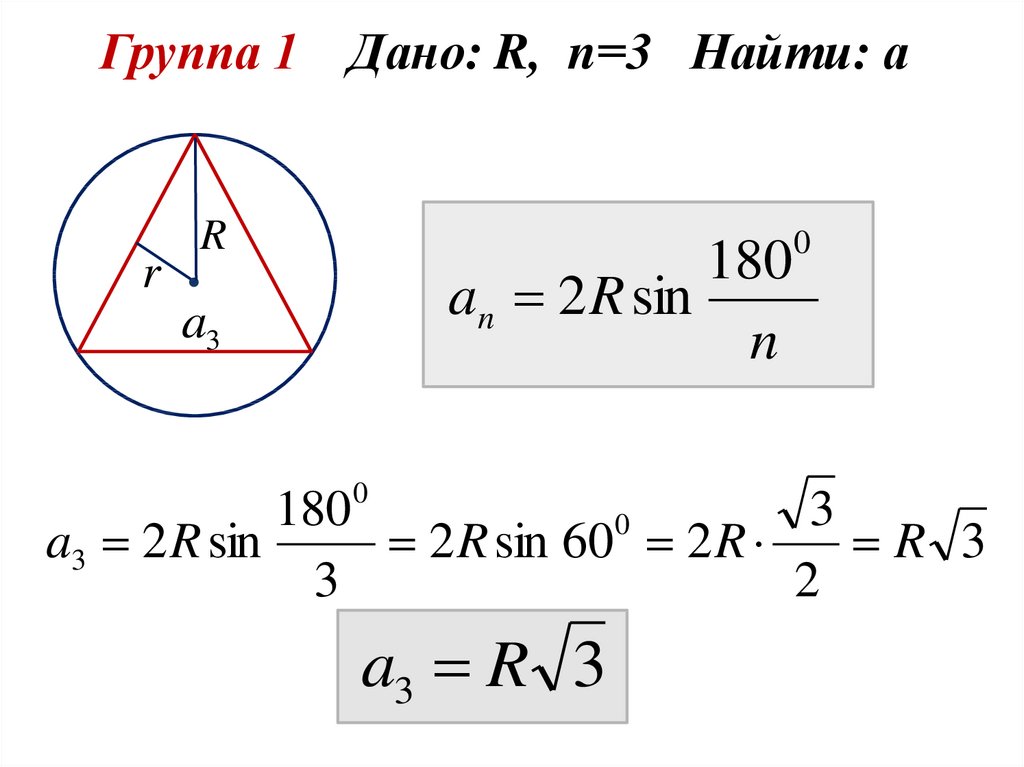
Группа 1 Дано: R, n=3 Найти: аr
R
180
an 2 R sin
n
a3
0
0
180
3
0
a3 2 R sin
2 R sin 60 2 R
R 3
3
2
a3 R 3
15.
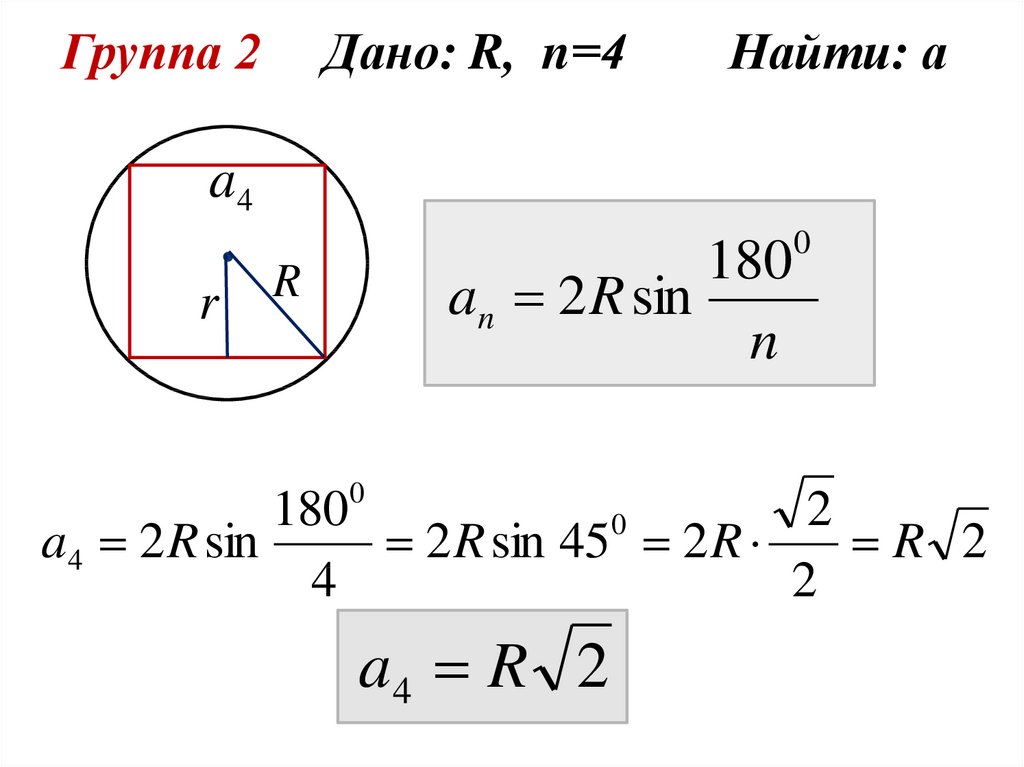
Группа 2Дано: R, n=4
Найти: а
a4
r
180
an 2 R sin
n
R
0
0
180
2
0
a4 2 R sin
2 R sin 45 2 R
R 2
4
2
a4 R 2
16.
Группа 3 Дано: R, n=6Найти: а
a6
r
R
180
an 2 R sin
n
0
0
180
1
0
a6 2 R sin
2 R sin 30 2 R R
6
2
a6 R
17.
Группа 4 Дано: r, n=3r
r
R
0
180
cos
n
R
a3
0
Найти: а
180
an 2 R sin
n
0
r
r
R3
2r
0
1
cos 60
2
180
3
0
a3 2 R sin
2 2r sin 60 4r
2 3r
3
2
a3 2 3r
18.
Группа 5 Дано: r, n=4a4
r
R
r
R
1800
cos
n
Найти: а
180
an 2 R sin
n
0
r
r
R4
2r
0
cos 45
2
2
0
180
2
0
a4 2 R sin
2 2r sin 45 2 2r
2r
4
2
a4 2r
19.
Группа 6 Дано: r, n=6a6
r
R
1800
cos
n
Найти: а
180
an 2 R sin
r R
n
r
r
2r
R6
0
cos 30
3
3
2
0
180
2r
4r 1 2r
0
a6 2R sin
2
sin 30
6
3
3 2
3
2r
a6
3
0
20.
ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯа3 R 3
a3 2 3r
a4 R 2
a4 2r
a6 R
2r
a6
3
21.
Подведем итогМы знаем формулы:
180
an 2 R sin
n
180
r R cos
n
1
S
Pr
2
0
0
а3 R 3 a3 2 3r
a4 R 2 a4 2r
a6 R
2r
a6
3
22.
23. Решаем задания №3
24. Паркеты из правильных многоугольников
• В математике паркетом называют«замощение» плоскости
повторяющимися фигурами без
пропусков и перекрытий.
Простейшие паркеты были
открыты пифагорейцами около
2500 лет тому назад.
Они установили, что вокруг одной точки могут лежать либо шесть
правильных многоугольников (3600: 600 = 6), либо четыре
квадрата (3600: 900 = 4), либо три правильных шестиугольника
(3600: 1200 = 3), так как сумма углов с вершиной этой точки равна
3600.
25.
26. ПАРКЕТЫ ИЗ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ
Паркеты из одинаковых правильныхмногоугольников
Паркеты из разных правильных многоугольников
27.
28.
29.
30. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ
Правильные многоугольникивстречаются в природе. Один
из примеров – это пчелиные
соты, которые представляют
собой прямоугольник,
покрытый правильными
шестиугольниками. На этих
шестиугольниках пчелы
выращивают из воска ячейки,
представляющие собой
прямые шестиугольные
призмы. В них пчелы и
откладывают мед, а затем
снова покрывают сплошным
прямоугольником из воска.
31. Правильные многоугольники в природе
Почему пчелы «выбрали» себе для ячеек на сотахформу правильного шестиугольника?
Строя шестиугольные ячейки пчелы наиболее
экономно используют площадь внутри небольшого
улья и воск для изготовления ячеек.
Причем пчелиные соты представляют собой не
плоский, а пространственный паркет, поскольку
заполняют пространство так, что не остается
просветов.
И как не согласиться с мнением пчелы из сказки
«Тысяча и одна ночь»: «Мой дом построен по законам
самой строгой архитектуры. Сам Евклид мог бы
поучиться, познавая геометрию моих сот».
32. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ
Многие простейшиеморские организмы
( радиолярии )
имеют форму
правильных
многоугольников
33. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ
Снежинки имеютформу правильных
многоугольников
34.
35.
36. В мире растений правильные многоугольники тоже встречаются, но гораздо реже.
37. Эти удивительные правильные многоугольники
38. Мне понравился урок и я узнал много интересного. Мне понравился урок, но я испытывал затруднения. Мне не понравился урок.
Мне понравился урок и я узнал много интересного.Мне понравился урок, но я испытывал затруднения.
Мне не понравился урок.


























 Математика
Математика








