Modely časových řad

1. Modely časových řad

2. Modelování časových řad

Klasická analýza časových řad vychází z předpokladu,
že časovou řadu je možné rozdělit na tři složky:
Trend (Tt)
Periodickou složku (Pt)
Náhodná složka (εt)

3. Modelování časových řad

Dekompozice časové řady
Aditivní model
y t Tt Pt t
t = 1,2,…,n
Multiplikativní model
y Tt P t t
´
t
t = 1,2,…,n

4. Modelování časových řad

Neperiodické časové řady
Bez periodické složky
Periodické časové řady
Obsahují periodickou složku

5. Analýza neperiodických ČŘ

Hlavním úkolem analýzy neperiodických ČŘ je
vystižení základní tendence jejich vývoje – trendu.
Popis trendu (trendové složky) v časových řadách:
Graficky;
Mechanicky (pomocí klouzavých průměrů);
Analyticky (pomocí trendových funkcí).

6. Klouzavé průměry

Vyrovnání pomocí klouzavých průměrů spočívá v
nahrazení skutečných hodnot ČŘ průměrem z
určitého počtu hodnot. Trend v krátkých časových
úsecích
odhadujeme
průměrem
několika
sousedních pozorování.

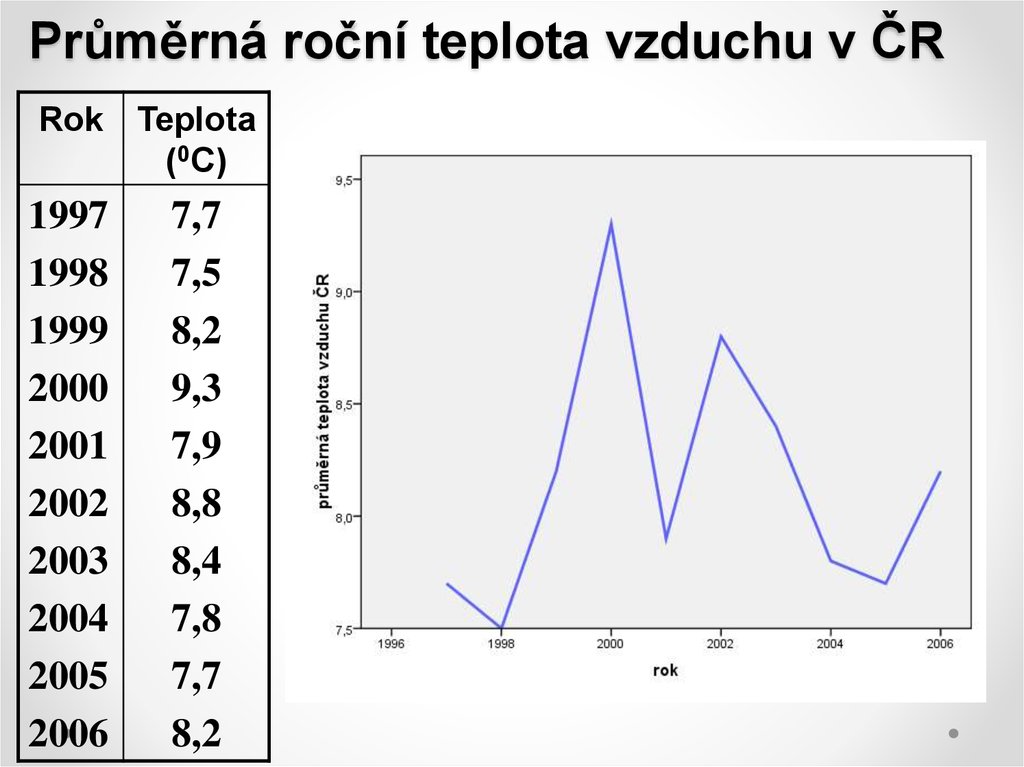
7. Průměrná roční teplota vzduchu v ČR

Rok Teplota
(0C)
1997
1998
1999
2000
2001
2002
2003
2004
2005
2006
7,7
7,5
8,2
9,3
7,9
8,8
8,4
7,8
7,7
8,2

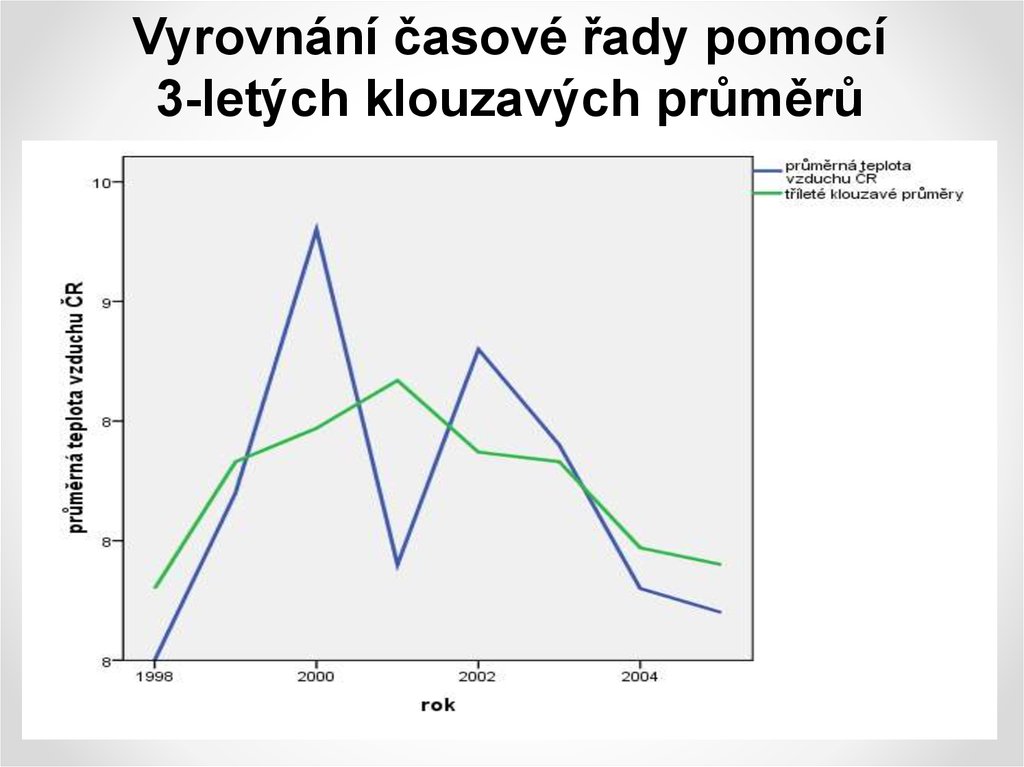
8. Vyrovnání časové řady pomocí 3-letých klouzavých průměrů

9. Vyrovnání časové řady pomocí 3-letých a 5-letých klouzavých průměrů

10. Centrované klouzavé průměry

Rok/čt
yt
2005/I
II
III
IV
2006/I
II
III
IV
2
4
5
3
3
5
6
4
k=4
3,50
3,75
4,00
4,25
4,5
Centrované klouzavé
průměry
3,625
3,875
4,125
4,375

11. Trendové funkce

Vyrovnání pomocí trendových funkcí
Jde o vyjádření průběhu ČŘ matematickou funkcí,
kde zkoumaný ukazatel ČŘ vystupuje jako závisle
proměnná yt a čas (časová proměnná) jako
nezávisle proměnná t.

12. Trendové funkce

Těmto vlastnostem odpovídají zejména tyto křivky:
Lineární
Tt = a + b· t
Kvadratická
Tt = a + b· t + c· t2
Logaritmická
Tt = a + b· log t
Exponenciální
Tt = a · bt
Mocninná
Tt = a · tb
Odmocninná
Tt a b t

13. Adaptivní modely časových řad

Trendová složka časové řady není konstantní, ale
mění se v čase, proto není možné k jejímu popisu
použít jednu matematickou funkci s konstantními
parametry.

14. Adaptivní modely časových řad

Adaptivní modely vychází z předpokladu, že pro
konstrukci extrapolační prognózy budoucího
vývoje mají cenu nejnovější pozorování časové
řady.
Adaptivní modely tedy berou v úvahu
„stárnutí“ informací.

15. Adaptivní modely časových řad

Skupina adaptivních modelů je rozsáhlá.
Jedny z nejčastěji používaných metod, které
přináší v praktických aplikacích dobré výsledky,
jsou metody exponenciálního vyrovnávání.

16. Metody exponenciálního vyrovnávání

Jednoduché exponenciální vyrovnávání trend
v krátkých úsecích konstantní, jeden parametr α.
Brownovo exponenciální vyrovnávání úroveň
a trend řady, dva parametry.
Holtovo exponenciální vyrovnávání úroveň
a trend řady, dva parametry α, γ.
Exponenciální vyrovnání s tlumeným trendem
tři parametry α, γ, φ.

17. Adaptivní modely časových řad

Nejjednodušším případem je jednoduché
exponenciální vyrovnání.
Odhad trendu v čase t
yˆ t yt (1 ) yˆ t 1
α . . . vyrovnávací konstanta, 0 < α < 1

18. α = 0,4

Rok Inflace
94
10,9
95
96
97
98
99
00
01
02
03
04
9,1
8,8
8,5
10,7
2,1
3,9
4,7
1,8
0,1
2,8
yˆ t
9,6
9,4
Míra inflace vyjádřená přírůstkem
průměrného ročního indexu
spotřebitelských cen
yˆ t yt (1 ) yˆ t 1
α = 0,4
y1 y 2 y 3
yˆ 1
9,6
3
yˆ 2 0,4 9,1 0,6 9,6 9,4

19. Posouzení vhodnosti modelů ČŘ

Často používaným ukazatelem, který
slouží k popisu stupně shody je index
determinace I2
y y
n
I 1
2
t 1
n
t
t
y y
t 1
t
2
2

20. Posouzení vhodnosti modelů ČŘ

Moderní statistická metodologie standardně
implementovaná v statistických programech.
M.E. – střední chyba odhadu
M.S.E. – střední kvadratická chyba odhadu
M.A.E. střední absolutní chyba odhadu
M.P.E. – střední chyba odhadu
M.A.P.E. – střední absolutní procentní chyba odhadu
y t y
100
MAPE
n
yt

21. Analýza periodických ČŘ

Periodická složka:
• ≤ 1 rok
…
sezónní složka Si
• > 1 rok
…
cyklická složka Ci

22. Sezónní kolísání

Vždy je potřeba identifikovat, zda je sezonní
kolísání skutečně statisticky významné;
(grafická analýza, výpočet klouzavých průměrů,
autokorelační funkce, analýza periodogramu).

23. Popis sezónní složky

Aditivní model
Sezónní složka je v tomto případě vyjádřena
pomocí sezónních odchylek;
i yi y
i yi yi
Součet sezónních odchylek = 0

24. Popis sezónní složky

Multiplikativní model
Sezónní složka je vyjádřena pomocí sezónních
indexů.
skuteč . hodnota řady
st
vyrovnaná hodnota řady

25. Popis sezónní složky

Aritmetický průměr y skutečných hodnot za období
celé periody sezónního cyklu (průměrný údaj,
připadající na jedno období v rámci zkoumaného
roku).
Vyrovnané hodnoty yi stanovené buď pomocí
klouzavých průměrů nebo některou z metodou
analytického vyrovnání (hodnoty vypočítané na
základě trendové funkce).
.

26. Sezónní očišťování

Sezónní očišťování časové řady zbavuje časovou
řadu periodického kolísání, které by mohlo maskovat
charakter trendu řady.
Používá se jako předběžný stupeň před analýzou
trendu časové řady.

27. Náhodná složka

Náhodné (nesystematické) složky tzv. rezidua. –
chápeme jako výsledky působení určitých blíže
nespecifikovaných (stochastických) náhodných vlivů.
Náhodnou složku i vyjadřujeme ve tvaru
i yi yi

28. Náhodná složka

Střední hodnota náhodné složky i se rovná nule.
Variabilita náhodných složek i se v čase nemění
rozptyl je konstantní.
Jednotlivé hodnoty náhodné složky i jsou vzájemně
lineárně nezávislé (nekorelované).
Jsou-li tyto předpoklady splněny, tvoří řada i tzv.
bílý šum.

29. Předpovědi časových řad

Interpolace
Extrapolace

30. Předpovědi časových řad

Bodová předpověď
yi k
Intervalová předpověď
P ui k un k ui k 1 ,
kde i je pořadové číslo časové proměnné v
časové řadě o n členech, k-počet kroků
dopředu.

31. Předpovědi časových řad

Každá předpověď je spojena s určitou chybou
předpovědi. Případná chyba je tím větší, čím kratší
je délka časové řady, čím nedokonalejší je popis
uplynulého vývoje a čím vzdálenější je horizont
předpovědi.

32. Hodnocení přesnosti prognóz

Pseudoprognóza se konstruuje tak, že
k vyrovnání časové řady se nevyužije několik
posledních hodnot řady, které jsou tak jako by
„předpovídanými“ hodnotami.
Pro změření kvality skutečných předpovědí
i pseudopředpovědí se používá Theilův
koeficient nesouladu TH2 .

33. Hodnocení přesnosti prognóz

Relativní chyba extrapolace (%) TH
0 % < TH < 5% chyba predikce malá
5 % < TH < 10 % chyba predikce střední
10 % < TH
chyba predikce velká,
model pro predikci nepoužívat
Relativní chyba prognózy (predikce) Pt