Похожие презентации:
Časové řady
1. Časové řady
2. Časová řada
Časová řada = posloupnost v čase seřazenýchúdajů, zpravidla ve směru minulost přítomnost.
Analýza časových řad soubor metod, které
slouží k:
o popisu dynamiku vývoje sledovaných jevů
v referenčním období (tj. období, kterého se to
týká),
o prognózování budoucího vývoje
3. Základní druhy časových řad
Podle rozhodného časového hlediskaIntervalové časové řady
Okamžikové časové řady
4. Základní druhy časových řad
Podle periodicity sledováníKrátkodobé (týdenní, měsíční, čtvrtletní)
Dlouhodobé (roční, víceleté)
Podle druhu sledovaných ukazatelů
ČŘ primárních ukazatelů – tj. ukazatelů prvotních
ČŘ sekundárních ukazatelů – tj. ukazatelů
odvozených (součtové, průměrné nebo poměrové)
Podle způsobu vyjádření údajů
ČŘ naturálních ukazatelů
ČŘ peněžních ukazatelů
5. Srovnatelnost údajů v ČŘ
Srovnatelnost údajů v ČŘKaždá ČŘ musí splňovat 3 hlediska srovnatelnosti:
Hledisko věcné srovnatelnosti
Hledisko prostorové srovnatelnosti
Hledisko časové srovnatelnosti
6. Elementární charakteristiky ČŘ
Elementární charakteristiky je možné rozčlenit:1) Na ukazatele, které posuzují úrovně ČŘ.
2) Na ukazatele, které charakterizují dynamiku
(rychlost změn) vývoje ČŘ.
7. Ukazatele posouzení úrovně ČŘ
Úroveň hodnot časové řady ve sledovaném obdobícharakterizujeme pomocí průměru řady.
Intervalové časové řady
Aritmetický průměr
y
y
n
i
8. Ukazatele posouzení úrovně ČŘ
Zajištění srovnatelnosti se provdání přepočítánímočištěním časové řady od kalendářních variací.
y
(o)
t
kt
yt
kt
, t 1, 2 , , n
yt .....
původní hodnota ČŘ;
kt .....
průměrný počet dní v dílčím období
kt .....
počet dní v dílčím období (měsíc, čtvrtletí);
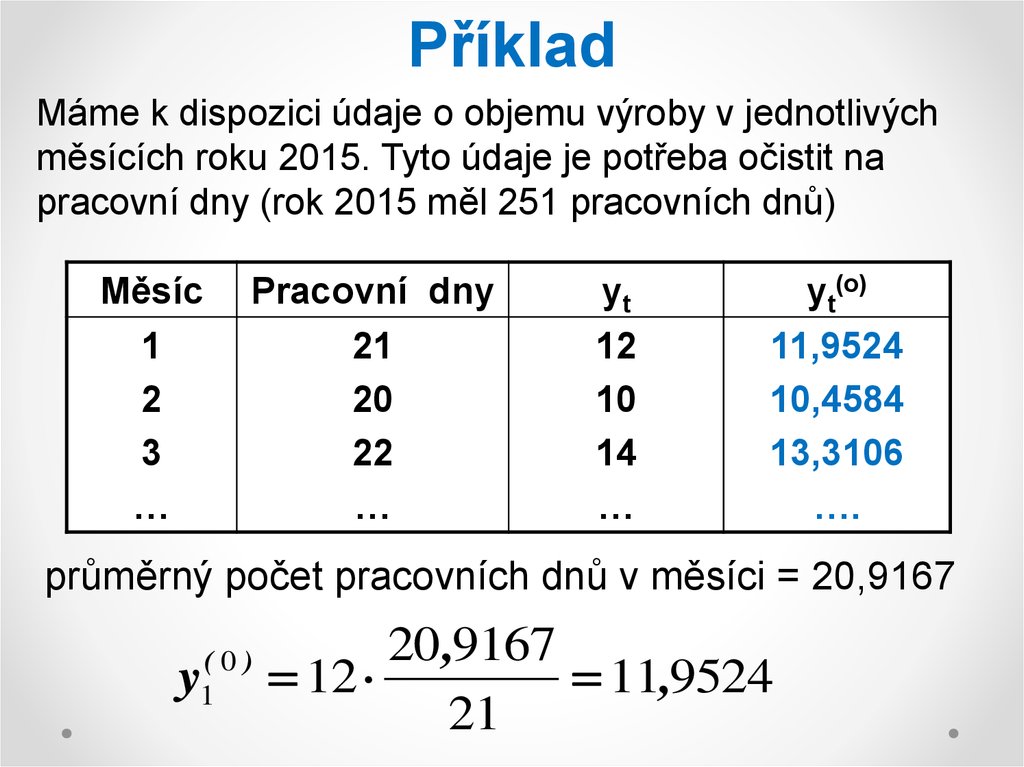
9. Příklad
Máme k dispozici údaje o objemu výroby v jednotlivýchměsících roku 2015. Tyto údaje je potřeba očistit na
pracovní dny (rok 2015 měl 251 pracovních dnů)
Měsíc
1
2
3
…
Pracovní dny
21
20
22
…
yt
12
10
14
…
yt(o)
11,9524
10,4584
13,3106
….
průměrný počet pracovních dnů v měsíci = 20,9167
(0)
1
y
20 ,9167
12
11,9524
21
10. Ukazatele posouzení úrovně ČŘ
Okamžikové časové řadyChronologický průměr prostý
1
1
y1 y2 yn 1 yn
2
y 2
n 1
Vzorec vyjadřuje prostou formu chronologického
průměru za předpokladu, že délka mezi jednotlivými
časovými okamžiky je stejná.
11. Ukazatele posouzení úrovně ČŘ
Okamžikové časové řadyChronologický průměr vážený
Není-li délka mezi jednotlivými časovými okamžiky
konstantní, je nutné jednotlivé dílčí průměry vážit
délkami příslušných intervalů.
y 2 y3
yn 1 yn
y1 y2
t 2 t1
t3 t 2
t n t n 1
2
2
y 2
t n t1
12. Příklad
K dispozici máme údaje o počtu práce neschopnýchzaměstnanců ve výrobním podniku v prvním čtvrtletí
roku 2015. Na základě údajů vedených v následující
tabulce vypočítejte průměrný stav práce
neschopných pracovníků podniku za období od 1.1.
do 1.4. 2015.
Následně uvedená časová řada je okamžiková,
protože rozhodným okamžikem sledování je vždy
první den daného měsíce. Protože vzdálenost mezi
jednotlivými okamžiky sledování není stejná,
použijeme pro výpočet vážený chronologický průměr.
13.
DatumPočet práce
neschopných
1.1.
25
1.2.
1.3.
yi
y1
25 26
25 ,5
y2
26 18
22
26
18
1.4.
27
Součet
x
2
y3
ti délka
intervalu
yi t i
31
790,5
28
616
31
697,5
90
2104
2
18 27 22 ,5
2
2104
y
23,37 24
90
14. Ukazatele dynamiky vývoje ČŘ
Absolutní charakteristikyPrvní absolutní diference.
d yt yt 1
1
yt
t = 2, 3, ….., n.
Druhá absolutní diference.
d d d
2
yt
1
yt
1
yt 1
t = 3, 4, …., n.
15. Ukazatele dynamiky vývoje ČŘ
Absolutní charakteristikySouhrnnou absolutní charakteristikou je průměrný
absolutní přírůstek (resp. úbytek) hodnoty
ukazatele ČŘ.
( y2 y1 ) ( y3 y2 ) ( yn yn 1 ) yn y1
d
n 1
n 1
16. Ukazatele dynamiky vývoje ČŘ
Relativní charakteristikyKoeficient růstu.Vyjádřený v % se nazývá tempem
růstu.
yt
kt
, t 2 , 3,...,n
yt 1
Průměrný koeficient růstu
k
n 1
k1 k2 ...... kn 1
n 1 yn
y1
17. Ukazatele dynamiky vývoje ČŘ
Tempo přírůstkud
yt yt 1
rt
yt 1
yt 1
1
t
Koeficienty zrychlení
2
t
1
t 1
d
zt
d
Bazický index
yt
BI t
y0
18. Příklad
Máme k dispozici údaje o roční spotřebě chleba v kgna jednoho obyvatele v letech 2005 - 2014.
Pomocí elementárních charakteristik popište
dynamiku vývoje sledovaného ukazatele.
kg/obyvatel/rok
60,0
50,0
40,0
30,0
20,0
10,0
0,0
2005 2006 2007 2008 2009 2010 2011 2012 2013 2014
rok
19. Příklad
Spotřeba chleba v kg na obyvatele za rokrok
yt
d1yt
d2yt
rt
kt
BI2005
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
51,3
49,5
50,3
44,1
43,4
40,9
42,4
41,3
39,3
40,0
-1,8
0,8
-6,2
-0,7
-2,5
1,5
-1,2
-2,0
0,7
2,6
-7,0
5,5
-1,9
.
.
.
.
-0,035
0,016
-0,123
-0,015
-0,058
.
.
.
.
0,965
1,016
0,877
0,985
0,942
1,037
0,973
0,96
0,98
0,86
0,85
.
.
.
.
.
20. Příklad
yy
n
k
i
442 ,5
44 ,25
10
n 1 yn
y1
9
40
0 ,9727
51,3
yn y1 40 51,3
d
1,2556
n 1
9
21. Modely časových řad
22. Modelování časových řad
Klasická analýza časových řad vychází z předpokladu,že časovou řadu je možné rozdělit na tři složky:
Trend (Tt)
Periodickou složku (Pt)
Náhodné kolísání (εt)
23. Modelování časových řad
Dekompozice časové řadyAditivní model
y t Tt Pt t
t = 1,2,…,n
Multiplikativní model
y Tt P t t
´
t
t = 1,2,…,n
24. Modelování časových řad
Neperiodické časové řadyBez periodické složky
Periodické časové řady
Obsahují periodickou složku























 Математика
Математика






