Indexní analýza

1. Indexní analýza

2. Indexní analýza

Hodnoty ukazatelů porovnáváme pomocí
rozdílu a podílu.
Absolutní změna - rozdíl hodnot ukazatele
absolutní přírůstek
Relativní změna – podíl hodnot ukazatele
index

3. Elementární srovnávání ukazatelů

Indexy bázické - jsou vztaženy k pevně zvolenému
období (bázi)
qi
Ii / 0
q0
Absolutní přírůstek
i . . . běžné období
0 . . . základní období
Δ = qi – q0

4. Elementární srovnávání ukazatelů

Indexy řetězové - jsou vztaženy k předcházejícímu
období (koeficient růstu k)
qi
I i / i 1
qi 1
Absolutní přírůstek
i . . . běžné období
i -1 . . . předcházející období
Δ = qi – qi-1

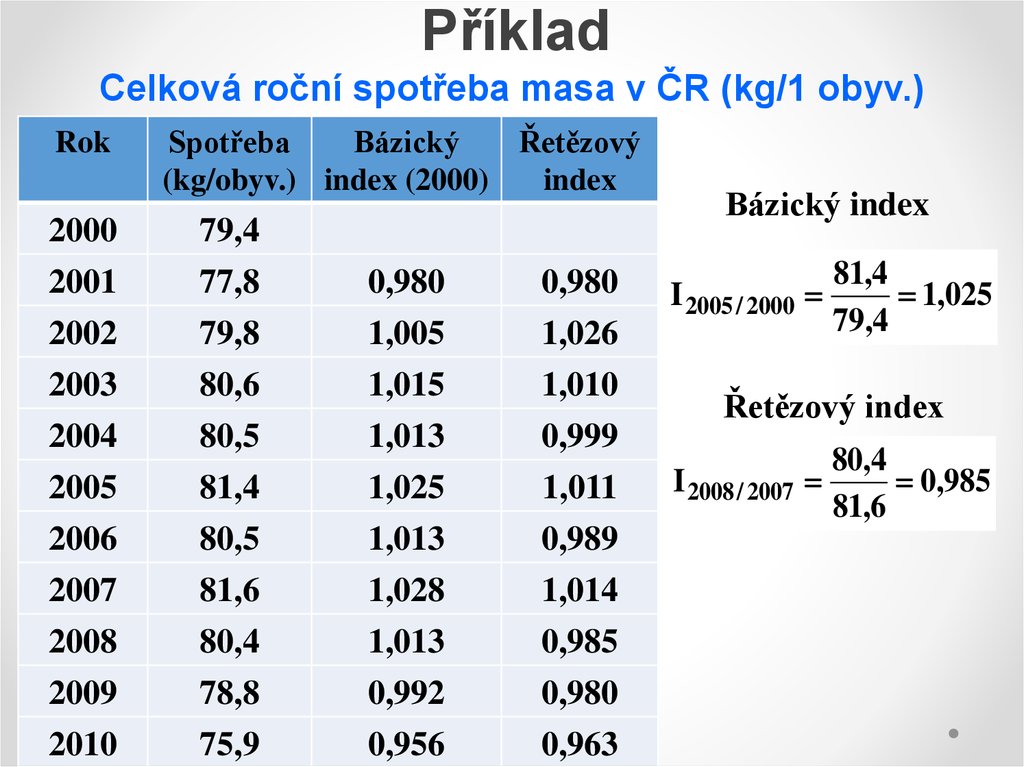
5. Příklad

Celková roční spotřeba masa v ČR (kg/1 obyv.)
Rok
Spotřeba
Bázický
Řetězový
(kg/obyv.) index (2000)
index
2000
2001
79,4
77,8
0,980
0,980
2002
2003
2004
2005
79,8
80,6
80,5
81,4
1,005
1,015
1,013
1,025
1,026
1,010
0,999
1,011
2006
2007
80,5
81,6
1,013
1,028
0,989
1,014
2008
2009
80,4
78,8
1,013
0,992
0,985
0,980
2010
75,9
0,956
0,963
Bázický index
I 2005 / 2000
81,4
1,025
79,4
Řetězový index
I 2008 / 2007
80,4
0,985
81,6

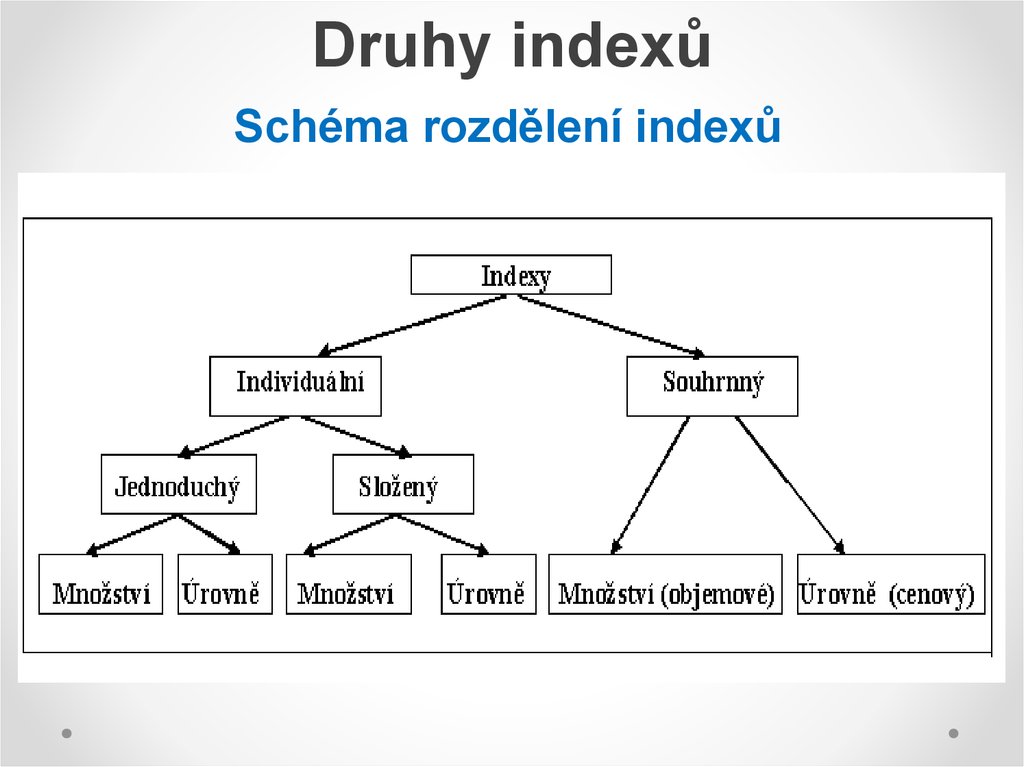
6. Druhy indexů

Schéma rozdělení indexů

7. Individuální indexy

Jednoduché individuální indexy
(srovnáváme dvě hodnoty téhož ukazatele)
(běžné období…1; základní období…0)
Jednoduchý index množství, týká se extenzitních
ukazatelů
q1
I
q0
q
Jednoduchý index úrovně, týká se intenzitních ukazatelů
p1
I
p0
p

8. Individuální indexy

Složené individuální indexy
Složený index množství
I
q
q
q
1
0
Složený index úrovně
pq
q
pq
q
1
p1
IPS
p0
1
1
0
0
0

9. Rozklad indexu proměnlivého složení

Vyjadřujeme jako součin dvou indexů
IPS = ISS . ISTR
Indexu stálého složení ISS
Index struktury ISTR

10. Rozklad indexu proměnlivého složení

p1q1
1. způsob rozkladu
p0 q1 p1q1
q1
q1
q1
p0 q0
p0 q0 p0 q1
q0
IPS
q0
ISTR0
q1
ISS1

11. Rozklad indexu proměnlivého složení

p1q1
2. způsob rozkladu
p1q0
p1q1
q0
q1
q1
p0 q0
p0 q0 p1q0
q0
IPS
q0
ISS0
q0
ISTR1

12.

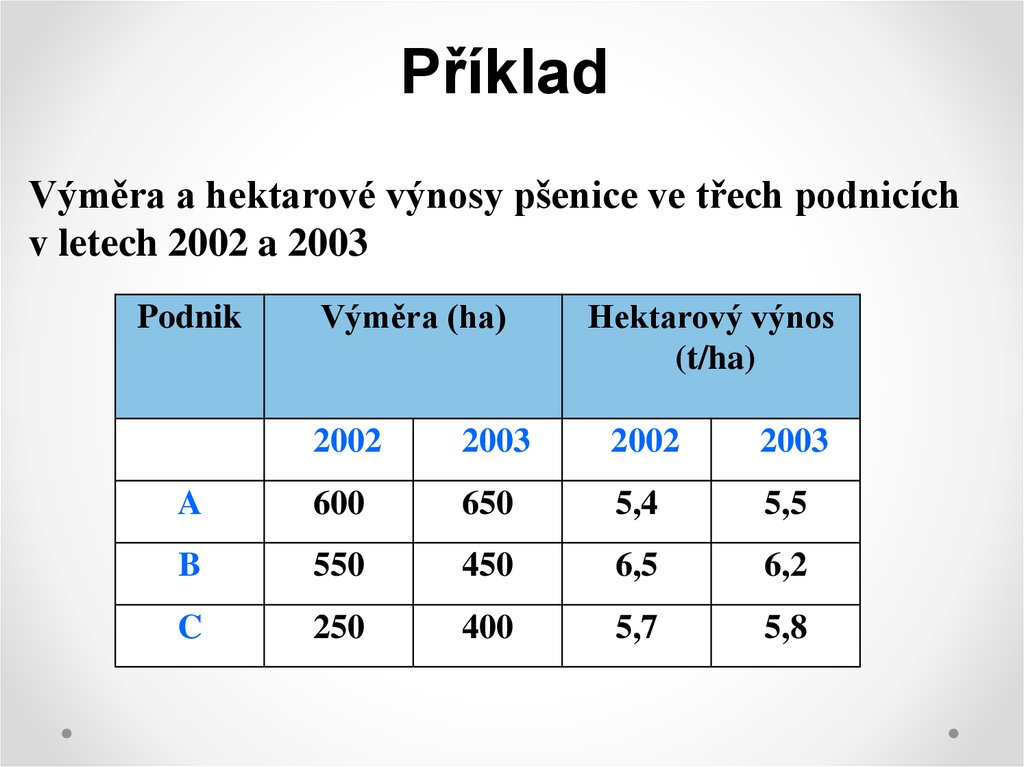
Příklad
Výměra a hektarové výnosy pšenice ve třech podnicích
v letech 2002 a 2003
Podnik
Výměra (ha)
Hektarový výnos
(t/ha)
2002
2003
2002
2003
A
600
650
5,4
5,5
B
550
450
6,5
6,2
C
250
400
5,7
5,8

13.

Změna výměry
A
B
C
Změna výnosu
q1 650
1,083
q 0 600
p1 5,5
1,019
p 0 5,4
nárůst o 8,3%
nárůst o 1,9%
q1 450
0,818
q 0 550
p1 6,2
0,954
p 0 6,5
pokles o 18,2%
pokles o 6,6%
q1 400
1,600
q 0 250
p1 5,8
1,018
p 0 5,7
nárůst o 60%
nárůst o 1,8%

14.

Změna průměrného hektarového výnosu v podnicích celkem
p1q1
q1
p 0q 0
q0
5,5.650 6,2.450 5,8.400
650 450 400
=
= 0,985
5,4.600 6,5.550 5,7 250
600 550 250
pokles hektar. výnosu o 1,5%
Jak se na změně výnosu podílela změna výměry v jednotlivých
podnicích
Index struktury
1) váhy z období základního
pokud by nedošlo ke změně výnosu
p 0q1
v podnicích, celkový průměrný výnos
q1
= 0,988 by vlivem změny výměry poklesl na 98,8%
p 0q 0
(uvažujeme-li výnosy z roku 2002)
q0

15.

2) váhy z období běžného
p1q1
q1
p1q 0
q0
= 0,993
pokud by nedošlo ke změně výnosu v podnicích,
celkový průměrný výnos by vlivem změny výměry poklesl
na 99,3% (uvažujeme-li výnosy z roku 2003)

16.

Jak se na změně hektar. výnosu podílela změna hektar.
výnosů v jednotlivých podnicích
Index stálého složení
1) váhy ze základního období
p1q 0
q0
= 0,991
p
q
0 0
q0
2) váhy z běžného období
p1q1
q1
= 0,996
p 0q1
q1
pokud by se nezměnila výměra pšenice v jednotlivých podnicích,
vlivem změny hektar. výnosů by průměrný hektarový výnos poklesl
na 99,1% (uvažujeme-li výměru z roku 2002),
resp. na 99,6% (uvažujeme-li výměru z roku 2003).

17. Souhrnné indexy

Indexy nestejnorodých extenzitních ukazatelů.
Souhrnné indexy úrovně - tzv. cenové indexy.
Souhrnné indexy množství - tzv. objemové indexy.

18. Souhrnné indexy úrovně

Laspeyresův index
(c)
0 1/ 0
q I
q c
q c
0 1
0
Paascheho index
(c)
1 1/ 0
qI
qc
q c
1 1
1 0
0

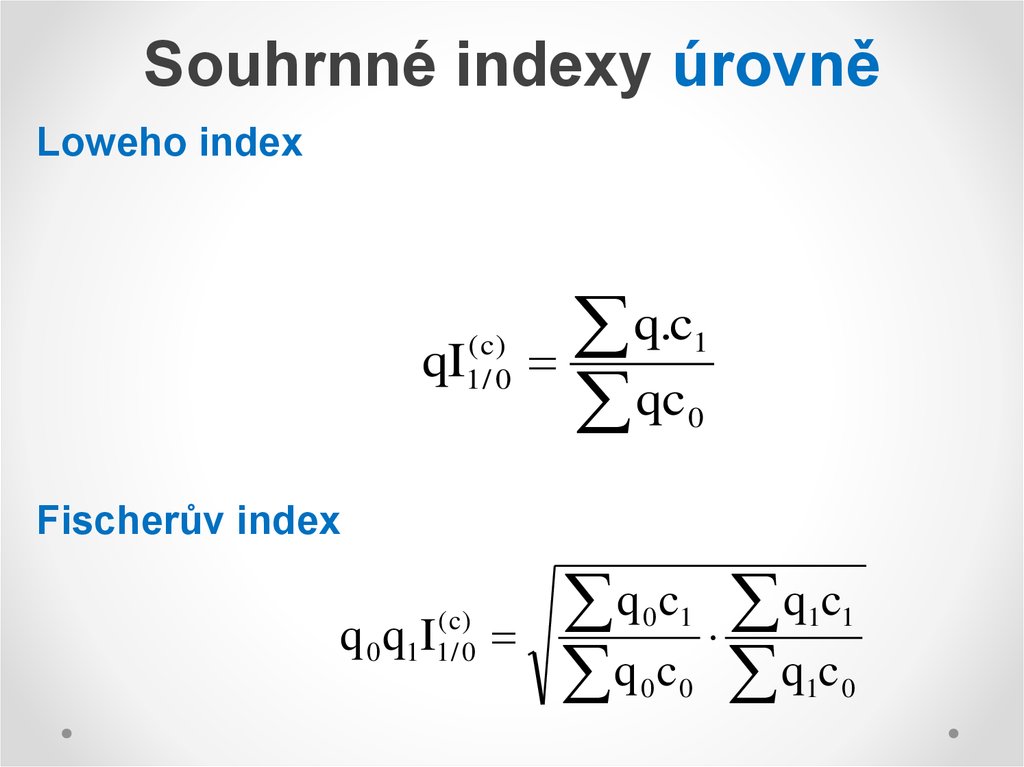
19. Souhrnné indexy úrovně

Loweho index
(c)
1/ 0
qI
q.c
qc
1
0
Fischerův index
(c)
0 1 1/ 0
q qI
q c q c
q c q c
0 1
1 1
0 0
1 0

20. Souhrnné indexy množství

Laspeyresův index
Paascheho index
(q)
0 1/ 0
cI
(q)
1 1/ 0
cI
q1c0
q 0 c0
q1c1
q0 c1

21. Souhrnné indexy množství

Loweho index
cI
(q)
1/ 0
Fischerův index
(q)
0 1 1/ 0
ccI
q1c
q0 c
q1c0 q1c1
q0 c0 q0 c1

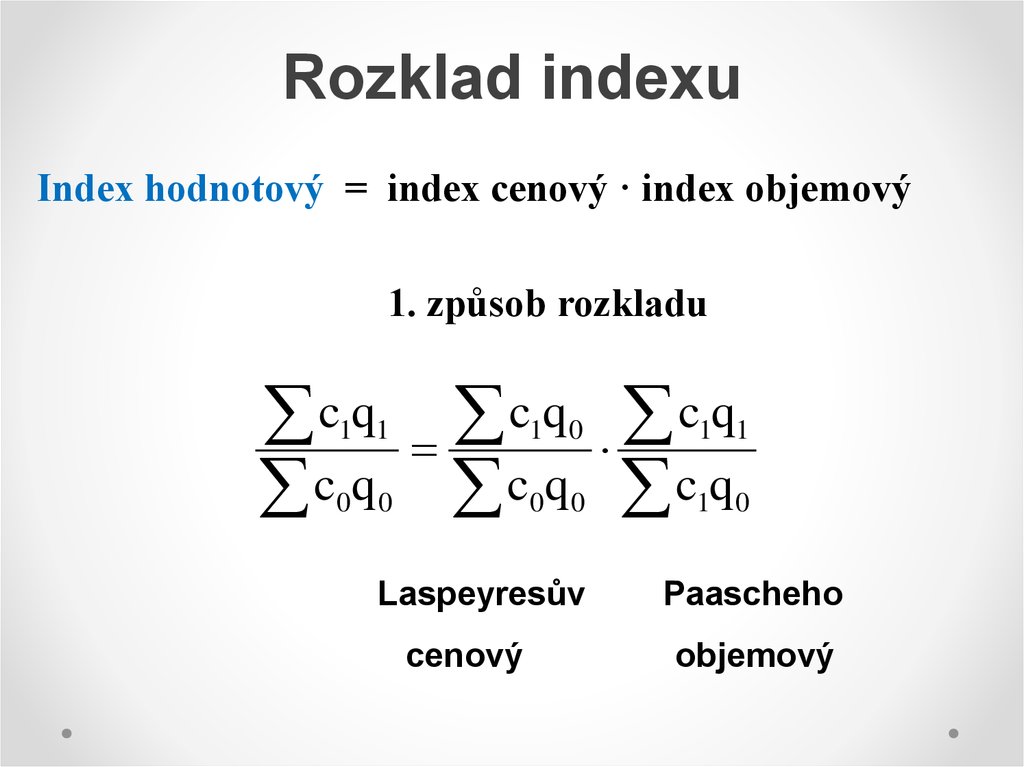
22. Rozklad indexu

Index hodnotový = index cenový · index objemový
1. způsob rozkladu
c q
c q
1 1
0 0
c q c q
c q c q
1 0
1 1
0 0
1 0
Laspeyresův
cenový
Paascheho
objemový

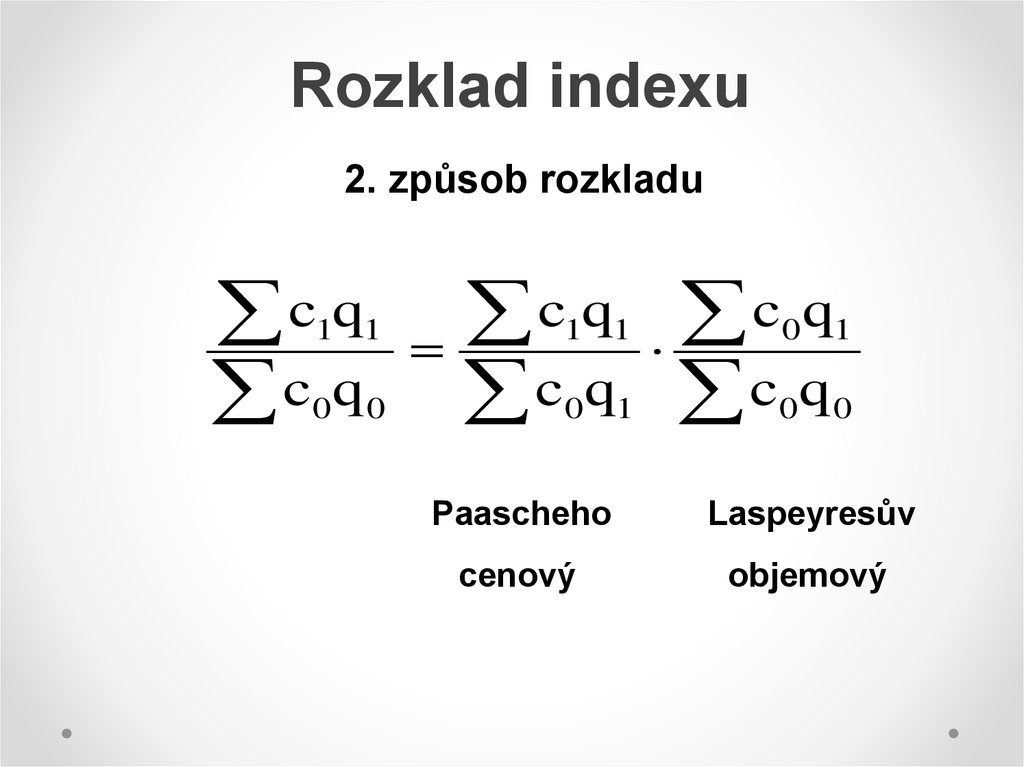
23. Rozklad indexu

2. způsob rozkladu
c q
c q
1 1
0
0
c q c q
c q c q
1 1
0
1
0
0
0
1
Paascheho
Laspeyresův
cenový
objemový

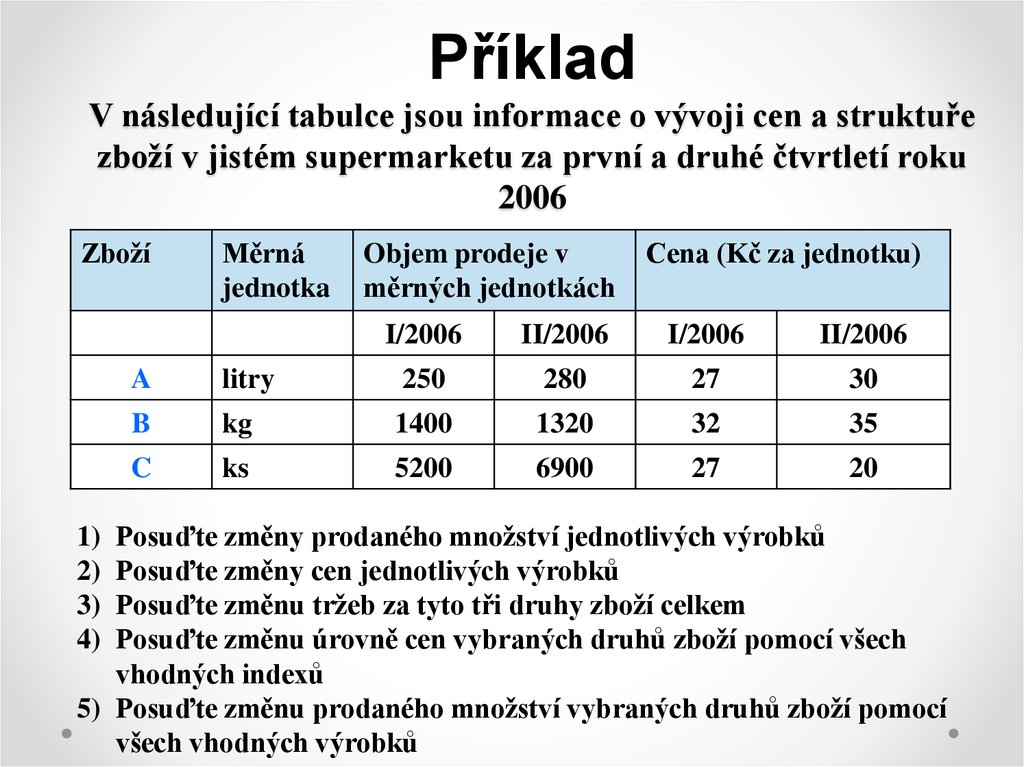
24. Příklad V následující tabulce jsou informace o vývoji cen a struktuře zboží v jistém supermarketu za první a druhé čtvrtletí

roku
2006
Zboží
Měrná
jednotka
Objem prodeje v
měrných jednotkách
Cena (Kč za jednotku)
I/2006
II/2006
I/2006
II/2006
A
litry
250
280
27
30
B
kg
1400
1320
32
35
C
ks
5200
6900
27
20
Posuďte změny prodaného množství jednotlivých výrobků
Posuďte změny cen jednotlivých výrobků
Posuďte změnu tržeb za tyto tři druhy zboží celkem
Posuďte změnu úrovně cen vybraných druhů zboží pomocí všech
vhodných indexů
5) Posuďte změnu prodaného množství vybraných druhů zboží pomocí
všech vhodných výrobků
1)
2)
3)
4)

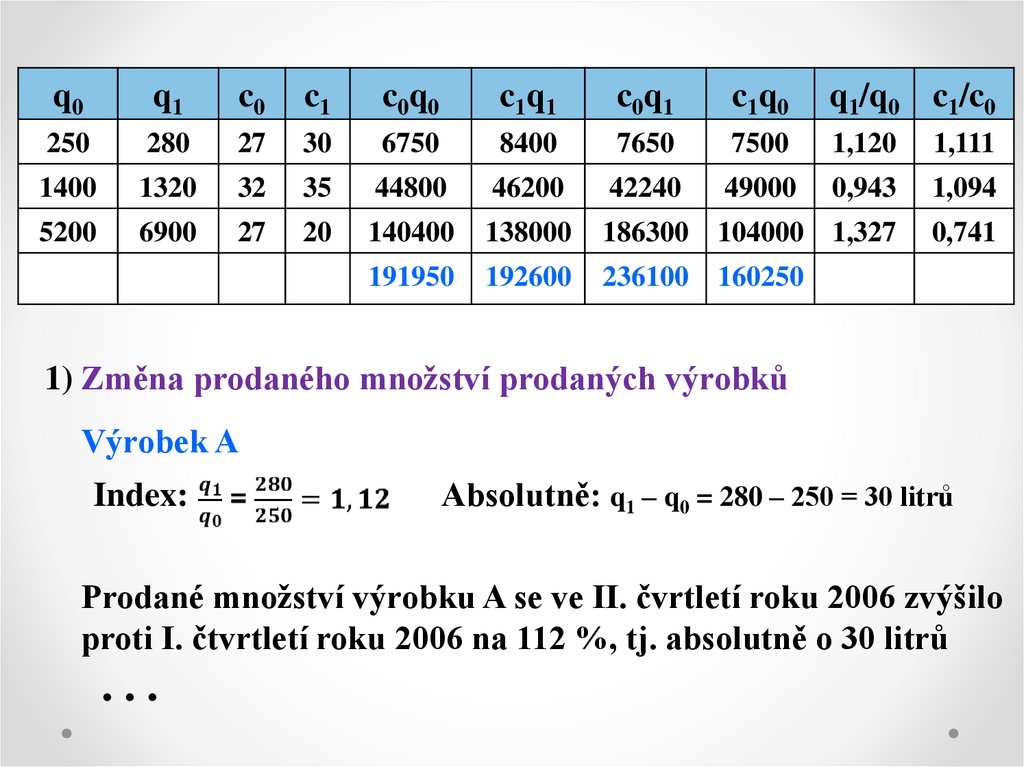
25.

q0
q1
c0
c1
c0q0
c1q1
c0q1
c1q0
q1/q0 c1/c0
250
280
27
30
6750
8400
7650
7500
1,120
1,111
1400
1320
32
35
44800
46200
42240
49000
0,943
1,094
5200
6900
27
20
140400
138000
186300 104000 1,327
0,741
191950
192600
236100 160250
1) Změna prodaného množství prodaných výrobků
Výrobek A
Index:
Absolutně: q1 – q0 = 280 – 250 = 30 litrů
Prodané množství výrobku A se ve II. čvrtletí roku 2006 zvýšilo
proti I. čtvrtletí roku 2006 na 112 %, tj. absolutně o 30 litrů
...

26. 2) Změna ceny jednotlivých výrobků

Výrobek A
Absolutně: c1 – c0 = 30 – 27 = 3 Kč
Cena výrobku A vyrostla ve sledovaném období na 111,1 %,
tj. o 3 Kč na litr.
...
Prohlédni skripta Statistika II, str. 74 - 76

27.  

Absolutně: Δ = - 31 450 Kč
Paascheho cenový index:
Absolutně: Δ = - 43 500 Kč
Pokud by došlo pouze ke změně cen, vedlo by to ke snížení tržeb
na 83,6 %, pokud by bylo uvažováno množství z období
základního, resp. Na 81,6 %, pokud by bylo uvažováno množství
z obdoví běžného.

28. 5) Změna prodaného množství vybraných druhů zboží pomocí objemových indexů

Laspeyersův objemový index:
Absolutně: Δ = + 44 150
Paascheho objemový index:
Absolutně: Δ = + 32 100
Pokud by ve sledovaném období došlo pouze ke změně
prodaného množství, vedlo by to ke zvýšení tržeb o 20%, pokud
by bylo uvažováno množství z období základního, resp. O 23 %,
pokud by bylo uvažováno množství z období běžného.