Построение теней

1. Лекция № 17 Построение теней.

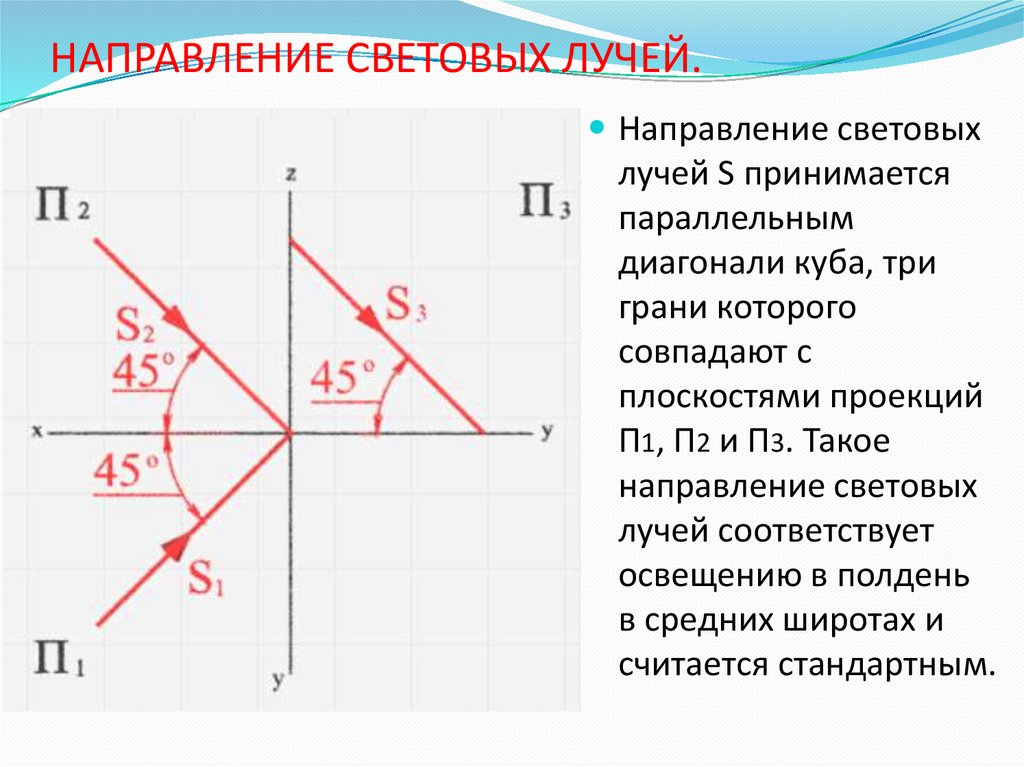
Ст.преподаватель Войцехович И.В.

2. НАПРАВЛЕНИЕ СВЕТОВЫХ ЛУЧЕЙ.

Направление световых
лучей S принимается
параллельным
диагонали куба, три
грани которого
совпадают с
плоскостями проекций
П1, П2 и П3. Такое
направление световых
лучей соответствует
освещению в полдень
в средних широтах и
считается стандартным.

3.

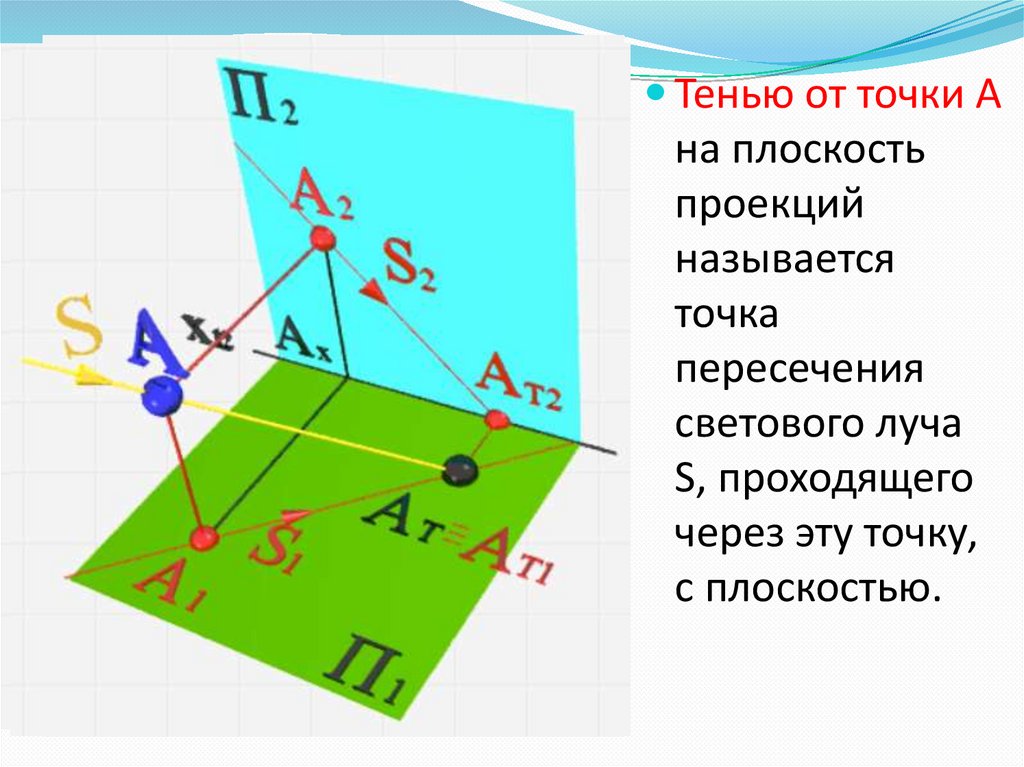
Тенью от точки А
на плоскость
проекций
называется
точка
пересечения
светового луча
S, проходящего
через эту точку,
с плоскостью.

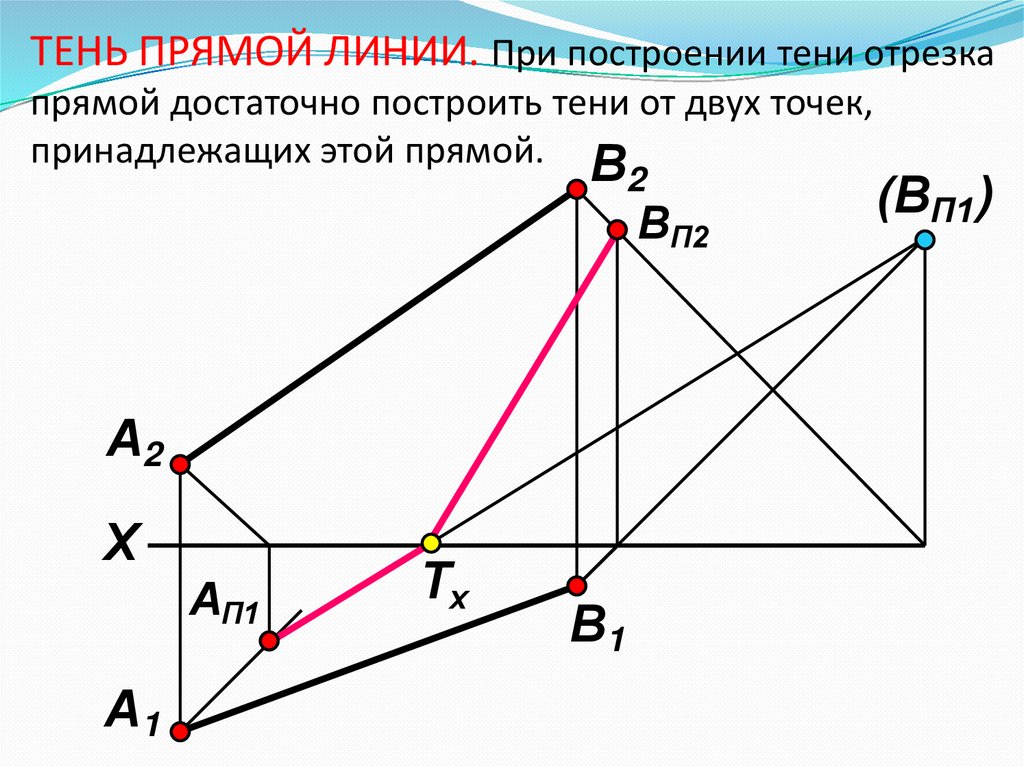
4. ТЕНЬ ПРЯМОЙ ЛИНИИ. При построении тени отрезка прямой достаточно построить тени от двух точек, принадлежащих этой прямой.

В
2
ВП2
А2
Х
АП1
А1
Тх
В1
(ВП1)

5. Если тень отрезка прямой падает одновременно на обе плоскости проекций, необходимо найти точку преломления тени на оси Х.

Если след светового луча находится в первой
четверти пространства, тень называется
реальной или действительной.
Если след светового луча падает в другую
четверть пространства, тень называется
мнимой, а ее обозначение берется в круглые
скобки.

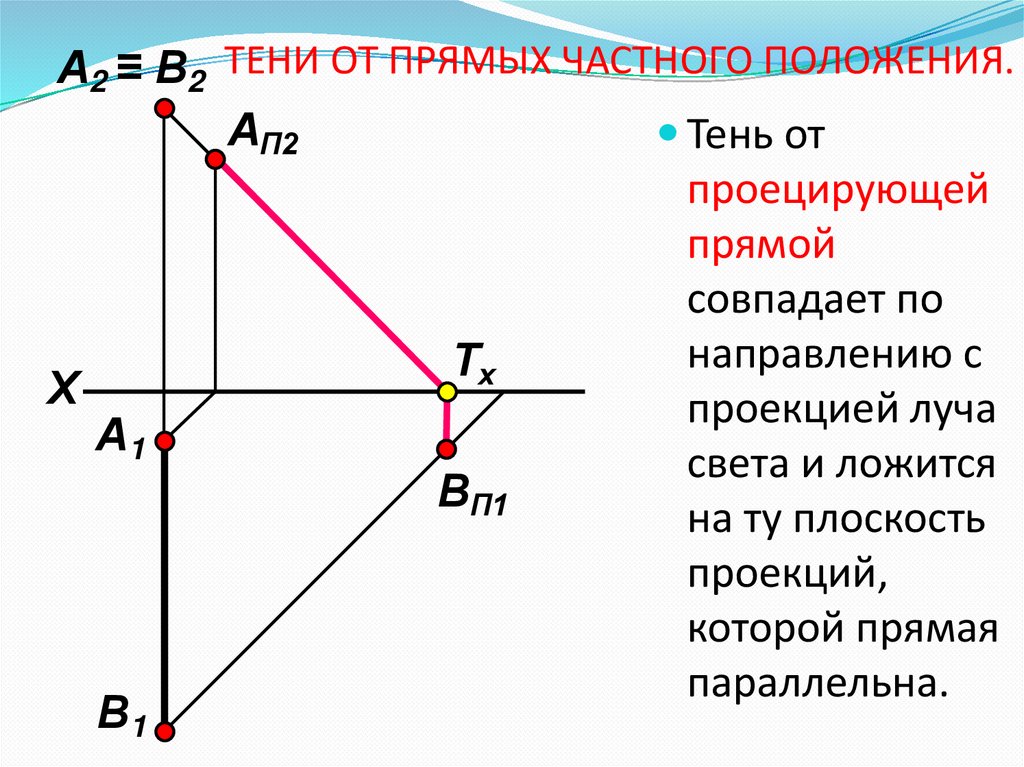
6. ТЕНИ ОТ ПРЯМЫХ ЧАСТНОГО ПОЛОЖЕНИЯ.

А2 ≡ В2 ТЕНИ ОТ ПРЯМЫХ ЧАСТНОГО ПОЛОЖЕНИЯ.
АП2
Тень от
проецирующей
прямой
совпадает по
направлению с
Тх
Х
проекцией луча
А1
света и ложится
ВП1
на ту плоскость
проекций,
которой прямая
параллельна.
В1

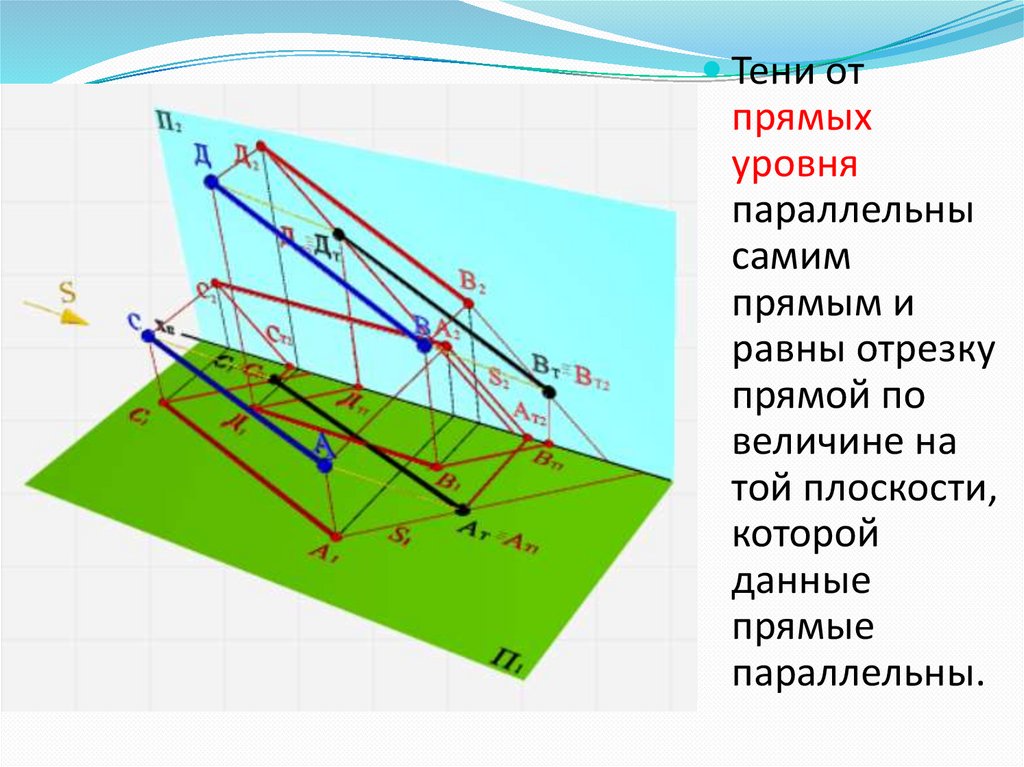
7.

Тени от
прямых
уровня
параллельны
самим
прямым и
равны отрезку
прямой по
величине на
той плоскости,
которой
данные
прямые
параллельны.

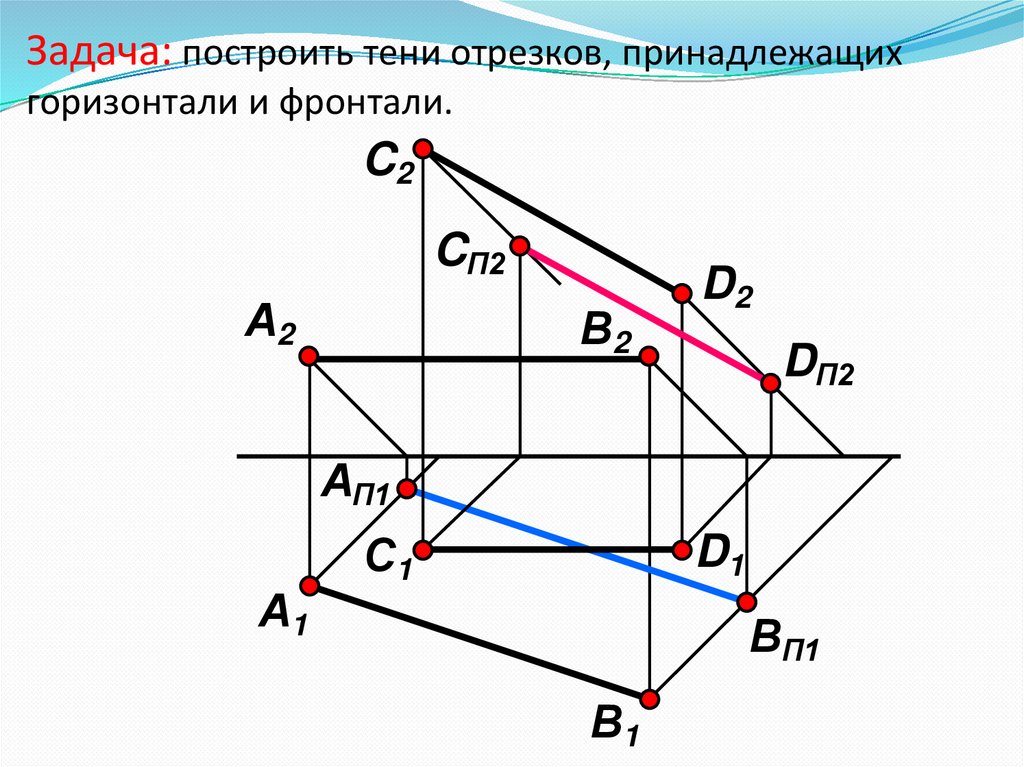
8. Задача: построить тени отрезков, принадлежащих горизонтали и фронтали.

C2
CП2
А2
В2
D2
DП2
АП1
А1
С1
D1
ВП1
В1

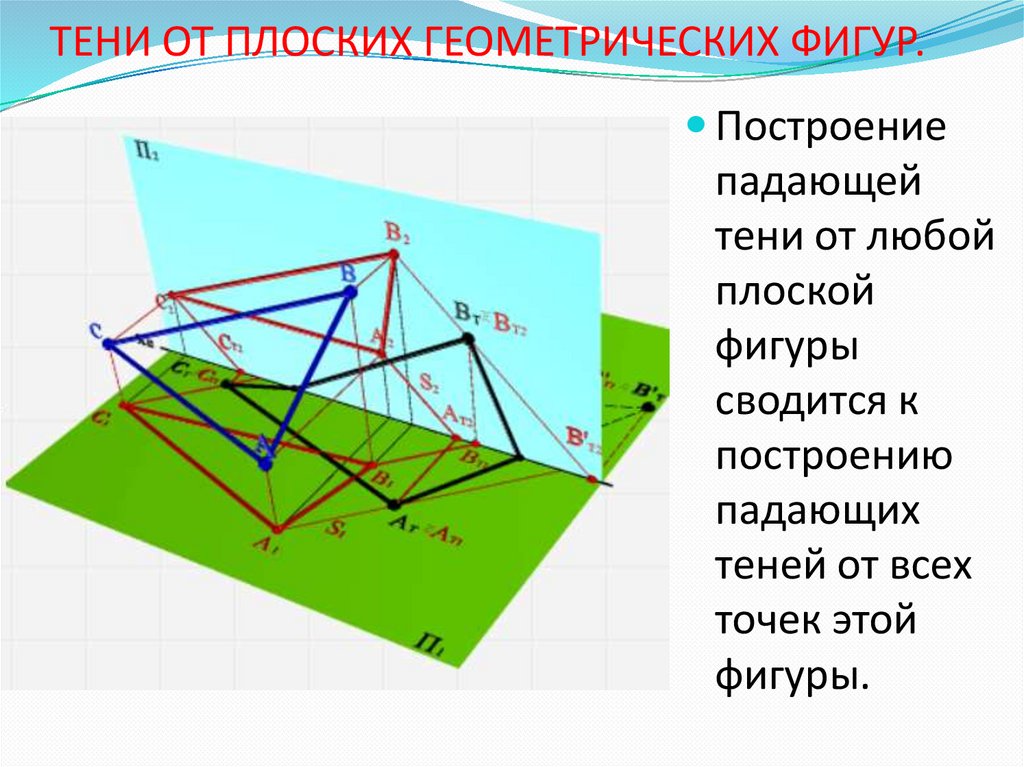
9. ТЕНИ ОТ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР.

Построение
падающей
тени от любой
плоской
фигуры
сводится к
построению
падающих
теней от всех
точек этой
фигуры.

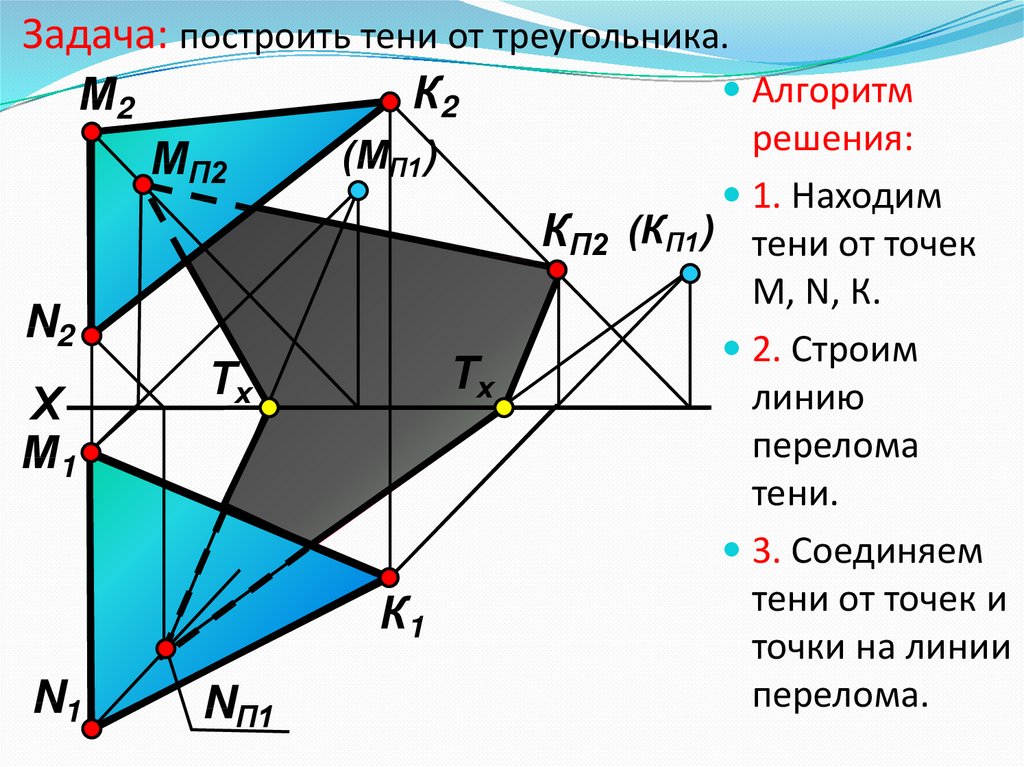
10. Задача: построить тени от треугольника.

Алгоритм
К2
М2
решения:
(М
)
МП2
П1
1. Находим
КП2 (КП1) тени от точек
М, N, К.
N2
Х
М1
Тх
Тх
К1
N1
NП1
2. Строим
линию
перелома
тени.
3. Соединяем
тени от точек и
точки на линии
перелома.

11.

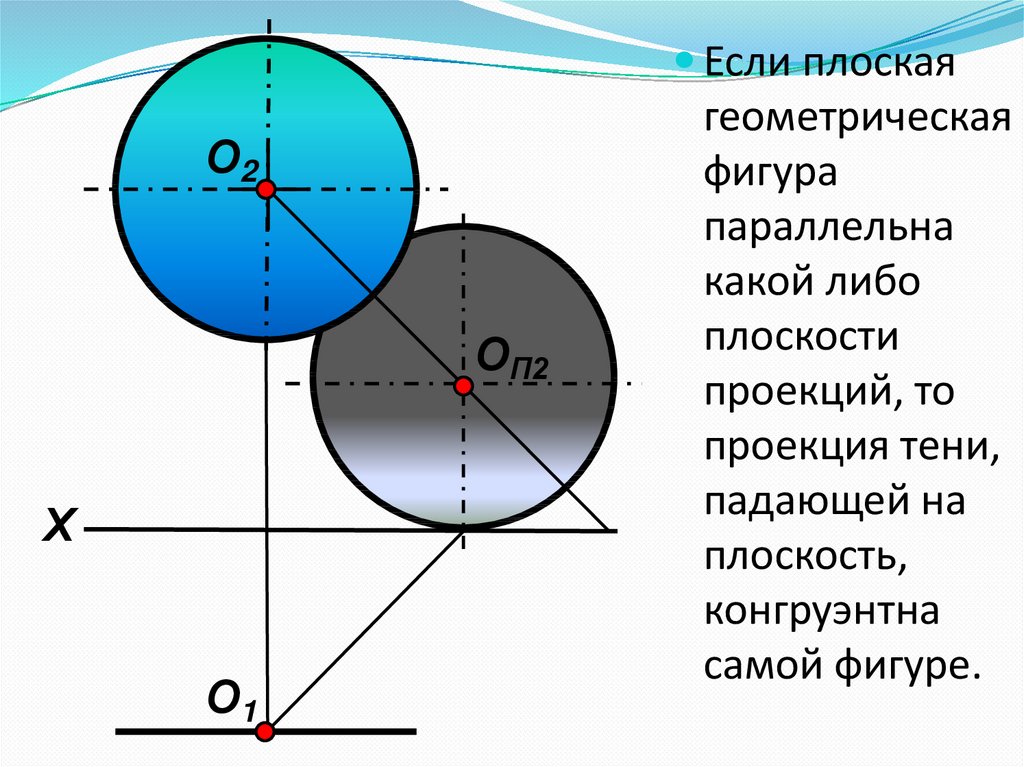
Если плоская
О2
ОП2
Х
О1
геометрическая
фигура
параллельна
какой либо
плоскости
проекций, то
проекция тени,
падающей на
плоскость,
конгруэнтна
самой фигуре.

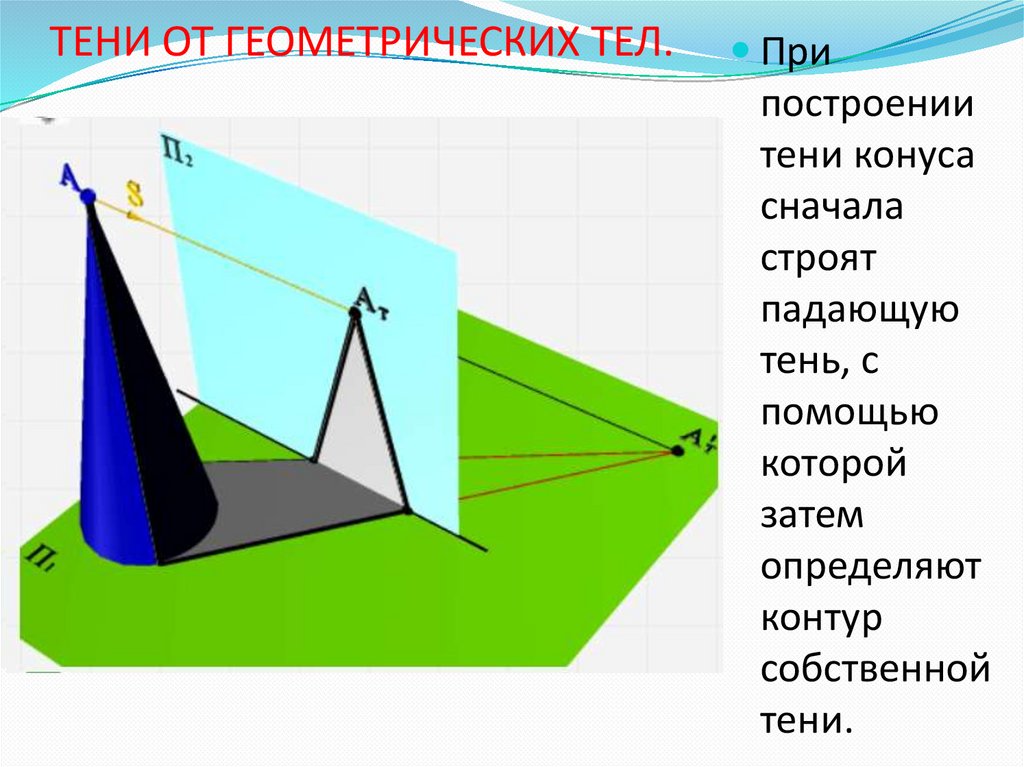
12. ТЕНИ ОТ ГЕОМЕТРИЧЕСКИХ ТЕЛ.

При
построении
тени конуса
сначала
строят
падающую
тень, с
помощью
которой
затем
определяют
контур
собственной
тени.

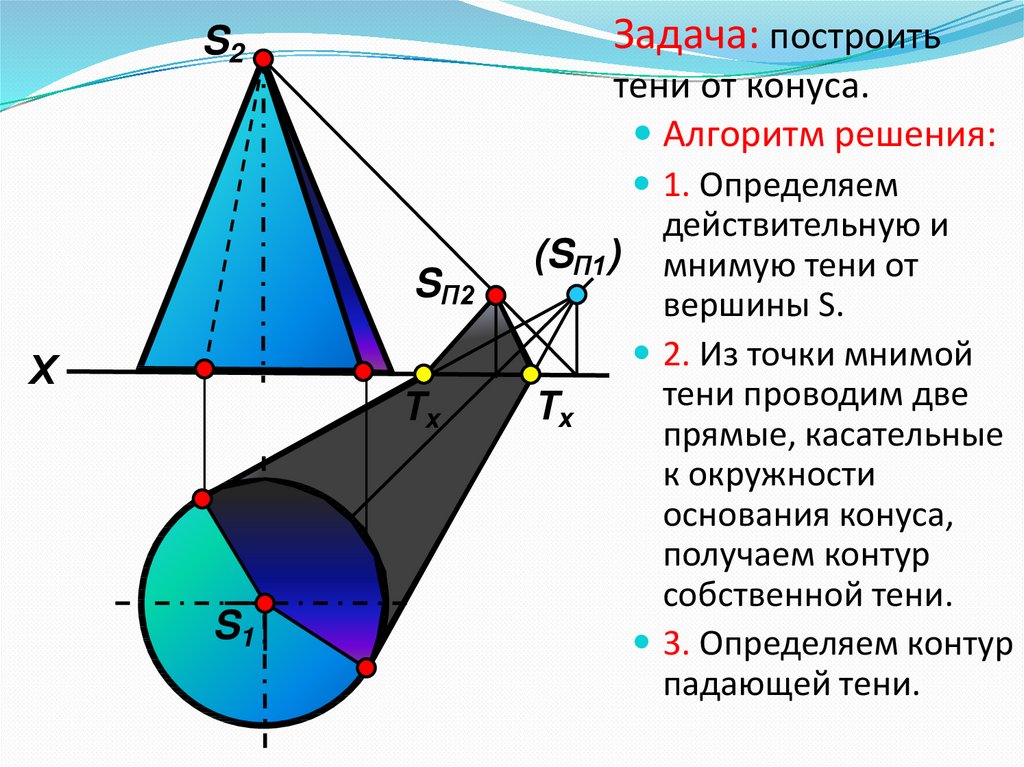
13. Задача: построить тени от конуса.

Задача: построить
S2
тени от конуса.
Алгоритм решения:
1. Определяем
SП2
Х
Тх
S1
действительную и
(SП1) мнимую тени от
вершины S.
2. Из точки мнимой
тени проводим две
Тх
прямые, касательные
к окружности
основания конуса,
получаем контур
собственной тени.
3. Определяем контур
падающей тени.

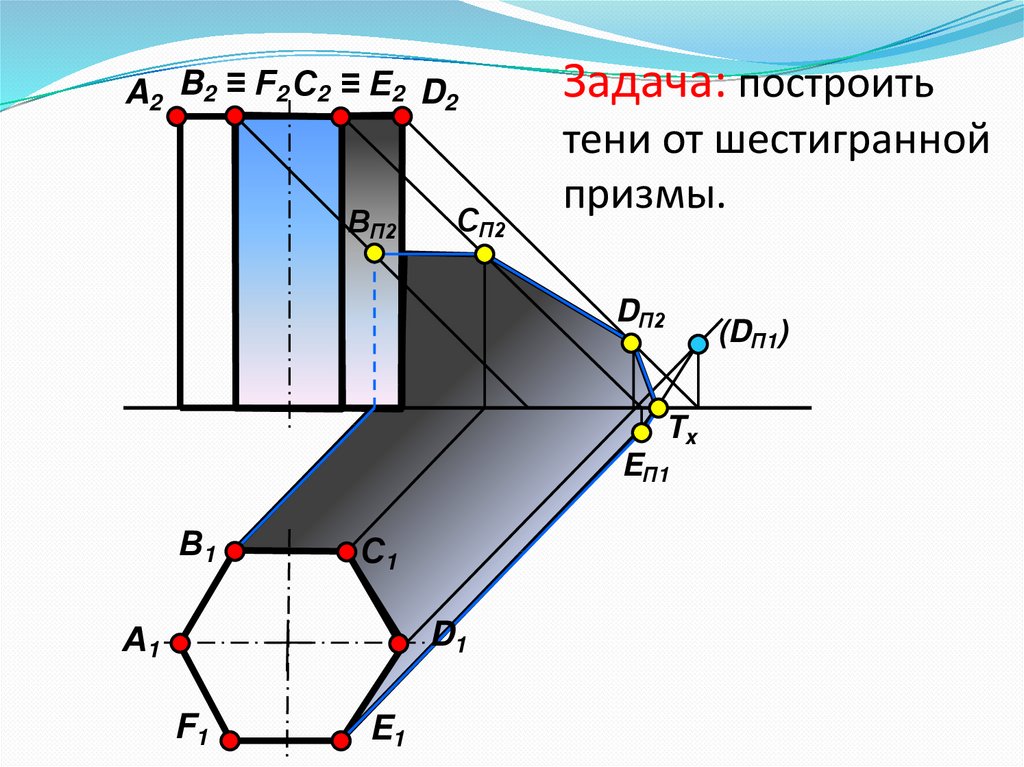
14. Задача: построить тени от шестигранной призмы.

A2 B2 ≡ F2 С2 ≡ Е2 D2
ВП2
СП2
Задача: построить
тени от шестигранной
призмы.
DП2
(DП1)
Tx
EП1
В1
С1
А1
D1
F1
E1

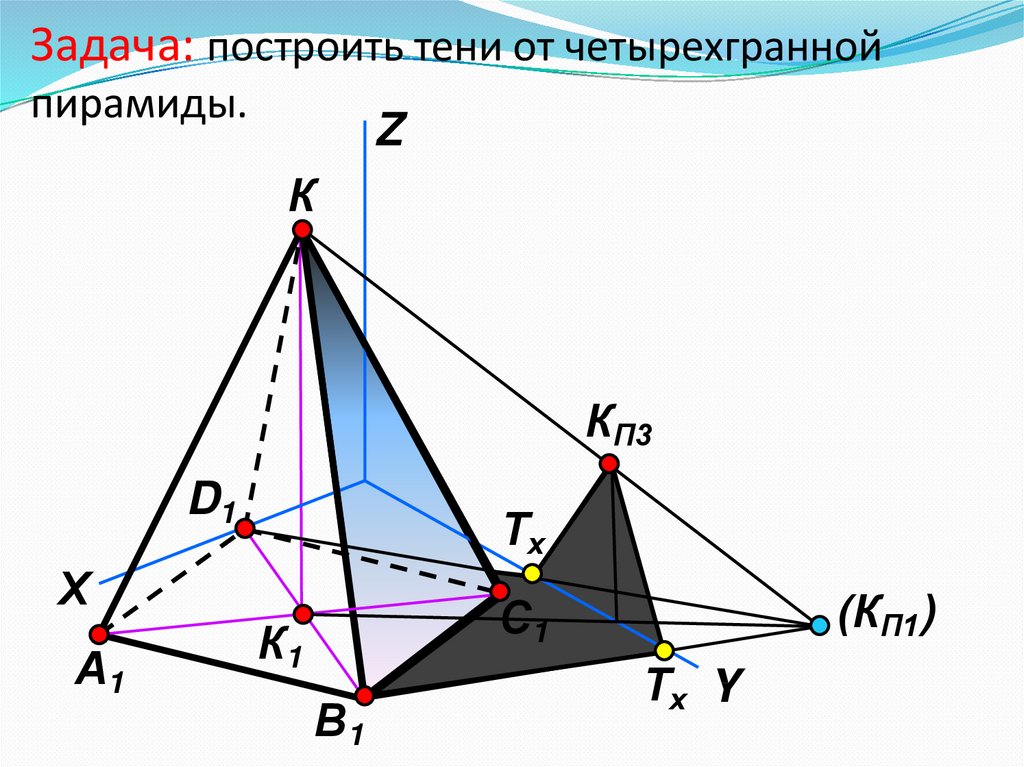
15. Задача: построить тени от четырехгранной пирамиды.

Z
К
КП3
D1
Тх
Х
А1
(КП1)
С1
К1
В1
Тх Y