Похожие презентации:
Численные методы
1.
Численные методы2.
│x – xпр │< εВеличину ε также называют допустимой ошибкой,
которую можно задать по своему усмотрению.
Задача решения нелинейного уравнения состоит из
двух этапов:
• локализация корней, т.е. определение интервала
изоляции (интервала неопределенности), в котором
расположен корень;
• определение с заданной точностью точности ε
приближенного значения корня.
3. Отделение корней
Отделение корней можно проводить графически ианалитически.
Для того чтобы графически отделить корни
уравнения, необходимо построить график функции
f(x). Абсциссы точек его пересечения с осью Ox
являются действительными корнями уравнения.
4.
Аналитическое отделение корней основано наследующих теоремах.
Теорема 1. Если непрерывная функция f(x)
принимает на концах отрезка [a; b] значения разных
знаков, т.е.
то на этом отрезке содержится, по крайней мере, один
корень уравнения.
Теорема 2. Если непрерывная на отрезке [a; b]
функция f(x) принимает на концах отрезка значения
разных знаков, а производная f'(x) сохраняет знак
внутри указанного отрезка, то внутри отрезка
существует единственный корень уравнения f(x) = 0.
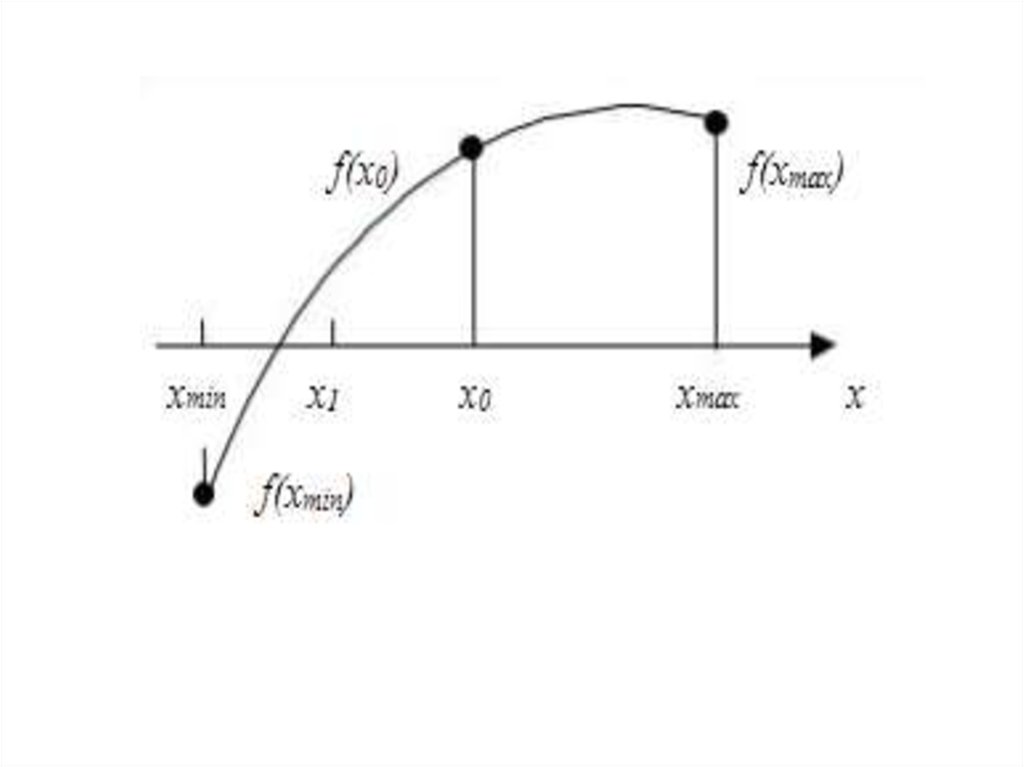
5. Метод половинного деления (метод дихотомии)
Выбор начального приближения состоит в том, чтобызадать границы xmin и xmax конечного интервала
значений x, в котором находится корень уравнения
(только один корень уравнения для случая нескольких
корней). Поскольку действительное положение корня
уравнения внутри интервала неизвестно, примем в
качестве начального приближения точку,
соответствующую середине интервала
x0=0,5(xmin + xmax).
6.
7.
Условие остановки итерационного процессаможет быть сформулировано несколькими
способами:
• n = nmax, где nmax - заранее установленное
максимальное число шагов итерационного
процесса. Это условие может применяться
при ограниченных ресурсах времени на
решение;
• (xmax – xmin) < ε , где ε - требуемая точность
вычисления корня уравнения определяется,
исходя из условий дальнейшего
практического использования полученного
решения.
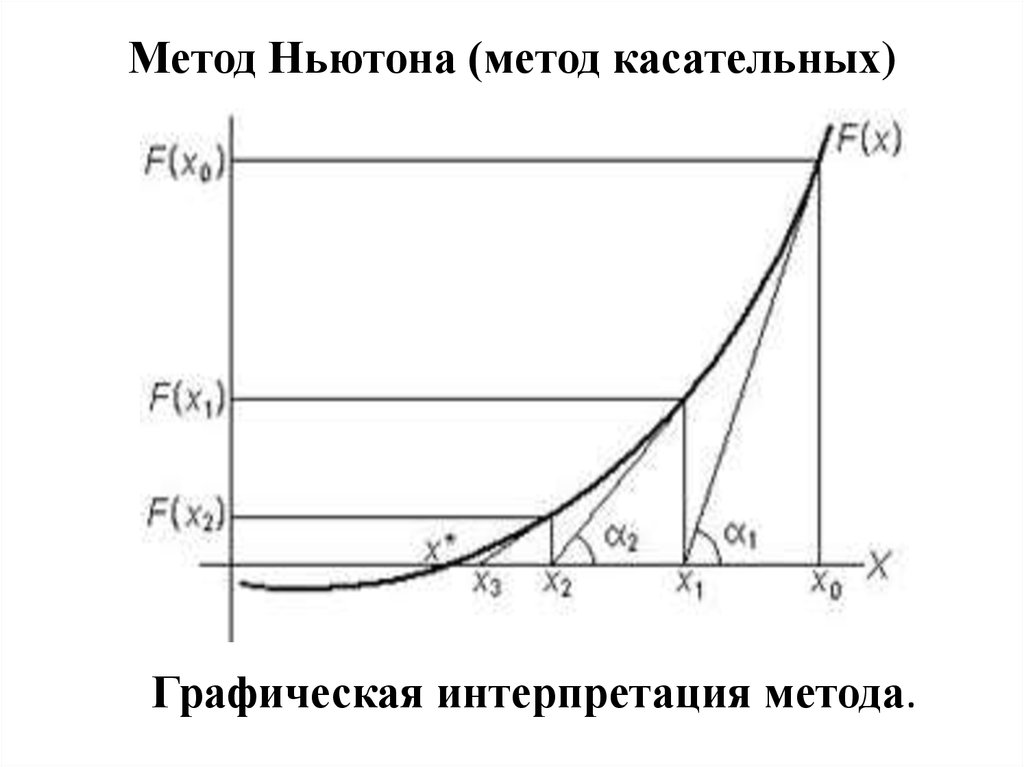
8. Метод Ньютона (метод касательных)
Графическая интерпретация метода.9.
В общем случае вычислительный процесс методаНьютона выражается формулой:
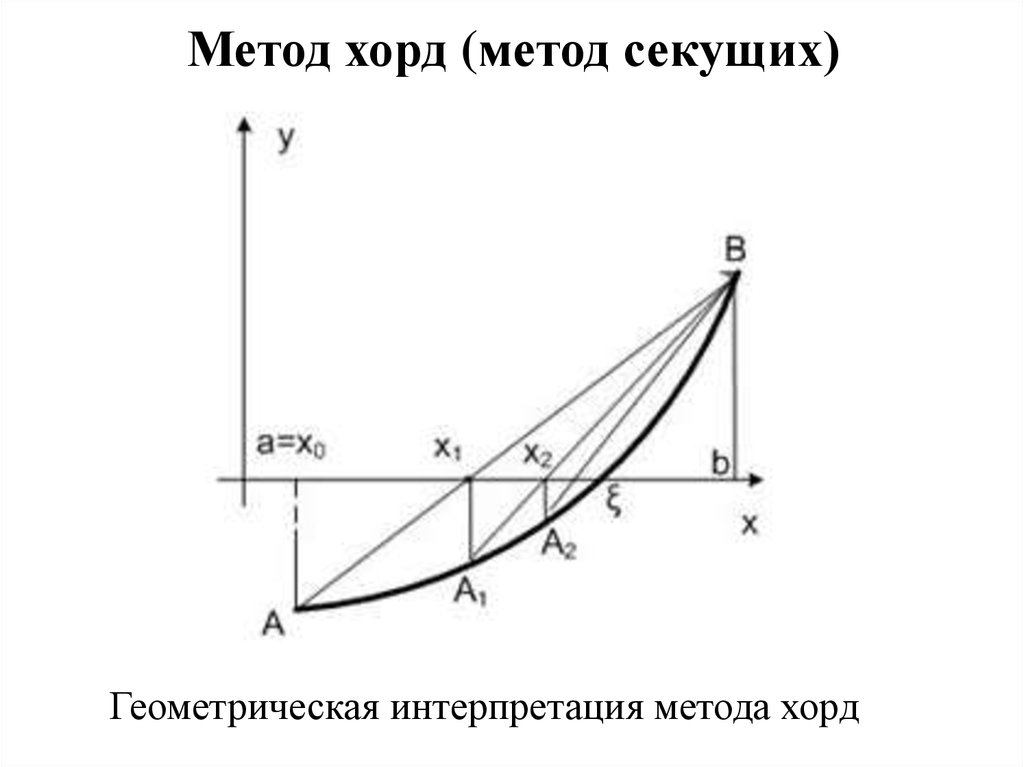
10. Метод хорд (метод секущих)
Геометрическая интерпретация метода хорд11.
Положим y = 0 и найдем значение х = х1 (очередноеприближение):
Повторим процесс вычислений для получения
очередного приближения к корню - х2:
12.
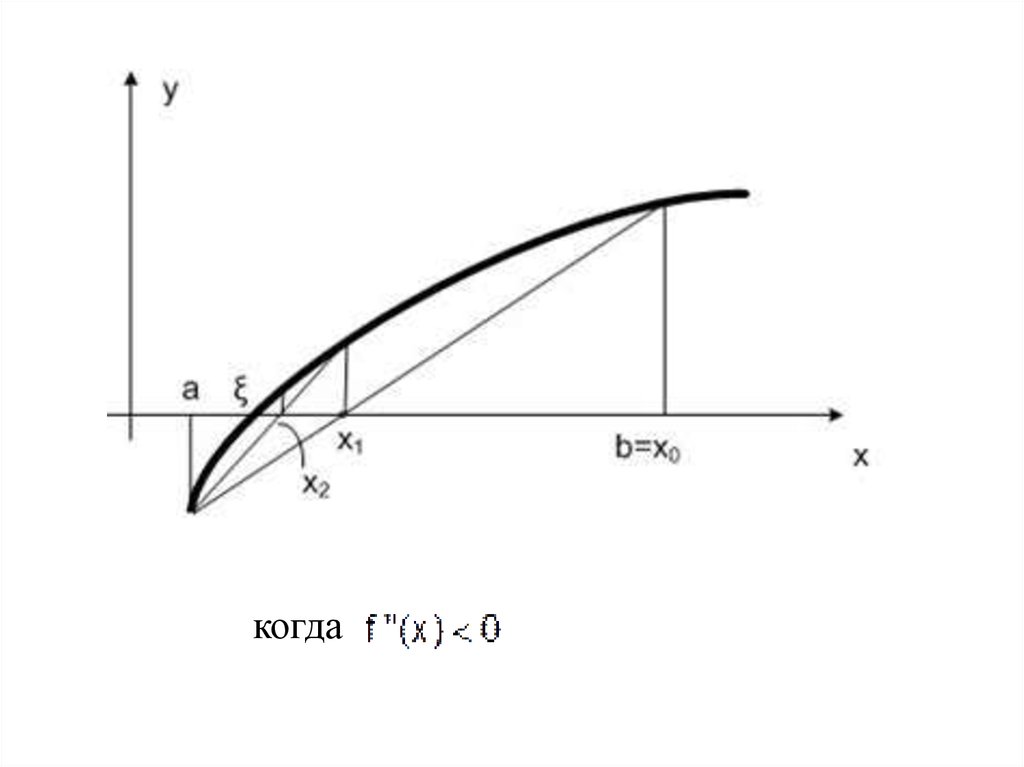
В случаебудет иметь вид
расчетная формула метода хорд
Эта формула справедлива, когда за неподвижную
точку принимается точка b, а в качестве начального
приближения выступает точка a.
13.
когда14.
Уравнение прямой для этого случая имеет видОчередное приближение х1 при y = 0
Тогда формула метода хорд для этого случая имеет вид
15. Метод простых итераций
Для реализации этого метода исходное уравнениеf(x)=0 предварительно преобразуется к виду x=ϕ(x).
Обычно это можно осуществить несколькими
способами. Выбрав начальное приближение x0
(реализуют следующий итерационный процесс:
x1=ϕ(x0) ,x2=ϕ(x1), и т.д.
16.
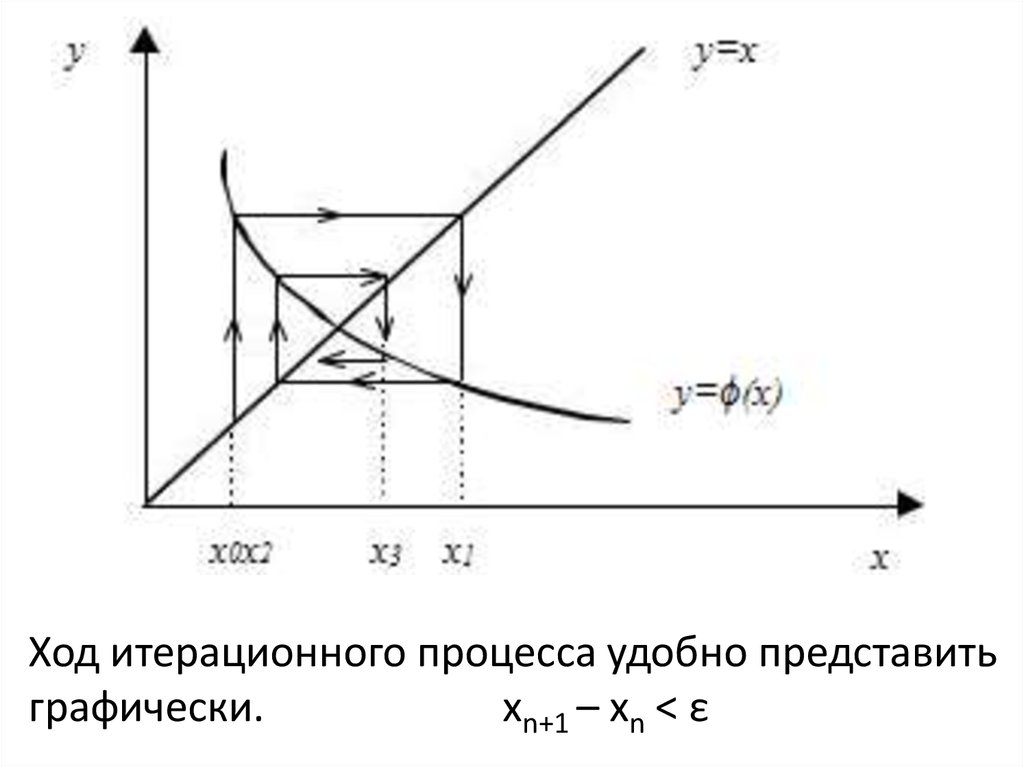
Ход итерационного процесса удобно представитьграфически.
xn+1 – xn < ε
17. Задача численного интегрирования
В ряде задач возникает необходимость вычисленияопределенного интеграла от некоторой функции:
где f(x) – подынтегральная функция, непрерывная на
отрезке [a, b].
Геометрический смысл интеграла заключается в том, что
если f(x)>0 на отрезке [a, b], то интеграл
численно равен площади фигуры, ограниченной
графиком функции y=f(x), отрезком оси абсцисс,
прямой x=a и прямой x=b.
18.
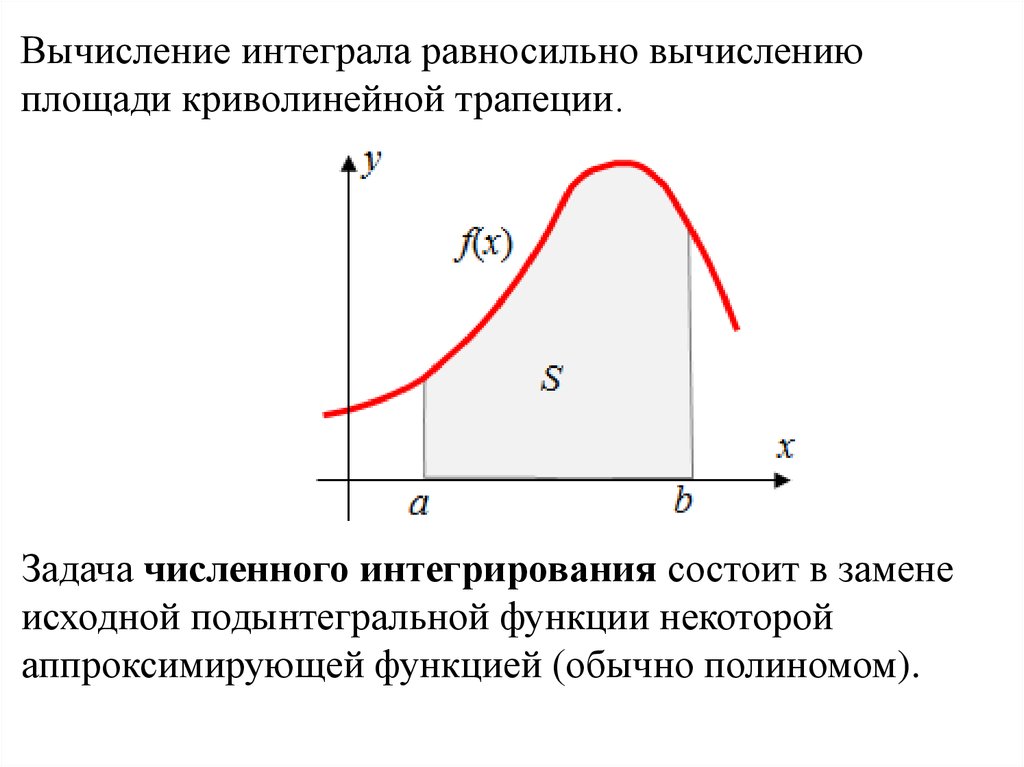
Вычисление интеграла равносильно вычислениюплощади криволинейной трапеции.
Задача численного интегрирования состоит в замене
исходной подынтегральной функции некоторой
аппроксимирующей функцией (обычно полиномом).
19.
Численное интегрирование применяется, когда:• сама подынтегральная функция не задана
аналитически, а например, представлена в виде
таблицы значений;
• аналитическое представление подынтегральной
функции известно, но её первообразная не выражается
через аналитические функции.
Способы численного вычисления определенных
интегралов основаны на замене интеграла конечной
суммой:
где Сj– числовые коэффициенты, выбор которых
зависит от выбранного метода численного
интегрирования,
20.
хj– узлы интегрированияВыражение называют квадратурной формулой.
Разделим отрезок [a, b] на N равных частей, то есть
на N элементарных отрезков. Длина каждого
элементарного отрезка:
Тогда значение интеграла можно представить в виде:
Из этого выражения видно, что для численного
интегрирования на отрезке [a, b] достаточно построить
квадратурную формулу на каждом частичном отрезке
21.
Погрешность квадратурной формулыопределяется выражением:
и зависит от выбора коэффициентов Сj и от
расположения узлов хj
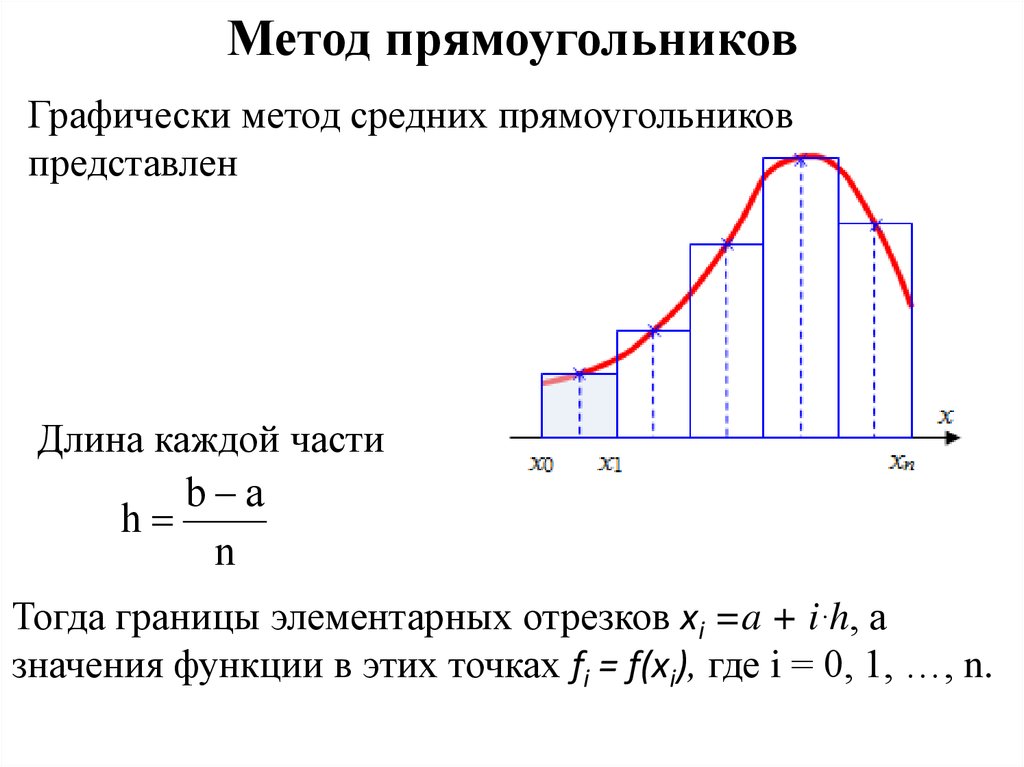
22. Метод прямоугольников
Графически метод средних прямоугольниковпредставлен
Длина каждой части
b a
h
n
Тогда границы элементарных отрезков xi =a + i·h, а
значения функции в этих точках fi = f(xi), где i = 0, 1, …, n.
23.
bn 1
f ( x)dx h f ( x
a
i 0
i 1 / 2
)
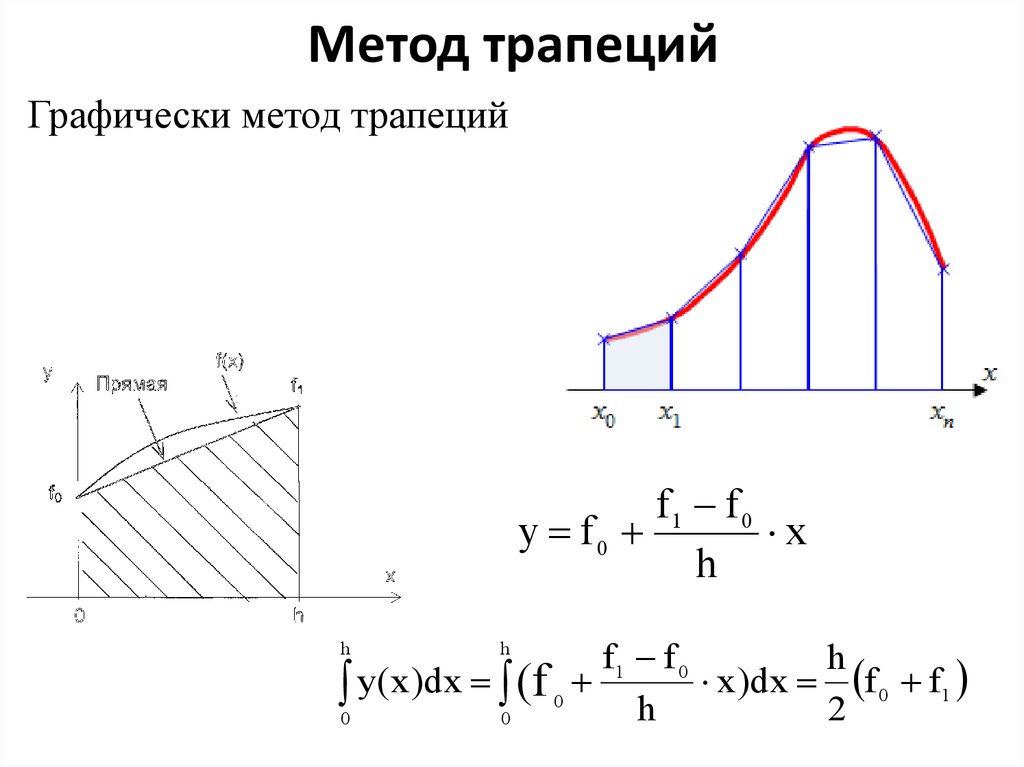
24. Метод трапеций
Графически метод трапецийf1 f 0
y f0
x
h
f1 f 0
h
0 y( x )dx 0 (f 0 h x )dx 2 f 0 f1
h
h
25.
формула трапеций имеет вид f ( x )dx h * (f 0 f1 )2
0
b a
h
Тогда границы элементарных отрезков xi =a +
n
i*h, а значения функции в этих точках fi = f(xi),
где i= 0, 1, …, n.
h
xi 1
Для отрезка [xi, xi+1] длины h
f ( x)dx h ( f
i
f i 1 )
xi
Суммируя левую и правую части этого соотношения от
i=0 до i=n-1
f0
f 0 f n n 1
fn
fi )
a f ( x )dx h ( 2 f1 f 2 f 3 ... f n 1 2 ) h ( 2
i 1
b
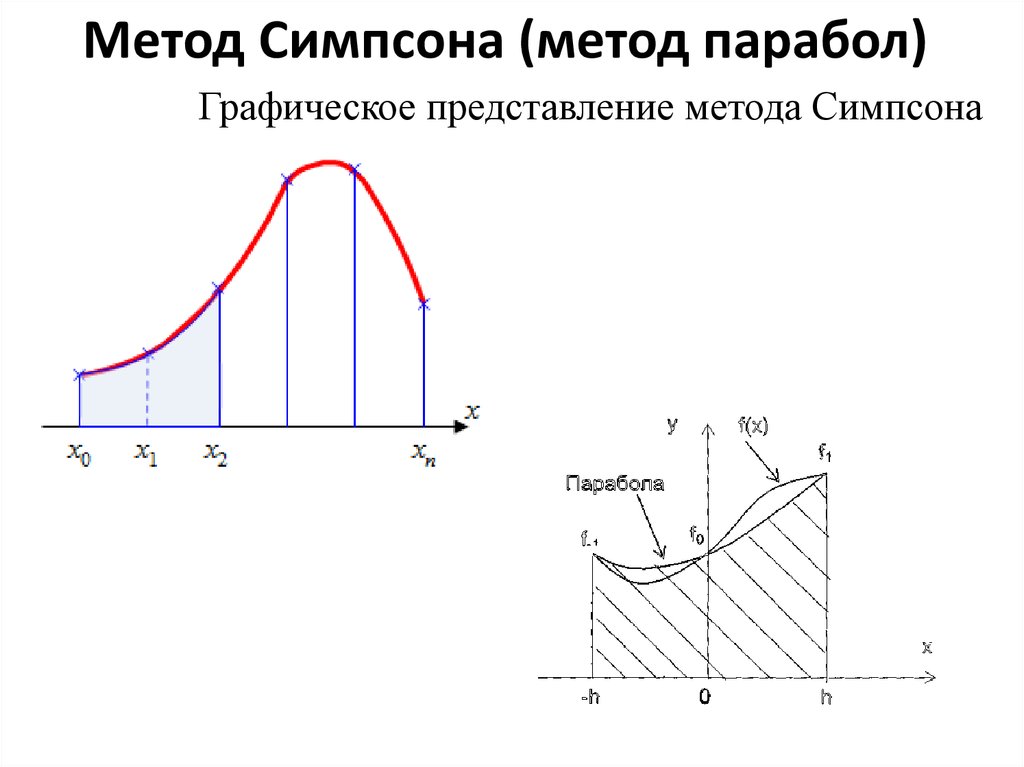
26. Метод Симпсона (метод парабол)
Графическое представление метода Симпсона27.
Указанная парабола задается уравнениемf 1 2 f 0 f1 2
f1 f 1
y f0
x
x
2
2h
2h
h
h
h y( x)dx 3 ( f 1 4 f 0 f1 )
b a
h
2 n
h
h
h f ( x)dx 3 ( f 1 4 f 0 f1 )
Тогда границы элементарных отрезков xi a i h
а значения функции в этих точках fi f ( xi ) , где i 0,1,..,2 n
Перепишем каноническую квадратурную формулу
Симпсона применительно к отрезку x2i , x2i 2
длины 2·h
28.
x2 i 2x2 i
h
f ( x)dx ( f 2i 4 f 2i 1 f 2i 21 )
3
Суммируя левую и правую части этого соотношения от
i 0 до i n 1, получаем усложненную квадратурную
формулу Симпсона
b
a
N
N 1
h
h
f ( x)dx ( f 0 4 f1 2 f 2 4 f 3 ... 4 f 2 N 1 f 2 N ) ( f 0 f 2 N 4 f 2i 1 2 f 2i )
3
3
i 1
i 1
29.
30.
1. Общие сведения. Классыэлектромеханических приборов,
измеряющих напряжение и силу тока.
Цифровые вольтметры.
2. Универсальные осциллографы. Техника
осциллографирования непрерывных и
импульсных сигналов.
3. Цифровые и аналоговые методы
измерения частоты и интервалов времени.















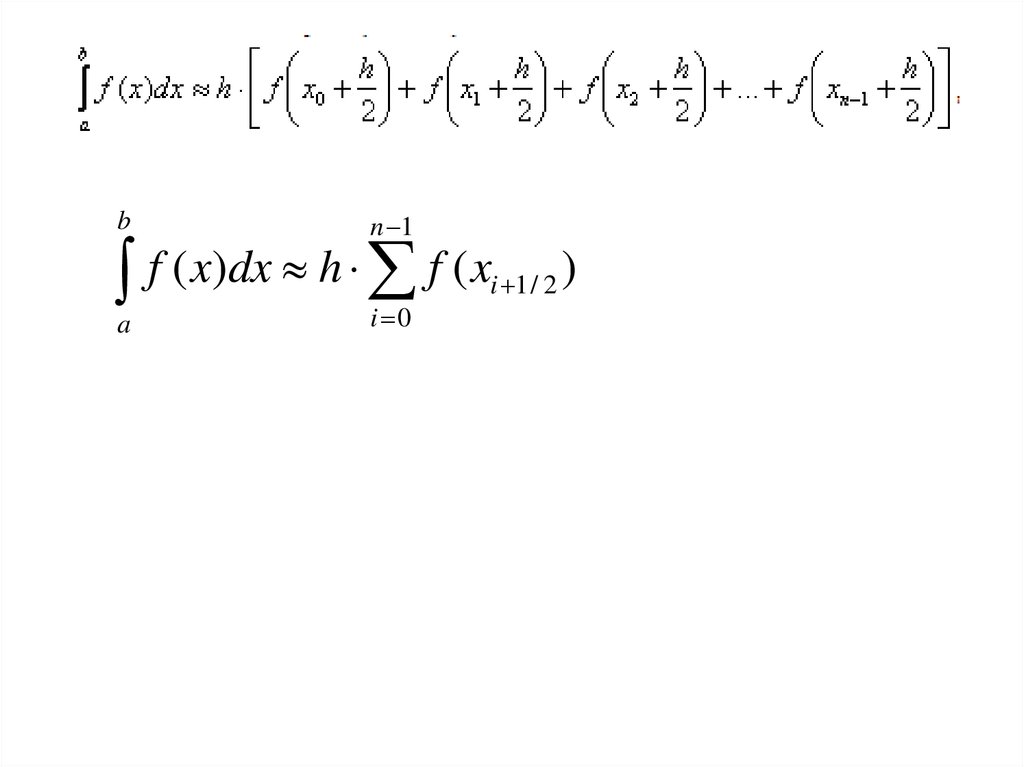





 Математика
Математика








