Властивості моделей. Симетрія у фізиці

1. Властивості моделей

Модель є замінником реального об'єкта і володіє, принаймні, двома властивостями:
а) вона відображає ті властивості об'єкта, які істотні для даного дослідження;
б) завжди простіше об'єкта.
Модель повинна бути:
- адекватною;
- надійною;
- простою і зрозумілою користувачу;
- спрямованою на досягнення поставлених цілей дослідження;
- зручною у використанні (ергономічною);
- функціонально повною з точки зору можливостей вирішення головних завдань;
- адаптивною, що дозволяє легко переходити до інших модифікацій або оновлювати дані;
- допускаючою зміни (в процесі експлуатації вона може ускладнюватися).
Формою графічного представлення інформації про модельовану систему можуть бути [6]:
- операторно-структурні схеми, прийняті в ТАУ;
- функціональні та принципові схеми різних фізичних пристроїв;
- кінематичні схеми механізмів;
- сигнальні графи (SFG);
- графи зв'язків або зв'язані графи (BG);
- блок-схеми алгоритмів та інші графічні моделі.

2. Симетрія у фізиці

Принцип: — Закон збереження:
Однорідність часу
—…енергії
Ізотропність часу
—…парності
Однорідність простору —…імпульсу
Ізотропність простору
—…моменту імпульсу
Інваріантність
— … енергії-імпульса,
у чотиривимірному просторі-часі

3. Рівняння Максвелла

ρ — щільність стороннього електричного заряду (в СІ — Кл/м³);
j — щільність електричного струму (струму провідності) (в СІ — А/м²);
c — швидкість светла в вакуумі (299 792 458 м/с);
E — напруженість електричного поля (в СІ — В/м);
H — напруженість магнітного поля (в СІ — А/м);
D — електрична індукція (в СІ — Кл/м²);
B — магнітна індукція (в СІ — Тл = Вб/м²);
— диференційний оператор набла, при цьому:
× — означає ротор вектора,
· — означає дівергенцію вектора.

4. Фундаментальна система рівнянь напівпровідника (ФСР) складається з двох рівнянь переносу, двох рівнянь безперервності та рівняння Пуассо

Фундаментальна система рівнянь напівпровідника (ФСР)
складається з двох рівнянь переносу,
двох рівнянь безперервності та рівняння Пуассона
1 J n n n0 n
q x
n
t
n
J n q n nE qDn
x
p
J p q p pE qD p
x
r 0
E
q p n N D N A
x
де J - щільність струму;
q - елементарний заряд;
μ - рухливість носіїв;
E - напруженість електричного поля;
D - коефіцієнт дифузії;
n і p - концентрація електронів і дірок відповідно;
τ - час життя носіїв заряду;
εr - відносна діелектрична проникність;
ε0 - електрична постійна;
N - концентрація домішок (D - донорна, A - акцепторна).
1 J p p p 0 p
q x
p
t

5. Модель “ящика”

Зовнішні (Q)
Вхідні (X)
Внутрішні (W)
Вихідні (Y)
Y=F(X,Q) – чорний ящик
Y=F(W,X,Q) – білий ящик
Y=F(W,X,Q, u) – білий ящик із невизначеністю

6. Моделі пасивних елементів

iR
uR
R
iC C
duC
dt
diL
uL L
dt
а
б
в
Еквівалентні схеми: а – резистора, б – конденсатора,
в – котушки індуктивності

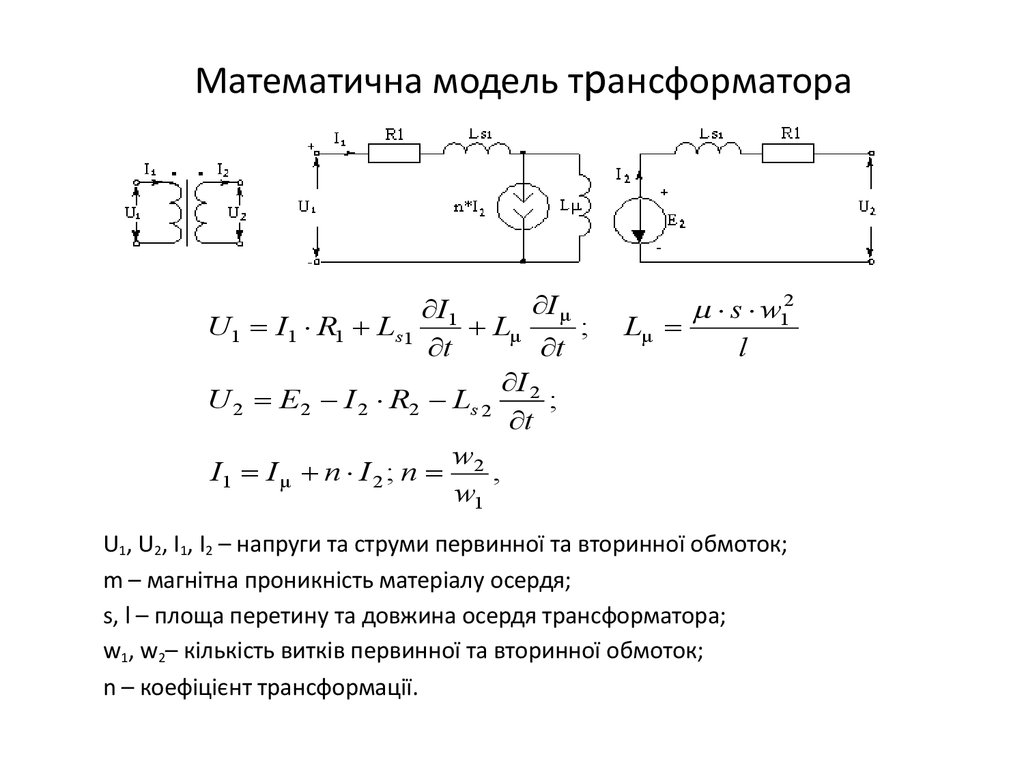
7. Математична модель трансформатора

I μ
I
U1 I1 R1 Ls1 1 Lμ
;
t
t
I
U 2 E2 I 2 R2 Ls 2 2 ;
t
w
I1 I μ n I 2 ; n 2 ,
w1
s w12
Lμ
l
U1, U2, I1, I2 – напруги та струми первинної та вторинної обмоток;
m – магнітна проникність матеріалу осердя;
s, l – площа перетину та довжина осердя трансформатора;
w1, w2– кількість витків первинної та вторинної обмоток;
n – коефіцієнт трансформації.

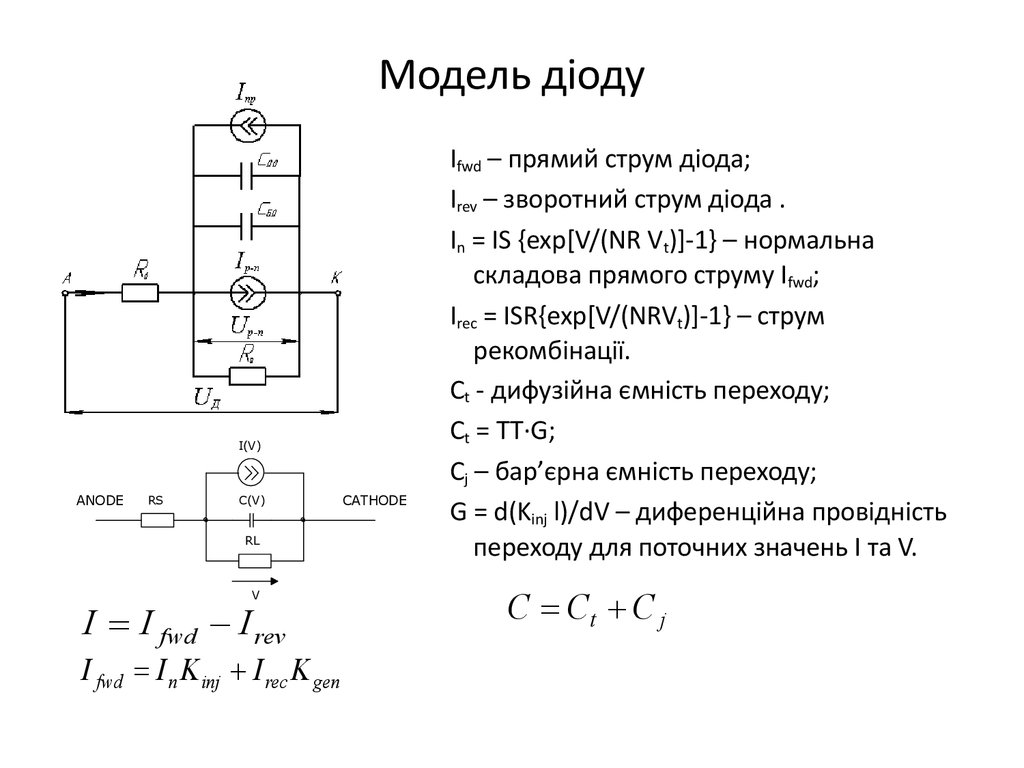
8. Модель діоду

I(V)
ANODE
RS
C(V)
RL
V
I I fwd I rev
I fwd I n K inj I rec K gen
CATHODE
Ifwd – прямий струм діода;
Irev – зворотний струм діода .
In = IS {exp[V/(NR Vt)]-1} – нормальна
складова прямого струму Ifwd;
Irec = ISR{exp[V/(NRVt)]-1} – струм
рекомбінації.
Сt - дифузійна ємність переходу;
Ct = TT·G;
Cj – бар’єрна ємність переходу;
G = d(Kinj l)/dV – диференційна провідність
переходу для поточних значень I та V.
C Ct C j

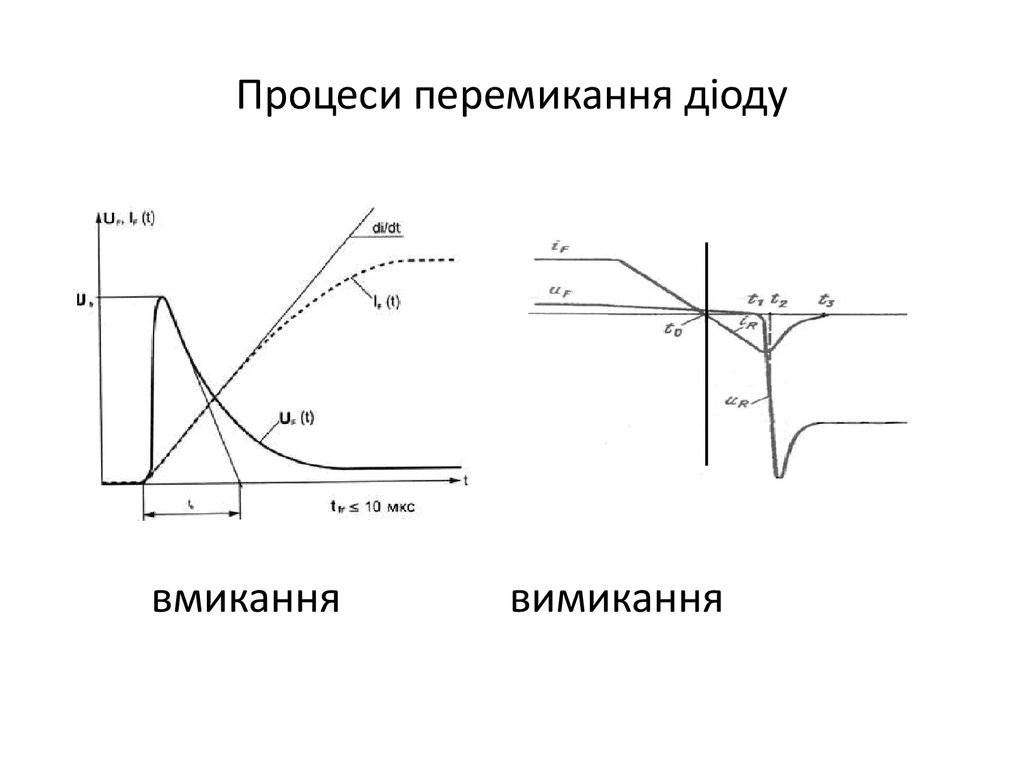
9. Процеси перемикання діоду

вмикання
вимикання

10. Параметри діоду

Максимально допустимі значення (не повинні бути перевищені):
URRM – максимальна повторювана імпульсна зворотна напруга синусоїдальної форми на частоті 50 Гц;
URSM – неповторювана імпульсна зворотна напруга при певній температурі Tj (наприклад, від -60 оС до +75
о
С); тривалість URSM короткочасна (десятки мкс), імпульси зумовлені грозовим розрядом, або перехідними
процесами в зовнішній мережі;
IRRM – амплітудне значення повторюваного імпульсного зворотного струму при температурі структури (Tj =
175 оС) і зворотній напрузі UR = URRM ;
IFAV – максимально допустимий середній прямий струм за період при певному значенні температури
корпусу приладу;
IFRMS – діюче значення прямого струму діоду;
IFSM – ударний неповторюваний прямий струм, що нагріває напівпровідникову структуру до температури
вище допустимої;
– захисний показник: значення інтегралу від квадрату ударного струму діода за час його протікання tp . Для
захисту СНП при короткому замиканні у навантаженні перетворювача, захисний показник запобіжника має
бути нижче захисного показника приладу, який він захищає;
Tj – температура напівпровідникової структури, визначається експериментально, або шляхом виконання
розрахунків по тепловим параметрам приладу і охолоджувача, та втратам потужності в приладі.
Електричні характеристики:
UFM – імпульсна пряма напруга, найбільше миттєве значення основної напруги на діоді, зумовлене
імпульсним струмом;
UF0 – порогова пряма напруга, близька до контактної різниці потенціалів;
rF – динамічний опір у відкритому стані;
Q rr – заряд зворотного відновлення, витікає при перемиканні із заданого струму IF на задану зворотну
напругу U .

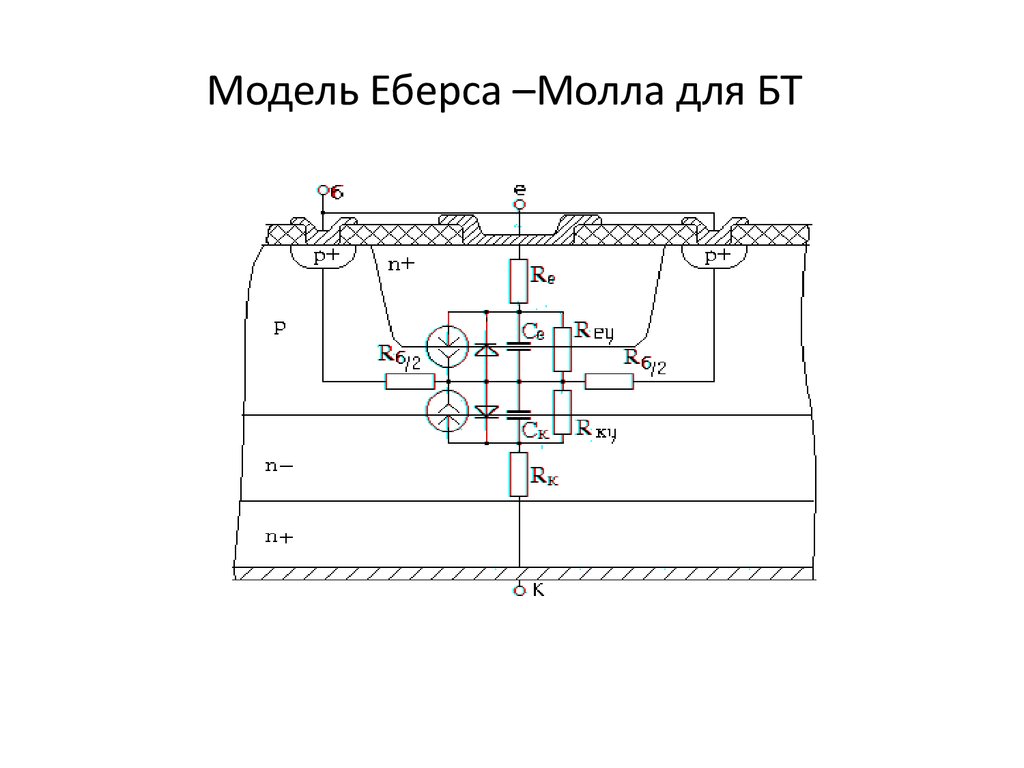
11. Модель Еберса –Молла для БТ

12.

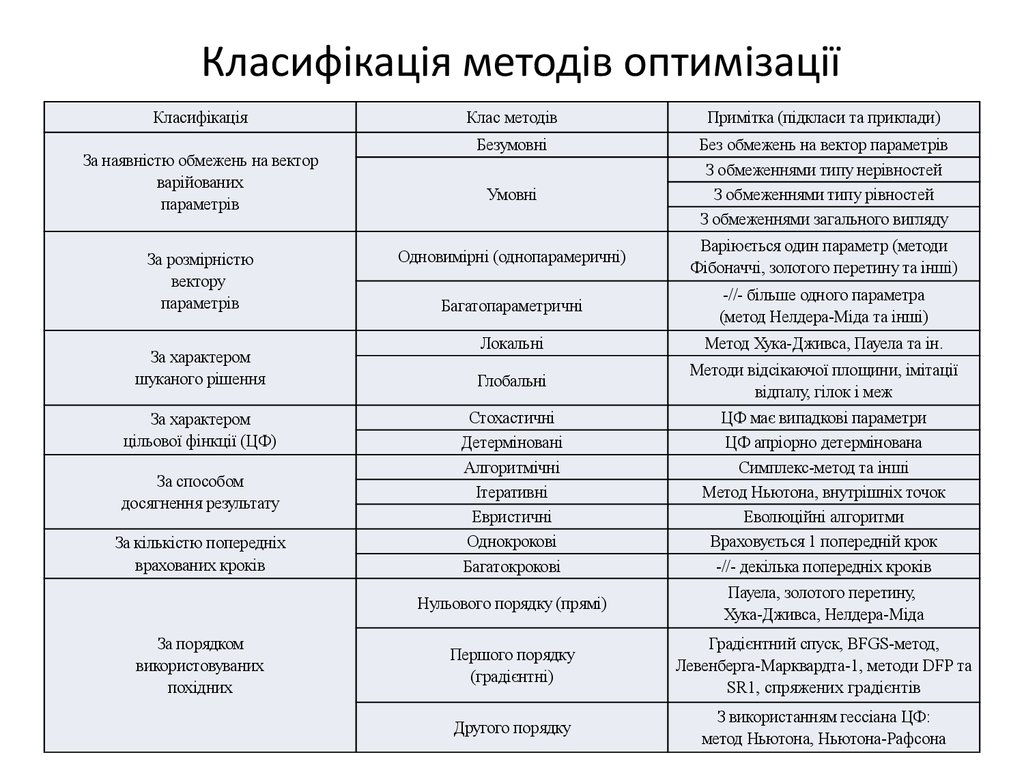
13. Класифікація методів оптимізації

Класифікація
За наявністю обмежень на вектор
варійованих
параметрів
За розмірністю
вектору
параметрів
За характером
шуканого рішення
За характером
цільової фінкції (ЦФ)
За способом
досягнення результату
За кількістю попередніх
врахованих кроків
За порядком
використовуваних
похідних
Клас методів
Примітка (підкласи та приклади)
Безумовні
Без обмежень на вектор параметрів
З обмеженнями типу нерівностей
З обмеженнями типу рівностей
З обмеженнями загального вигляду
Умовні
Одновимірні (однопарамеричні)
Варіюється один параметр (методи
Фібоначчі, золотого перетину та інші)
Багатопараметричні
-//- більше одного параметра
(метод Нелдера-Міда та інші)
Локальні
Метод Хука-Дживса, Пауела та ін.
Глобальні
Методи відсікаючої площини, імітації
відпалу, гілок і меж
Стохастичні
Детерміновані
Алгоритмічні
Ітеративні
Евристичні
Однокрокові
Багатокрокові
ЦФ має випадкові параметри
ЦФ апріорно детермінована
Симплекс-метод та інші
Метод Ньютона, внутрішніх точок
Еволюційні алгоритми
Враховується 1 попередній крок
-//- декілька попередніх кроків
Нульового порядку (прямі)
Пауела, золотого перетину,
Хука-Дживса, Нелдера-Міда
Першого порядку
(градієнтні)
Градієнтний спуск, BFGS-метод,
Левенберга-Марквардта-1, методи DFP та
SR1, спряжених градієнтів
Другого порядку
З використанням гессіана ЦФ:
метод Ньютона, Ньютона-Рафсона

14.

15. Можливості CAE і CAS

CAE (Computer Aided Engineering) системи дозволяють досліджувати системи
на макрорівні, тобто аналізувати та оптимізувати систему із ціллю прийняття
рішення щодо топології (структурний підхід) та функціональних можливостей
в цілому (системний підхід). На даний момент існує багато програм САЕ, які
дозволяють моделювати ДС різної природи (біологічні, економічні, соціальні,
технічні), причому деякі є вузькоспеціалізованими, а інші – більш
універсальними:
Vensim, IThink, Dynamo, Stella, Powersim, MedModel, Arena, GPSS, Stratum,
Scilab, Berkeley Madonna, NI MATRIXX, ACSLx, Modular Modeling System (MMS),
Virtual Test Bed (VTB), JModelica.org, Yenka (Crocodile Technology),
MATLAB\Simulink, Simscape, MapleSim, Dynast, Multisim, K2.SimKernel, Jigrein,
EASY5, AMESim, Dymola, PSIM, SamSim, SimApp, SimulationX, Simplorer, VisSim,
SystemModeler, 20-sim, ПК МВТУ
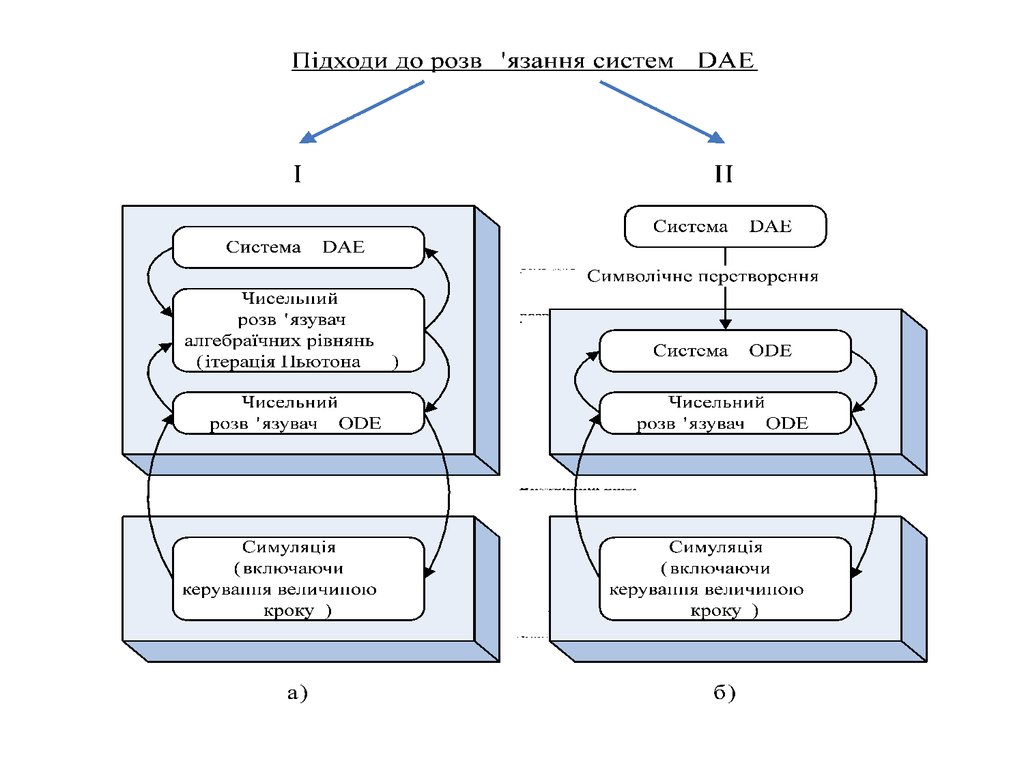
CAS (Computer Algebra System), які можуть розв’язувати диференціальні
рівняння (чисельно чи у символічній формі):
Maple, MATLAB, Mathcad, Mathematica, Maxima, SymPy, O-Matrix, SciPy, Octave,
NumPy, Python(x,y), MuPAD, Sage та інш.

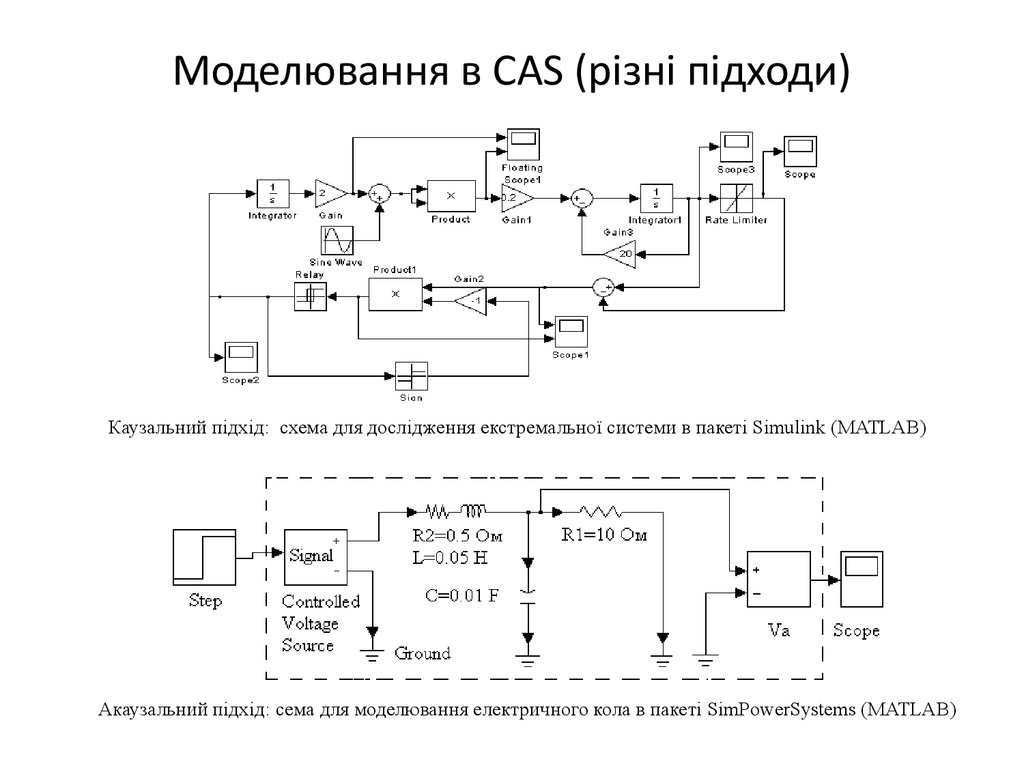
16. Моделювання в CAS (різні підходи)

Каузальний підхід: схема для дослідження екстремальної системи в пакеті Simulink (MATLAB)
Акаузальний підхід: сема для моделювання електричного кола в пакеті SimPowerSystems (MATLAB)

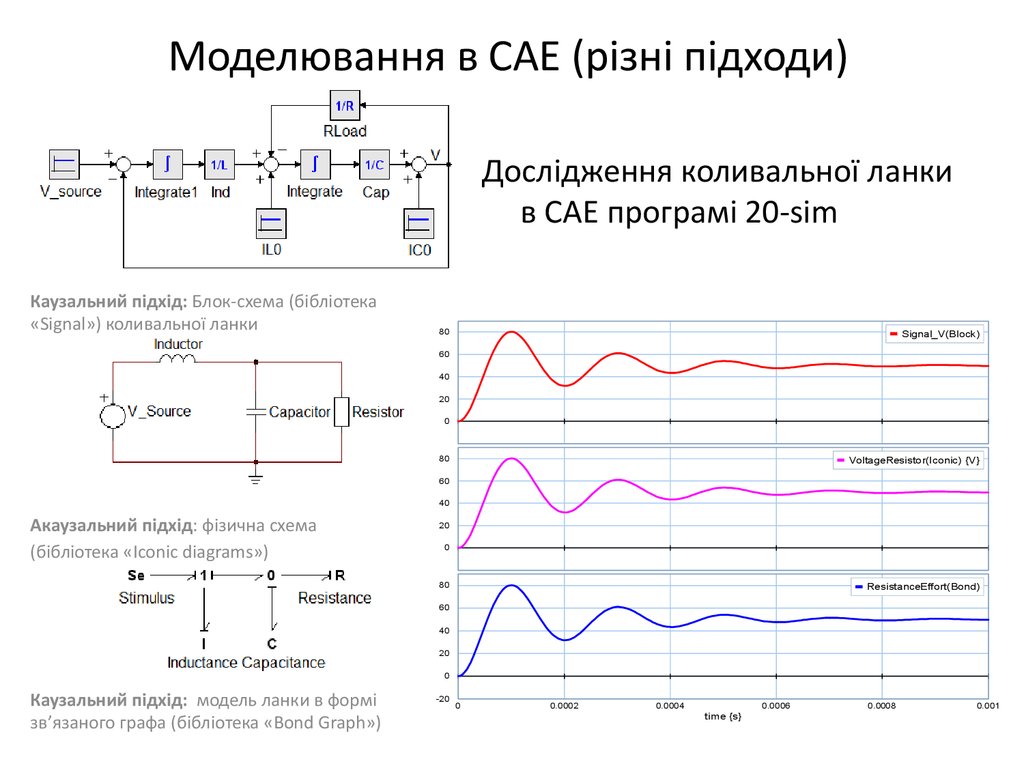
17. Моделювання в САЕ (різні підходи)

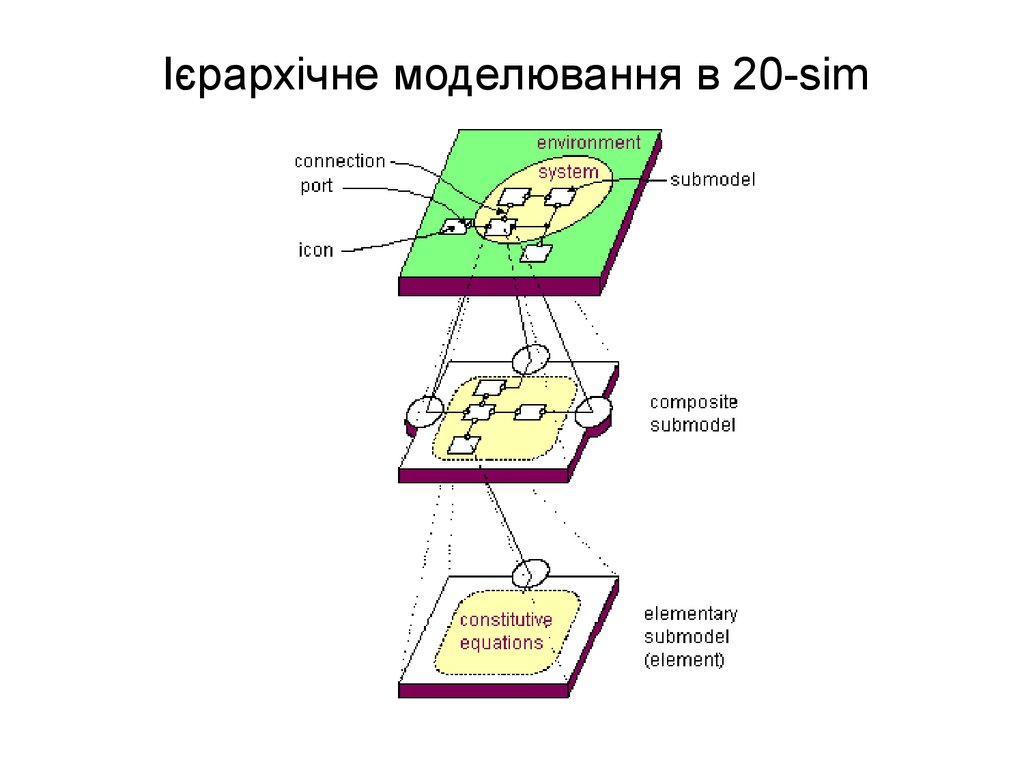
Дослідження коливальної ланки
в CAE програмі 20-sim
Каузальний підхід: Блок-схема (бібліотека
«Signal») коливальної ланки
RLC_byZX
80
Signal_V(Block)
60
40
20
0
80
VoltageResistor(Iconic) {V}
60
40
Акаузальний підхід: фізична схема
(бібліотека «Iconic diagrams»)
20
0
80
ResistanceEffort(Bond)
60
40
20
0
Каузальний підхід: модель ланки в формі
зв’язаного графа (бібліотека «Bond Graph»)
-20
0
0.0002
0.0004
0.0006
time {s}
0.0008
0.001

18. Віртуальна аналогова обчислювальна машина (квазікаузальний підхід – системний рівень в ECAD)

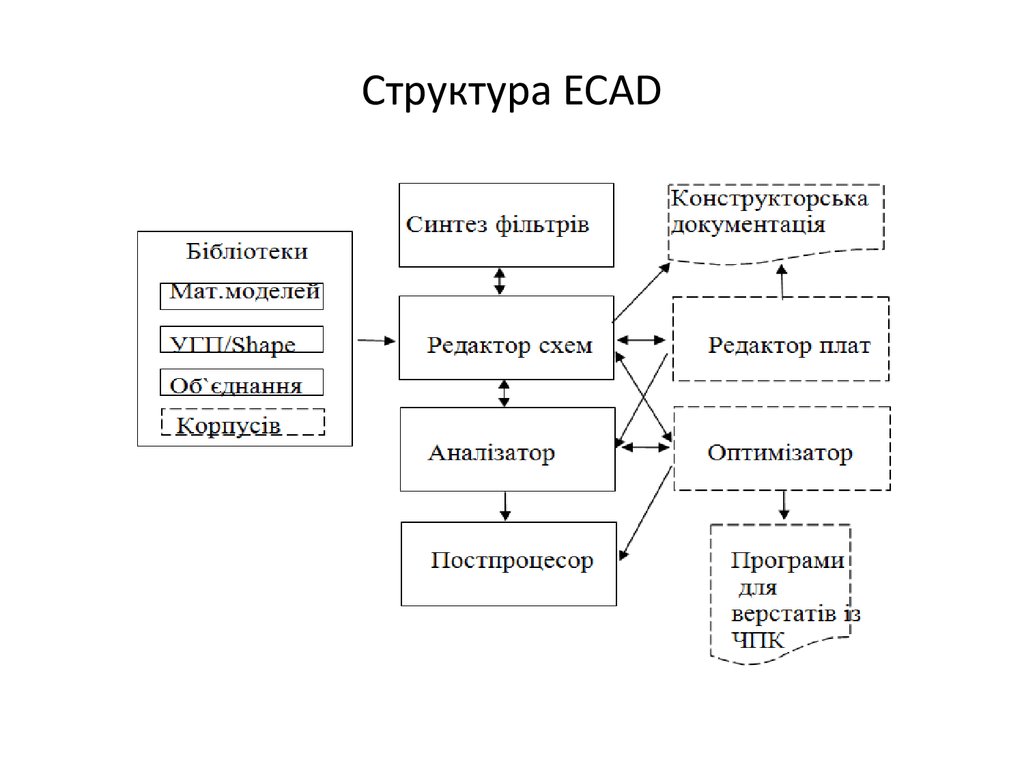
19. Квазікаузальний підхід – структурний рівень в ECAD

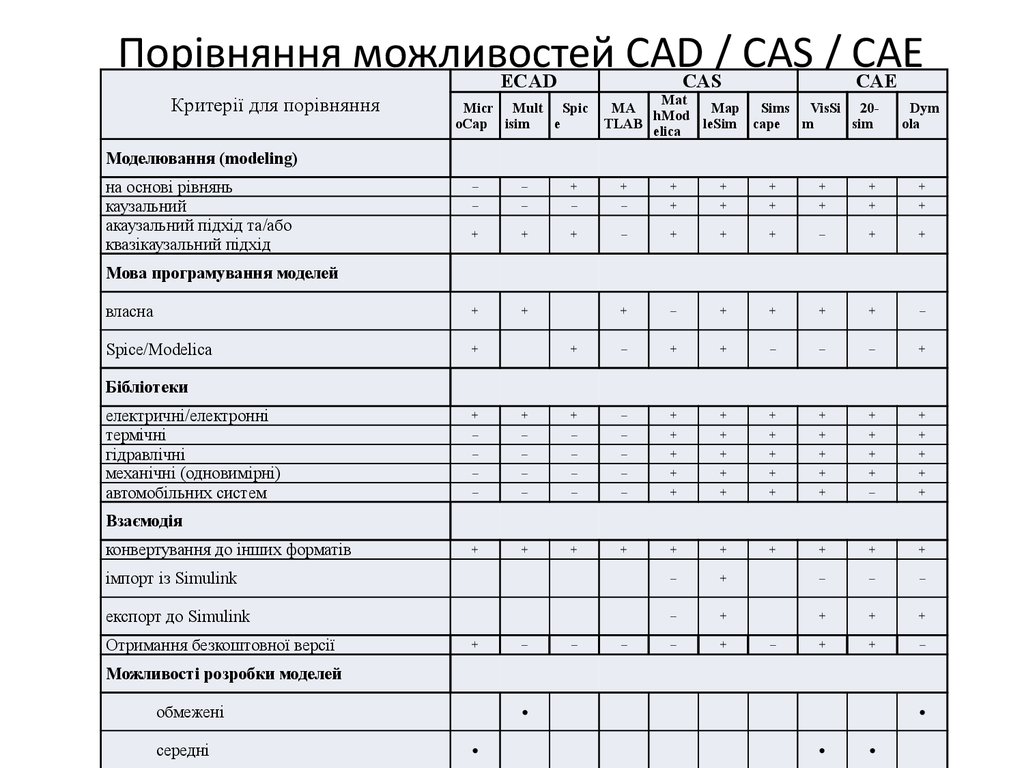
20. Порівняння можливостей CAD / САS / САЕ

ЕCAD
САS
САЕ
Критерії для порівняння
Micr Mult Spic
oCap isim
e
Mat
MA
Map Sims VisSi 20hMod
TLAB
leSim cape
m
sim
elica
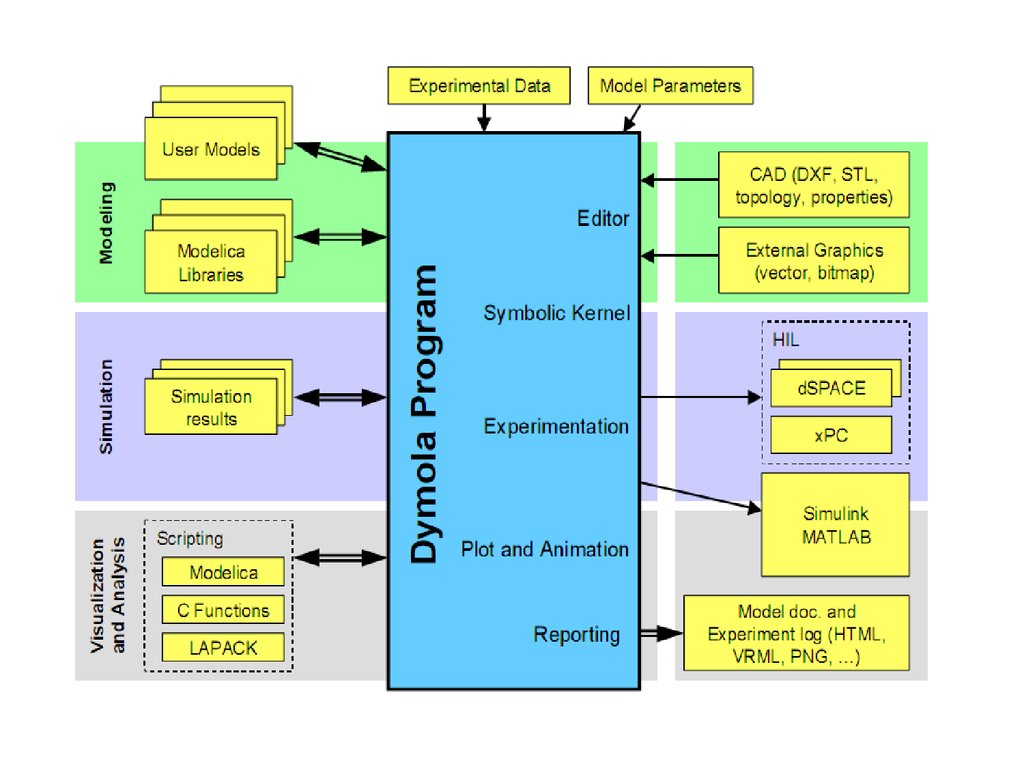
Dym
ola
Моделювання (modeling)
на основі рівнянь
каузальний
акаузальний підхід та/або
квазікаузальний підхід
–
–
+
+
+
+
+
+
+
+
–
–
–
–
+
+
+
+
+
+
+
+
+
–
+
+
+
–
+
+
власна
+
+
+
–
+
+
+
+
–
Spice/Modelica
+
+
–
+
+
–
–
–
+
Мова програмування моделей
Бібліотеки
електричні/електронні
термічні
гідравлічні
механічні (одновимірні)
автомобільних систем
+
+
+
–
+
+
+
+
+
+
–
–
–
–
+
+
+
+
+
+
–
–
–
–
+
+
+
+
+
+
–
–
–
–
+
+
+
+
+
+
–
–
–
–
+
+
+
+
–
+
+
+
+
+
+
+
+
+
+
+
імпорт із Simulink
–
+
–
–
–
експорт до Simulink
–
+
+
+
+
–
+
+
+
–
Взаємодія
конвертування до інших форматів
Отримання безкоштовної версії
+
–
–
–
–
Можливості розробки моделей
обмежені
середні

21. САЕ VisSim та додаткові модулі

22. Структура 20-sim

23.

Ієрархічне моделювання в 20-sim

24.

25. Структура ECAD