Тунельно-резонансні явища. Інтерференційні ефекти та прилади

1. Тунельно-резонансні явища. Інтерференційні ефекти та прилади.

2.

Резонансне тунелювання
Квантова яма між двох дуже широких бар'єрів добре вивчена.
En
стани електронів в ямі є визначеними і характеризуються
енергіями
En
Коли бар'єри звужуються – маємо невизначені стани оскільки електрон може
тунелювати через бар'єри і покинути яму
a
TR
TL
left lead
well
right
lead
h/ t
E1
E1
t – час життя електрона в ямі

3.

Транспорт через гетероструктуру
- Хвильові вектори руху частинки в передбар'єрній ( z £ 0) та підбар'єрній ( z > 0) областях
Vb
0
z
k = 2m * E / h2 , z £ 0
kb = 2m * ( E - V0 ) / h2 , z > 0
- Хвильова функція частинки
ì Aeikz + Be - ikz ,
y ( z ) = í ik z
- ikb z
b
Ce
+
De
,
î
z£0
z³0

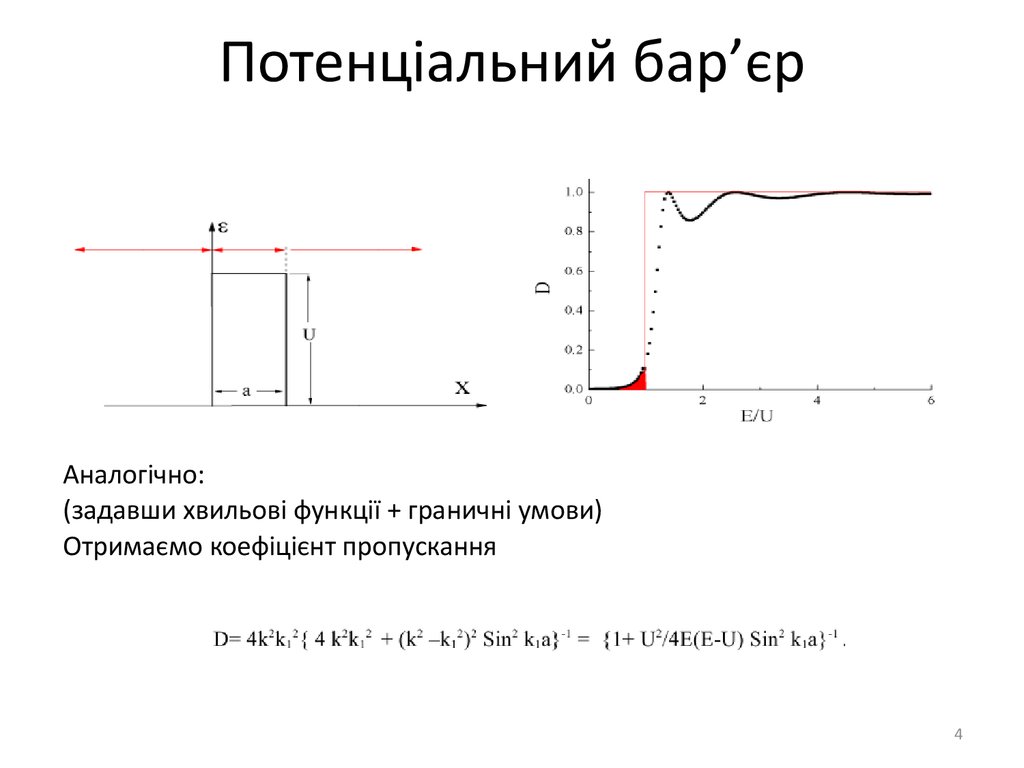
4. Потенціальний бар’єр

Аналогічно:
(задавши хвильові функції + граничні умови)
Отримаємо коефіцієнт пропускання
4

5.

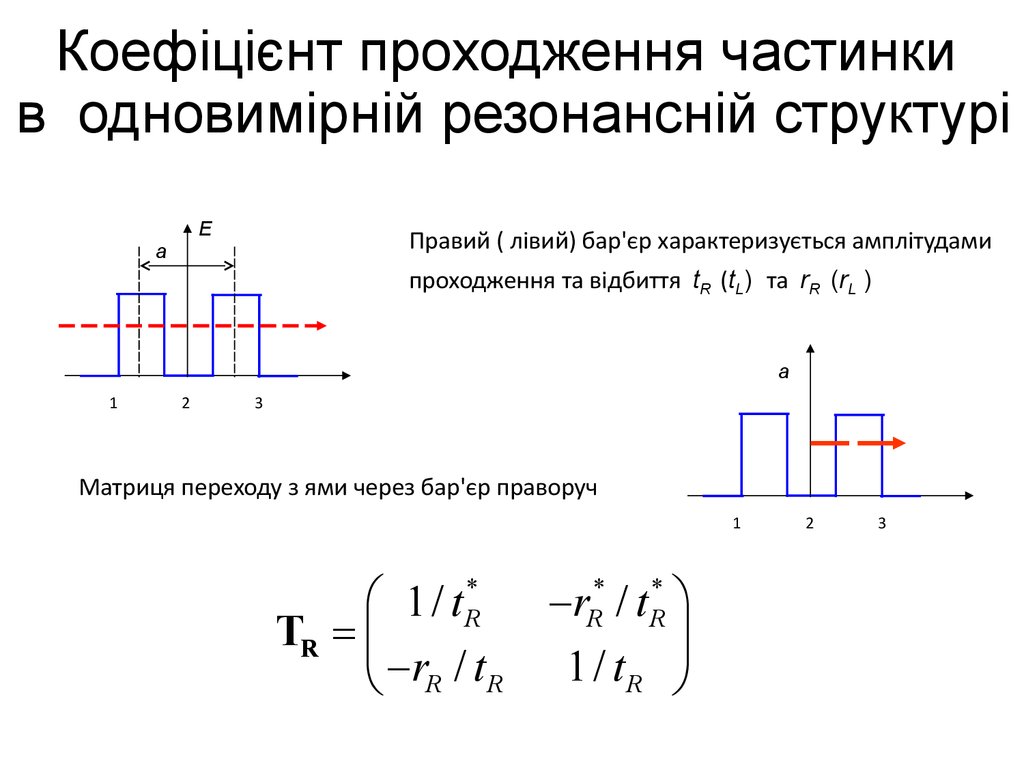
Коефіцієнт проходження частинки
в одновимірній резонансній структурі
E
Правий ( лівий) бар'єр характеризується амплітудами
a
проходження та відбиття tR (tL) та rR (rL )
a
1
2
3
Матриця переходу з ями через бар'єр праворуч
1
æ 1 / t R*
TR = ç
è - rR / t R
-r / t ö
÷
1 / tR ø
*
R
*
R
2
3

6.

Для значень енергії далеких від резонансу можна фазовий фактор sin 2 (j / 2)
замінити його середньою величиною ½ , і отримати оцінку для коефіцієнту
проходження через двобар’єрну структуру
T (TLTR)/2 .
Тривіальний результат – коефіцієнт проходження через дві перешкоди
є добутком коефіцієнтів переходу через кожну з перешкод.
TL TR
TR
T
L
1
2
1
3
2
3
Квадрати модуля амплітудних коефіцієнтів проходженя та відбитя дають
коефіцієнти проходження та відбиття по потоку.
t Lt R
T=
1- | rL || rR | e 2ika + irL + irR
2
TLTR
=
1 + RR RL - | rR || rL | ( eij + e - ij )
j = 2ka + r L + r R
Використовуючи те, що
cos j = 1 - 2sin 2 j / 2 , перепишемо цю формулу у іншому вигляді.

7.

Залежність коефіцієнта тунелювання від енергії
T = Tph
1.0 T(E)
4TLTR
( TL + TR )
2
é æ E - E ph ö 2 ù
T ( E ) Tph ê1 + ç
÷ ú
êë è / 2 ø úû
/2
-1
0.5
0.0
Eph
В умовах резонансного тунелювання
2ka + r L + r R = 2np
Умова резонансного переходу через двобар'єрну область є ні
чим іншим як умовою інтерференції електронної хвилі в ямі
При резонансному тунелюванні через симетричну структуру,
коли TL = TR , коефіцієнт проходження дорівнює одиниці.
E

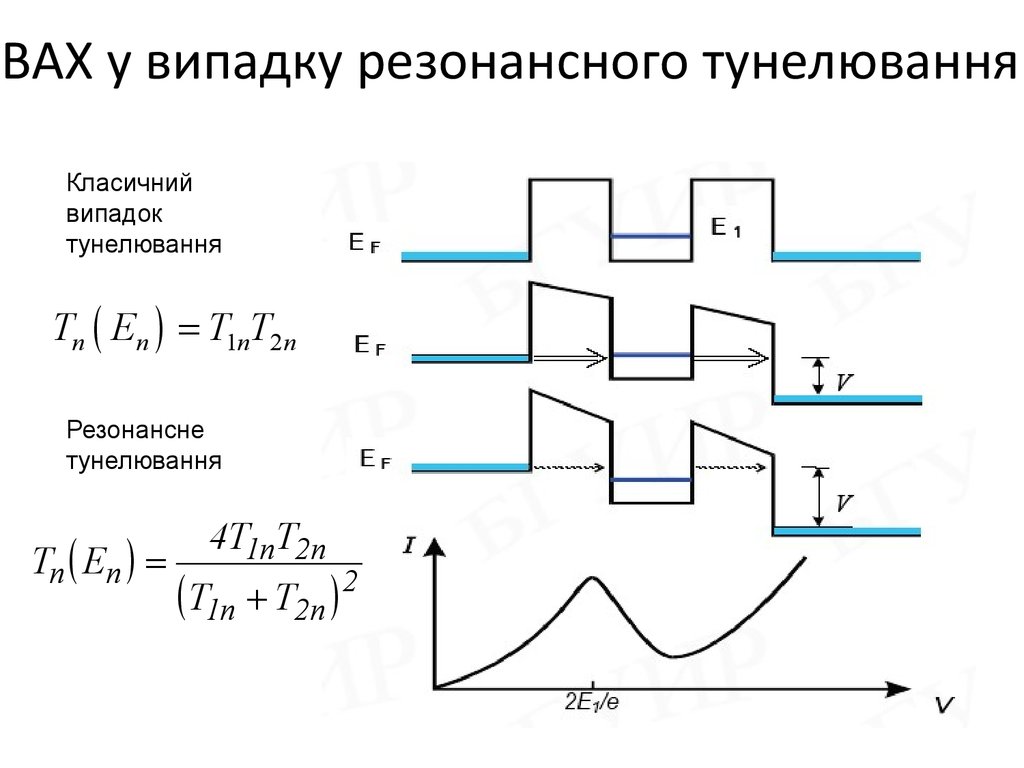
8. ВАХ у випадку резонансного тунелювання

Класичний
випадок
тунелювання
Tn ( En ) = T1nT2 n
Резонансне
тунелювання
Tn ( En ) =
4T1nT2 n
( T1n + T2 n )
2

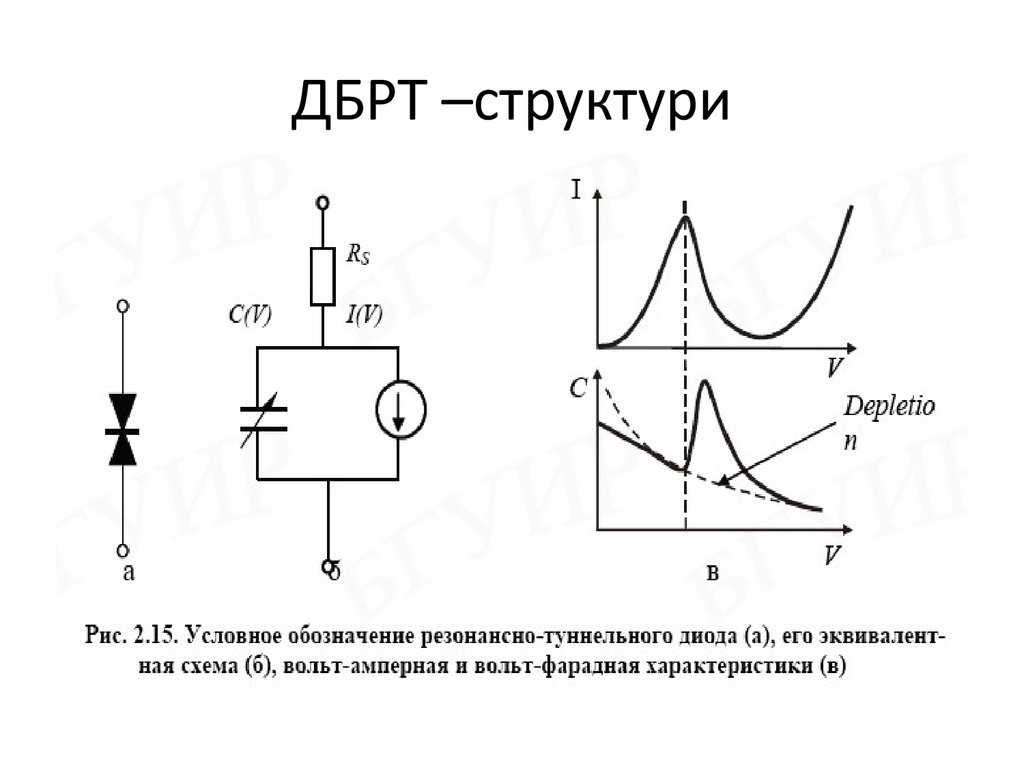
9. ДБРТ –структури

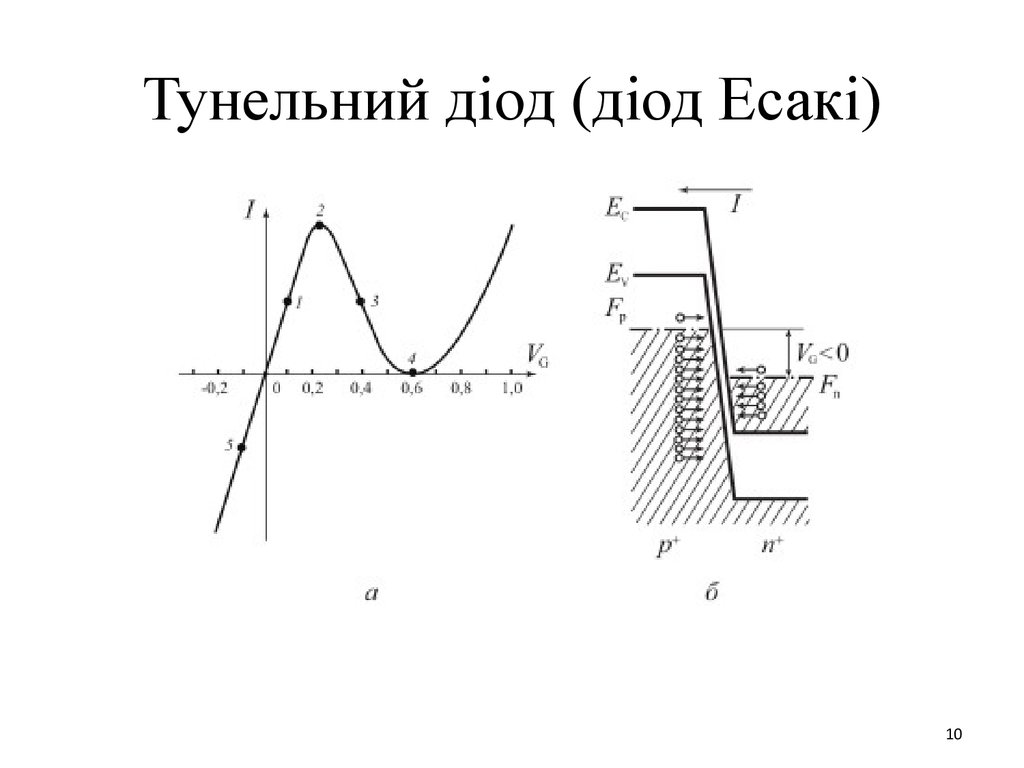
10. Тунельний діод (діод Есакі)

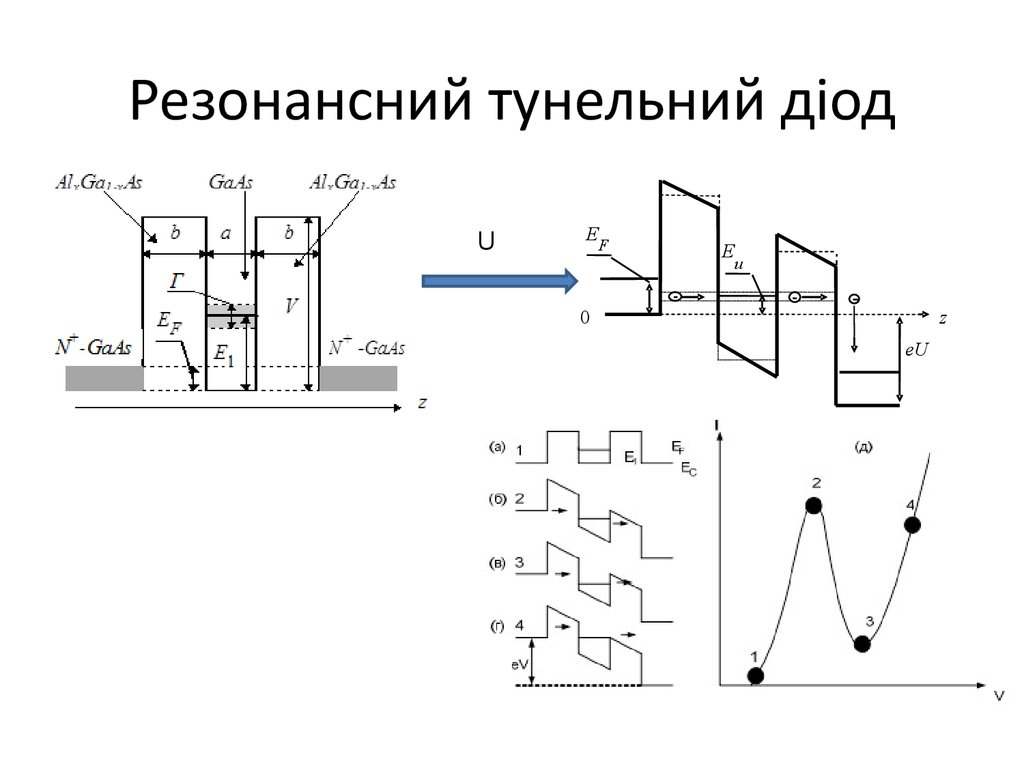
10

11. Резонансний тунельний діод

U
E
F
E
u
0
z
eU

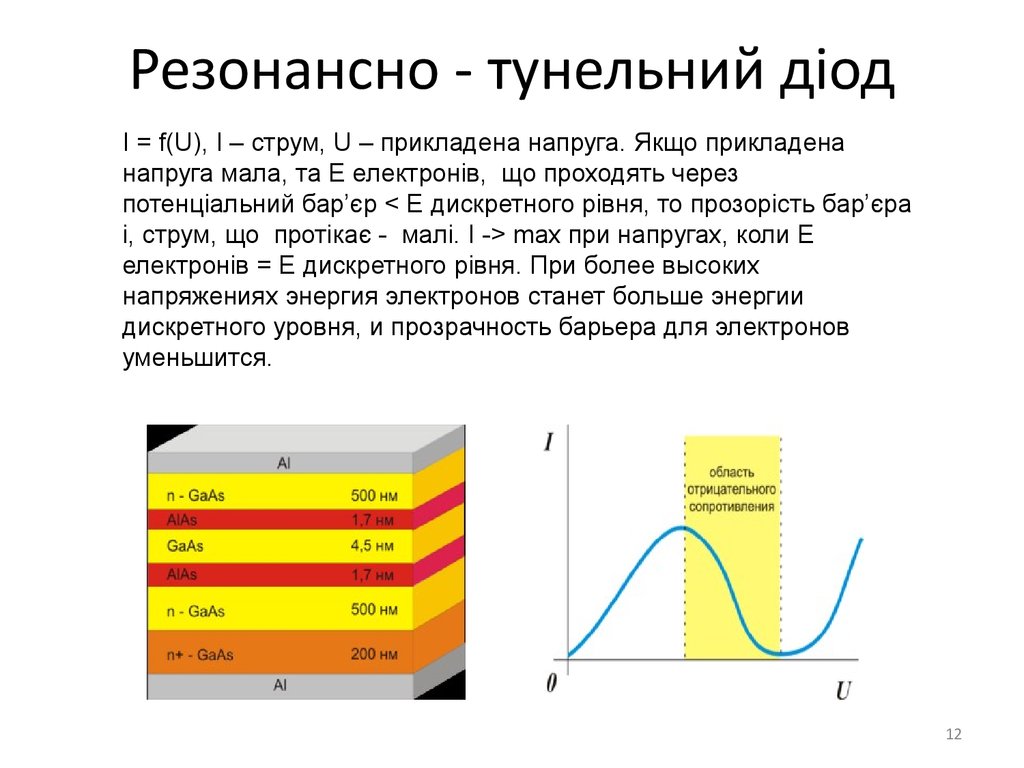
12. Резонансно - тунельний діод

I = f(U), I – струм, U – прикладена напруга. Якщо прикладена
напруга мала, та E електронів, що проходять через
потенціальний бар’єр < E дискретного рівня, то прозорість бар’єра
і, струм, що протікає - малі. I -> max при напругах, коли Е
електронів = E дискретного рівня. При более высоких
напряжениях энергия электронов станет больше энергии
дискретного уровня, и прозрачность барьера для электронов
уменьшится.
12

13.

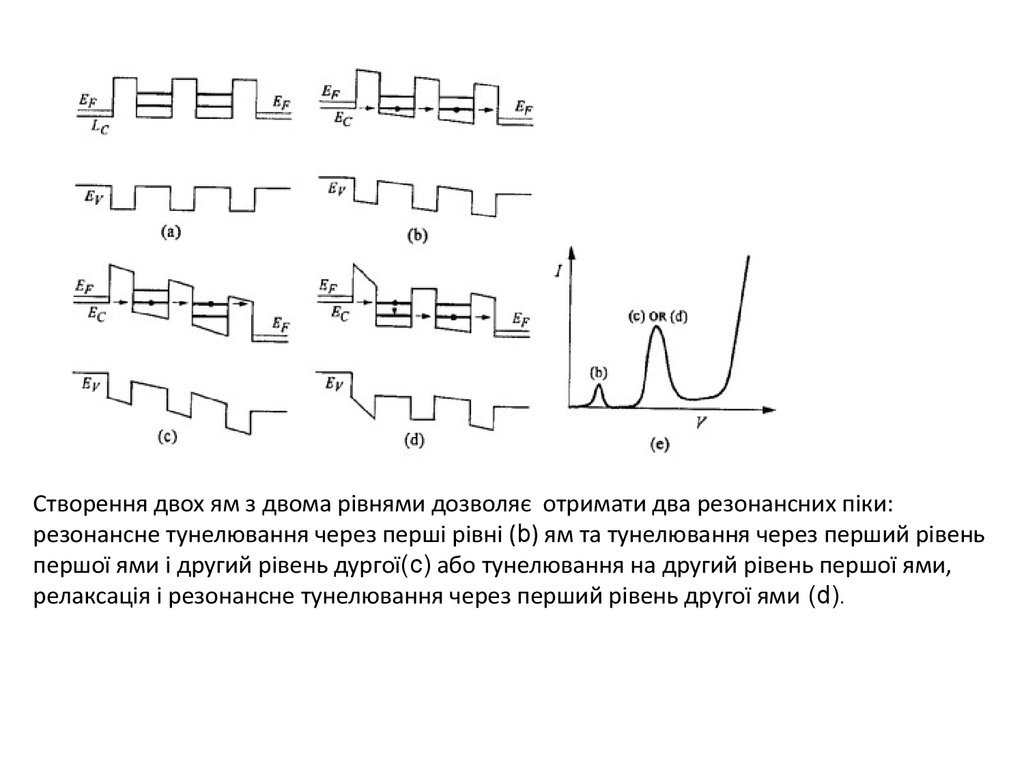
Створення двох ям з двома рівнями дозволяє отримати два резонансних піки:
резонансне тунелювання через перші рівні (b) ям та тунелювання через перший рівень
першої ями і другий рівень дургої(c) або тунелювання на другий рівень першої ями,
релаксація і резонансне тунелювання через перший рівень другої ями (d).

14.

Робоча частота генерації РТД
14

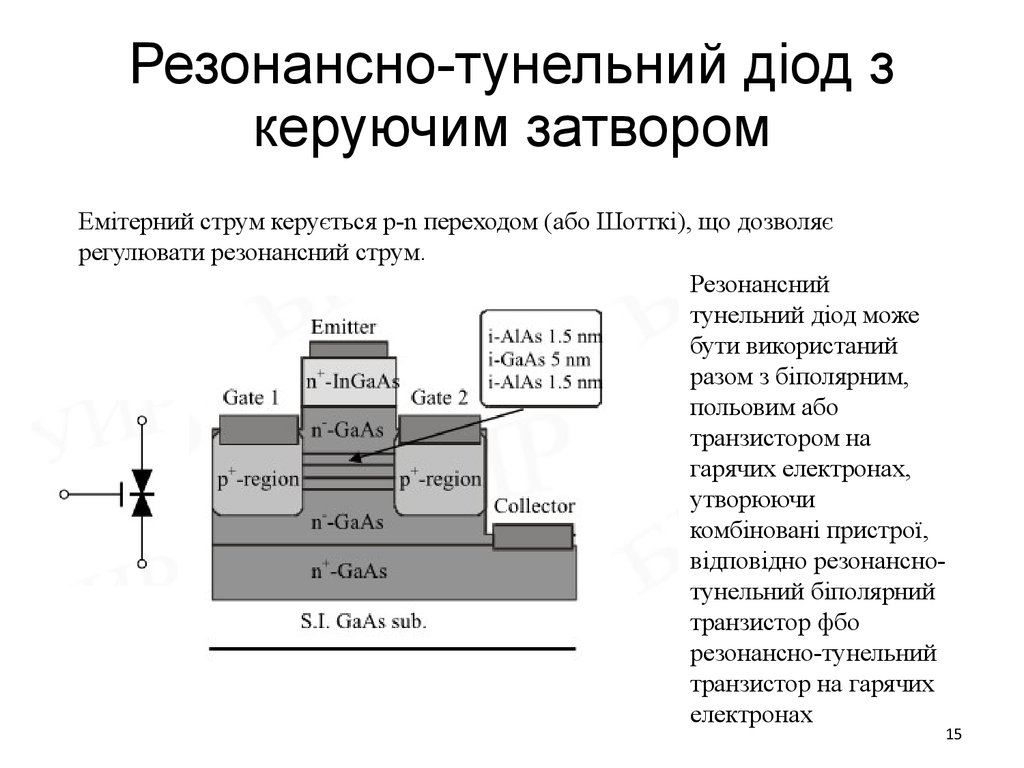
15. Резонансно-тунельний діод з керуючим затвором

Емітерний струм керується p-n переходом (або Шотткі), що дозволяє
регулювати резонансний струм.
Резонансний
тунельний діод може
бути використаний
разом з біполярним,
польовим або
транзистором на
гарячих електронах,
утворюючи
комбіновані пристрої,
відповідно резонанснотунельний біполярний
транзистор фбо
резонансно-тунельний
транзистор на гарячих
електронах
15

16. Резонансно-тунельний біполярний транзистор

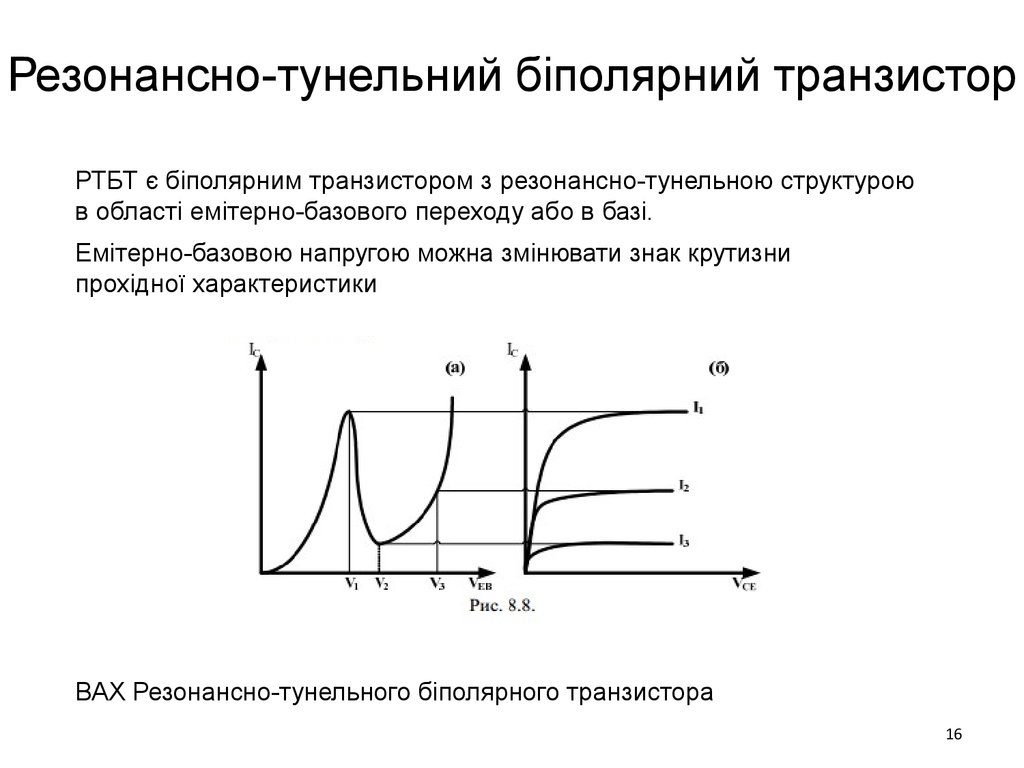
РТБТ є біполярним транзистором з резонансно-тунельною структурою
в області емітерно-базового переходу або в базі.
Емітерно-базовою напругою можна змінювати знак крутизни
прохідної характеристики
ВАХ Резонансно-тунельного біполярного транзистора
16

17. Логічні елементи на тунельно-резонансних транзисторах

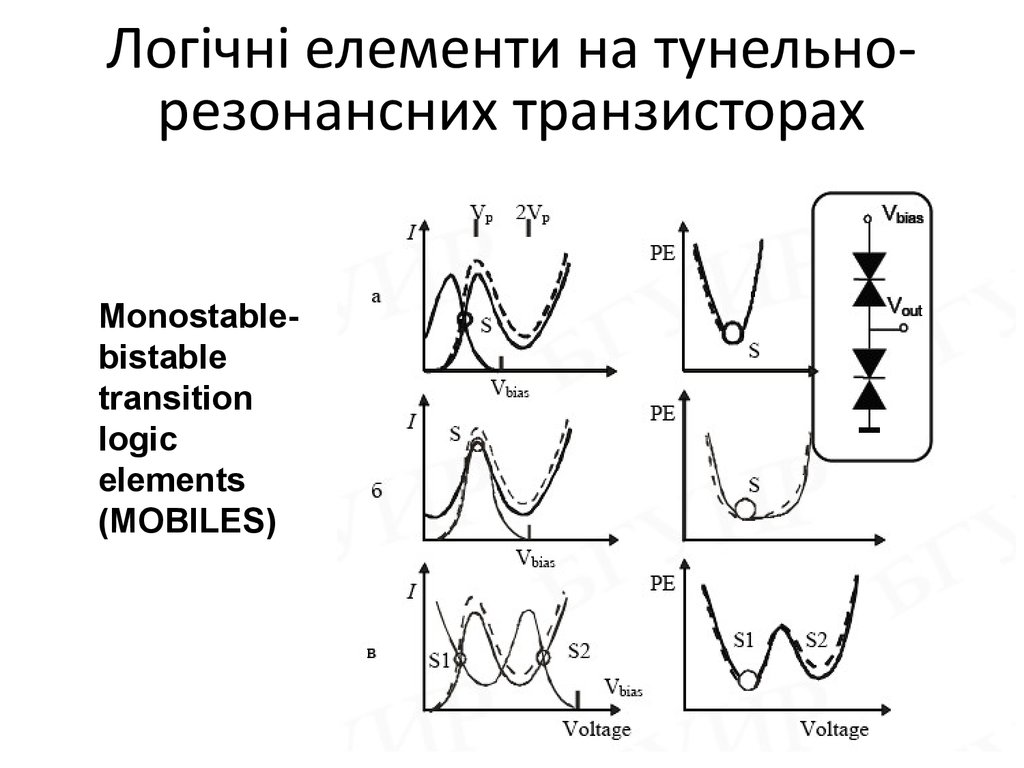
Логічні елементи на тунельнорезонансних транзисторах
Monostablebistable
transition
logic
elements
(MOBILES)

18. ДБРТ структури з блокуючими бар’єрами та їх характеристики

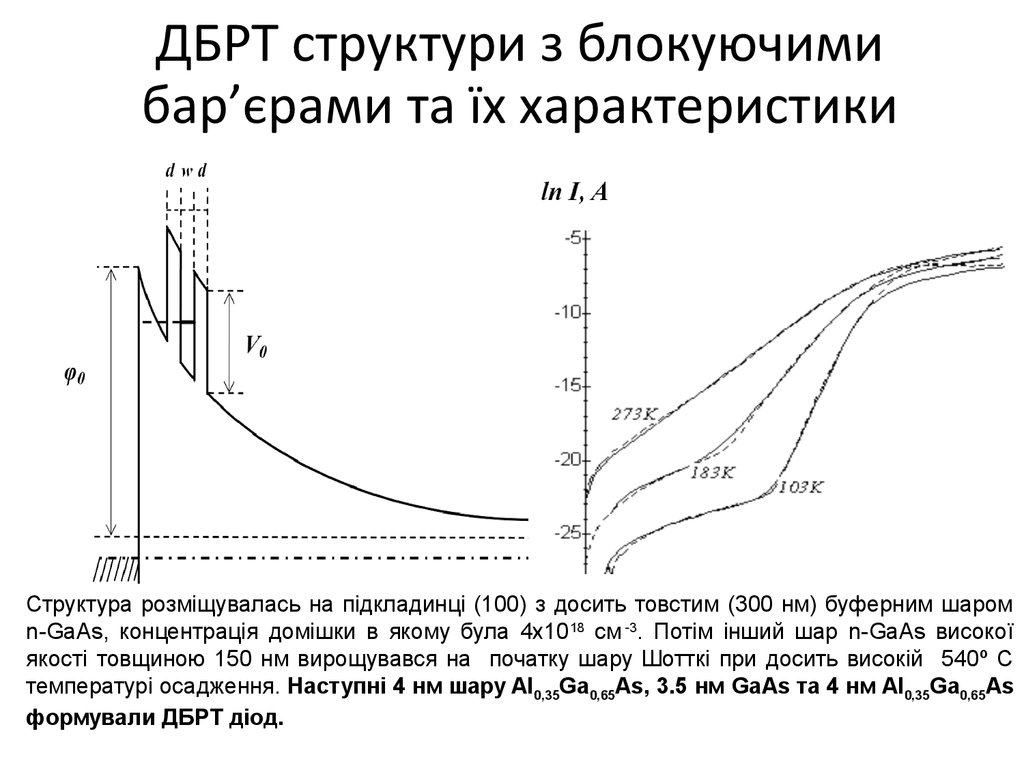
Структура розміщувалась на підкладинці (100) з досить товстим (300 нм) буферним шаром
n-GaAs, концентрація домішки в якому була 4х1018 см -3. Потім інший шар n-GaAs високої
якості товщиною 150 нм вирощувався на початку шару Шотткі при досить високій 540º С
температурі осадження. Наступні 4 нм шару Al0,35Ga0,65As, 3.5 нм GaAs та 4 нм Al0,35Ga0,65As
формували ДБРТ діод.

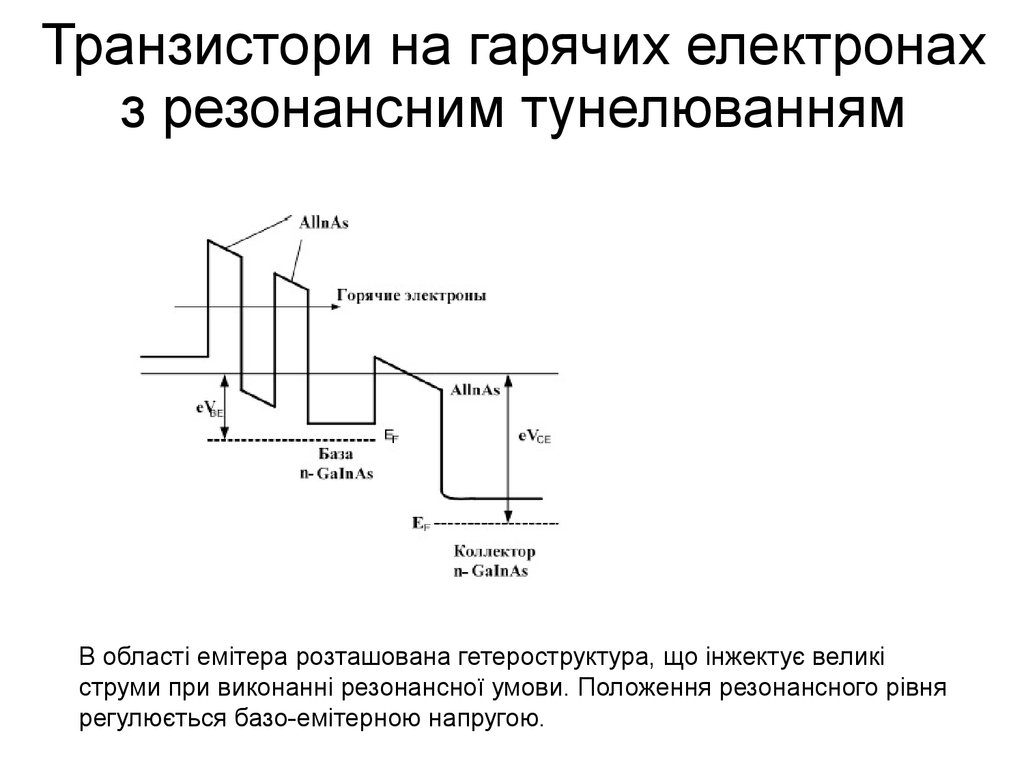
19. Транзистори на гарячих електронах з резонансним тунелюванням

В області емітера розташована гетероструктура, що інжектує великі
струми при виконанні резонансної умови. Положення резонансного рівня
регулюється базо-емітерною напругою.

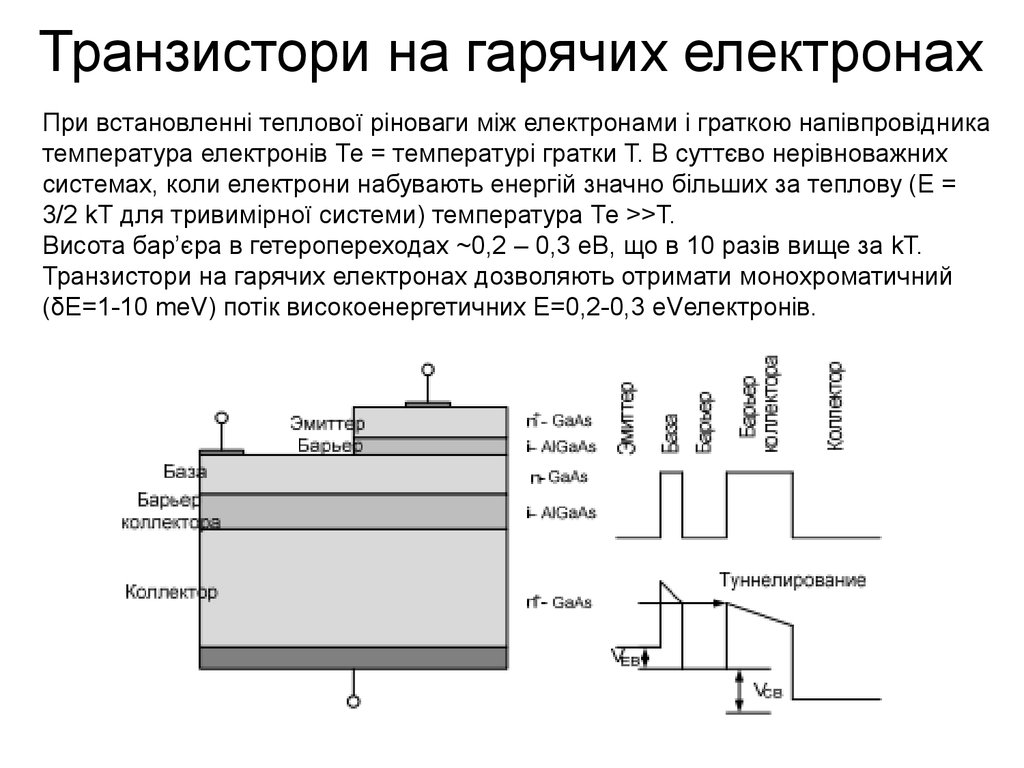
20. Транзистори на гарячих електронах

При встановленні теплової ріноваги між електронами і граткою напівпровідника
температура електронів Те = температурі гратки Т. В суттєво нерівноважних
системах, коли електрони набувають енергій значно більших за теплову (E =
3/2 kT для тривимірної системи) температура Те >>T.
Висота бар’єра в гетеропереходах ~0,2 – 0,3 еВ, що в 10 разів вище за kT.
Транзистори на гарячих електронах дозволяють отримати монохроматичний
(δE=1-10 meV) потік високоенергетичних E=0,2-0,3 eVелектронів.

21. Інтерференційні явища. Основні ідеї та співвідношення.

Y = А exp(ij )
2
2
2
W = Y1 + Y 2 = A1 + A2 =
= 4 A1 A2 Cos (j1 - j 2 )

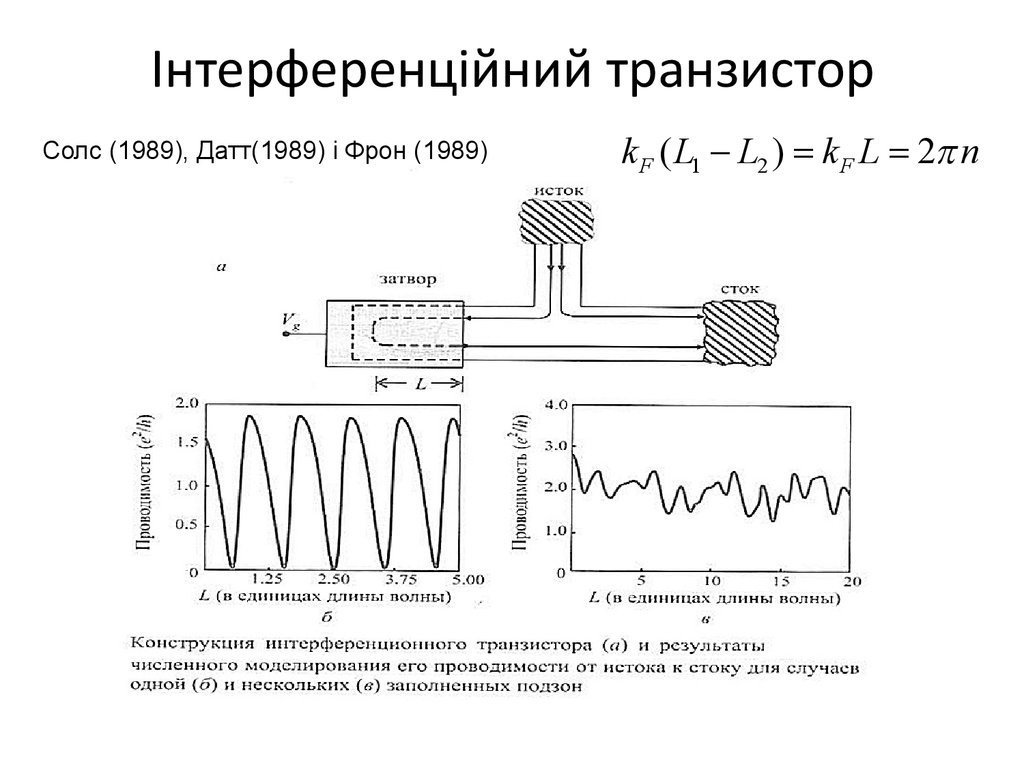
22. Інтерференційний транзистор

Солс (1989), Датт(1989) і Фрон (1989)
k F ( L1 - L2 ) = k F L = 2p n

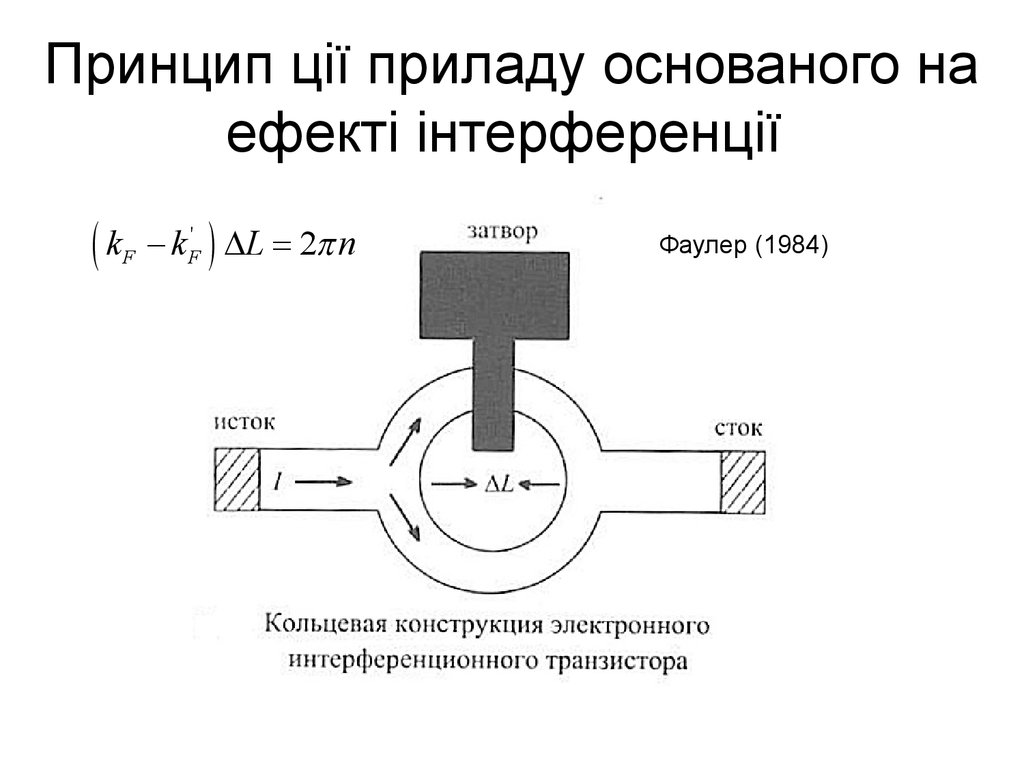
23. Принцип ції приладу основаного на ефекті інтерференції

(k
F
- k F' ) DL = 2p n
Фаулер (1984)

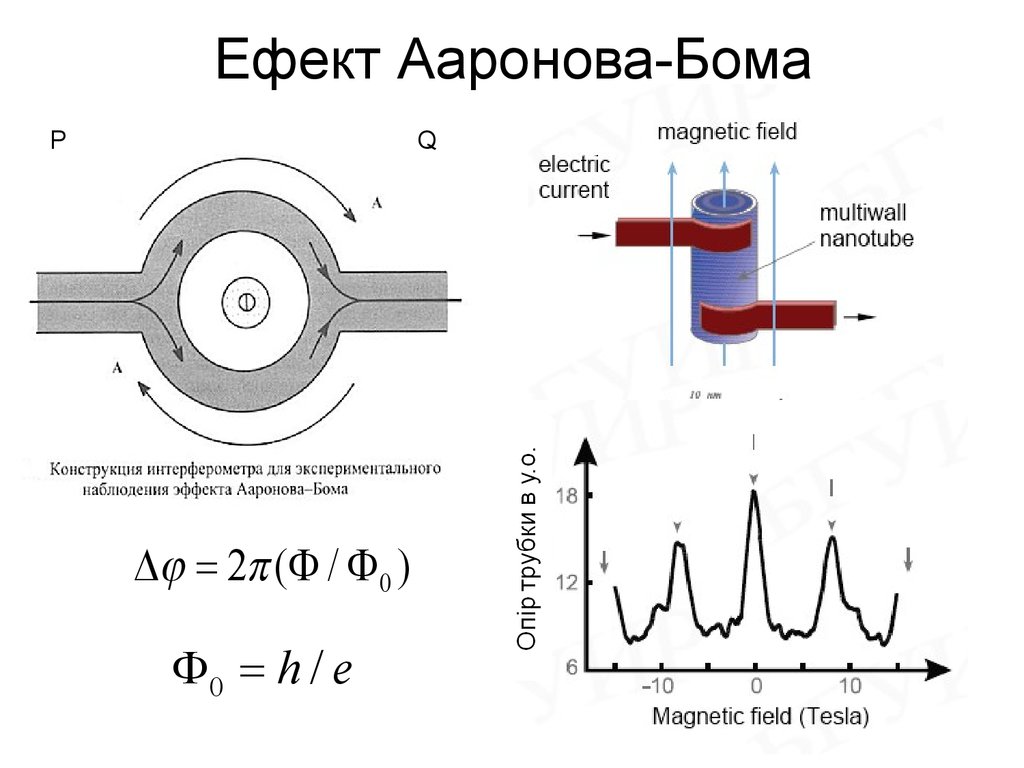
24. Ефект Ааронова-Бома

P
Q
Dj = 2p (F / F 0 )
F0 = h / e

25. Формальні співвідношення для ефекту Ааронова-Бома

r e Qr r
j (r ) = × ò A × ds
h P
2p h
F0 =
e
r r
r rù
eé
Dj = ê
A × ds A × ds ú =
ò
ò
h ë нижній маршрут
верхній маршрут
û
r r e
r
e
e
A × ds =
B × dS =
F
ò
ò
h по контуру
h по площі перерізу
h
2p F
Dj =
F0
W = Y1 + Y 2
2
2p F
= Cos (j1 - j2 ) = Cos
F0