Похожие презентации:
Теплотехника. Второе начало термодинамики. (Лекция 3)
1.
Второе началотермодинамики
Первое начало термодинамики - закон сохранения
энергии. Ничего не говорит о направлении теплообмена
между телами, приведенными в тепловой контакт.
Формулировка Клаузиуса 2-го начала термодинамики:
невозможен
процесс,
единственным
результатом
которого был бы переход тепла от тела с более низкой
температурой к телу с более высокой температурой.
Формулировка
Томсона-Планка
2-го
начала
термодинамики:
невозможен
круговой
процесс,
единственным
результатом
которого
было
бы
производство работы за счет охлаждения теплового
резервуара.
2.
Второе началотермодинамики
Второе начало устанавливает условия,
возможно превращение теплоты в работу:
при которых
1. Непрерывное получение работы за счет теплоты
возможно лишь при наличии как минимум 2-х источников
теплоты с разными температурами.
2. Невозможно осуществить цикл теплового двигателя без
переноса некоторого количества тепла от источника тепла с
более высокой температурой к источнику с более низкой
температурой.
3. В цикле тепловых двигателей теплота источника не
может быть полностью превращена в работу.
3.
Второе началотермодинамики. Энтропия
Первое начало термодинамики сформулировано
квазистатических обратимых процессов.
Второе начало термодинамики
самостоятельных положений:
состоит
из
для
двух
a) 2-й закон термодинамики для обратимых процессов или
принцип существования энтропии;
б) 2-й закон термодинамики для необратимых процессов
или принцип возрастания энтропии.
4.
Второе началотермодинамики. Энтропия
а) Для каждой термодинамической системы существует
физическая величина s (энтропия) , значение которой
зависит от состояния системы и изменение которой
происходит только под действием энергии, передаваемой в
виде теплоты.
ds = d q / T .
Статистический смысл энтропии:
Энтропия – есть мера неупорядоченности в системе.
б) Энтропия изолированной системы при неравновесных
процессах в ней увеличивается (принцип возрастания
энтропии).
5.
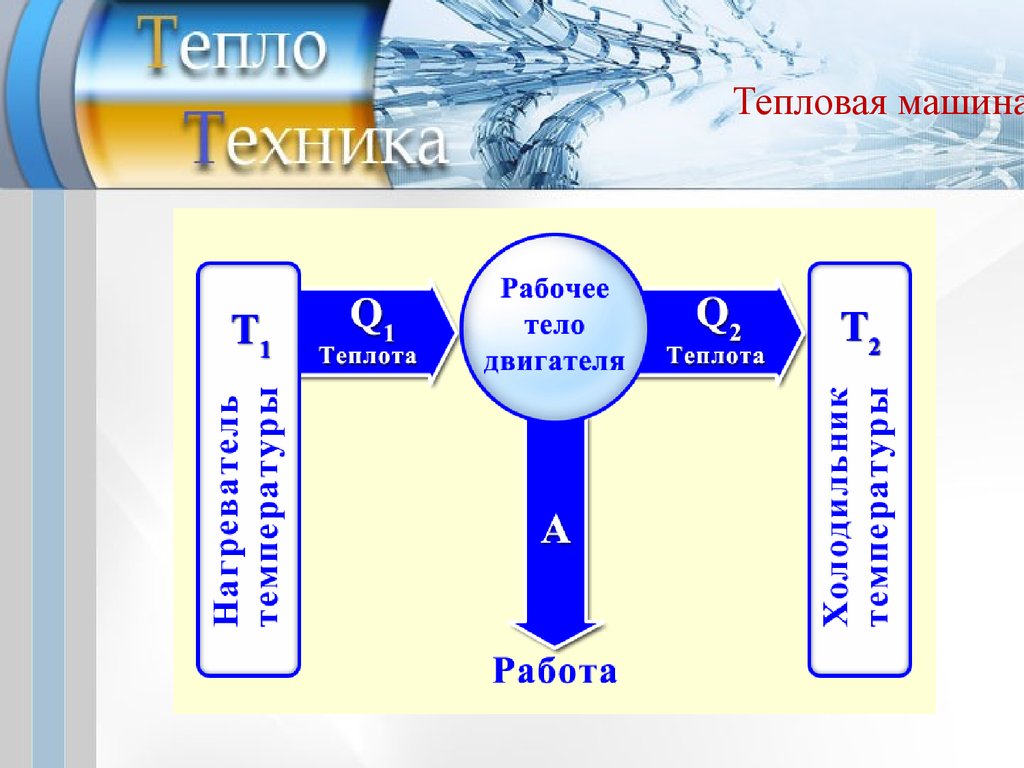
Тепловая машинаВторое начало термодинамики явилось следствием
изучения вопроса о максимальном КПД тепловых машин,
проведенным С.Карно.
Тепловая машина — устройство, преобразующее тепло
в механическую
работу (тепловой
двигатель)
или
механическую работу в тепло (холодильник). Преобразование
осуществляется
за
счёт
изменения
внутренней
энергии рабочего тела (газа или жидкости).
При работе часть тепла Q1 передается от высшего источника
теплоты (ВИТ) к рабочему телу, а затем часть энергии Q2
передается низшему источнику теплоты (НИТ), который
охлаждает машину.
6.
Тепловая машина7.
Циклы тепловыхмашин
Тепловые машины работают по замкнутому циклу.
Циклом называется замкнутый круговой процесс,
состоящий из отдельных термодинамических процессов.
Различают циклы тепловых двигателей и холодильных
машин.
8.
Тепловой двигательПрямой цикл теплового двигателя
В тепловом двигателе рабочее тело совершает положительную
работу только при расширении. Работа цикла положительна,
если круговой процесс идет по часовой стрелке.
9.
Тепловой двигательРабота цикла
1-е начало термодинамики для процесса 1а2:
q1 = Du + l1 ,
1-е начало термодинамики для процесса 2b1:
- q2 = -Du - l2 ,
q1 - q2 = l1 - l2 = lц .
10.
Тепловой двигательДля оценки эффективности цикла (степени его
совершенства) вводится понятие термического КПД - это
отношение полезной работы цикла lп к полному
количеству теплоты q1 , подведенной к рабочему телу
цикла:
ht = ln q1 = (q1 - q2 ) q1 .
Чем больше термический КПД, тем при одном и том же
количестве подведенной к циклу теплоты производится
больше работы.
11.
Холодильная машинаХолодильной
машиной
называют
непрерывно
действующую систему, осуществляющую круговые
процессы, в которой за счет подведенной извне работы
теплота от источника с низкой температурой передается к
источнику с высшей температурой.
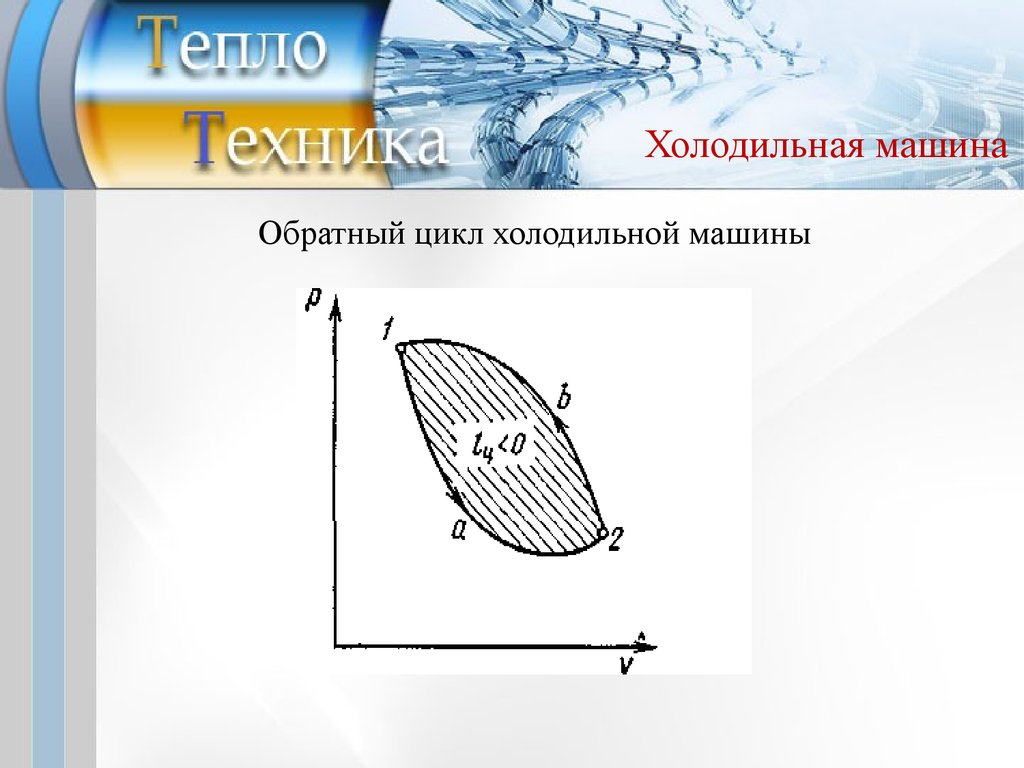
В цикле холодильных машин работа сжатия превышает
работу расширения и цикл в p–υ идет против часовой
стрелки и его называют обратным.
12.
Холодильная машинаОбратный цикл холодильной машины
13.
Второе началотермодинамики
Вещество, за счет изменения состояния которого
осуществляется цикл холодильной машины, называют
холодильным агентом. В качестве рабочих тел
(хладагентов) применяют аммиак NH3 или фреоны (их
особенность - низкая температура кипения).
Для характеристики эффективности цикла холодильной
машины вводится понятие холодильного коэффициента ,
это отношение теплоты q2, отводимой от источника с низкой
lц
температурой, к работе , затраченной
извне, на привод
машины:
= q2 lц .
14.
Идеальный цикл работытепловой машины.
Цикл Карно
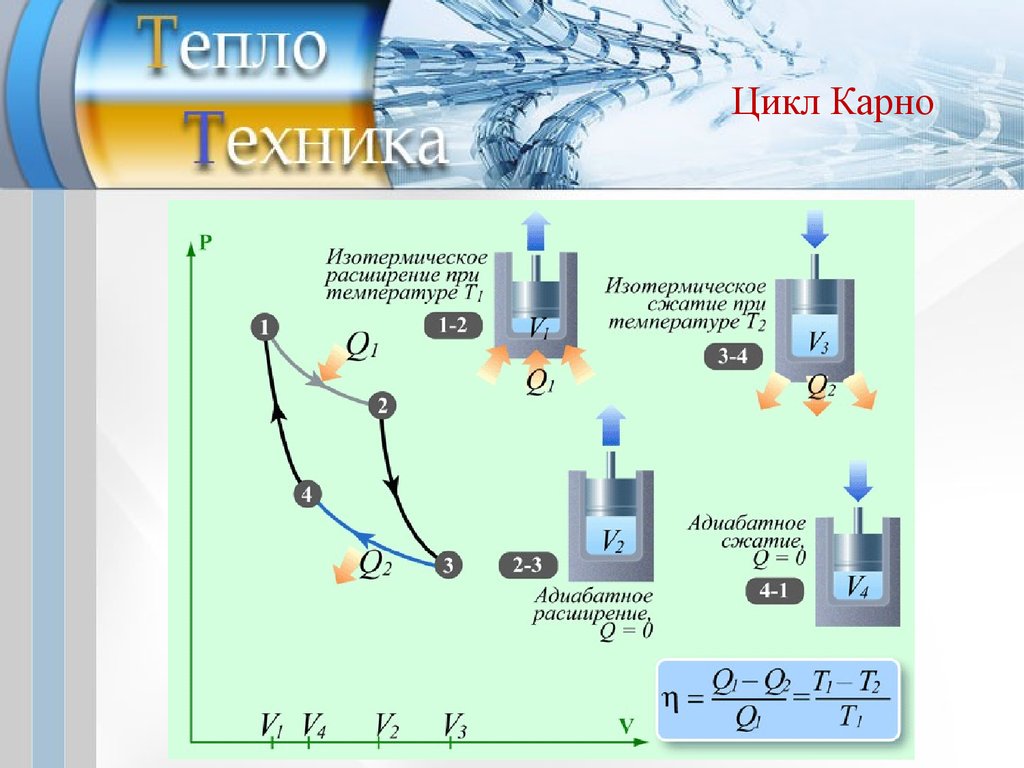
Цикл Карно состоит из 4-х процессов:
2-х изотермических и 2-х адибатных процессов.
15.
Цикл Карно16.
Цикл КарноТермический к.п.д. цикла Карно
Изотермический процесс 1-2:
Адиабатный процесс 2-3:
Изотермический процесс 3-4:
Адиабатный процесс 4-1:
Работа цикла:
u2
l1 = q1 = RT1 ln( ),
u1
l2 =
R(T1 - T2 )
,
k -1
u3
l3 = q2 = - RT2 ln( ),
u4
R (T1 - T2 )
l4 = ,
k -1
ln = l1 + l2 + l3 + l4 .
17.
Цикл КарноК.п.д. цикла:
Работа цикла:
u3
u2
RT1 ln( ) - RT2 ln( )
u3
u2
u1
u4
ln = RT1 ln( ) - RT2 ln( ), ht =
,
u2
u1
u4
RT1 ln( )
u1
k -1
k -1
u 2 u3
T
u
=
T
u
1 2
2 3 ,
Для адиабатного процесса 2-3
= .
или
k -1
k -1
u1 u4
и 4-1 выполняются равенства: T1u1 = T2u4 ,
ht =
Q1 - Q2 T1 - T2
=
.
Q1
T1
Теорема Карно. Величина термического к.п.д. цикла Карно
зависит лишь от величины отношения абсолютных температур и
не зависит от свойств рабочего тела.
18.
Приведенная теплотаТермический к.п.д. для цикла Карно
ht = 1 - q2 q1 = 1 - T2 T1 ,
следовательно
q2 q1 = T2 Tили
q 1T
1
1
=
q 2T
2
Изменим знак у теплоты
q2 ® - q2 ,
Тогда для цикла Карно
выполняется соотношение:
qi
åi T = 0.
.
19.
Приведенная теплотаВо всяком обратимом цикле Карно алгебраическая сумма
отношений количества сообщенного тепла к абсолютной
температуре, при которой оно сообщается, и количества
отведенного тепла к абсолютной температуре, при которой
оно отводится, равна 0.
Отношения q1/T1 и q2/T2 или в общем виде q/Т называются
приведенной теплотой.
20.
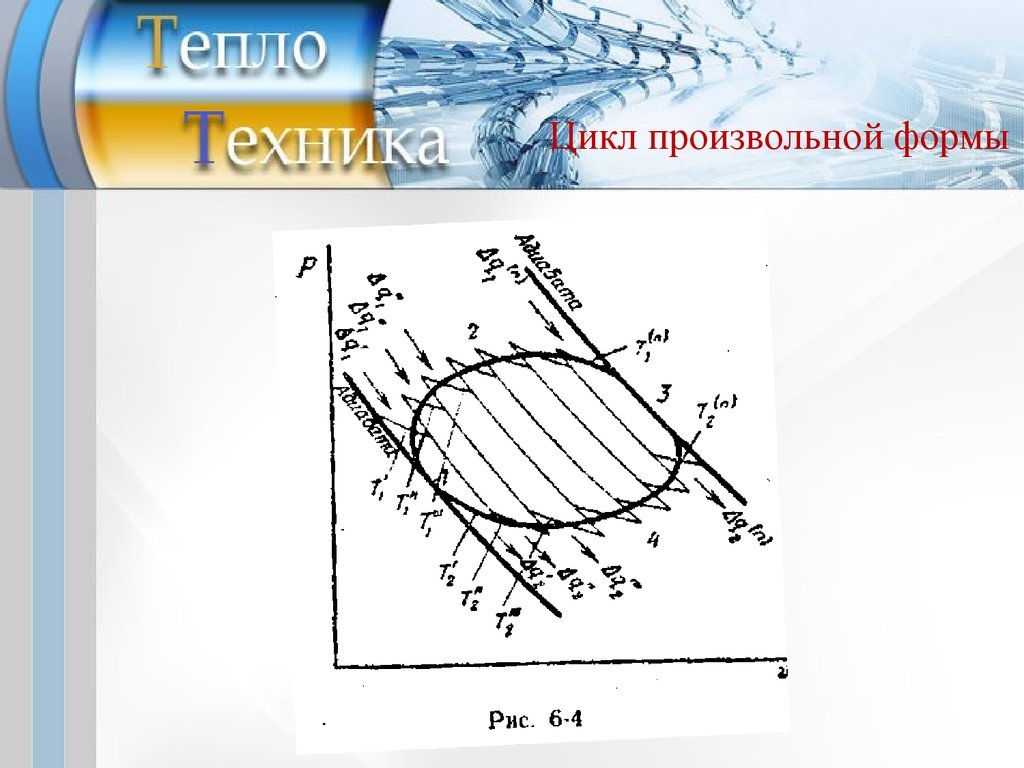
Цикл произвольной формы21.
Цикл произвольной формыn
Dq1( i )
Dq 2( i )
å1 T ( i ) + å1 T ( i ) = 0
1
2
n
Dq
или å
= 0.
1 T
n
По мере увеличения числа адиабат и изотерм
зигзагообразный контур составленного цикла будет по
своему очертанию все более приближаться к контуру
рассматриваемого произвольного цикла.
22.
Энтропиядля обратимого процесса
Для любого обратимого цикла интегральная сумма
приведенных теплот равна нулю.
dq
Ñ
ò T = 0.
Полное изменение энтропии в круговом обратимом т/д
процессе равно нулю.
Ñ
ò ds = 0.
Уравнение второго закона термодинамики для обратимых
процессов.
dq = T ds.
23.
Энтропия длянеобратимого процесса
Рассмотрим два последовательных круговых процесса:
необратимый и обратимый с одними и теми же тепловыми
резервуарами R1 и R2 . Их можно объединить в один
общий круговой процесс. В этом процессе сложная
система:
получила от резервуара R1 тепло Q1 + Q1¢,
получила от резервуара R2 тепло Q2 + Q2¢ ,
совершила работу
A = Q1 + Q1¢ + Q2 + Q2¢ .
Подберем тепло Q1¢ так, чтобы Q1¢ = -Q1 .
24.
Энтропия длянеобратимого процесса
Для обратимого процесса выполняется соотношение:
Q2¢ = T2
Q1
.
T1
В результате кругового процесса состояние резервуара R1
не изменится. Тепловой резервуар
отдаст
R2
тепло
Q1
Q1 Q2
¢
Q2 + Q2 = Q2 + T2
= T2 ( + ).
T1
T1 T2
За счет этого тепла будет произведена эквивалентная
работа
A = Q2 + Q2¢ .
25.
Неравенство КлаузиусаЕсли бы эта работа была положительна, то получился бы
процесс Томсона-Планка, что невозможно. Поэтому
должно быть A £ 0 или выполняться соотношение:
Q1 Q2
Tили
+ )£0
2(
T1 T2
Q1 Q2
( + ) £ 0.
T1 T2
В общем случае имеем неравенство Клаузиуса:
dQ
Ñ
ò T £ 0.
26.
Закон неубывания энтропииa
б
Пусть процессы 1а2- необратимый, 2б1-обратимый,
тогда из неравенства Клаузиуса следует:
dQ
dQ
dQ
Ñ
ò T º 1òа 2 T +1бò2 T £ 0.
27.
Законнеубывания энтропии
Так как 2б1-обратимый процесс, то
dQ
ò1б 2 T = S1 - S2
и неравенство Клаузиуса принимает вид:
dQ
S 2 - S1 ³ ò
.
T
1а 2
Если система адиабатически изолирована, то
S 2 ³ S1 .
dQ = 0
28.
Второе началотермодинамики
29.
Второе началотермодинамики
30.
Второе началотермодинамики
31.
Второе началотермодинамики




























 Физика
Физика








