Похожие презентации:
Второе начало термодинамики. Циклы. (Лекция 10)
1.
Лекция 102. §§ Циклы
Круговым процессом (циклом)называется процесс, при котором
система, пройдя ряд состояний,
возвращается в начальное состояние
A > 0 – прямой цикл
Работа совершается
системой за счет
подводимого тепла Q
(тепловой двигатель)
02
3.
A < 0 – обратныйцикл
Работа совершается
над системой
(холодильная машина)
Происходит превращение работы в
теплоту, т.к. выходит энергии больше,
чем входит.
A = ∫ pdV =
ò
pdV +
ò
pdV
L1
L2
(L)
(в каждой точке цикла выполняется УС)
03
4. §§ КПД цикла
Тепловая машинатермодинамически действующее
устройство, совершающее работу
за счет подводимого из вне тепла
Элементы тепловой машины
1) нагреватель
тела с очень
большой
2) рабочее тело
теплоемкостью
3) холодильник
04
5.
Для кругового процессаDU = 0
DQ = ∫ d Q =
dU
+
∫
pdV
=
∫
pdV
=
A
∫
т.е. работа совершается за счет
поступающей энергии
На участке цикла рабочее тело может
получать энергию: d Q1
= dU + pdV > 0
и отдавать: d Q2
= dU + pdV < 0
05
6.
ПустьQ1 – количество энергии, полученное
Q2
системой от нагревателя
– количество энергии, отданное
холодильнику
Тогда эффективность машины (КПД):
A
Q1 + Q2
h = = A = Q = Q1 + Q2 =
Q1
Q1
Q1 > 0
Q2
| Q2 |
=
= 1+
= 1Q2 < 0
Q1
Q1
06
7.
Существует бесконечное множествоциклов и у каждого свой КПД.
В механике циклы используют для
преобразования энергии (превращения
теплоты в работу).
На практике используется всего
несколько десятков циклов.
07
8. §§ Цикл Карно
Рассмотрим наиболее эффективный цикл,состоящий из двух изотерм T1 и T2 и
двух адиабат
Вычислим работу
тела за цикл:
A = A12 + A23
+ A34 + A41
08
9.
1→2 – изотермическое расширениеd A > 0 – за счет
нагревателя
d Q > 0, DU = 0
V2
A12 = n RT1 ln
V1
2→3 – адиабатическое расширение
d Q = 0, DU < 0
d A > 0 – за счет DU
A23 = -DU = -n CV (T2 - T1 )
09
10.
АналогичноV4
A34 = n RT2 ln
V3
A41 = -DU = -n CV (T1 - T2 )
TV
g -1
g -1
ìï T1V2
g -1
= T2V3
= const Þ í
g -1
g -1
ïî T1V1 = T2V4
следовательно
V2 V3
=
V1 V4
10
11.
Работа за циклA = A12 + A23 + A34 + A41 = A12 + A34
Вычислим КПД:
V2
n R (T1 - T2 ) ln
V1
A
T2
h= =
= 1Q1
V2
T1
n RT1 ln
V1
11
12.
Теорема Карно–КлаузиусаКПД тепловой машины, работающей
по циклу Карно, зависит только
от температур T1 и T2 нагревателя
и холодильника, но не зависит
от устройства машины и вида
рабочего тела
Теорема Карно (2)
КПД всякой ТМ не может превосходить
КПД идеальной ТМ, работающей по
циклу Карно, с теми же самыми
температурами нагревателя и
холодильника
12
13. §§ Обратимые процессы
Обратимым называется процесс,для которого возможен обратный
переход из конечного состояния
в начальное через те же
промежуточные состояния,
что и в прямом процессе
или если систему можно вернуть в
исходное состояние хотя бы одним
способом и притом так, чтобы состояние
тел вне системы осталось неизменным.
13
14.
Процесс – равновесный, если системапроходит ряд непрерывно следующих
друг за другом равновесных состояний
Условия равновесности:
1) непрерывность всех величин,
характеризующих процесс
2) бесконечно малая скорость
изменений в системе
Необходимое и достаточное условие
обратимости – равновесность.
14
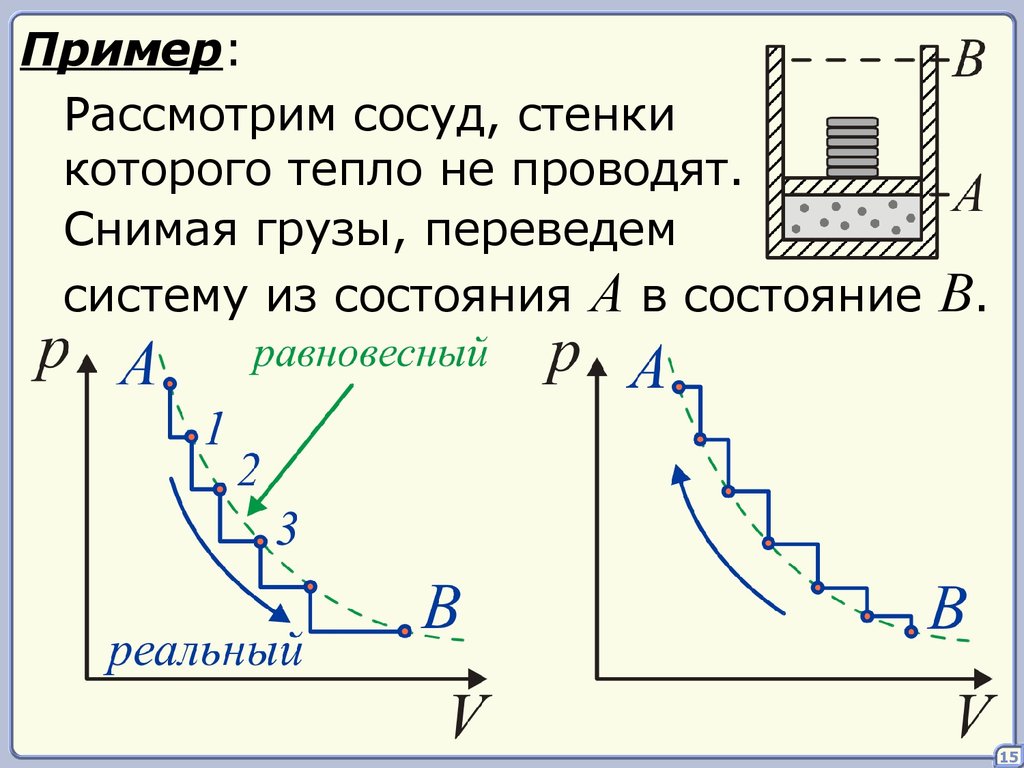
15.
Пример:Рассмотрим сосуд, стенки
которого тепло не проводят.
Снимая грузы, переведем
систему из состояния A в состояние
B.
15
16.
Все реальные процессы протекают сконечной скоростью и являются
необратимыми и неравновесными.
При любом возмущении в системе
требуется время для установления
равновесия.
Это приводит к тому, что в обратном
процессе газ совершит большую
работу, чем в прямом.
16
17. §§ Неравенство Клаузиуса
Сравним КПД неравновесной иравновесной машины, работающей
по циклу Карно:
Q2
Q1 Q2
T2
1+
Þ
+
£0
£ 1Q1
T1 T2
T1
приведенная теплота
dQ
∫ T £0
– неравенство Клаузиуса
17
18. §§ Энтропия идеального газа
I-е начало в дифференциальной формеd Q = dU + pdV = n CV dT + pdV
функция состояния
полный дифференциал
бесконечно малое приращение
(Q – не функция состояния, как и
T левую и правую части:
dQ
dT p
= n CV
+ dV
T
T T
A)
Разделим на
18
19.
Из уравнения М–К:p nR
pV = n RT Þ =
T V
Получаем
dQ
dT
dV
= n CV
+n R
T
T
V
dQ
= n CV d ln T +n R d ln V
T
dQ
= n d [ CV ln T + R ln V ]
T
19
20.
Левая часть – полный дифференциал,тогда правая часть – дифференциал
новой функции состояния
dQ
= dS
T
S – энтропия
Это выражение справедливо только для
равновесных (обратимых) процессов.
Оно позволяет вычислить разность
но не абсолютное значение.
S,
20
21. §§ Основное уравнение ТД
Согласно первому началуd Q = dU + pdV
и для равновесного процесса получаем
dU + d A
dS =
T
основное
уравнение
термодинамики
Оно справедливо при химических
реакциях и при фазовых переходах.
В физике имеет множество следствий.
21
22. §§ Физический смысл S
Рассмотрим идеальный газ,ν = 1 моль, в объеме V.
Разделим весь объем
ячейками размером á l ñ
á l ñ – средняя длина свободного пробега
V = N [ ál ñ ]
3
N – число ячеек
NA – число занятых ячеек
(NA << N)
22
23.
Вычислим Г – число микросостояний,которое может реализоваться в системе
Оно равно числу способов размещения
NA молекул по N ячейкам:
N!
G=
( N - N A )!
Формула Стирлинга:
N
e ö
æNö æ
G=ç ÷ ç
÷
è e ø è N - NA ø
Nö
æ
N! ≈ ç ÷
eø
è
N -N
N
A
23
24.
NAN -N A
æ N ö
æNö
≈ ç ÷
ç
÷
èeø
è N - NA ø
G2
N2
V2
ln
= N A ln
= N A ln
G1
N1
V1
æNö
=ç ÷
èeø
NA
Для идеального газа
dS = n d [ CV ln T + R ln V ]
тогда для n = 1 моль и T = const :
V2
DS = R ln
V1
24
25.
T = constDS = S 2 - S1 = k B ln G 2 - k B ln G1
Следовательно, при
и
S = k B ln G + const
const часто полагают равной нулю
и
считают, что энтропия пропорциональна
логарифму числа пространственных
микросостояний
S = k B ln G
Энтропия является мерой беспорядка
(разупорядочения) в системе.
25
26. §§ II-е начало термодинамики
Система, предоставленная самой себе,приходит к равновесному состоянию,
т.е. энтропия не уменьшается в
предоставленной самой себе системе.
I-е начало говорит о соотношении между
величинами, характеризующими систему
II-е начало указывает направление
изменений в системе, если они должны
произойти.
26
27.
Пусть замкнутая система переходит изсостояния 1 в состояние 2.
Возвратим систему в
состояние 1 с помощью
обратимого процесса
∫
dQ
dQ
dQ
=ò
+ò
£0
T L T L T
1
=0
т.к. система
изолирована
2
S1 - S2
S1 £ S 2
27
28.
Следовательно,При переходе замкнутой системы
из состояния 1 (с S1) в 2 (с S2),
энтропия либо увеличивается,
либо не изменяется
Замечание: о «тепловой смерти»
Клаузиус, рассматривая Вселенную
как замкнутую систему, утверждал:
«энтропия Вселенной стремится
к максимуму»
28
29. §§ Тепловая теорема Нернста
Первое утверждениеПри приближении к абсолютному нулю
энтропия стремится к определенному
конечному пределу
T
S - S0 =
ò
T0
dQ
T
– т.е. этот интеграл сходится.
29
30.
Второе утверждениеВсе процессы при абсолютном нуле
температур, переводящие систему
из одного равновесного состояния
в другое, происходят без изменения
энтропии
Классическое описание системы при
абсолютном нуле неприменимо, т.к.
оно допускает бесконечное множество
состояний.
Необходимо рассмотрение с квантовых
позиций.
30

















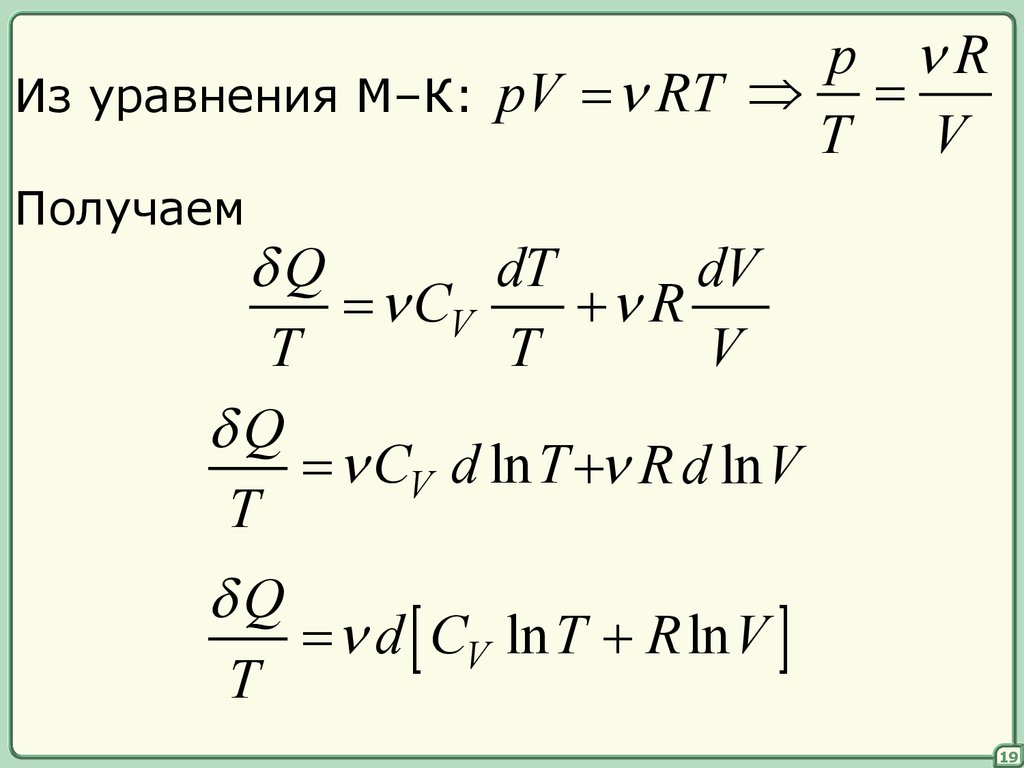











 Физика
Физика








