Похожие презентации:
Теплотехника. Второе начало термодинамики. (Лекция 5)
1.
Второе началотермодинамики
За нуль энтальпии и энтропии воды принимаются энтальпия
и энтропия воды при 0 °С, а поэтому i0 = 0 и S0 = 0.
Изменение энтропии воды при нагреве ее от 0 °С (273 К) до
температуры кипения Ts определяется:
Ts
Ts
Ts
dq
b dT
b
S¢ = ò
= ò cp
= c p ln
.
T 273 T
273
273
2.
Процессиспарения воды
При испарении жидкость, нагретая до температуры кипения
Ts, обращается при постоянной температуре и давлении в
пар, т. е. процесс испарения - изобарно-изотермический и
в диаграмме Т - S он изображается горизонтальной линией
b' - с'.
Теплота, на превращение 1 кг жидкости при температуре
кипения в сухой насыщенный пар, называется теплотой парообразования r (площадь S'b'c'S"S' ).
Теплота r - обратная функция p и обращается в 0 при pкр.
При низких p теплота r значительно больше теплоты
жидкости. При увеличении давления разность между ними
уменьшается и при давлении р = 90 бар q' r.
3.
Второе началотермодинамики
Изменение энтропии при испарении равно:
S '' S' = r/TS .
При критическом давлении r = 0 и S" = S'.
Теплота сухого насыщенного пара.
Состояние сухого насыщенного пара (х=1) определяется
лишь одним параметром состояния - ps или ts. Температура
сухого насыщенного пара, равная температуре кипения
(насыщения), может быть при ps 20 бар приближенно
оценена по формуле ts 100 рs [°С], а плотность " 0,5ps
[кг/м3].
4.
Второе началотермодинамики
Полной теплотой сухого насыщенного пара " называется
теплота, расходуемая при ps = const на получение 1 кг
сухого насыщенного пара из воды при 0 °С:
¢¢ = q¢ + r.
Если пренебречь сжимаемостью воды, то
¢¢ = i¢¢,
т. е. полная теплота сухого насыщенного пара приближенно
равна его энтальпии.
Энтропия сухого насыщенного пара S" равна
Ts
r
r
b
S ¢¢ = S ¢ + = c p ln
+ .
T
273 Ts
5.
Теплота влажного параТеплота влажного пара х , расходуемая на нагревание 1 кг
воды от 0 °С до кипения и неполное (в количестве х) ее
испарение:
¢
x = q + rx = ix .
Состояние влажного пара определяется 2-мя параметрами:
давлением (температурой ts) насыщения ps и степенью
сухости х. Удельный объем влажного пара как объем смеси,
состоящей из (1-х) долей воды и х долей пара, равен:
vx = (1 x)v¢ + xv¢¢.
Энтропия влажного пара определяется:
S x = c ln
b
p
Ts
273
r
+
.
Ts x
6.
Процесс перегрева параТеплота, сообщаемая пару в процессе его перегрева при p =
const, (площадь S"c'd'SS") равна:
t
p
n
¢¢
q = i i = ò cn dt = c pm (t t s ),
ts
где i - энтальпия перегретого пара; сnрm - средняя
теплоемкость пара в интервале температур t и ts.
7.
Процесс перегрева параТеплота перегретого пара количество теплоты, которое
необходимо подвести к 1 кг воды при 0 °С, чтобы получить
из нее перегретый пар температурой t:
= q¢ + r + c (t t s ).
n
pm
Изменение энтропии в процессе перегрева может найдено из
2-го закона термодинамики:
T
T
dq
T
n dT
n
S S ¢¢ = ò
= ò cp
= c pm ln .
T TS
T
TS
TS
откуда энтропия перегретого пара S
TS
r
T
n
S = c ln
+ + c pm ln .
273 TS
TS
n
p
8.
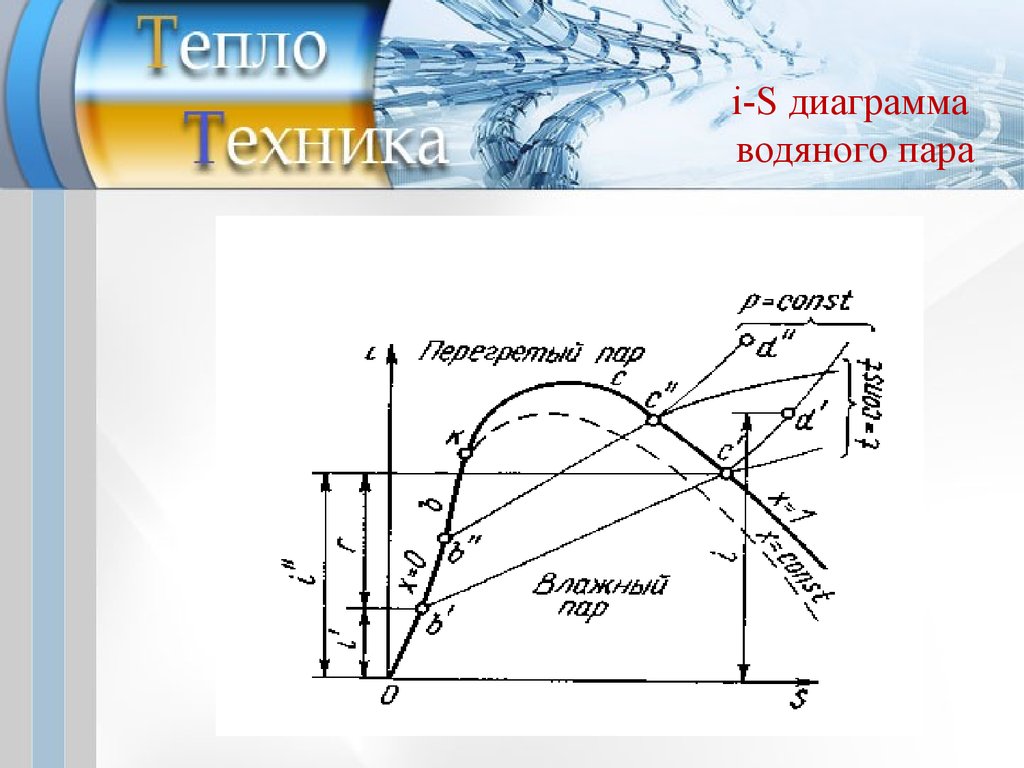
i-S диаграммаводяного пара
9.
i-S диаграммаводяного пара
Точка 0 - энтальпия воды при 0 °С; линия b (x = 0) - кривая
кипения; точка k - критическая точка; линия с (х=1) кривая конденсации (отделяет область влажного пара от
области перегретого пара).
Изобары воды почти совпадают с кривой кипения, в
области влажного пара изобары - веерообразно
расходящиеся пучки прямых линий, касательных к кривой
конденсации, а в области перегретого пара - кривые с
выпуклостьюв сторону оси S.
Линии ob'c'd' и ob"c"d" - изобары парообразования.
10.
Влажный воздухСмесь сухого воздуха с водяным паром называется
влажным воздухом.
Насыщенный влажный воздух – смесь сухого воздуха с
насыщенным водяным паром.
Ненасыщенный влажный воздух – смесь сухого воздуха с
ненасыщенным водяным паром.
Температура, до которой нужно охладить ненасыщенный
влажный воздух, чтобы он стал насыщенным, называется
температурой точки росы.
11.
Влажный воздухРасчет процессов с влажным воздухом проводится при
условии, что количество сухого воздуха не меняется:
M в = const = 1кг.
Давление влажного воздуха - есть сумма парциальных
давлений воздуха и водяного пара:
p = pрв +.
п
Абсолютная влажность воздуха – это масса пара,
содержащегося в 1м3 влажного воздуха.
Мп Мп
п =
=
.
Vп Vсм
12.
Влажный воздухОтносительная влажность воздуха – отношение
абсолютной влажности ненасыщенного воздуха к
максимально возможной абсолютной влажности воздуха
при той же температуре:
п
pп
j=
=
.
max p max
Влагосодержание – это отношение массы пара,
содержащегося во влажном воздухе, к массе сухого
воздуха.
M п п é кг ù é г ù
d=
=
, ê ú , ê ú.
Mкг
в кгë û ë û
в
13.
Влажный воздухВыведем формулу связи между влагосодержанием и
парциальным давлением:
pвV = M в RвT , Rв = R 0.029,
pпV = M п RпT , Rп = R 0.018.
Разделив почленно первое уравнение на второе, получим:
pв 0.622
=
.
pп
d
Учитывая, что pв = p pп находим:
pп
d = 0.622
.
p pп
14.
Влажный воздухВыражение относительной влажности воздуха через
влагосодержание:
d
p
j=
×
.
0.622 + d pmax
Относительная влажность воздуха и влагосодержание
могут быть определены с помощью психрометра,
состоящего из двух термометров – сухого и мокрого или
по i-d диаграмме влажного воздуха.
15.
Теплоемкостьвлажного воздуха
Изобарную теплоемкость обычно относят к 1 кг сухого
воздуха, она равна сумме теплоемкостей 1 кг сухого
воздуха и d кг пара:
c p = c pв + c pп d .
Можно принять удельные изобарные теплоемкости сухого
воздуха и водяного пара равными:
cкДж
pв 1 кг К(
×const
)=
cкДж
кг К
pп = 1 ,96
(const
× )=
Тогда
c p = 1 + 1,96 d .
,
.
16.
Энтальпиявлажного воздуха
Энтальпия влажного воздуха определяется как энтальпия
газовой смеси, состоящей из 1кг сухого воздуха и d кг
водяного пара:
I = iв + iп d ,
где iв = c pв t t -энтальпия сухого воздуха,
iп = c pвод t н + r + c pп (t t н ) -энтальпия водяного пара,
находящегося во влажном воздухе в перегретом состоянии,
t - температура влажного воздуха,
r - скрытая теплота парообразования,
cкДж
(кг× ) - удельная изобарная
pвод = 4,19 К
теплоемкость воды,
17.
Формула Рамзинаt н - температура насыщения при парциальном давлении
пара в смеси.
0
Учитывая, что для интервала температур 0 £ tС
£
100
н
r 2500 2,3tкДж
кг К× ,
н
iп = 4,19 t н + 2500 2,3t н + 1,96(t t н ) = 2500 + 1,96 t,
получим известную формулу Рамзина для энтальпии
влажного воздуха:
I = t + (2500 + 1,96 t) d.
18.
Диаграмма РамзинаId-диаграмма влажного воздуха предложена проф.
Л.К.Рамзиным в 1918г.
В этой диаграмме по оси абсцисс
откладывается влагосодержание
воздуха d,, а по оси ординат ,
расположенной под углом 135° – его
энтальпия I. Диаграмма строится для
давления воздуха р=745 мм рт. ст., но с
достаточной точностью ее можно
применять и при небольших отклонениях
от него.
19.
Диаграмма РамзинаКроме того, на диаграмме имеются линии постоянных
температур влажного воздуха (прямые линии), кривые
относительной влажности воздуха, кривая парциальных
давлений
По id-диаграмме, зная температуру t и
относительную влажность j можно
определить энтальпию i,
влагосодержание d и парциальное
давление pп . По температурам
сухого и мокрого термометра можно
определить температуру точки росы.
20.
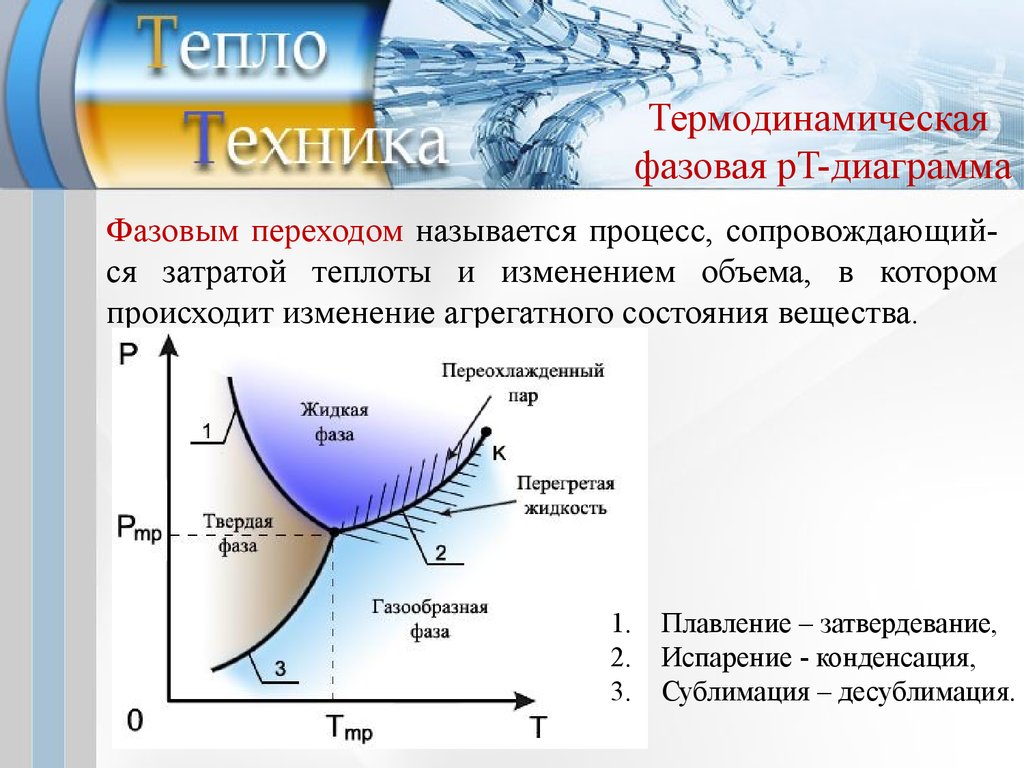
Термодинамическаяфазовая pT-диаграмма
Фазовым переходом называется процесс, сопровождающийся затратой теплоты и изменением объема, в котором
происходит изменение агрегатного состояния вещества.
1.
2.
3.
Плавление – затвердевание,
Испарение - конденсация,
Сублимация – десублимация.
21.
Термодинамическаяфазовая pT-диаграмма
Процессы фазовых превращений из одного состояния в
другое происходят при постоянной температуре с
поглощением (выделением) определенного количества
теплоты:
1.Температура (теплота) плавления (затвердевания),
2.Температура (теплота) кипения (конденсации),
3.Температура (теплота) сублимации (десублимации).
Тройная точка – точка термодинамического равновесия
трех различных фаз вещества: твердой, жидкой и
газообразной, т.е. пропадает различие между этими
тремя фазами.
22.
УравнениеКлайперона-Клаузиуса
Уравнение Клайперона-Клаузиуса описывает связь между
термическими величинами (температура, давление,
удельный объем и калорической величиной (теплота
фазового перехода).
dp
q = T (v¢¢ v¢)
,
dT
dp
q
=
= tg a .
dT T (v¢¢ v¢)
Для всех нормальных жидкостей:
v¢¢ v¢ > 0, tg a > 0, a < p 2.
Для аномальной жидкости (вода):
v¢¢ v¢ < 0, tg a < 0, a < p 2.
23.
УравнениеКлайперона-Клаузиуса
24.
УравнениеКлайперона-Клаузиуса
Уравнение Клайперона-Клаузиуса описывает связь между
термическими величинами (температура, давление,
удельный объем и калорической величиной (теплота
фазового перехода).
dp
q = T (v¢¢ v¢)
,
dT
dp
q
=
= tg a .
dT T (v¢¢ v¢)
Для всех нормальных жидкостей:
v¢¢ v¢ > 0, tg a > 0, a < p 2.
Для аномальной жидкости (вода):
v¢¢ v¢ < 0, tg a < 0, a < p 2.






















 Физика
Физика








