Похожие презентации:
Особенности вычислений с исключением ошибок округлений. Лекция 9
1.
Контрольная работапо курсу
«Машинная арифметика в рациональных числах»
Москва, 2020
2.
ОСОБЕННОСТИ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОКОКРУГЛЕНИЙ
1. Необходимость вычислений с очень «длинными
числами», что является их серьёзным недостатком
Например
A1/B1 + A2/B2 = (A1B2+A2B1)/(B1B2)
2. Если псевдопереполнение возникают в процессе
вычислений, но не в конечном результате, то он будет
правильным. Например, для дробей Фарея 3-го порядка
(1/2)*(1/2) + (3/2)*(1/2) = 1
10*10+11*10=100+110 = 210 mod 19 = 1
2
3.
ГДЕ ПРИМЕНЯТЬ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОКОКРУГЛЕНИЙ?
1. Для любых вычислительных задач о которых известно,
что решения это дроби Фарея определенного порядка или
есть оценка сверху для них.
2) Для задач, где требуется очень высокая точность
вычислений.
3
4.
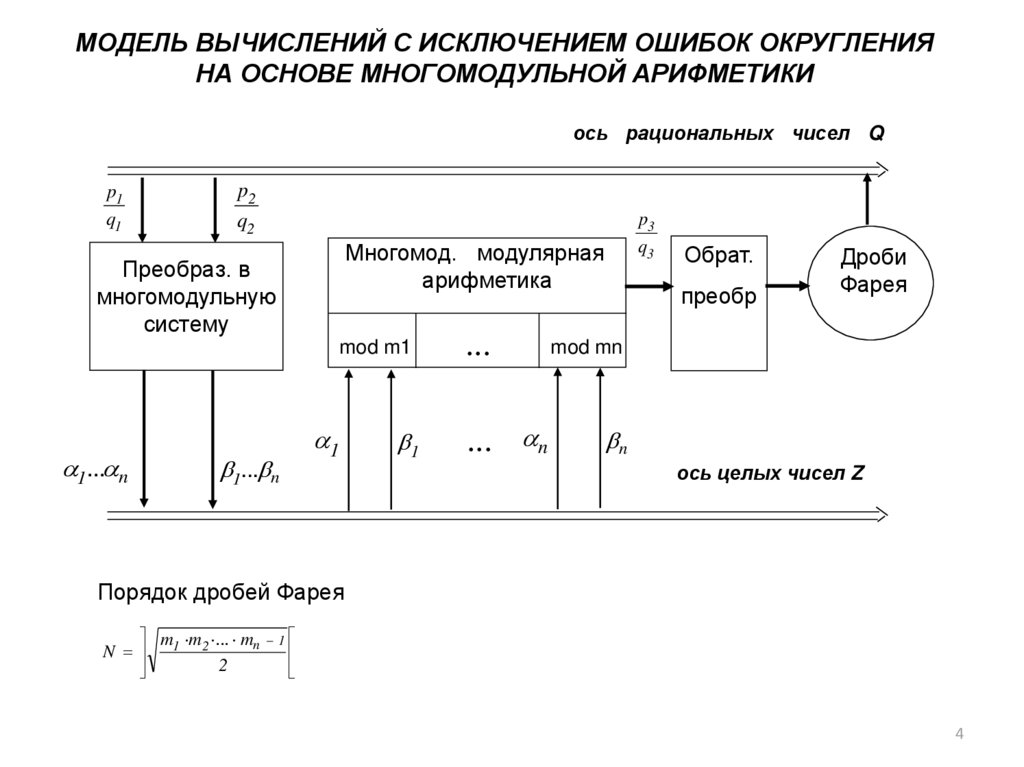
МОДЕЛЬ ВЫЧИСЛЕНИЙ С ИСКЛЮЧЕНИЕМ ОШИБОК ОКРУГЛЕНИЯНА ОСНОВЕ МНОГОМОДУЛЬНОЙ АРИФМЕТИКИ
ось рациональных чисел Q
p1
q1
p2
q2
Многомод. модулярная
арифметика
Преобраз. в
многомодульную
систему
mod m1
1... n
p3
q3
1
1... n
1
...
...
Обрат.
преобр
Дроби
Фарея
mod mn
n
n
ось целых чисел Z
Порядок дробей Фарея
m m ... mn
N 1 2
2
1
4
5.
Примере для схемы вычислений с исключениемошибок округления по нескольким модулям
(A-d0)*(m1 ^-1) = d1 + m2 *d2
(A-d0)*(m1 ^-1) - d1=m2 *d2
(?, 3, 4) – 3 = (?,0,1)
m2 ^(-1) mod m3 = 3
(?,?,3)
d2=(?,0,1)*(?,?,3) = 3
5
6.
Оценки сверху для задач(A-d0)*(m1 ^-1) = d1 + m2 *d2
(A-d0)*(m1 ^-1) - d1=m2 *d2
(?, 3, 4) – 3 = (?,0,1)
m2 ^(-1) mod m3 = 3
(?,?,3)
d2=(?,0,1)*(?,?,3) = 3
6
7.
Параллельная реализация вычислений сисключением ошибок округления
(A-d0)*(m1 ^-1) = d1 + m2 *d2
(A-d0)*(m1 ^-1) - d1=m2 *d2
(?, 3, 4) – 3 = (?,0,1)
m2 ^(-1) mod m3 = 3
(?,?,3)
d2=(?,0,1)*(?,?,3) = 3
7
8.
Избыточная система счисления8
9.
Избыточная система счисления9
10.
Избыточная система счисления10
11.
Избыточная система счисления11
12.
Избыточная система счисления12
13.
Избыточная система счисления13
14.
Возможная реализация схемы высокоточных вычислений сотложенным округлением с использованием многоядерного
процессора
Рациональные числа
A
B
Традиционные
вычисления
C
A
B
A
B
A
…
A P1
ЯДРО 1
AР
В P2
В P1
С P1
N 1
BР
С P1
Целые числа
ЯДРО N-1
ЯДРО 2
A P2
B
N 1
С P2
С P2
CР
CР
N 1
…
ЯДРО N
C
14
N 1
15.
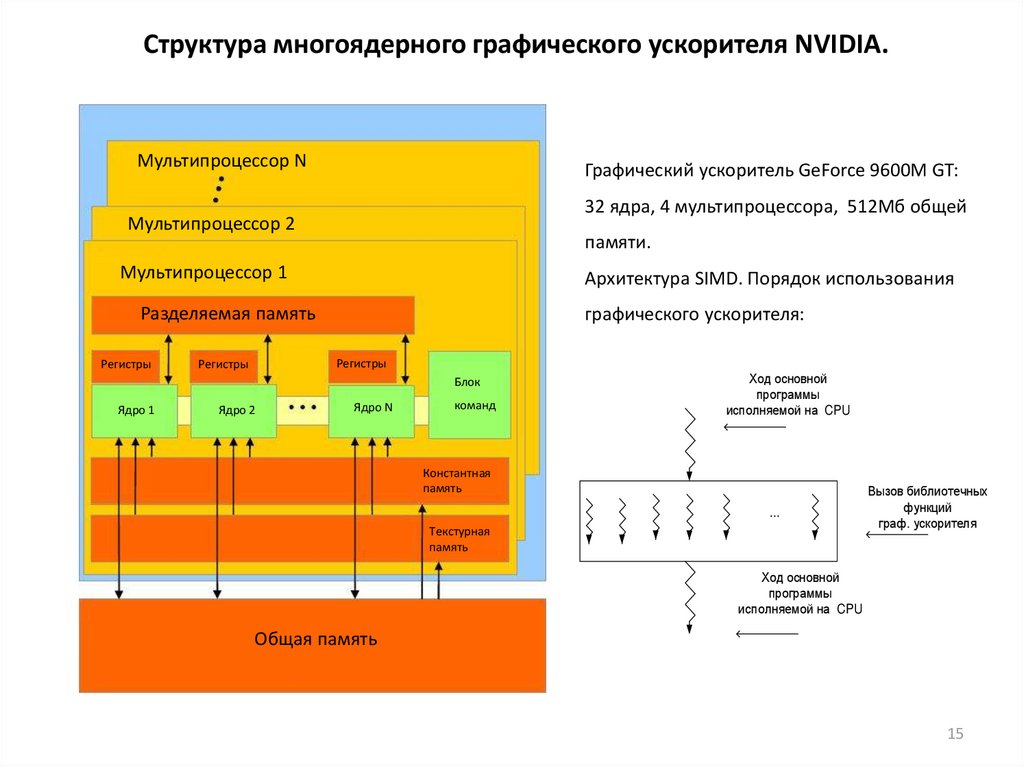
Структура многоядерного графического ускорителя NVIDIA.Мультипроцессор N
Графический ускоритель GeForce 9600M GT:
32 ядра, 4 мультипроцессора, 512Мб общей
Мультипроцессор 2
памяти.
Мультипроцессор 1
Архитектура SIMD. Порядок использования
Разделяемая память
Регистры
графического ускорителя:
Регистры
Регистры
Блок
Ядро 1
Ядро 2
Ядро N
команд
Ход основной
программы
исполняемой на CPU
Константная
память
...
Текстурная
память
Вызов библиотечных
функций
граф. ускорителя
Ход основной
программы
исполняемой на CPU
Общая память
15
16.
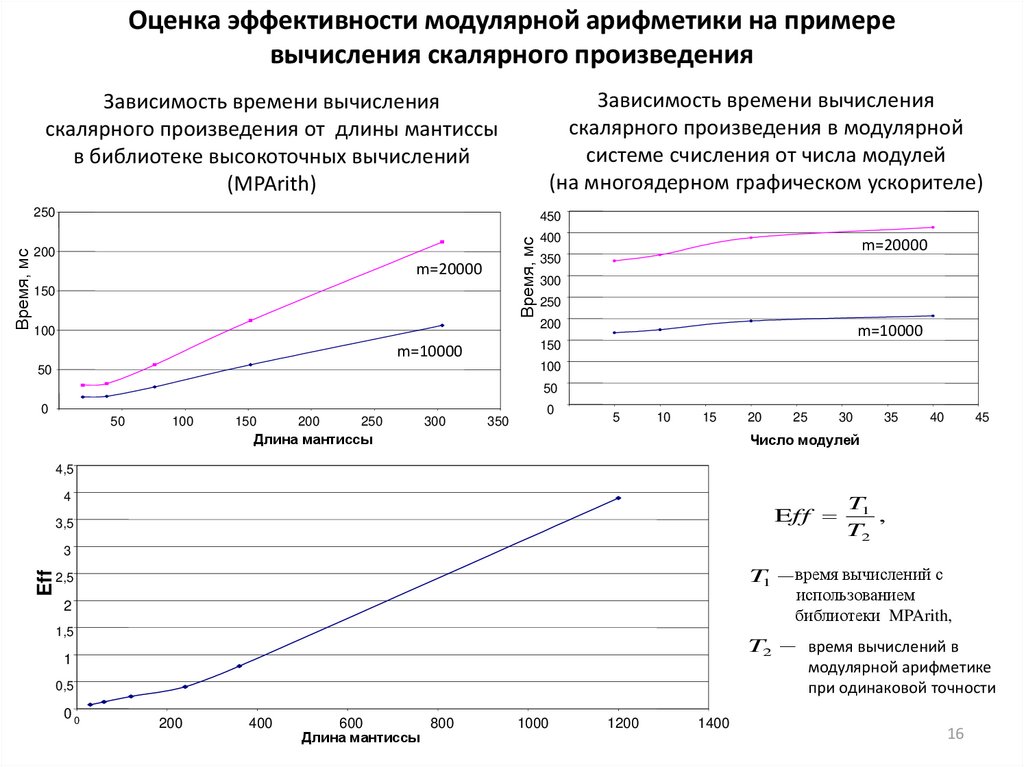
Оценка эффективности модулярной арифметики на примеревычисления скалярного произведения
Зависимость времени вычисления
скалярного произведения в модулярной
системе счисления от числа модулей
(на многоядерном графическом ускорителе)
Зависимость времени вычисления
скалярного произведения от длины мантиссы
в библиотеке высокоточных вычислений
(MPArith)
Время, мс
450
200
m=20000
150
400
m=20000
350
300
250
200
100
m=10000
150
m=10000
100
50
50
0
0
50
100
150
200
250
300
350
5
10
15
Длина мантиссы
20
25
30
35
40
45
Число модулей
4,5
4
Eff
3,5
T1
,
T2
3
Eff
Время, мс
250
T1 время вычислений с
2,5
использованием
библиотеки MPArith,
2
1,5
T2 время вычислений в
1
модулярной арифметике
при одинаковой точности
0,5
00
200
400
600
800
Длина мантиссы
1000
1200
1400
16
17.
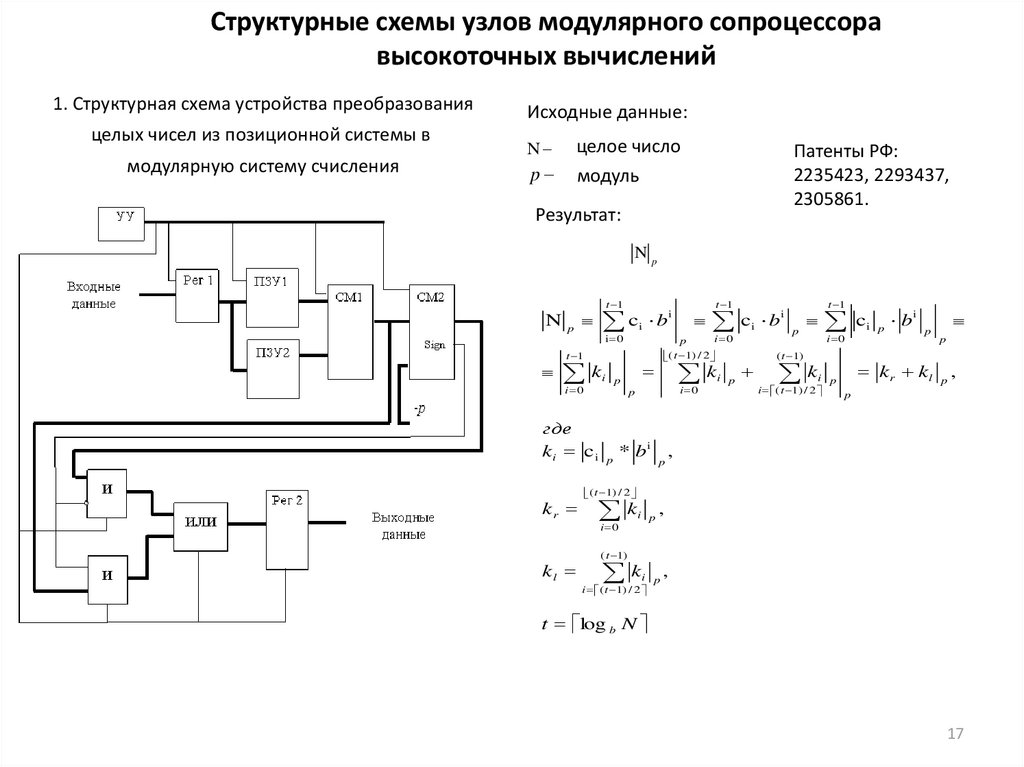
Структурные схемы узлов модулярного сопроцессоравысокоточных вычислений
1. Структурная схема устройства преобразования
целых чисел из позиционной системы в
модулярную систему счисления
Исходные данные:
N
целое число
модуль
p
Патенты РФ:
2235423, 2293437,
2305861.
Результат:
Np
N
p
t 1
c i bi
i 0
t 1
ki
kr
kl
i 0
p
где
ki c i
p
* bi
t 1
i 0
p
( t 1) / 2
p
i 0
p
ki
p
c i bi
p
t 1
i 0
( t 1)
k
i p
i ( t 1) / 2
p
ci
p
bi
p
k r kl
p
p
,
,
( t 1) / 2
k
i 0
i p
,
( t 1)
k
i p
i ( t 1) / 2
,
t log b N
17
18.
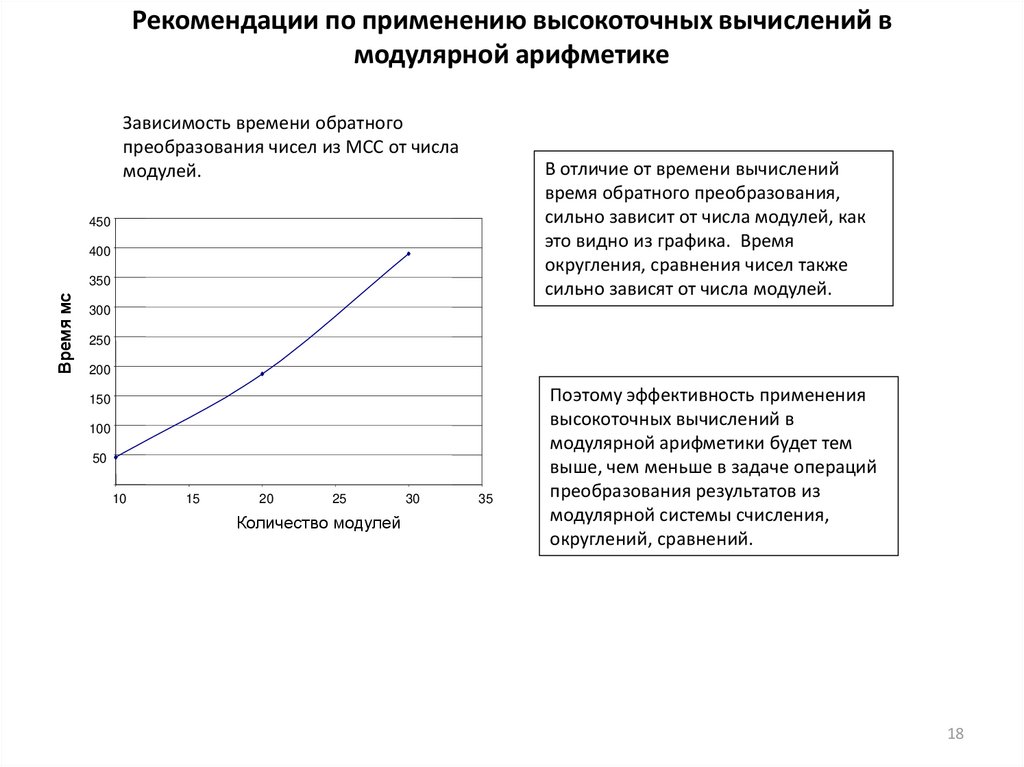
Рекомендации по применению высокоточных вычислений вмодулярной арифметике
Зависимость времени обратного
преобразования чисел из МСС от числа
модулей.
В отличие от времени вычислений
время обратного преобразования,
сильно зависит от числа модулей, как
это видно из графика. Время
округления, сравнения чисел также
сильно зависят от числа модулей.
450
400
Время мс
350
300
250
200
150
100
50
10
15
20
25
Количество модулей
30
35
Поэтому эффективность применения
высокоточных вычислений в
модулярной арифметики будет тем
выше, чем меньше в задаче операций
преобразования результатов из
модулярной системы счисления,
округлений, сравнений.
18













 Математика
Математика








