Моделирование сферы производства

1. ТЕМА 3. Моделирование сферы производства

3.1. Моделирование сферы производства:
основные понятия.
3.2. Производственные функции с
взаимозаменяемыми ресурсами.
3.3. Производственные функции с
взаимодополняемыми ресурсами и функции
производственных затрат.
3.4. Типовые производственные функции.

2. 3.1. Моделирование сферы производства: основные понятия

3. Цель моделирования

Цель моделирования сферы производства:
изучение взаимосвязи между затратами ресурсов и
выпуском продукции с целью выбора наиболее
эффективных вариантов использования ресурсов на
микро- и макроуровне.
Основной инструмент: производственные функции.
.

4. Производственная функция

Производственная функция
y = f(X), X = (x1, ..., xm)
Характеризует
зависимость
«затратывыпуск», то есть максимально возможный
объем выпуска продукта, который можно
получить при использовании разнообразных
ресурсов (факторов производства).

5. Основные характеристики системы: 3. Структура.

Основные характеристики системы:
Изокванты
3. Структура.
Изокванта - множество точек, удовлетворяющих
уравнению постоянного выпуска f(X) = q.
Свойства изоквант:
• они никогда не пересекаются друг с другом;
• большему выпуску продукции соответствует
более удаленная от начала координат
изокванта;
• если все ресурсы абсолютно необходимы для
производства, то изокванты не имеют общих
точек с осями координат.

6. Основные характеристики системы: 3. Структура.

Основные
характеристики
системы:
ПФ и основные
характеристики
технологии
3. Структура.
1. Средняя эффективность использования i-того ресурса:
f (X )
APi
xi

7. Основные характеристики системы: 3. Структура.

Основные
характеристики
системы:
ПФ и основные
характеристики
технологии
3. Структура.
2. Предельная
ресурса:
эффективность
использования
i-того
f ( X )
MPi
xi
Величина MPi ≥ 0 показывает прирост выпуска продукта
при увеличении затрат ресурса i на малую единицу.
2f ( X )
Если MPii x 2
< 0, это означает, что предельная
i
эффективность i-того ресурса падает.

8. Типы производственных функций

1. По количеству учитываемых факторов:
- однофакторная ПФ: y = f (x);
- многофакторная ПФ: y = f(x1,…, xm).
2. По характеру взаимосвязи факторов:
- производственные функции с взаимозаменяемыми
ресурсами;
- производственные функции с взаимодополняемыми
ресурсами.
3.По способу отражения фактора времени:
- статические;
- динамические.
4. По используемому математическому аппарату.

9. 3.2. Производственные функции с взаимозаменяемыми ресурсами

10. Основные характеристики системы: 3. Структура.

Основные
характеристики системы:
ПФ с взаимозаменяемыми
ресурсами:
общие свойства
3. Структура.
Взаимозаменяемость
ресурсов
в
производственной функции у = f(X) означает,
что один и тот же объем выпуска продукции
может
быть
получен
при
разных
комбинациях ресурсов.

11. Основные характеристики системы: 3. Структура.

Основные
характеристики
системы:
ПФ с взаимозаменяемыми
ресурсами:
основные характеристики
3. Структура.технологии
3. Эквивалентная замена ресурсов.
Условия эквивалентной взаимозаменяемости ресурсов в
точке Х°:
y MPi xi 0
i M
Для двух ресурсов:
y MPk xk MPl xl 0

12. Основные характеристики системы: 3. Структура.

Основные
характеристики
системы:
ПФ с взаимозаменяемыми
ресурсами:
основные характеристики
3. Структура.технологии
3. Эквивалентная замена ресурсов.
Предельная норма эквивалентной замены ресурсов k и l:
xk
MPl ( X 0 )
MRTS kl
0
0
xl
MPk ( X )
Изоклинали – кривые, отображающие комбинации
ресурсов, для которых предельные нормы эквивалентной
замены одинаковы.

13. Основные характеристики системы: 3. Структура.

Основные
характеристики
системы:
ПФ с взаимозаменяемыми
ресурсами:
основные характеристики
3. Структура.технологии
Изокванты и изоклинали производственной функции

14. Основные характеристики системы: 3. Структура.

Основные
характеристики
системы:
ПФ с взаимозаменяемыми
ресурсами:
основные характеристики
3. Структура.технологии
4. Эластичность выпуска.
Коэффициент эластичности выпуска от затрат ресурса i
показывает, на сколько процентов увеличится выпуск
продукта при увеличении затрат i-того ресурса на 1% и при
неизменных затратах других ресурсов:

15. Основные характеристики системы: 3. Структура.

Основные
характеристики
системы:
ПФ с взаимозаменяемыми
ресурсами:
основные характеристики
3. Структура.технологии
4. Эластичность выпуска.
или для некоторых интервалов изменения компонент
вектора X0:

16. Основные характеристики системы: 3. Структура.

Основные
характеристики
системы:
ПФ с взаимозаменяемыми
ресурсами:
основные характеристики
3. Структура.технологии
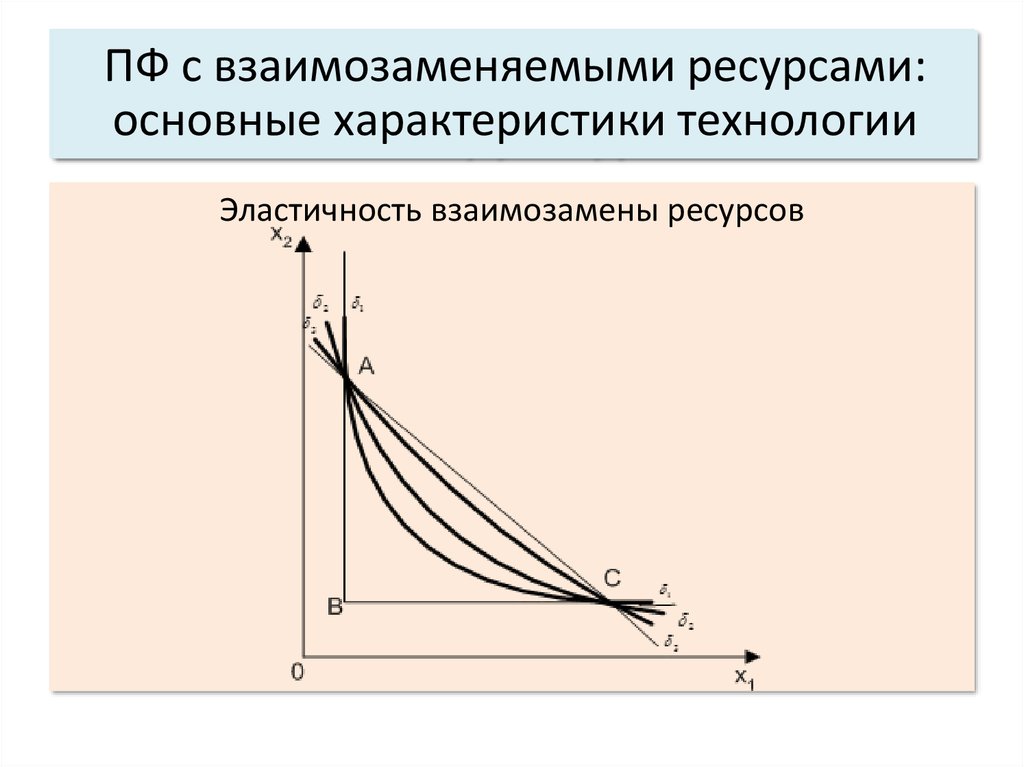
5. Эластичность взаимозамены ресурсов.
Коэффициент эластичности взаимозамены ресурсов
показывает, на сколько изменится соотношение затрат
ресурсов факторов производства при изменении
предельной нормы их взаимозамены на 1% при
сохранении объема производства.
xxkl MRTS kl
xxkl
xl
kl xk :
.MRTS kl
MRTS kl
MRTS kl
xk
xl
Чем выше эластичность замены ресурсов, тем в более
широких пределах они могут заменять друг друга.

17. Основные характеристики системы: 3. Структура.

Основные
характеристики
системы:
ПФ с взаимозаменяемыми
ресурсами:
основные характеристики
3. Структура.технологии
Эластичность взаимозамены ресурсов

18. 3.3. Производственные функции с взаимодополняемыми ресурсами и функции производственных затрат

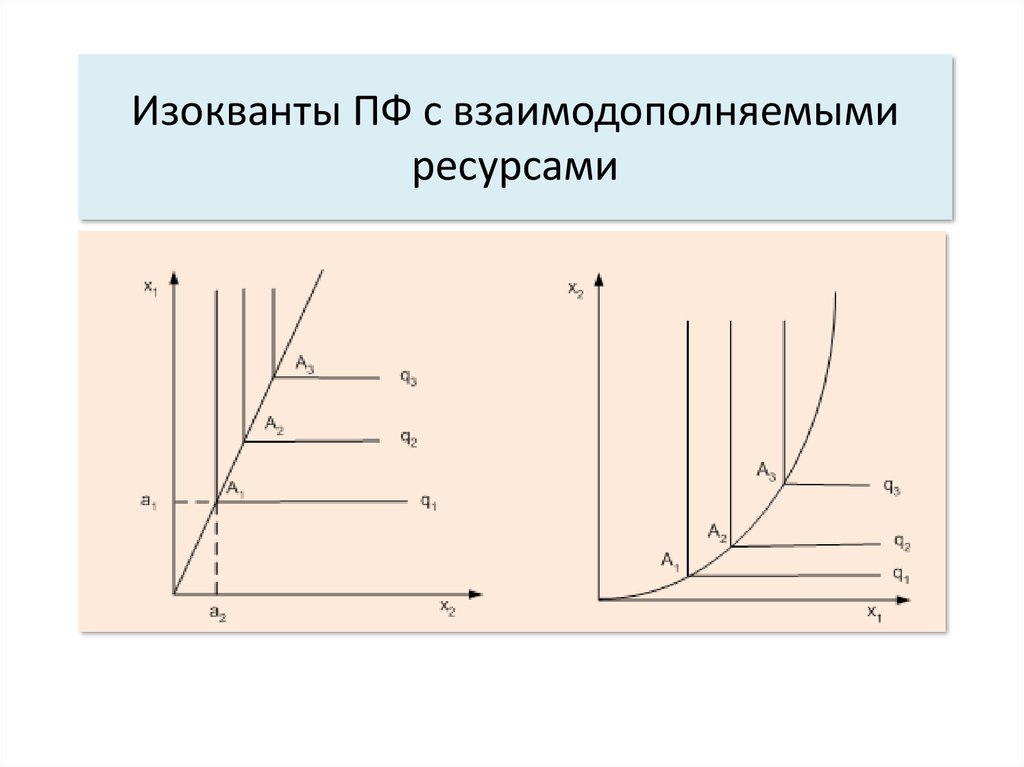
19. Общий вид ПФ с взаимодополняемыми ресурсами

где fs(xs) - объем производства, который может быть
получен при использовании s-ro ресурса в количестве
xs при условии, что другие ресурсы имеются в
достаточном количестве. Максимальный объем
производства определяется «узким местом», т.е.
количеством такого ресурса, который обеспечивает
наименьший объем производства.

20. Изокванты ПФ с взаимодополняемыми ресурсами

21. Основные характеристики системы: 2. Функция и цель.

Основные характеристики системы:
Функции производственных затрат
2. Функция и цель.
Функция
xi = φi (y)
называется функцией производственных затрат
ресурса i. Показывает минимальное количество
ресурса i, которое нужно затратить для выпуска
продукта в количестве у.
Функции производственных затрат являются
обратными к производственным функциям с
взаимодополняемыми ресурсами.

22. Функции производственных затрат

Основные характеристики:
• cредние затраты i-ro ресурса: qi = xi/y;
• предельные затраты i-ro ресурса: hi = dxi/dy;
характеризуют прирост затрат ресурса i при
увеличении выпуска продукции на малую
единицу.
Соотношения
между
средними
и
предельными затратами зависят от свойств
функции х = φ(y).

23. 3.4. Типовые производственные функции

24. Основные характеристики системы: 3. Структура.

Основные характеристики системы:
Степенная производственная функция
3. Структура.
Общий вид:
Пример: функция Кобба-Дугласа

25. Основные характеристики системы: 3. Структура.

Основные характеристики системы:
Степенная производственная функция
3. Структура.
Свойства степенной функции:
1. Функция является однородной.
Функция у = f(X) называется однородной n-й степени, если
для любого λ выполняется соотношение:
Это означает, что при увеличении затрат всех ресурсов в
λ раз объем производства возрастает в λn раз.
Показатель степени однородности n характеризует
изменение эффективности производства с увеличением
производственных затрат (эффект масштаба).

26. Основные характеристики системы: 3. Структура.

Основные характеристики системы:
Степенная производственная функция.
3. Структура.
Свойства степенной функции:
2.
Предельная
ресурсов:
норма
эквивалентной
замены
3. Коэффициент эластичности выпуска по i -му ресурсу
δi = αi;
4. Коэффициент эластичности замены ресурсов σkl = 1.
5. Изоклиналь — луч, исходящий из начала координат.

27. Основные характеристики системы: 3. Структура.

Основные
системы:
Функция с характеристики
постоянной эластичностью
замены
ресурсов
3. Структура.
Общий вид:
Пример: функция Солоу

28. Основные характеристики системы: 3. Структура.

Основные
системы:
Функция с характеристики
постоянной эластичностью
замены
ресурсов
3. Структура.
В функции CES все эластичности замены ресурсов σkl равны
между собой: σkl = σ, при этом
.
При σ = 1 (ρ → 0) функция CES преобразуется в степенную
производственную функцию.

29. Основные характеристики системы: 3. Структура.

Основные характеристики системы:
Функция Леонтьева
3. Структура.
Производственная функция Леонтьева относится
к классу функций с взаимодополняемыми
ресурсами и имеет вид:
Y = min{aK, bL}.
Изокванты ПФ Леонтьева имеют вид прямых
углов. Вершины углов имеют координаты L = C/b,
K = C/a, где С – значение производственной
функции, соответствующее данной изокванте.