Похожие презентации:
Твердотельная электроника. Полупроводниковые диоды
1.
Электронный учебно-методическийкомплекс
Твердотельная электроника
Презентации к лекционному курсу
Полупроводниковые диоды
МОСКВА
2012
НИУ «МЭИ»
2. Уравнения непрерывности
3. ПРИНЯТЫЕ ДОПУЩЕНИЯ ПРИ РАСЧЁТЕ ВАХ
Модель электронно-дырочного перехода одномерная; p- и
n-области имеют бесконечную протяженность.
Переход тонкий, носители заряда пролетают через ОПЗ
без рекомбинации (ОПЗ стянут в линию).
Обе квазинейтральные области сильно легированы,
падением напряжения на них можно пренебречь. Вся
внешняя разность потенциалов приложена к pn-переходу.
Рекомбинацию считаем линейной.
Уровень инжекции мал (Δnp<<pp0, Δpn<< nn0).
4.
Но в квазинейтральной области напряженность внешнегоэлектрического поля равна нулю!
Таким образом, плотность тока в n-области определяется
диффузионным током дырок, зависящим от их градиента
концентрации:
p n
pn pn0
2 p n
Dp
0
2
t
p
x
d 2 p n p n
2 0
2
dx
Lp
Lp D p p
Общее решение такого уравнения имеет вид:
p n A exp x L p B exp x L p
5.
p n p n 0 pn pn 0 A exp x L pКонцентрация неравновесных дырок на границе ОПЗ
при x=Wn равна:
Vсм
p n Wn p no exp
T
При x=Wn:
Vсм
A p no exp
T
Wn
1 exp
L
p
.
6.
Окончательнозакон
изменения
концентрации
неравновесных дырок в n-области при x>Wn принимает вид:
x Wn
pn x pn 0 pn pn 0 pn 0 pn 0 exp
L
p
x Wn
Vсм
1 exp
pn 0 pn 0 exp
L
p
T
x Wn
Vсм
1 1 exp
pn 0 exp
L
T
p
7.
j p j p дифn
jp
dp
q D p
dx
x Wn
q D p pn 0 Vсм
1 exp
exp
Lp
L
p
T
На границе ОПЗ при x=Wn, получим:
n
jp
q D p pn 0 Vсм
1 .
| x Wn
exp
Lp
T
8.
Аналогично для p-области при x < -Wp:Vсм
x Wp
1 exp
n p x n p 0 n p 0 exp
Ln
T
Vсм
x W p
1 1 exp
n p 0 exp
Ln
T
p
jn
q Dn n p 0 Vсм
x Wp
1 exp
exp
Ln
Ln
T
9. Решение уравнения для ВАХ
10.
ВАХ тонкого pn-перехода описывается уравнением:Dn n p 0 D p pn 0 Vсм
Vсм
exp
1 J s exp
1 .
j q
Lp T
T
Ln
известным как формула Шокли.
где
Dn
q Dn n p q D p pn
Dp
2
js jsn jsp
q ni
Ln
Lp
Ln N a Lp N d
n p Ln pn Lp
q
p
n
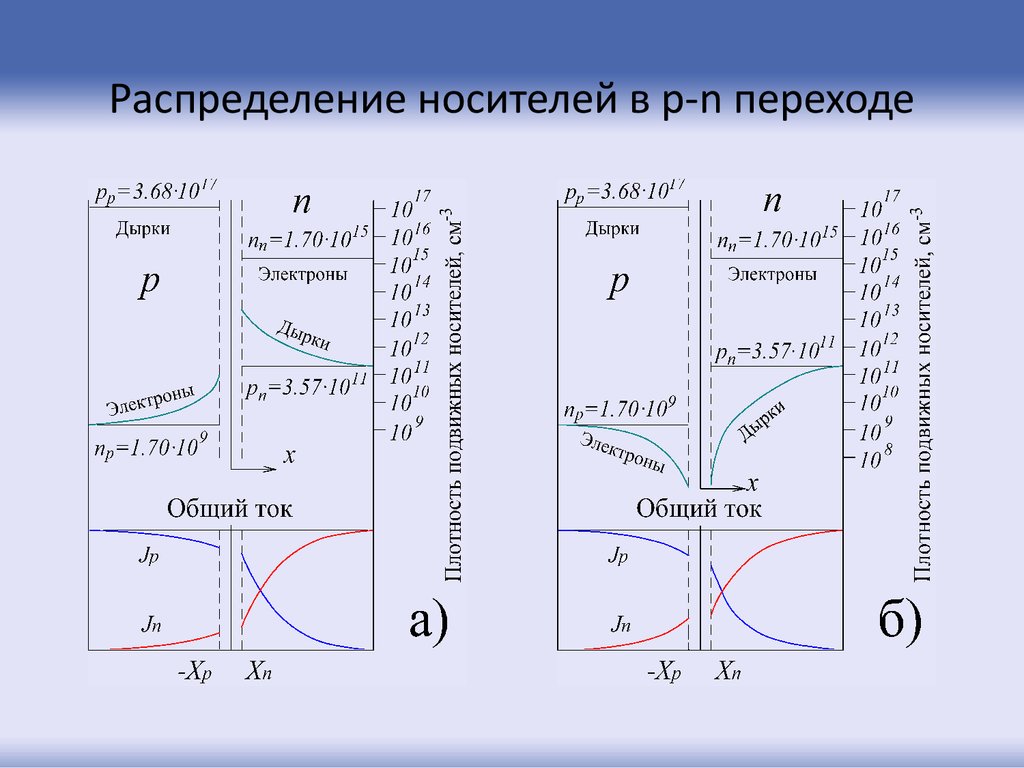
11. Распределение носителей в p-n переходе
12.
njp
p
jn
x
q D p pn 0
exp
Lp
Lp
q Dn n p 0
x
exp
Ln
Ln
j s j sn j sp
q Dn n p
Ln
q D p pn
Lp
.
13.
Расчет для кремниевого p-n-перехода18
15
-3
-3
cм
p
N
10
n
N
10
Пусть po
cм , no
a
d
2
n
10
Тогда po
cм-3 ,
pno 105 cм-3
При прямом смещении:
Пусть Vсм 0.6
Vсм
600
10
10
B , тогда exp exp
26
Т
Vсм
15
-3
pn Wn pno exp
10
cм
и равна nno
Т
Vсм
1012 cм-3
n p W p n po exp
Т
14.
При обратном смещении:Уже при Vсм 3 T 78 мB exp - 3 0.05
т.е. граничные концентрации составляют 5% от исходных.
n po n p
и
pno pn
x
Vсм
1 exp
pn x pn 0 exp
L
T
p
Vсм
x
1 exp
n p x n p 0 exp
Ln
Т
15.
j pSq Dn n p 0
jnS
Ln
q D p pn0
Lp
D p 2.5 см2/с
Dn 25 см2/с
Lp 14 10 см
Ln 20 10 4 см
4
10
j pS 0.3 10 А/см
2
jnS 2 10 13 А/см2
Vсм
0.3 10 10 1010 0.3 А/см2
j p j pS exp
T
Vсм
2.3 10 13 1010 2 10 3 А/см2
jn jnS exp
T
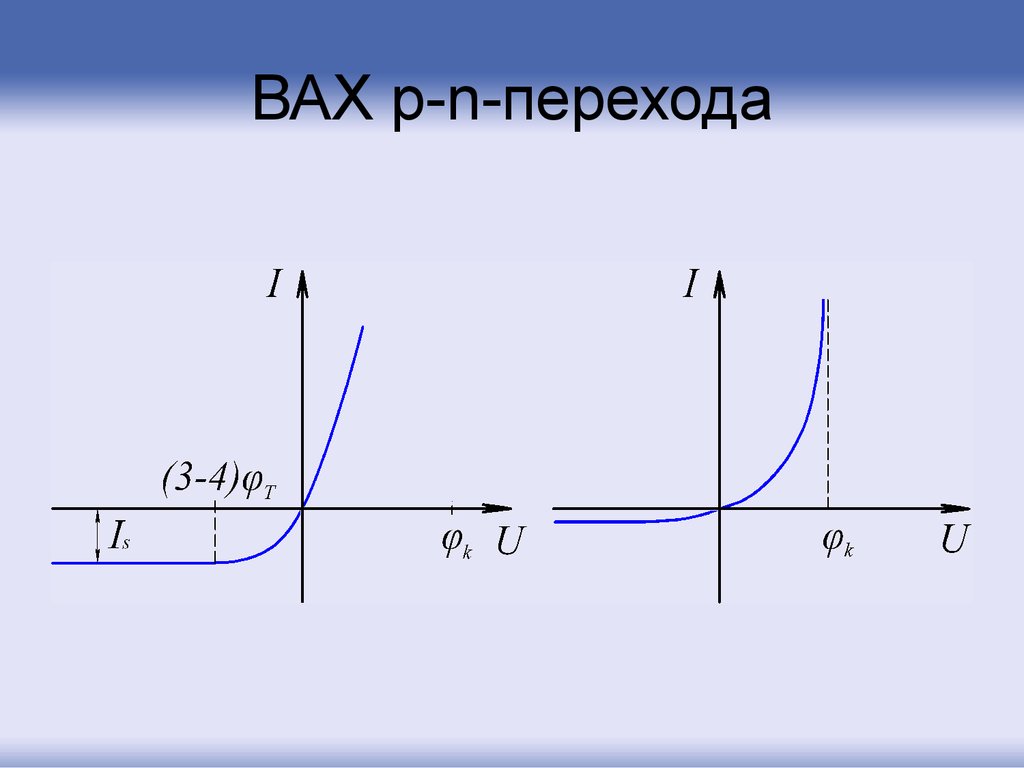
16. ВАХ p-n-перехода
17.
Оценим, насколько справедливо в нашем примерепредположение, что напряжение смещения приложено
только к pn-переходу. Для полученного полного тока
определим падение напряжения на толще n- и p-областей,
приняв длину n-области ln =0,01 см, длину p-области за
1 мкм=10-4 см. Проводимости σ n=q∙μn∙n, σp =q∙μp∙p.
Подвижности μn и μp зависят от концентраций примеси в
полупроводниках, исходя из данных, приведенных в
литературе: μn = 300 см2/В∙с, μp =100 см2/В∙с.
1
19
15
2
σn=q∙μn∙n= 1,6 10 10 300 4,8 10 Ом см
σp=q∙μp∙p= 1,6 10 19 1018 100 16 Ом см 1
Падение напряжения на n- и p-слоях
Vn
j
0,3 10 0,01
ln
0,0625В
n
4,8
2
0,3 10 2 10 4
Vp
lp
0,0002 В
p
16
j
18.
Прямое смещение p-n-перехода19.
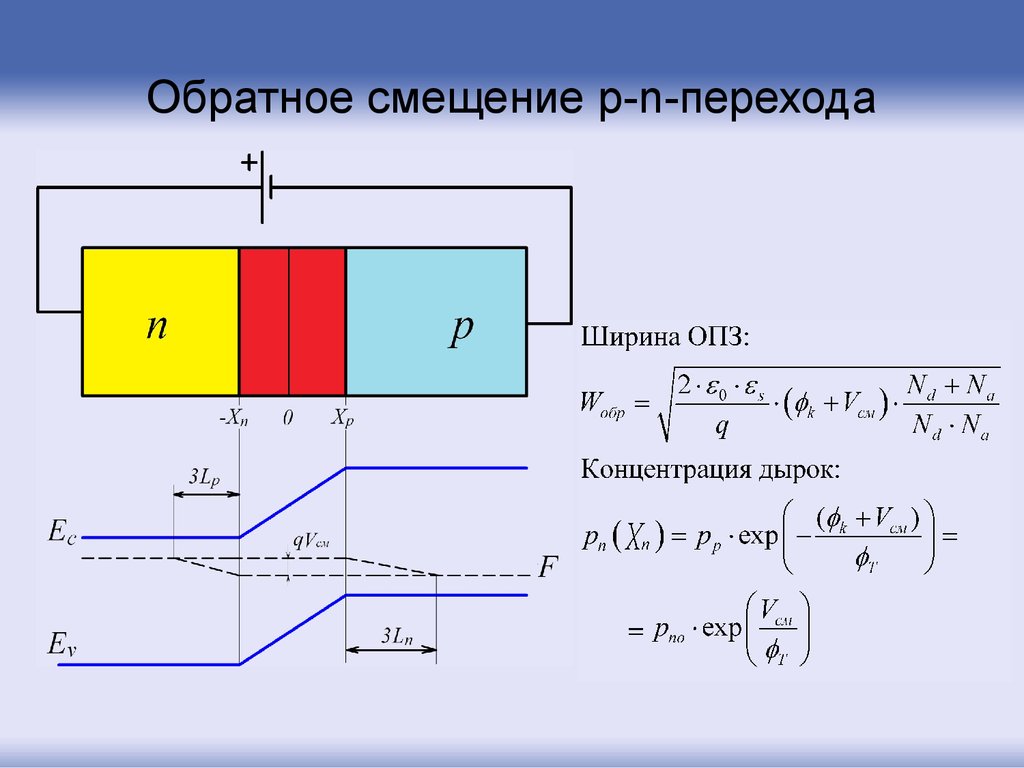
Обратное смещение p-n-перехода20.
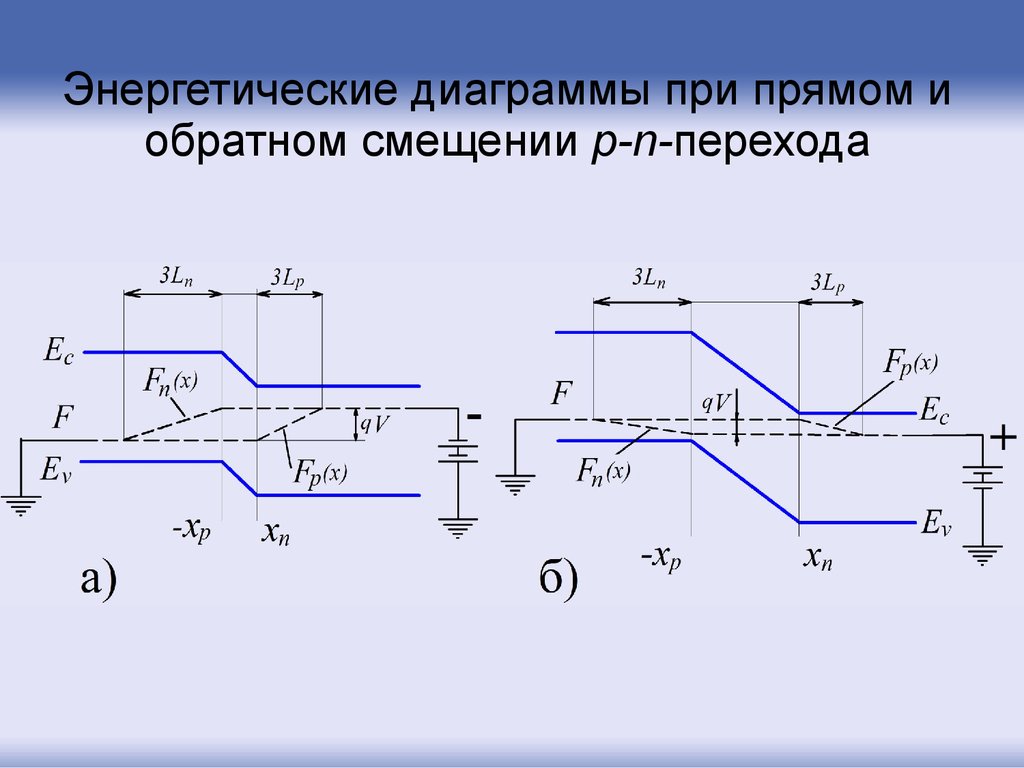
Энергетические диаграммы при прямом иобратном смещении p-n-перехода
21. Влияние различных факторов на ВАХ pn-перехода
E g Тni N c Т N v Т exp
2kT
js jsn jsp
q Dn n p
Ln
q D p pn
Lp
Dn
Dp
q n
L N
n a Lp N d
Nd Na
k Т ln
n i2
2
i
.
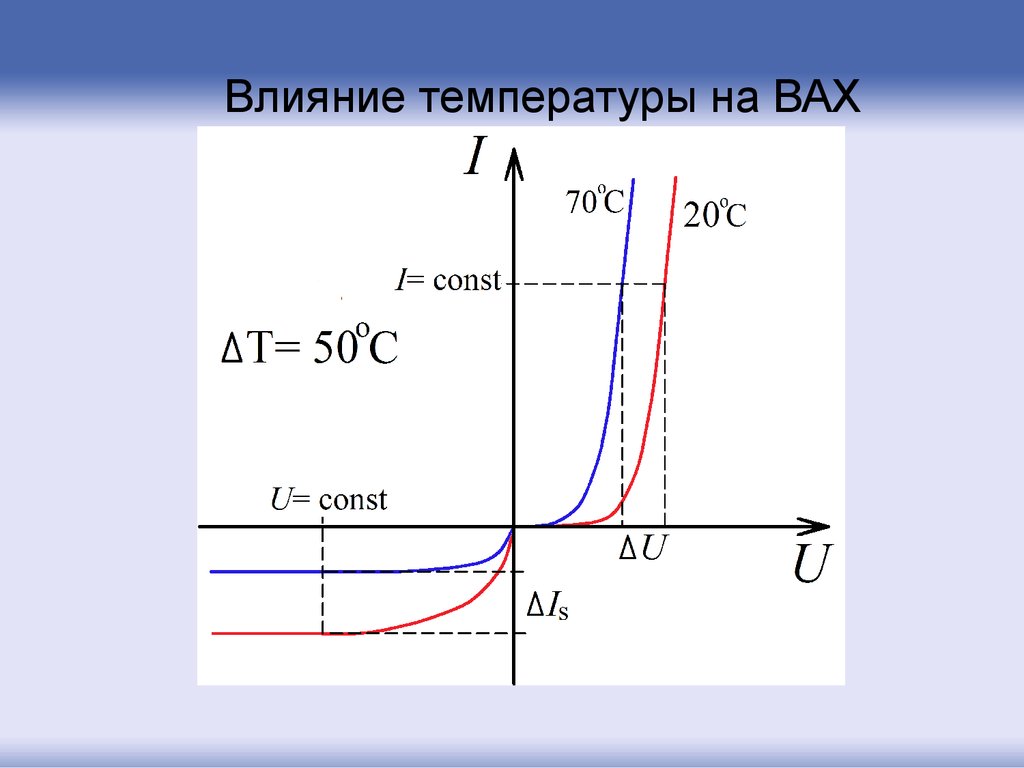
22.
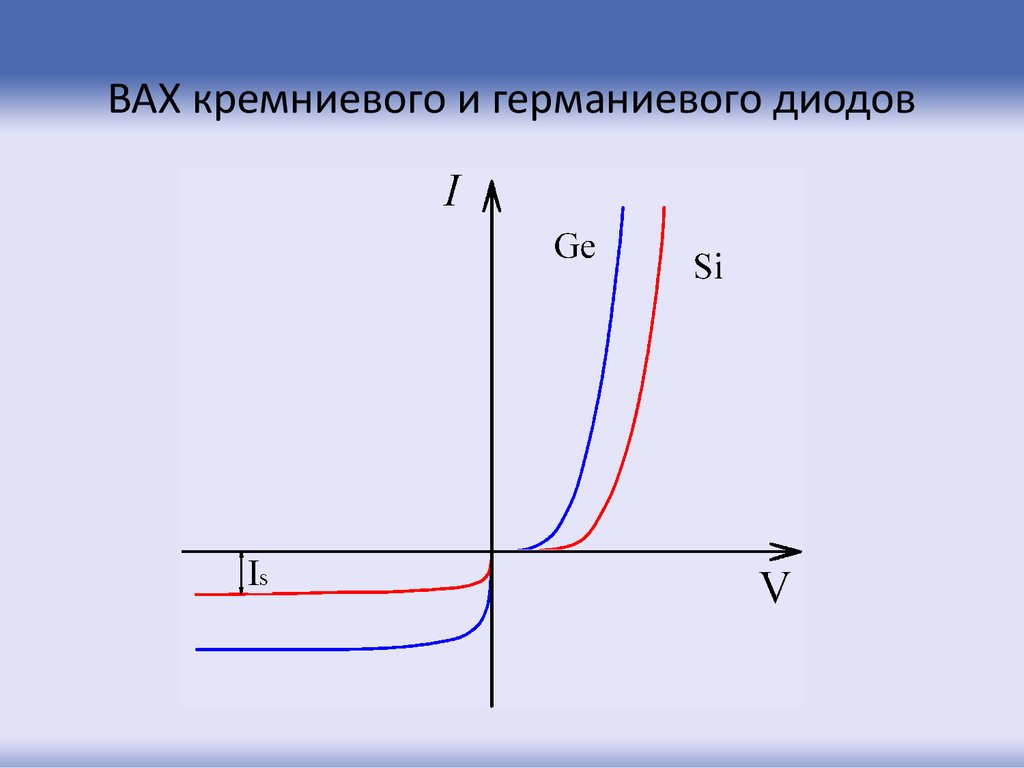
Влияние температуры на ВАХ23. ВАХ кремниевого и германиевого диодов
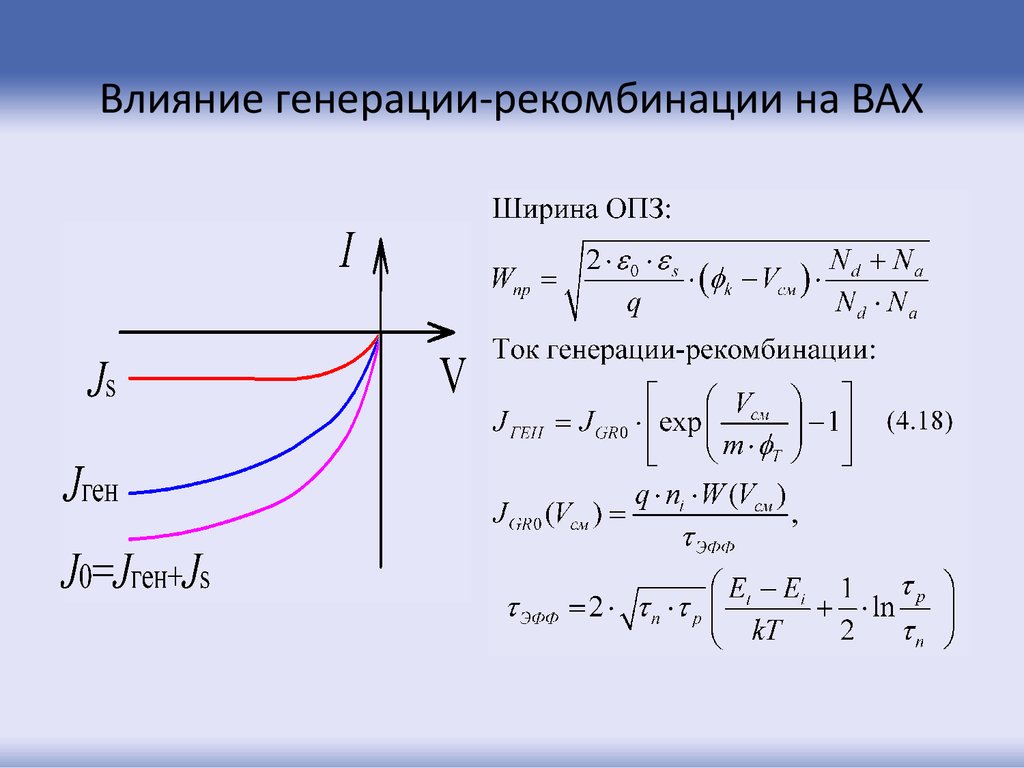
24. Влияние генерации-рекомбинации на ВАХ
25.
effp
n p ln , если Et Ei
n
– прямое смещение pn-перехода:
пр n p
– обратное смещение pn-перехода:
обр n p
26.
Емкостные свойстваpn-перехода
27.
К расчету емкости p-n-переходаПри нулевом смещении на рп-переходе:
2 0 s N d N a
W0
k
q
Nd Na
Wn
2 0 s
Na
2 0 s
Nd
k
;W p
k
Nd Na Nd
Nd Na Na
q
q
При обратном смещении:
Wобр
Wn
2 0 s
N Na
k Vсм d
q
Nd Na
2 0 s
Na
2 0 s
Nd
k Vсм
;W p
k Vсм
Nd Na Nd
Nd Na Na
q
q
28.
Из формулы для плоскогоконденсатора:
Cбар
0 s S
0 s q
Nd Na
S
W
2 k Vсм N d N a
При Na>>Nd:
Cбар
0 s q
S
Nd
2 k Vсм
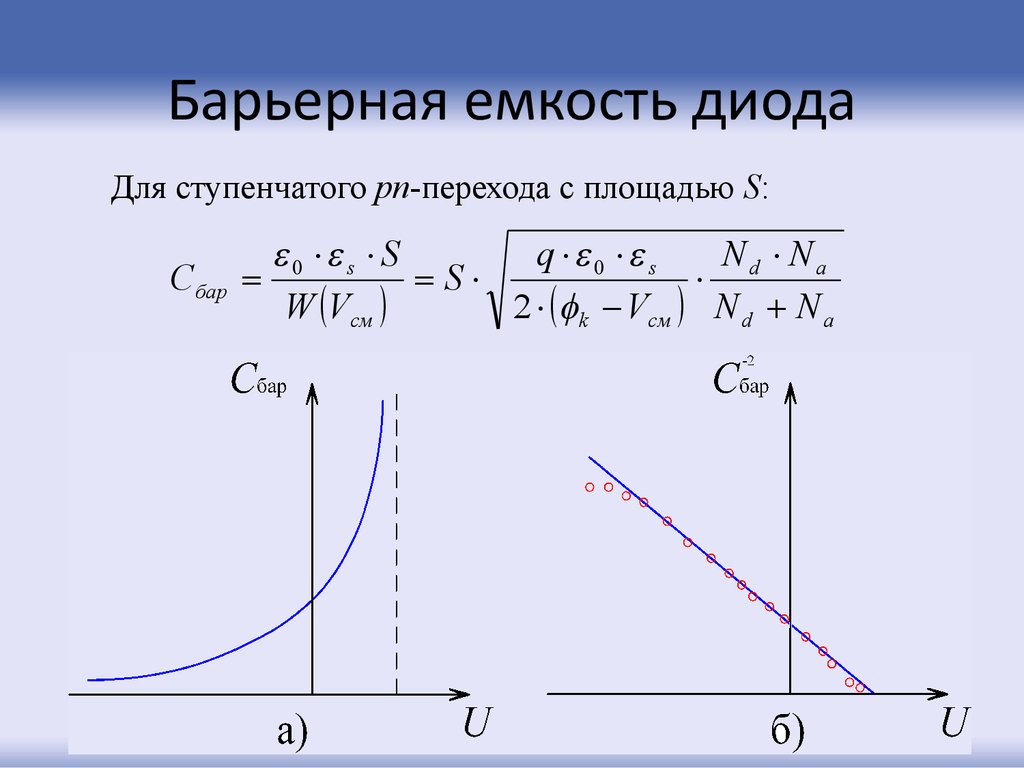
29. Барьерная емкость диода
Для ступенчатого pn-перехода с площадью S:С бар
0 s S
q 0 s
Nd Na
S
W Vсм
2 k Vсм N d N a
30.
Емкость pn-перехода может изменяться в значительныхпределах, что позволило использовать это свойство в
варикапах.
Варикап – нелинейный управляемый конденсатор, емкость
которого изменяется в зависимости от обратного напряжения. В
варикапах используется барьерная емкость, не зависящая от
частоты вплоть до миллиметрового диапазона, имеющая малый
температурный коэффициент емкости.
Варикап обладает высокой стабильностью параметров во
времени. В радиоэлектронных устройствах варикапы
применяют в усилителях, умножителях частоты, смесителях,
детекторах и в схемах с электронной настройкой.
31. Диффузионная емкость pn-перехода
dQCдиф
dV
где Q – инжектированный заряд.
Cдиф
( I p p I n n )
T
S
j p p jn n
T
Полная емкость pn-перехода равна сумме барьерной и
диффузионной емкостей. При прямых напряжениях барьерная
емкость много меньше диффузионной, а при обратных
напряжениях она значительно превышает ее. Соотношения
между барьерной и диффузионной емкостью определяют
частотные зависимости pn-перехода.
32. Пробой p-n-перехода
33. Обратная ВАХ при различных видах пробоя
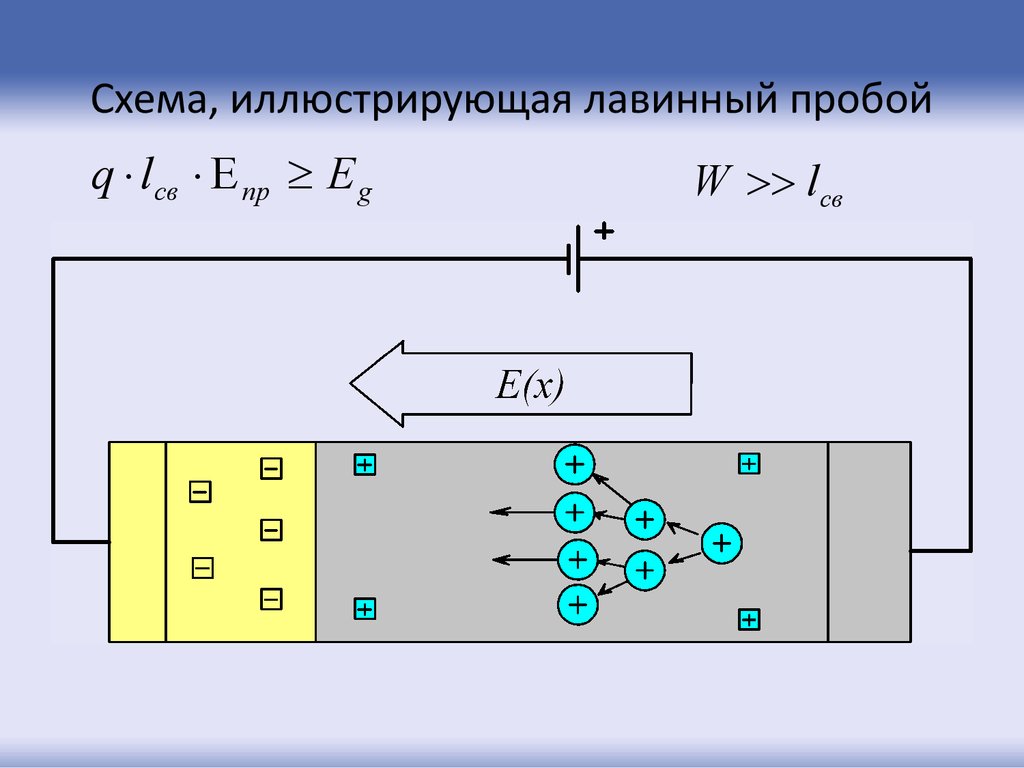
34. Схема, иллюстрирующая лавинный пробой
q l св пр Е gW l св
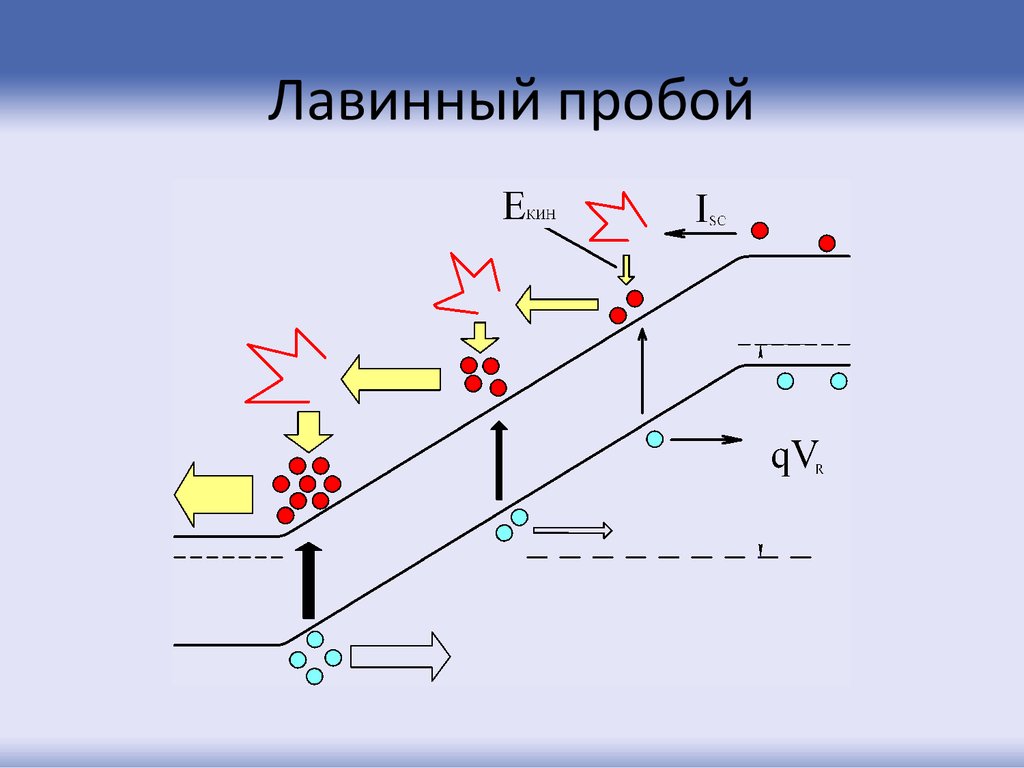
35. Лавинный пробой
36.
Коэффициент лавинного умножения M, определяемый какколичество актов лавинного умножения в области сильного
электрического поля, для которого справедливо следующее
эмпирическое соотношение Миллера:
Vсм
J
M 1
J 0 Vпроб
n 1
37.
Напряжение лавинного пробоя зависит от степенилегирования p- и n-областей. Так, например для резкого
кремниевого p-n-перехода зависимость напряжения пробоя от
степени легирования n-области имеет вид:
32
Vпроб
Eg N
60 16
1.1 10
3 4
Напряжение лавинного пробоя кремниевого pn-перехода
с линейным распределением примеси (то есть при изменении
примеси по линейному закону) определяется формулой:
1, 2
Vпроб
0 , 4
E
g a
60
,
20
1.1 3 10
где а – градиент концентрации примеси
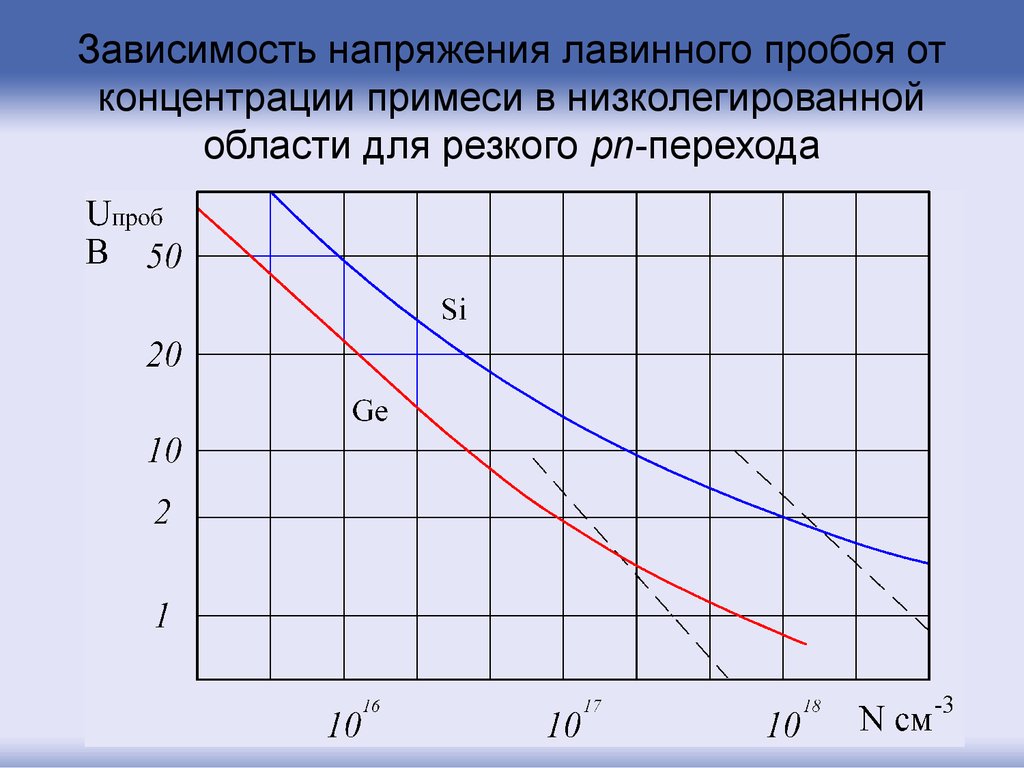
38. Зависимость напряжения лавинного пробоя от концентрации примеси в низколегированной области для резкого pn-перехода
39.
Температурная зависимость напряжения лавинногопробоя определяется уменьшением длины свободного пробега
носителей заряда с увеличением температуры.
При этом величина напряжения пробоя увеличивается,
так как энергию, необходимую для разрыва ковалентных
связей носители могут набрать при больших напряжениях.
40.
Туннельныйпробой pn-перехода
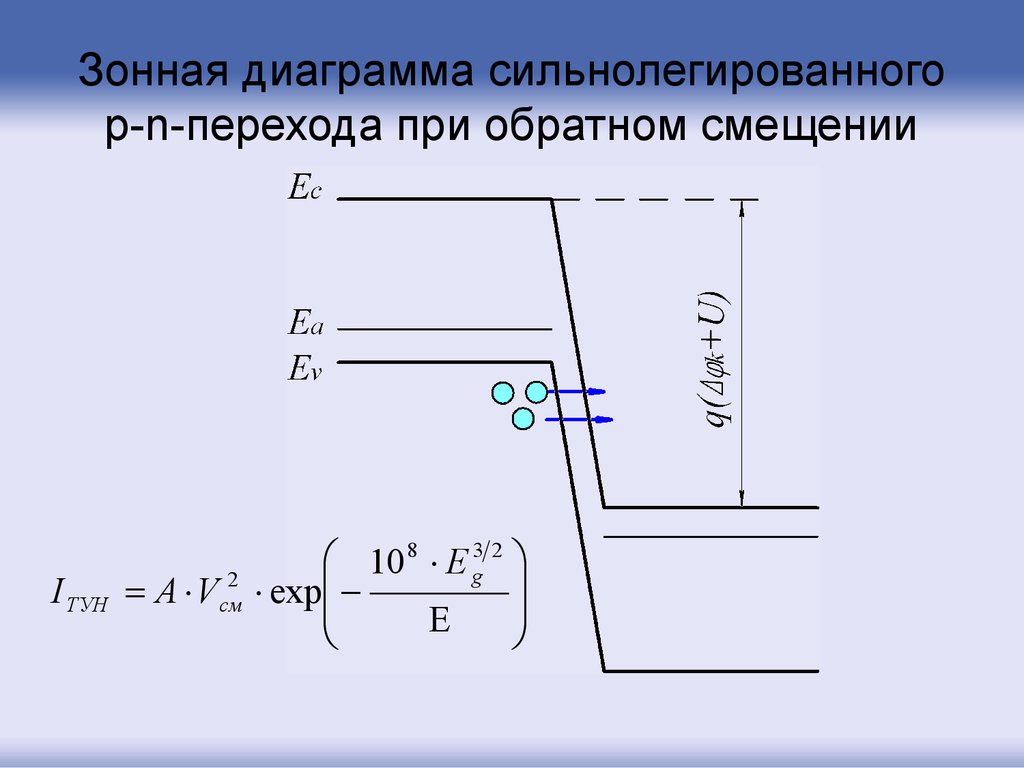
41. Зонная диаграмма сильнолегированного p-n-перехода при обратном смещении
I ТУН8
32
10
E
g
A Vсм2 exp
42.
Чтобы этот эффект имел место, электрическое поледолжно быть настолько сильным, чтобы обеспечить такой
наклон зон, при котором заполненные электронами уровни
валентной зоны оказались напротив незаполненных
энергетических уровней разрешенной зоны, а ширина
потенциального барьера сравнима с длиной волны де Бройля
электрона.
43.
Напряжение туннельного пробоя сравнительно слабозависит от температуры. Однако с ростом температуры
ширина запрещенной зоны германия и кремния уменьшается,
вероятность туннелирования возрастает, и величина
критической напряженности поля уменьшается. Поэтому
напряжение туннельного пробоя уменьшается.
Поскольку напряжение, при котором возникает лавинный
и туннельный пробой достаточно стабильно, этот эффект
используется для создания приборов, падение напряжения на
которых остается стабильным при изменении тока –
стабилитронов.
44.
Тепловой пробой pn-переходаПри увеличении обратного напряжения увеличивается
мощность, рассеиваемая в переходе в виде тепла, поэтому
для pn-переходов со сравнительно высокими обратными
токами возможен разогрев.
Начавшийся разогрев, в свою очередь,
увеличению обратного тока. Таким образом, в
возникает положительная обратная связь,
возникновению тепловой неустойчивости –
пробою.
приведет к
pn-переходе
ведущая к
тепловому
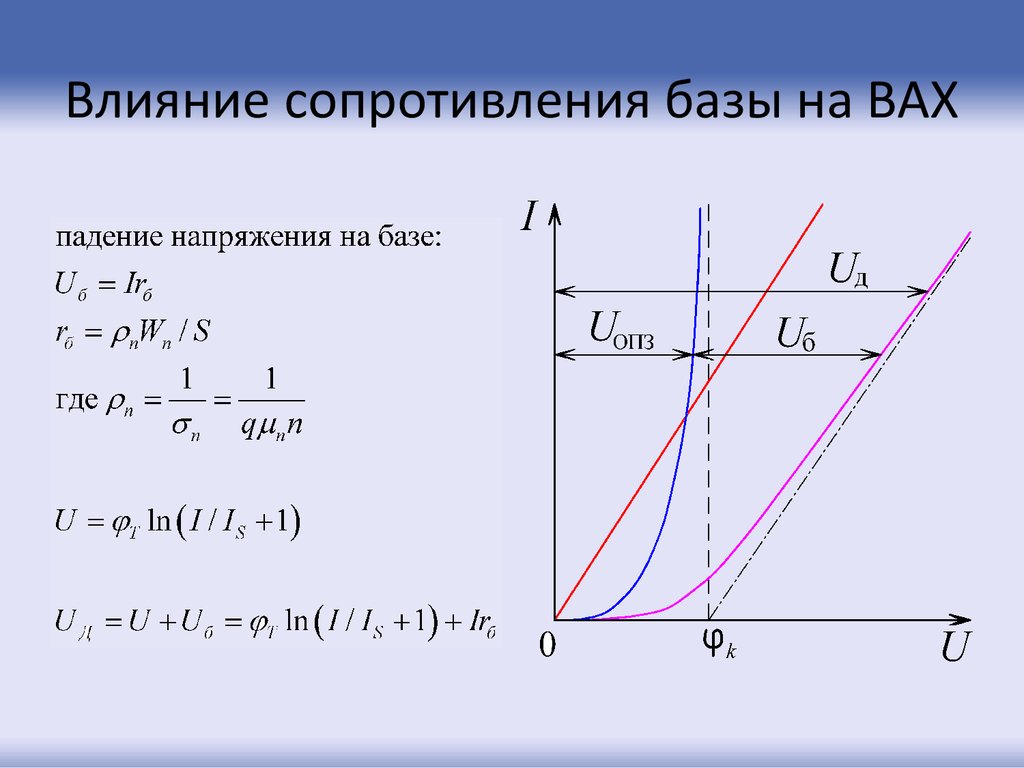
45. Влияние сопротивления базы на ВАХ
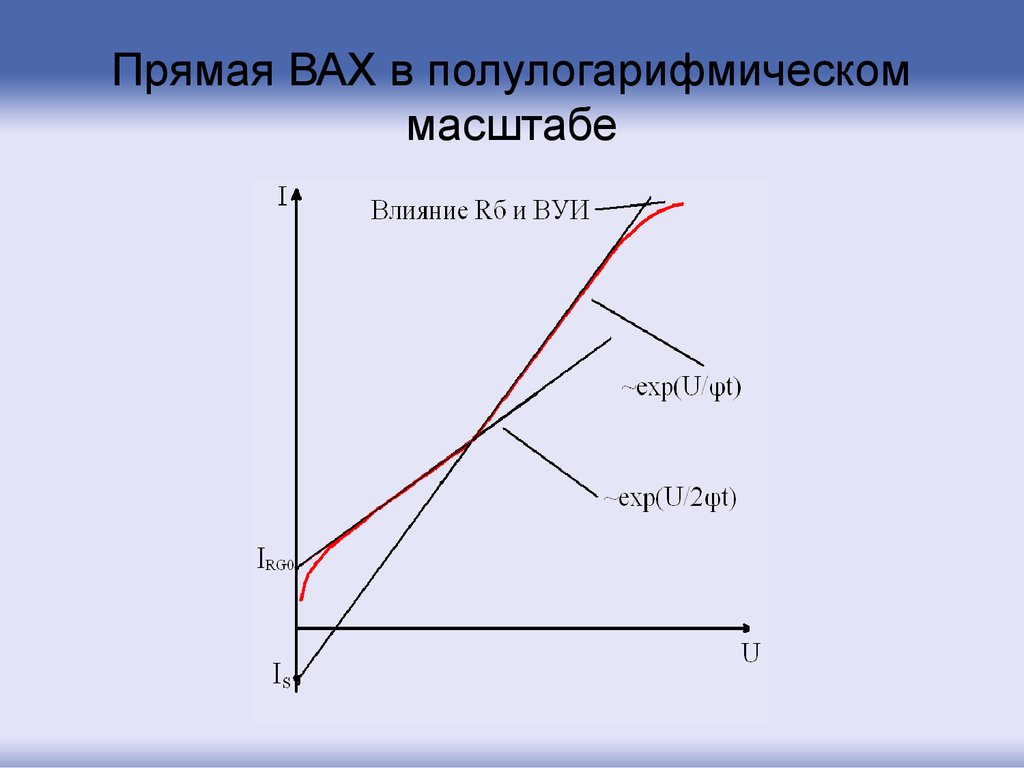
46. Прямая ВАХ в полулогарифмическом масштабе
47.
l n Wn Vcм , в свою очередь, влияет наТолщина базы
закон распределения инжектированных носителей и
диффузионных токов.
Экспоненциальное распределение, представленное
формулах справедливо для длинной базы, то есть при
l n Wn Vcм L p
В случае короткой базы:
pn x pn0
x n Wn x
sh
Lp
p n 0
x n Wn
sh
Lp
x
p n x p n 0 p n 0 1
xn Wn
в
48. Характеристическое сопротивление диода
Различают два вида характеристического сопротивлениядиодов: дифференциальное сопротивление rd и сопротивление по
постоянному току RD.
Дифференциальное сопротивление определяется как
1
dVсм dI
rd
dI
dVсм
1
1
Is
V см I s I s
I Is
T
exp
I Is
Т T T
T
T
49.
Сопротивление по постоянному току R DОпределяется как отношение приложенного напряжения к
протекающему току через диод:
RD
Vсм
I
Vсм
Vсм
1
I s exp
Т
На прямой ВАХ сопротивление RD >rd, на обратной – RD <rd.
В точке вблизи нулевого значения напряжения Vсм kT q
значения сопротивлений совпадают.
Действительно, разложив экспоненту, получаем:
1 kT 1
R D T
rd
Is
q Is
50.
Переходные процессыв полупроводниковых диодах
При
быстрых
изменениях
напряжения
на
полупроводниковом диоде значение тока через диод,
соответствующее статической ВАХ, устанавливается не сразу.
Процесс установления тока при таких переключениях называют
переходным процессам.
Переходные процессы в полупроводниковых диодах
связаны с накоплением носителей в базе диода при его прямом
включении и их рассасывании в базе при быстром изменении
полярности напряжения на диоде. Так как электрическое поле в
базе обычного диода отсутствует, то движение неосновных
носителей в базе определяется законами диффузии и происходит
относительно медленно. В результате кинетика накопления
носителей в базе и их рассасывание влияют на динамические
свойства диодов в режиме переключения.
51.
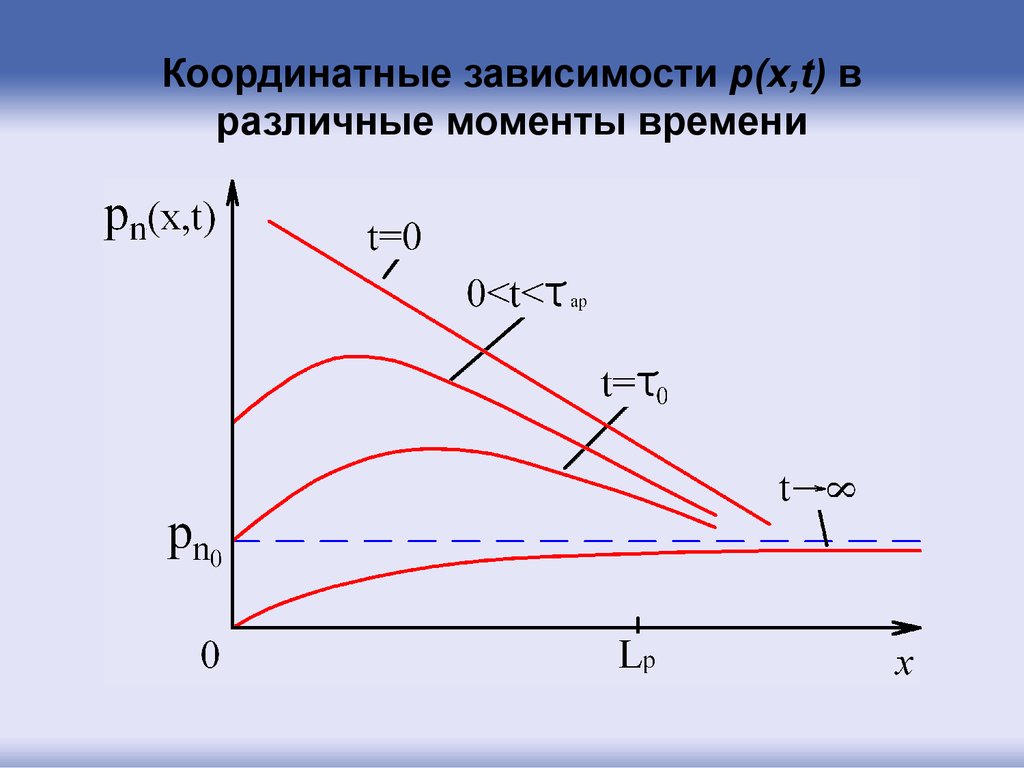
Приt 0
x
pn x pn1 pn 0 exp pn 0
Lp
С течением времени концентрация неравновесных
носителей будет убывать, следовательно, будет убывать и
обратный ток.
За время τ0, называемое временем восстановления
обратного сопротивления или временем рассасывания,
обратный ток придет к значению, равному току насыщения.
При
t
x
p n p n 0 1 exp
L
p
52. Координатные зависимости p(x,t) в различные моменты времени
53.
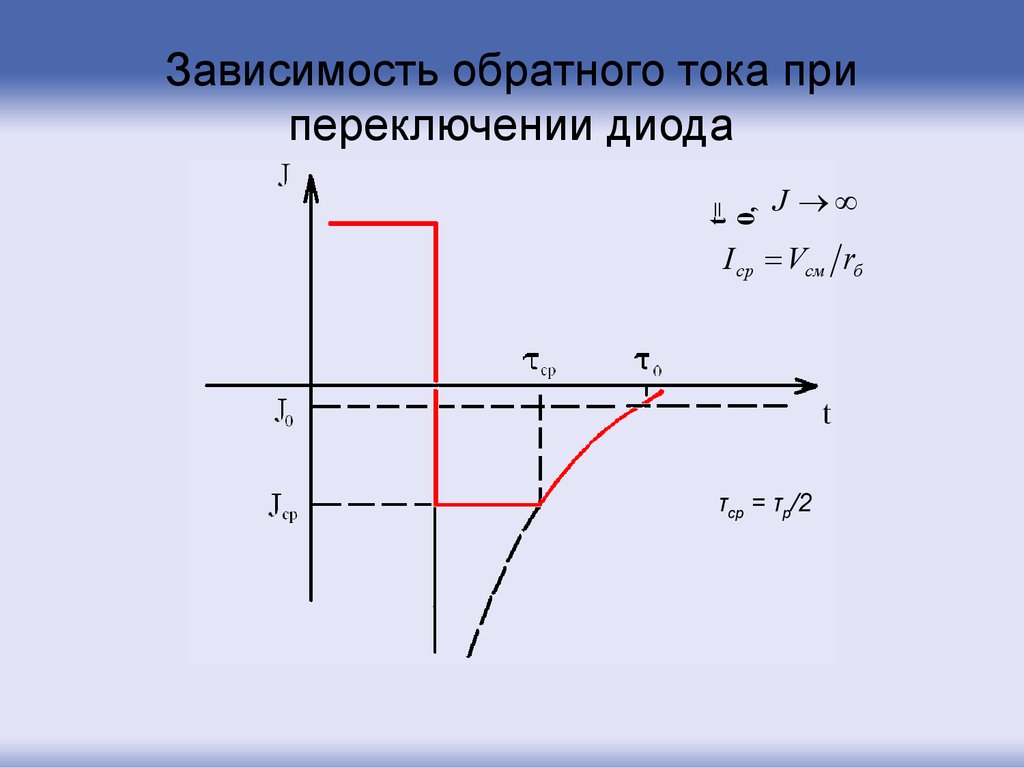
Обратный ток обусловлен только диффузией дырок кгранице ОПЗ p-n-перехода:
dp n
j qD p
| x 0
dx
54. Зависимость обратного тока при переключении диода
t=0,
Зависимость обратного тока при
переключении диода
J
I ср Vсм rб
τср = τр/2
55.
Полупроводниковые диодыВ данном разделе будут рассмотрены следующие типы
полупроводниковых диодов:
-выпрямительные диоды на основе pn-перехода
- стабилитроны, варикапы
-туннельные и обращенные диоды
56. Выпрямительные диоды
Основная задача выпрямительного диода – выпрямлениепеременного (в частности синусоидального) тока, то есть
выделение постоянной его составляющей.
Применяется в цепях управления и коммутации, для
развязок в электрических цепях, ограничения выбросов
напряжений в цепях с индуктивными элементами, а также в
цепях, где необходимы вентильные элементы и не
предъявляется жестких требований к временным и частотным
параметрам.
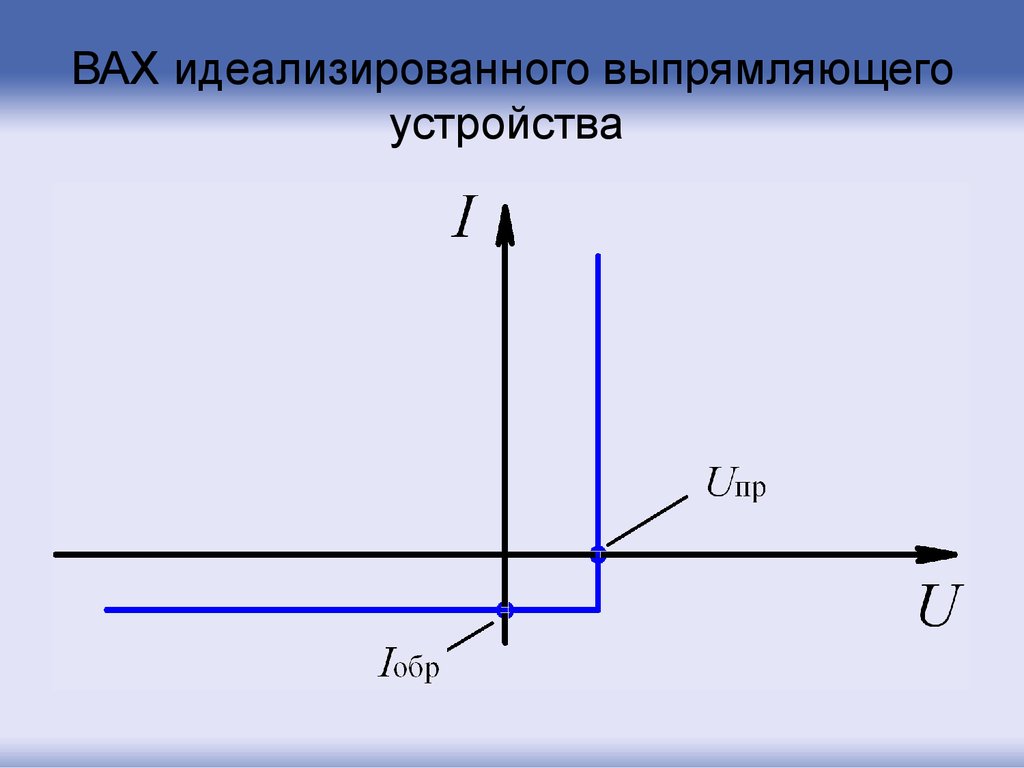
Выпрямительные
или
вентильные
свойства
полупроводникового диода определяются его ВАХ
57. ВАХ идеализированного выпрямляющего устройства
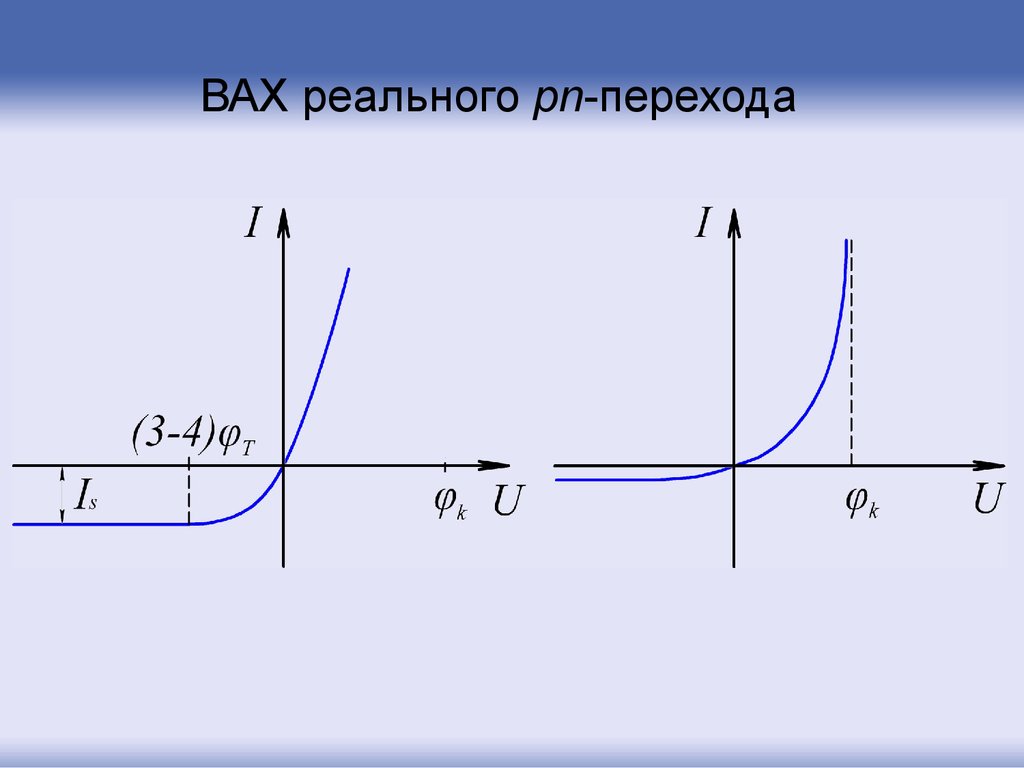
58. ВАХ реального pn-перехода
59.
Выпрямительный, или силовой, диод – прибор,предназначенный для выпрямления переменного тока. Их
применяют в цепях управления и коммутации, для
развязок в электрических цепях, ограничения выбросов
напряжений в цепях с индуктивными элементами, а также
в цепях, где необходимы вентильные элементы и не
предъявляется жестких требований к временным и
частотным параметрам.
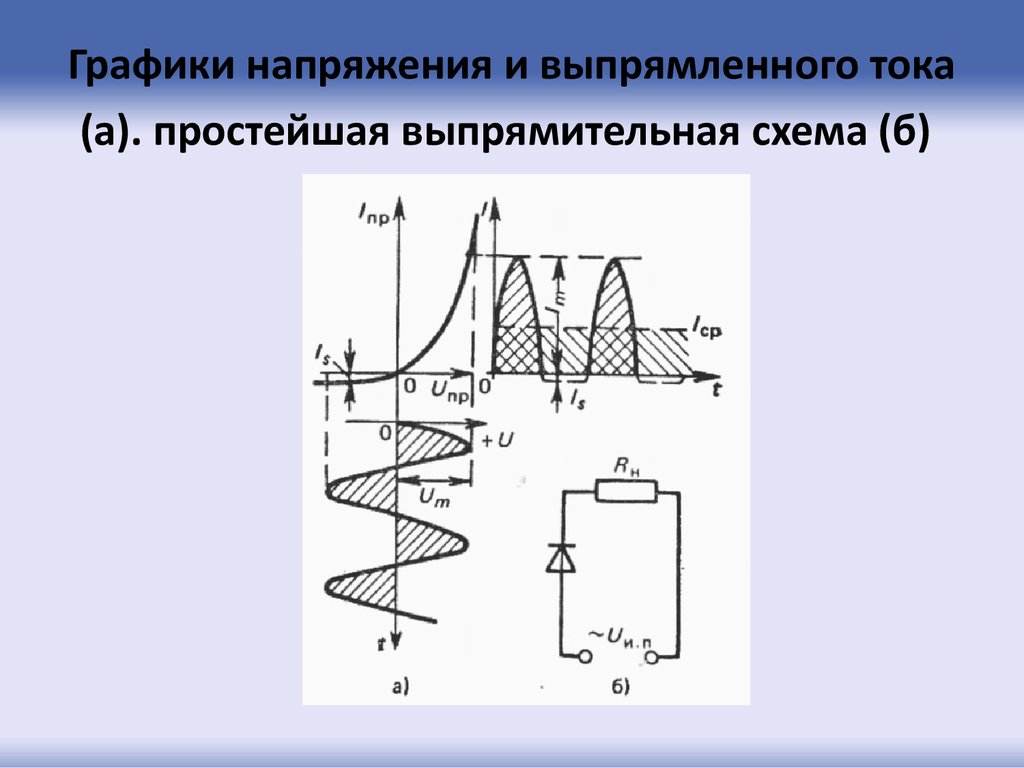
60. Графики напряжения и выпрямленного тока (а). простейшая выпрямительная схема (б)
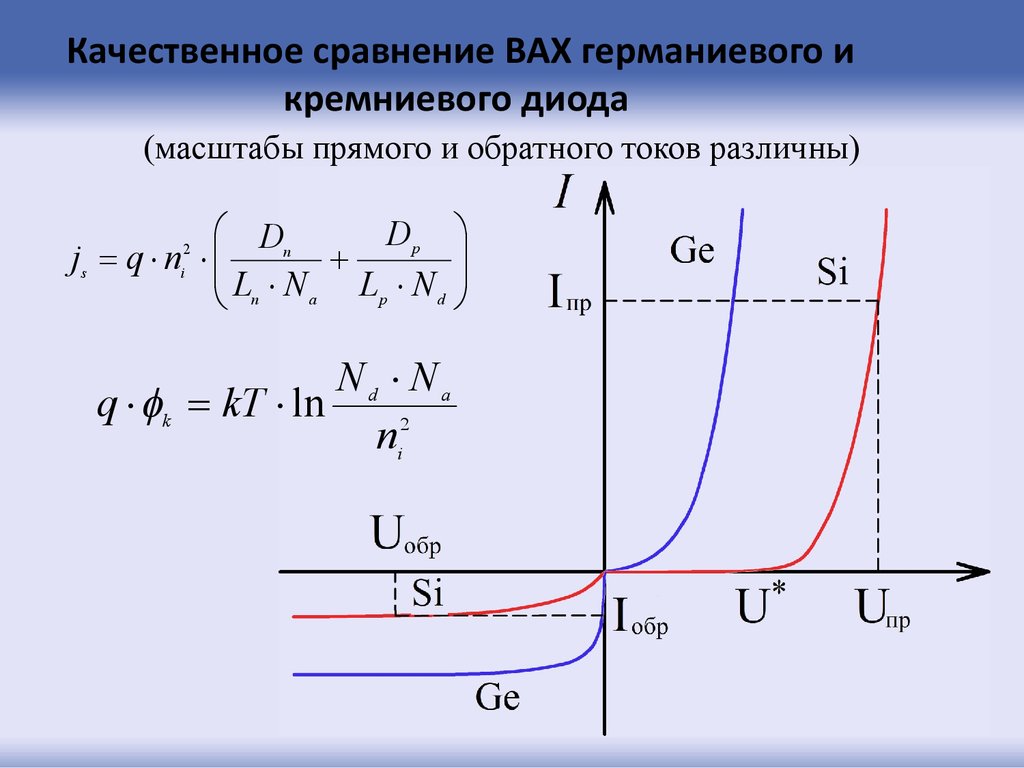
61. Качественное сравнение ВАХ германиевого и кремниевого диода (масштабы прямого и обратного токов различны)
DnDp
js q ni
Ln N a Lp N d
2
Nd Na
q k kT ln
ni2
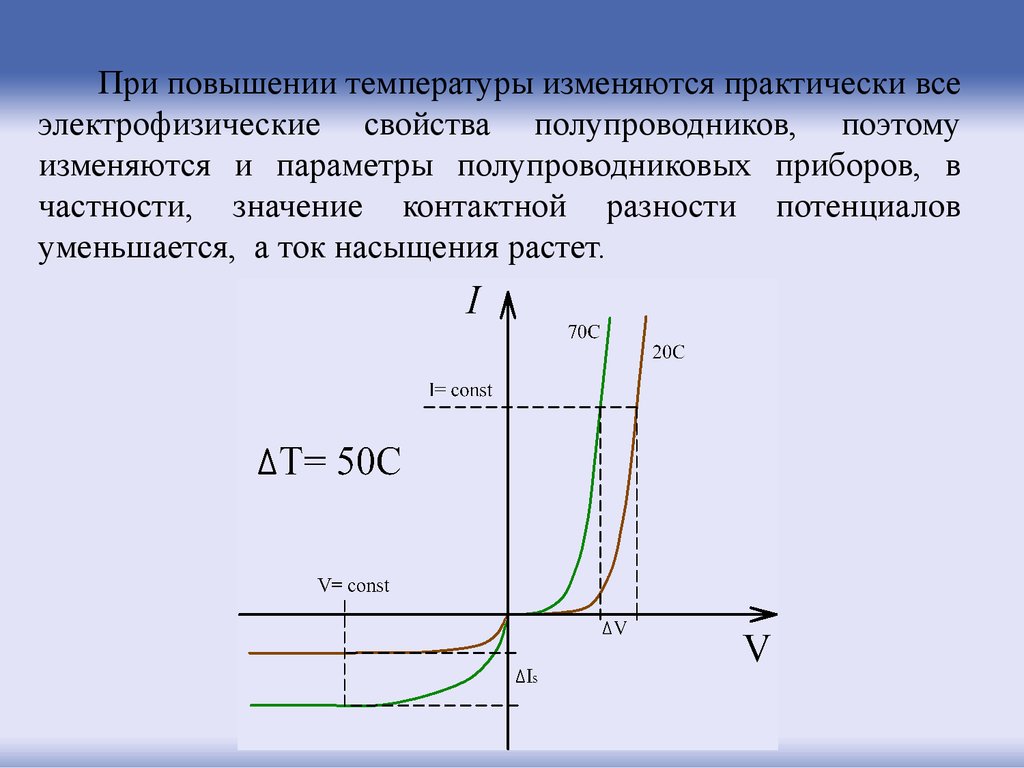
62.
При повышении температуры изменяются практически всеэлектрофизические свойства полупроводников, поэтому
изменяются и параметры полупроводниковых приборов, в
частности, значение контактной разности потенциалов
уменьшается, а ток насыщения растет.
63.
Изменение температуры диода может произойти не тольковследствие изменения температуры окружающей среды, но и за
счет саморазогрева pn-перехода при больших плотностях
протекающего через него токов.
Ge
Si
64.
Снижение влияния температуры добиваются путемвведения специальных конструктивных элементов корпусов –
радиаторов
65.
66. Стабилитроны
Стабилитрон (опорный диод) – полупроводниковыйдиод, предназначенный для стабилизации напряжения.
Стабилитроны используют также в качестве
ограничителей постоянного или импульсного напряжения,
элементов межкаскадной связи, источников эталонного
напряжения и др.
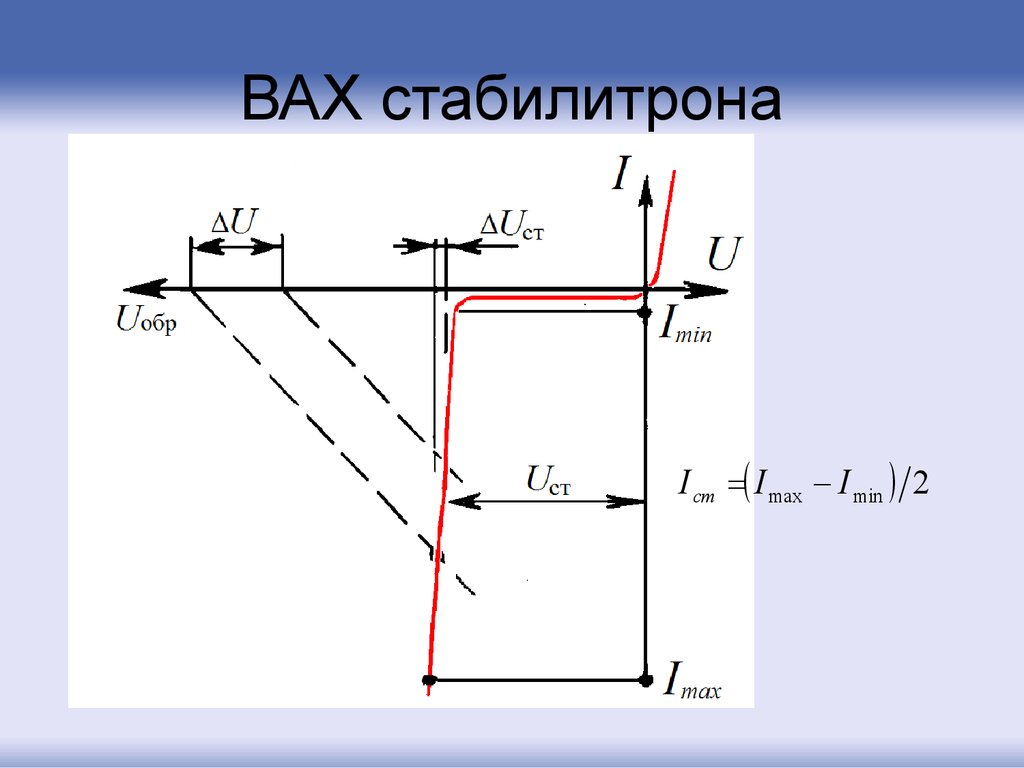
67. ВАХ стабилитрона
I ст I max I min 268.
Основными характеристиками стабилитрона являются токIст и напряжение Uст стабилизации, дифференциальное
напряжение стабилитрона rд и температурная зависимость этих
параметров.
Основное назначение стабилитрона – стабилизация
напряжения на нагрузке (Rн), при изменяющемся напряжении во
внешней цепи. В неразветвленную часть цепи включают
балластный резистор R0, сопротивление которого должно быть
существенно больше дифференциального сопротивления
стабилитрона .
69.
U н U стI Б I н I ст
U I н Rн I Б RБ U ст I Б RБ
U U ст U ст
I ст
RБ
Rн
U ст
RБ
U I ст RБ / 1
Rн
1
1
RБ I ст RБ
U U ст
Rн RБ
70.
В режиме короткого замыкания (U ст 0)I ст I КЗ
U ст U ХХ
Un
RБ
U n. Rн
Rн RБ
Нестабильность выходного напряжения вызывается двумя
основными
причинами:
нестабильностью
входного
напряжения U п и
нестабильностью
входного
тока
(нестабильностью сопротивления нагрузки Rн).
71.
U U ст RБ I н I стU ст U ст
U ст RБ
rd
Rн
U ст
U
1 RБ Rн RБ rd
72. Туннельные диоды
Туннельный диод был предложен в 1958 году ЛеоИсаки, который в 1973 году получил Нобелевскую премию
по физике за открытие эффекта туннелирования
электронов, применяемого в этих диодах.
Туннельным диодом называют полупроводниковый
диод на основе p+n+-перехода с сильнолегированными
областями, на прямом участке ВАХ которого наблюдается
N-образная зависимость тока от напряжения.
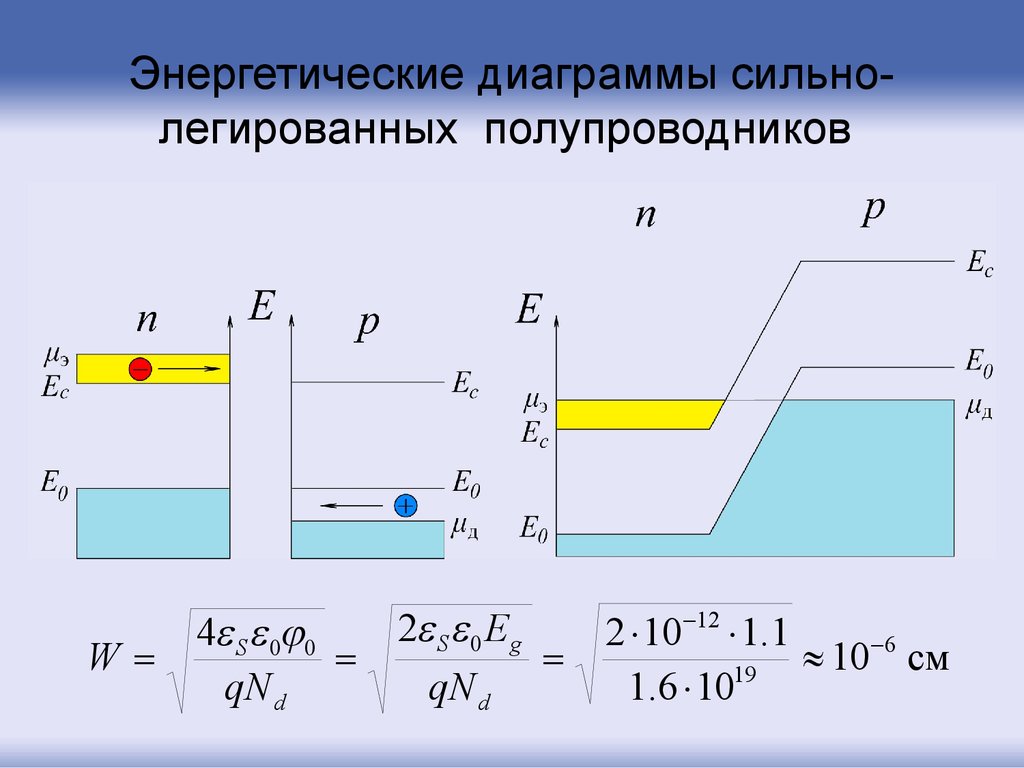
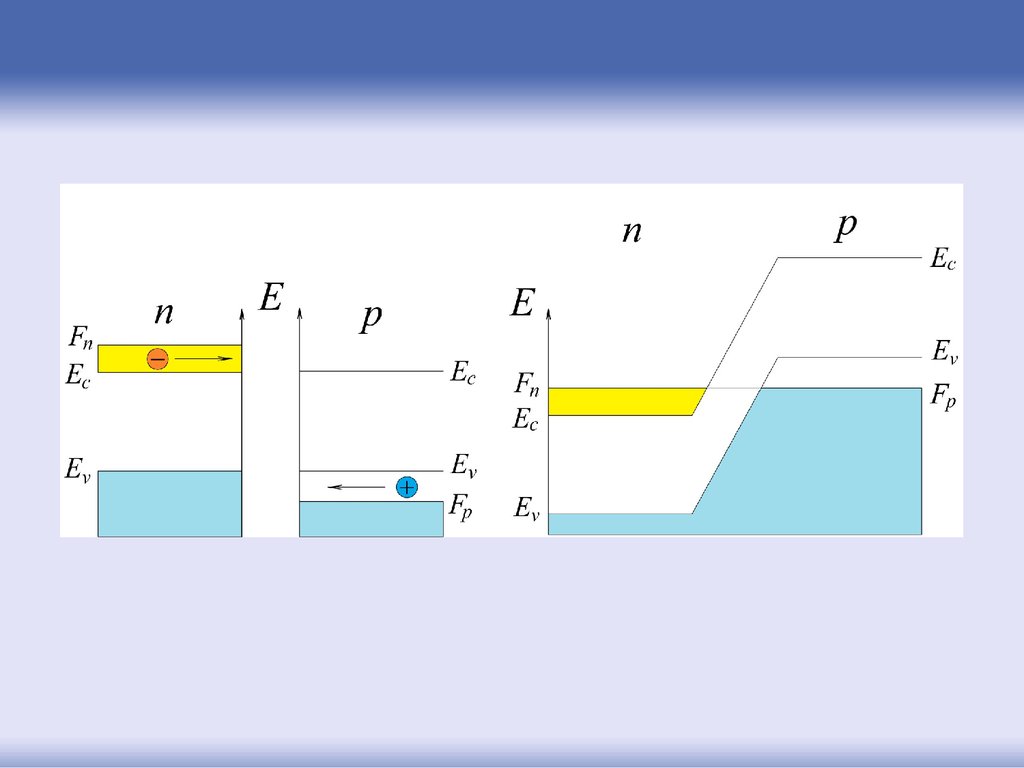
73.
Энергетические диаграммы сильнолегированных полупроводниковW
4 S 0 0
qN d
2 S 0 Eg
qN d
2 10 12 1.1
6
10
см
19
1.6 10
74.
k2
2
E kT
; k
; E
kT
2
2m
2m
2
2
2
2
h2
λ
2m kT
6.63 10
34 2
2 9.1 10
31
1.38 10
23
300
76
75.
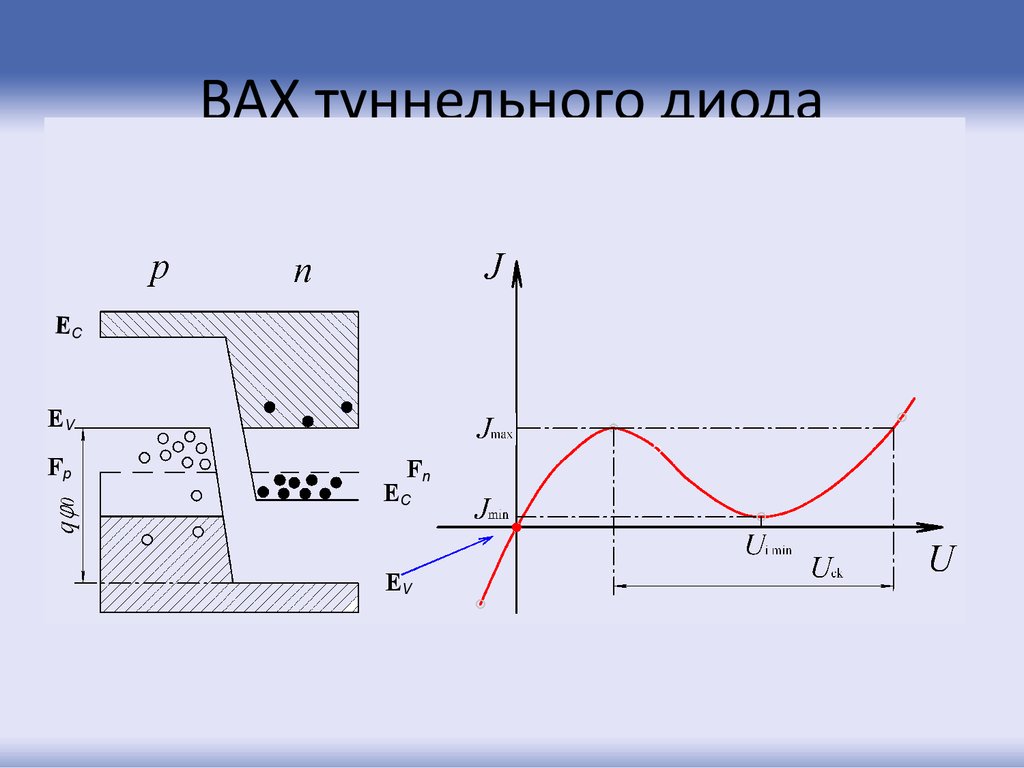
76. ВАХ туннельного диода
ECEV
Fp
Fn
EC
EV
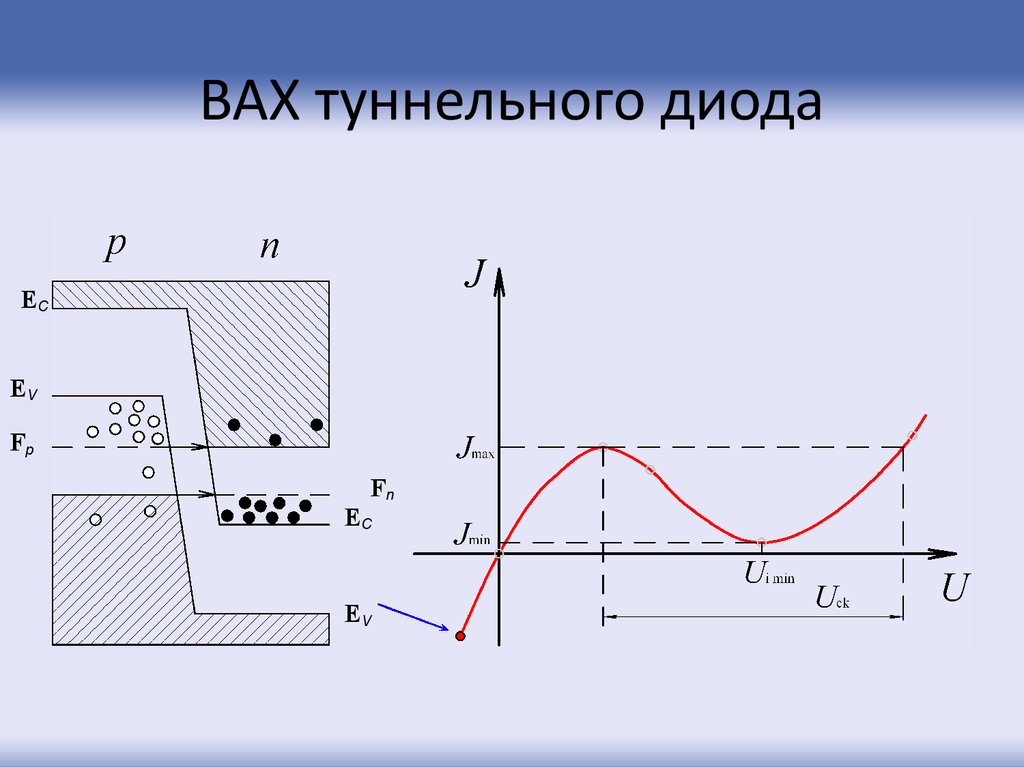
77. ВАХ туннельного диода
ECEV
Fp
Fn
EC
EV
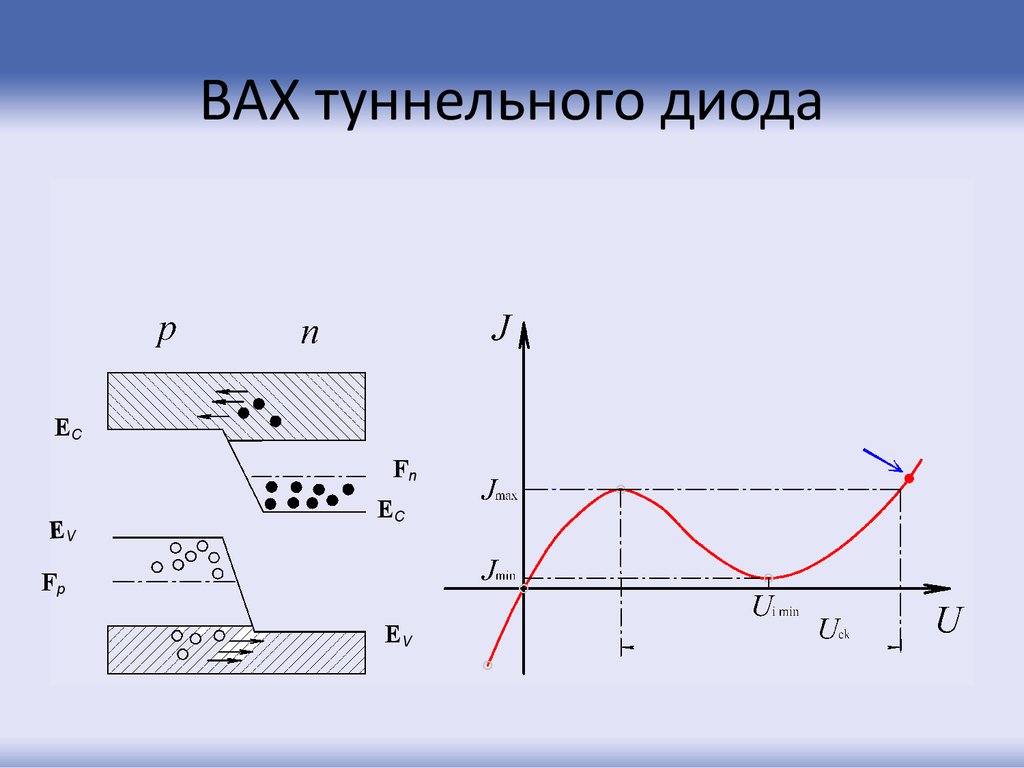
78. ВАХ туннельного диода
ECEV
Fp
Fn
EC
EV
79. ВАХ туннельного диода
ECFn
EV
EC
Fp
EV
80. ВАХ туннельного диода
ECFn
EV
EC
Fp
EV
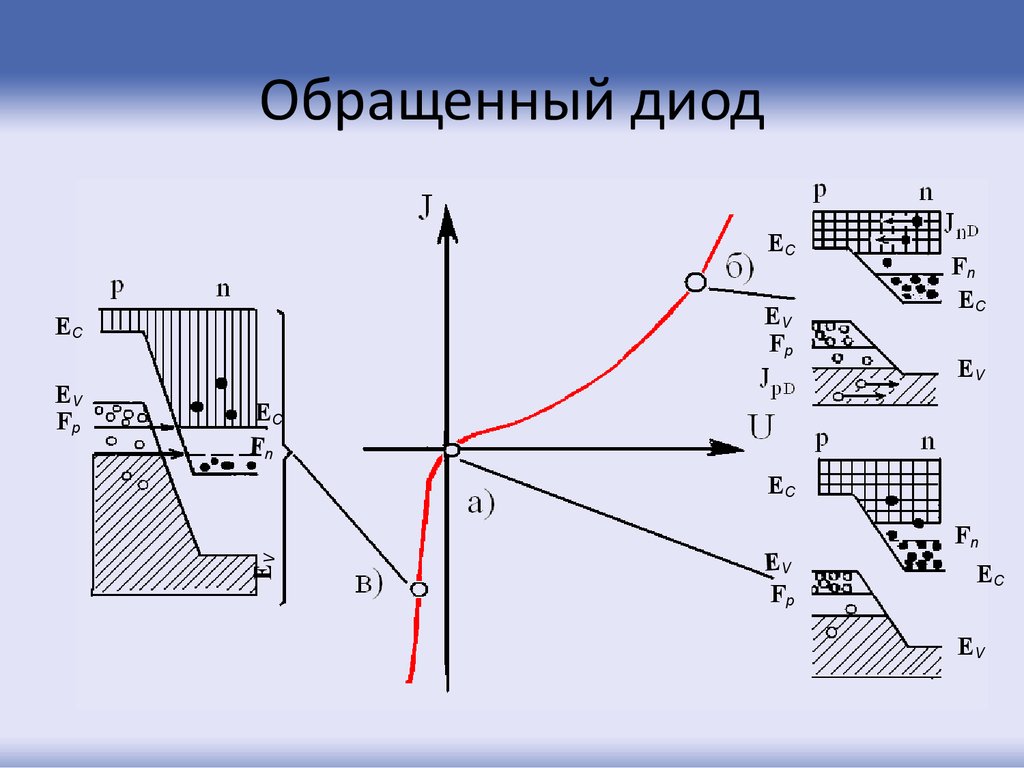
81. Обращенный диод
ECEV
Fp
EC
EV
EC
Fn
EC
EV
EV
Fp
Fn
EC
EV
Fp
Fn
EC
EV
82. Расчет ВАХ барьера Шоттки
83. Расчет ВАХ барьера Шоттки
При приложении напряжения:2 0 k Vсм
W
q Nd
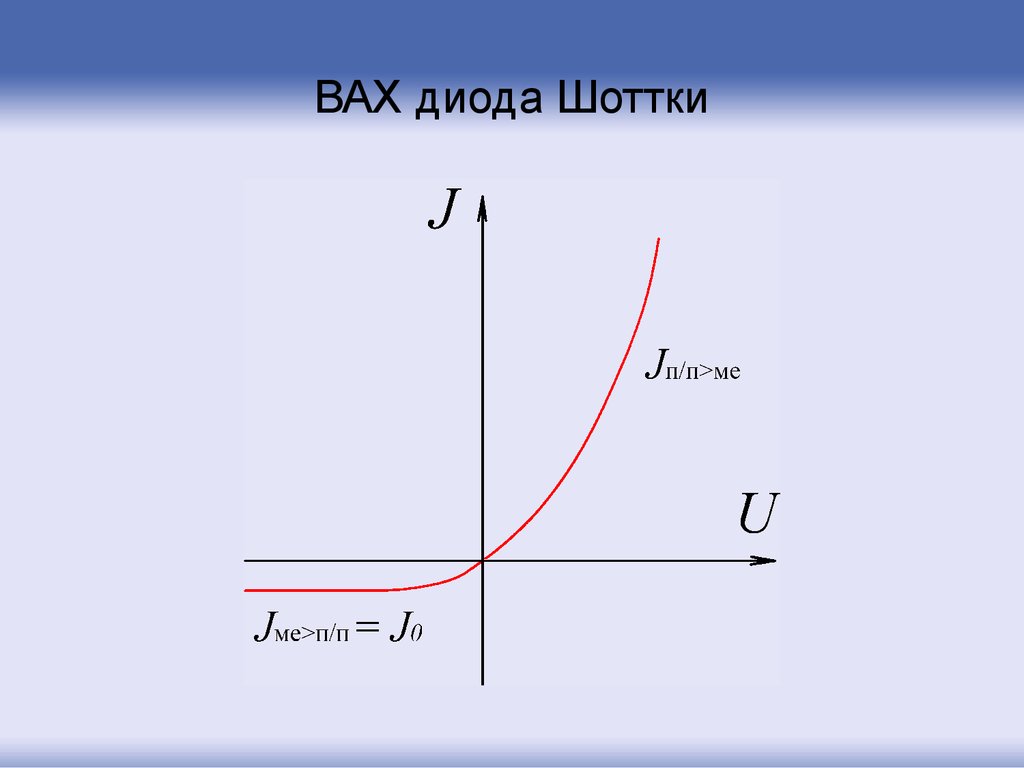
J J п.п
где
Js A T 2 e
4 mn* q k 2
mn*
A
120
3
h
m0
V
T
Jм Js e
1
Ub
T
А
см 2 K 2 - Постоянная Ричардсона
84. ВАХ диода Шоттки
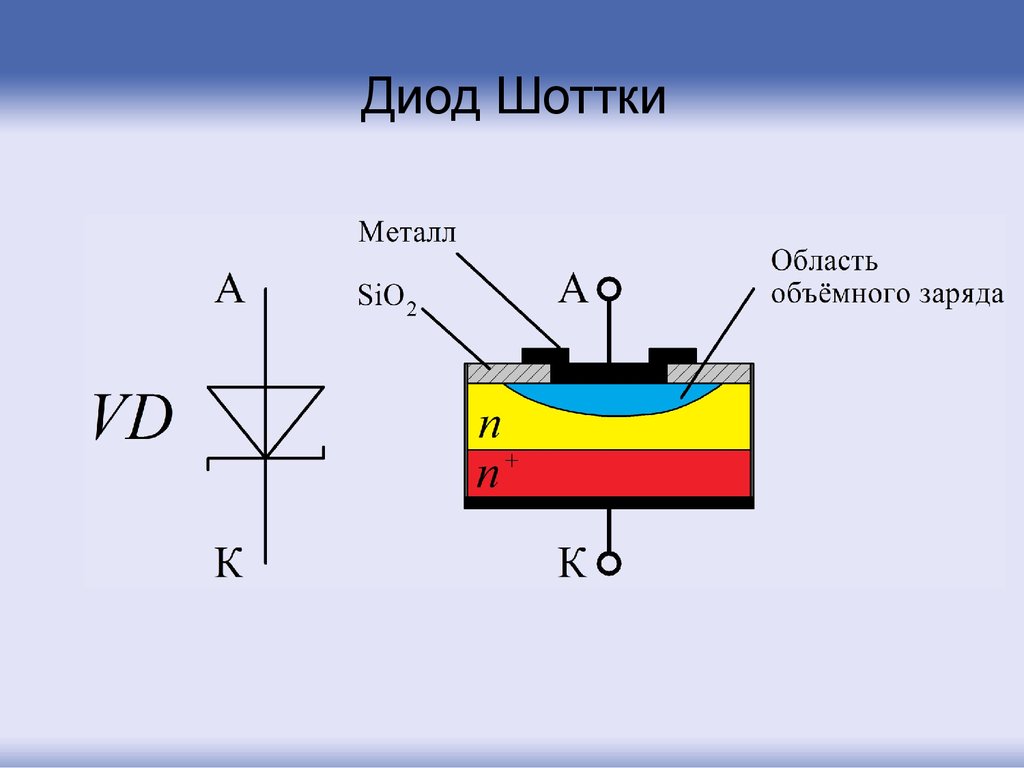
85. Диод Шоттки
86.
•Диоды Шоттки характеризуются быстройрекомбинацией инжектированных носителей
(время жизни носителей крайне мало), а значит и
высоким быстродействием.
• Благодаря минимальному сопротивлению
базы и отсутствию процессов накопления и
рассасывания избыточных зарядов, быстродействие получается достаточно высоким:
граничная частота
.
10
f гр 10 Гц
























































 Электроника
Электроника








