Арифметическая и геометрическая прогрессии

1.

2. Прогрессии

Арифметическая прогрессия
Последовательность в
которой каждый член
начиная со второго равен
предыдущему,
сложенному с одним и
тем же числом.
Число d - разность прогрессии
d = a2-a1 = a3-a2 = a4-a3 =….
Геометрическая прогрессия
Последовательность
отличных от нуля чисел
в которой каждый член
начиная со второго
равен предыдущему
умноженному на одно и
тоже число.
Число q - знаменатель прогрессии.
q = b2:b1 = b3:b2 = b4:b3 =…

3. Формула n-го члена прогрессии

арифметической,
an=a1+d(n-1)
Дано: a1 = 7, d = 5
Найти: a4,.
a4=22
геометрической
n-1
bn=b1q
Дано: b1 = 3, q = 2
Найти: b3.
b3=12

4. Характеристическое свойство прогрессий

Каждый член
последовательности начиная
со второго есть среднее
арифметическое между
предыдущим и последующим
членами прогрессии
an 1 an 1
an
2
х1, х2, 4, х4,14, …
найти: х4
Х4=9
Каждый член
последовательности начиная
со второго есть среднее
геометрическое между
предыдущим и последующим
членами последовательности
(bn >0)
bn bn 1 bn 1
b1, b2, 1, b4, 16, …- все члены
положительные числа
найти: b4
b4=4

5. Формулы суммы n-первых членов прогрессий

арифметическая
геометрическая
a1 an
Sn
n
2
b1 (1 q n )
Sn
,q 1
1 q
2a1 d (n 1)
Sn
n
2
Дано:
4
a1 = 5, d =
Найти: S5
S5 = 65
b1 qbn
Sn
,q 1
1 q
Дано: b
1
= 2, q = - 3
Найти: S4
S4 = - 40

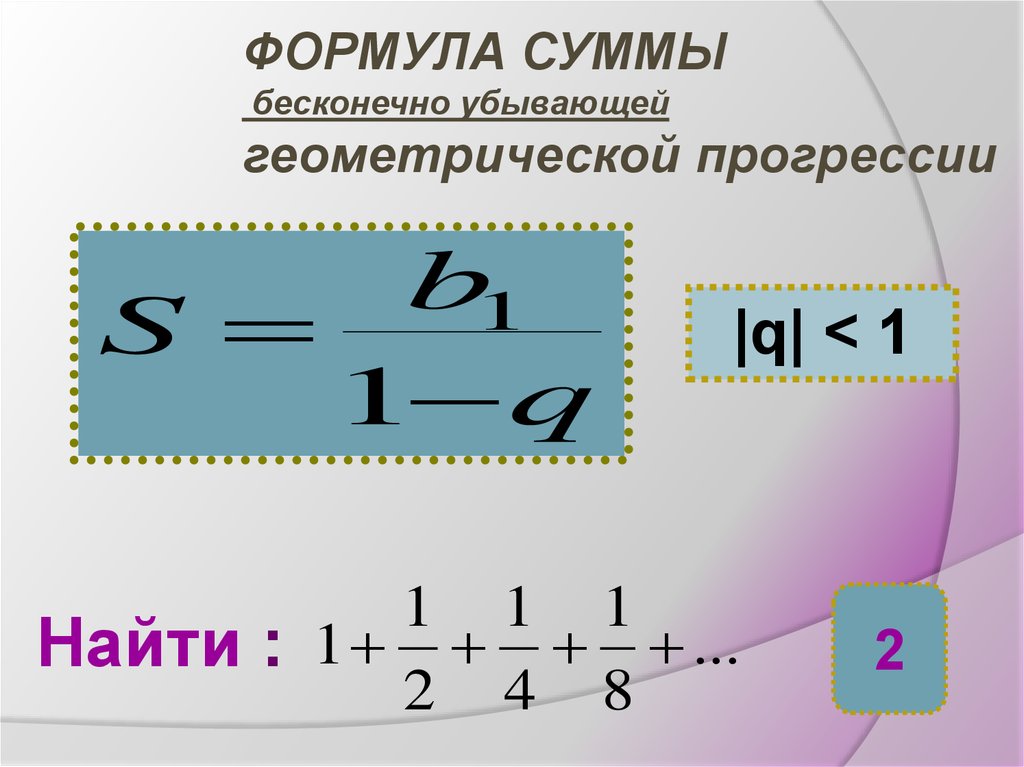
6. ФОРМУЛА СУММЫ бесконечно убывающей геометрической прогрессии

b1
S
1 q
|q| < 1
1 1 1
Найти : 1 ...
2 4 8
2

7.

Самостоятельная работа ( тест)
Часть I ( 0,5 балла )
1. Про арифметическую прогрессию (аn)
известно, что а7 = 8, а8 = 12. найдите
разность арифметической прогрессии.
А) -4
Б) 4
В) 20
Г) 3
2. Геометрическая прогрессия задана
формулой b 32 n .
n
Найдите знаменатель геометрической прогрессии.
А) -3
Б) 18
В) 3
Г) 9
3. Найдите сумму семи первых членов геометрической прогрессии 4; 8; …
А) - 254
Б) 508
В) 608
Г) - 508

8.

4. Последовательность аn задана формулойаn n 2 2n 1.
Найдите номер члена последовательности, равного 7.
А) 4
Б) - 2
В) 2
Г) - 4
Часть II (задания на 2 балла)
5. В геометрической прогрессии (bn) b1 = 8, b3 = 24. Ответ:
Найдите b5. ( для q > 0 )
b5 = 72
(задания на 3 балла)
6. Сумма второго и пятого членов арифметической
прогрессии равна 11. Третий её член на 6 больше первого.
Ответ:
Найдите второй и четвёртый члены.
а2 =1; а4 = 7,
Количество набранных баллов
оценка
1,5 - 2
«3»
2,5 – 4,5
«4»
5 – 7,5
«5»

9.

В сборнике по подготовке к
экзамену-240 задач. Ученик
планирует начать их решение 2
мая, а закончить 16 мая, решая
каждый день на две задачи
больше, чем в предыдущий
день. Сколько задач ученик
запланировал решить 12 мая?
В
амфитеатре
расположены 10 рядов,
причем в каждом
следующем ряду на 20
мест больше чем в
предыдущем, а в
последнем ряду 280
мест. Сколько человек
вмещает амфитеатр?

10.

- Решение:
280= а + 20∙(10-1);
а = 280 - 20 ∙ 9 = 100;
S = ½(100+280) ∙ 10 =1900.
Ответ:1900 человек
вмещает амфитеатр.
1
1
10
- Решение:
240=½(2 а1 +2 ∙14) ∙ 15;
240:15= а₁ + 14;
а₁ = 2;
а₁₁ = 2+2 ∙ 10 = 22.
Ответ:22 задачи надо решить
12 мая.

11.

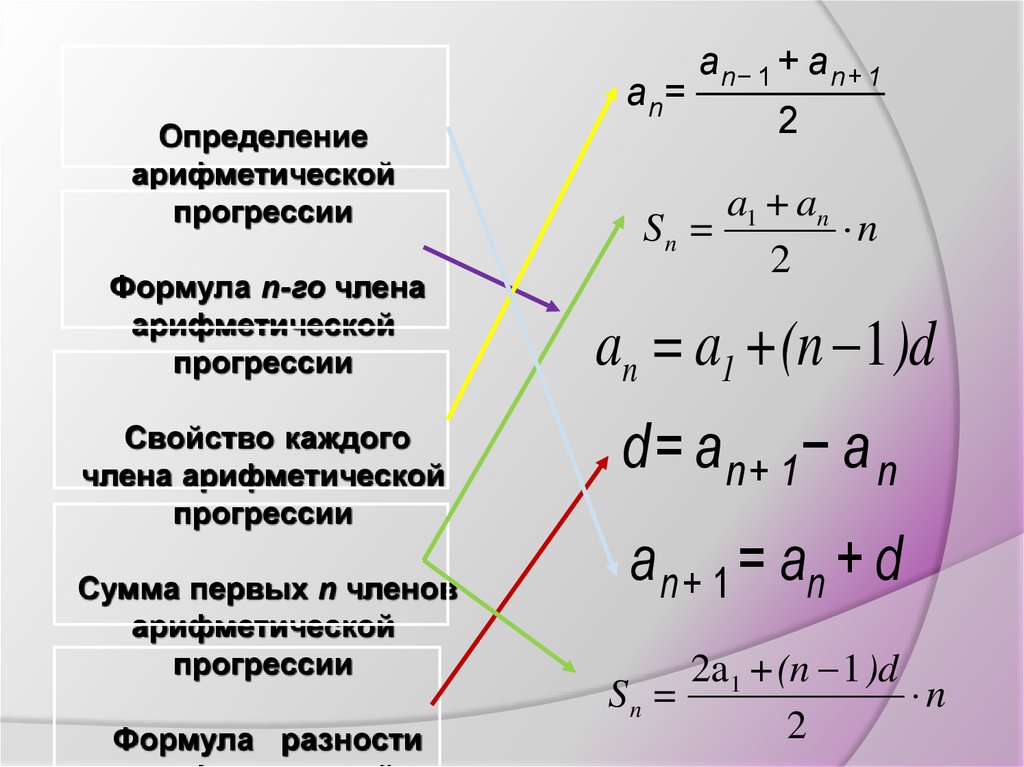
Определение
арифметической
прогрессии
Формула n-го члена
арифметической
прогрессии
Свойство каждого
члена арифметической
прогрессии
Сумма первых n членов
арифметической
прогрессии
Формула разности
an=
a n− 1 + a n+ 1
2
a1 + an
Sn =
n
2
an = a1 +(n 1 )d
d= a n+ 1 − a n
a n+ 1 = an + d
2a1 + (n 1 )d
Sn =
n
2