Похожие презентации:
Арифметическая и геометрическая прогрессии
1.
2.
ПрогрессииАРИФМЕТИЧЕСКАЯ
ПРОГРЕССИЯ
ГЕОМЕТРИЧЕСКАЯ
ПРОГРЕССИЯ
2
3.
ОпределенияЧисловая
последовательность а1, а2,
а3, …,аn, … называется
арифметической
прогрессией, если для всех
натуральных n выполняется
равенство an+1 = an + d, где d
– некоторое число.
Числовая
последовательность
b1, b2, b3, …, bn, … называется
геометрической
прогрессией, если для всех
натуральных n
выполняется равенство
bn+1 = bnq, где bn≠0, q –
некоторое число, не
равное нулю.
прогрессии
3
4.
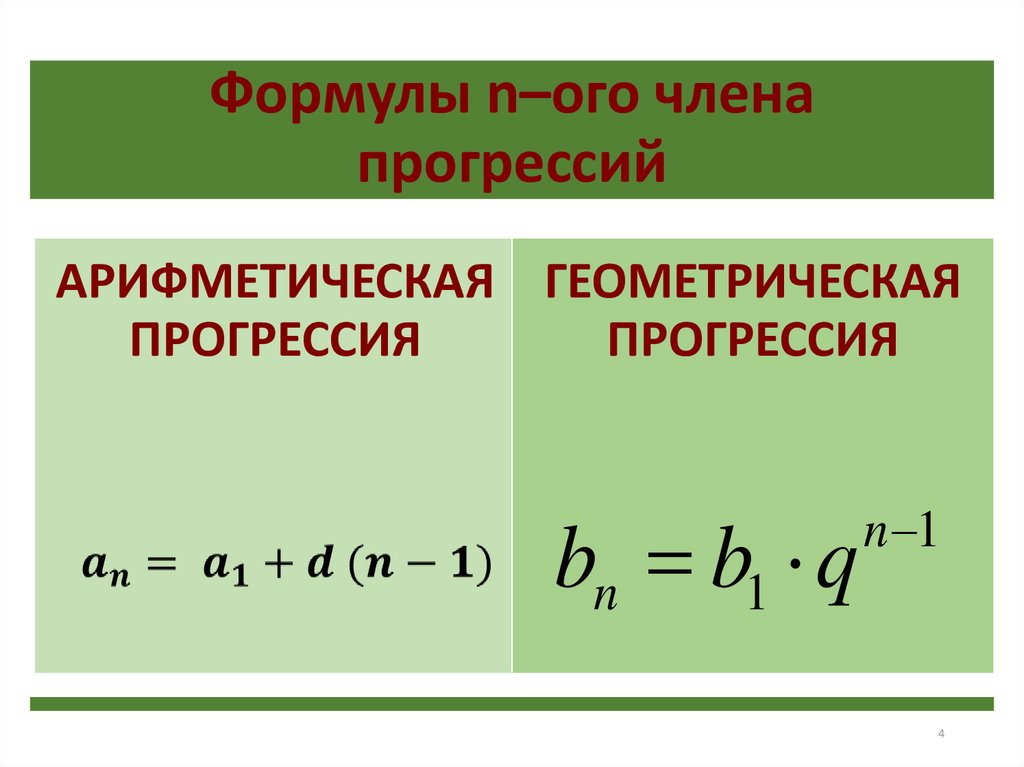
Формулы n–ого членапрогрессий
АРИФМЕТИЧЕСКАЯ ГЕОМЕТРИЧЕСКАЯ
ПРОГРЕССИЯ
ПРОГРЕССИЯ
bn b1 q
n 1
4
5. Формулы суммы n первых членов прогрессий
арифметическаягеометрическая
a1 an
Sn
n
2
b1 (1 q n )
Sn
,q 1
1 q
2a1 d (n 1)
Sn
n
2
Дано:
a1 = 5, d = 4
Найти: S5
S5 = 65
b1 qbn
Sn
,q 1
1 q
Дано: b
1
= 2, q = - 3
Найти: S4
S4 = - 40
6.
1) Дано: (а n ) арифметическая прогрессияа1 = 5 d = 3
Найти: а6 ; а10.
Решение: используя формулу
а n = а 1+( n -1) d
а6 = а1 +5 d = 5+ 5 . 3 = 20
а10 = а1 +9 d = 5+ 9 . 3 = 32
Ответ: 20; 32
Решение
7.
2) Дано: (b n ) геометрическаяпрогрессия
b1= 5 q = 3
Найти: b3 ; b5.
Решение: используя формулу b
n = b1 q n-1
b3 =b1q2 = 5 . 32 =5 . 9=45
b5 =b1q4 = 5 . 34 =5 . 81=405
Ответ:45; 405.
Решение
8.
3) Дано: (а n ) арифметическаяпрогрессия
а4 = 11 d = 2
Найти: а1 .
Решение: используя формулу
а n= а 1+ ( n – 1) d
а4 = а1 +3 d ; а1= а4 – 3 d =11 – 3 . 2
=5
Ответ: 5.
Решение
9.
Дано: (b n ) геометрическаяпрогрессия
b4= 40 q = 2
Найти: b1.
Решение:
используя
формулу
b
n
=
b
q
1
n-1
4)
b4 =b1q3 ; b1 = b4 : q3 =40:23 =40 :8=5
Ответ: 5.
Решение
10.
В благоприятных условиях бактерии размножаются так, что напротяжении одной минуты одна из них делится на две. Указать
количество бактерий, рождённых одной бактерией за 7 минут.
11.
Данная последовательность - геометрическаяпрогрессия со знаменателем q 2 n 7 b1
b1q b1
Sn
q 1
1
n
Зная формулу
1 27 1
S7
127
2 1
Получаем
12.
Амфитеатр состоит из 10 рядов, причем в каждомследующем ряду на 20 мест больше, чем в предыдущем, а в
последнем ряду 280 мест. Сколько человек вмещает
амфитеатр?
13.
Итак, перед нами арифметическая прогрессия.Пусть х мест в первом ряду, (х+20) мест во втором ряду, (х+20+20),
т. е. (х+40) мест в третьем ряду и т. д.
a1 x a2 x 20
аn а1 d (n 1)
a10 a1 9d
d 20
a10 280
280 x 9 20
x 100
Значит, 100 мест в первом ряду
Sn
а1 аn
n
2
S10
а1 а10
10
2
S10
100 280
10
2
Ответ:1900
S10 1900
14.
Задача: Вертикальные стержни фермы имеют следующуюдлину: наименьший 5 дм, а каждый следующий - на 2 дм
длиннее. Найдите длину семи таких стержней.
Решение: Перед нами арифметическая
прогрессия
5, 7, 9, 11, ….
a1 5
d 2
а1 аn
Sn
n
2
аn а1 d (n 1)
S7
5 17
7
2
Ответ: 77 дм
n 7
а1 а7
S7
7
2
а7 а1 d (7 1)
а7 17
15. Домашнее задание
• Параграф 38, выучить формулы арифметической игеометрической прогрессии;
• Упражнения 38.22 – 38.34 (все номера под буквой «б»)












 Математика
Математика








