Похожие презентации:
Окружность. Теоремы
1.
ВВЫПОЛНИЛИ:
Матвеева Н., Давлетшина Э.,
Полякова Ж., Санникова К.,
Соловьева Ж., Поспелов И.,
Сычев Г., Мерзляков В.
2.
ОКРУЖНОСТЬ —замкнутая плоскаякривая, все точки которой одинаково
удалены от ее центра O
3.
Радиус —отрезок, соединяющий центр окружности содной из её точек.
Хорда-отрезок, соединяющий две точки
окружности.
Диаметр- хорда проходящая через центр
окружности,
Дуга окружности- любые две несовпадающие точки
окружности делящие её на две части
Дуга называется полуокружностью, если отрезок,
соединяющий её концы, является диаметром.
Дуга окружности- прямая, имеющая с окружностью
ровно одну общую точку, а их общая точка
называется точкой касания прямой и окружности.
4.
Если расстояние от центра окружности допрямой меньше радиуса окружности (d<r), то
прямая и окружность имеют две общие точки. В
этом случае прямая называется секущей.
5.
Если расстояние от центра окружности допрямой равно радиусу окружности (d=r), то
прямая и окружность имеют только одну
общую точку
6.
Если расстояние от центра окружности допрямой больше радиуса окружности(d>r),
то прямая и окружность не имеют общих
точек
7.
Теорема:Касательная к окружности перпендикулярна к радиусу,
точку касания.
проведенному в
8.
Если прямая проходит через конец радиуса, лежащий на окружности, иперпендикулярна к этому радиусу, то она является касательной
.
9.
Вписанный угол- угол, вершина котороголежит на окружности.
10.
Вписанный угол измеряется половинойдуги, на которую он опирается.
11.
Луч ВО делит угол АВС на два угла. В этом случае луч ВО пересекает дугу АС в точке D. Точка Dразделяет дугу АС на две дуги: AD и DC.
Из доказанного в п1:
12.
Вписанные углы , опирающиеся на одну иту же дугу , равны
13.
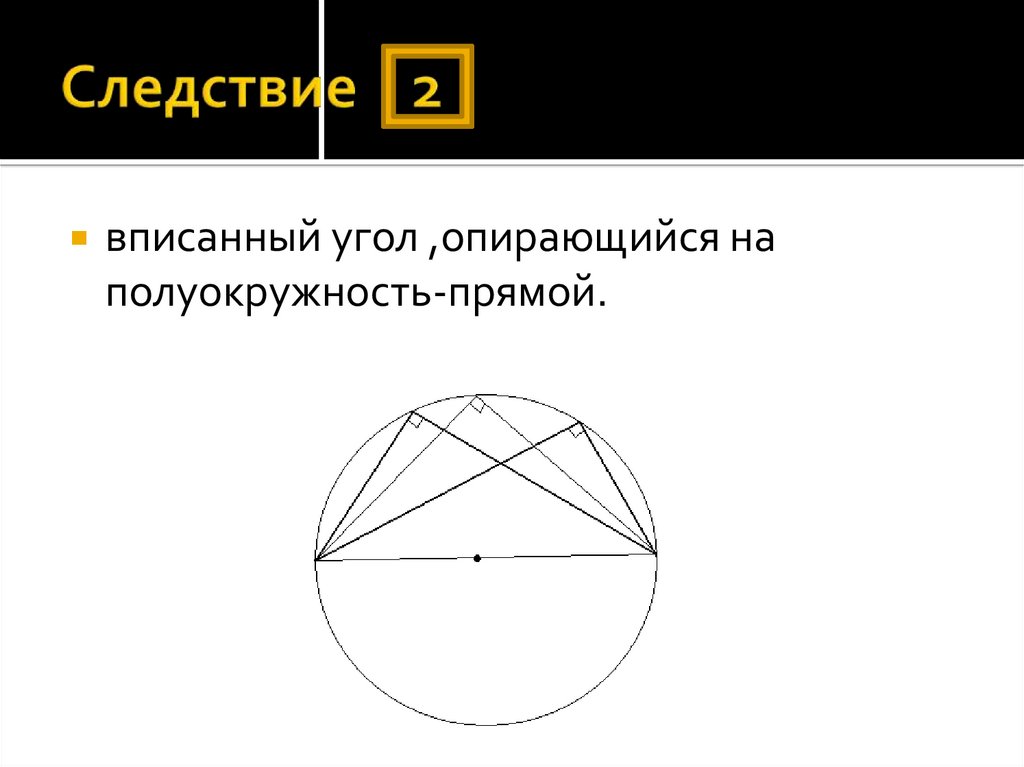
вписанный угол ,опирающийся наполуокружность-прямой.
14.
Если две хорды окружности пересекаются , то произведениеотрезков одной хорды равно произведению отрезков другой
хорды.














 Математика
Математика