Vienkāršās formas

1. Vienkāršās formas

2. Kubiskā singonija

Nav vienreizējo virzienu telpā
Visas formas ir slēgtas
Nepāriet neviena forma no citām singonijām
Kopā 15 vienkāršās formas

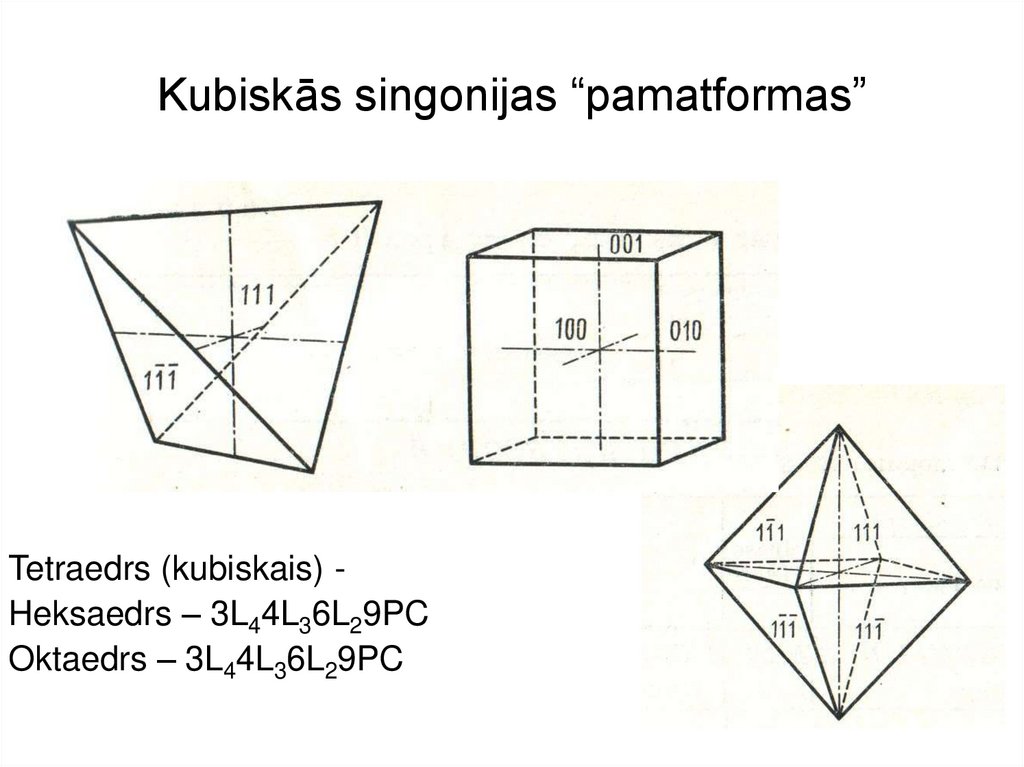
3. Kubiskās singonijas “pamatformas”

Tetraedrs (kubiskais) Heksaedrs – 3L44L36L29PC
Oktaedrs – 3L44L36L29PC

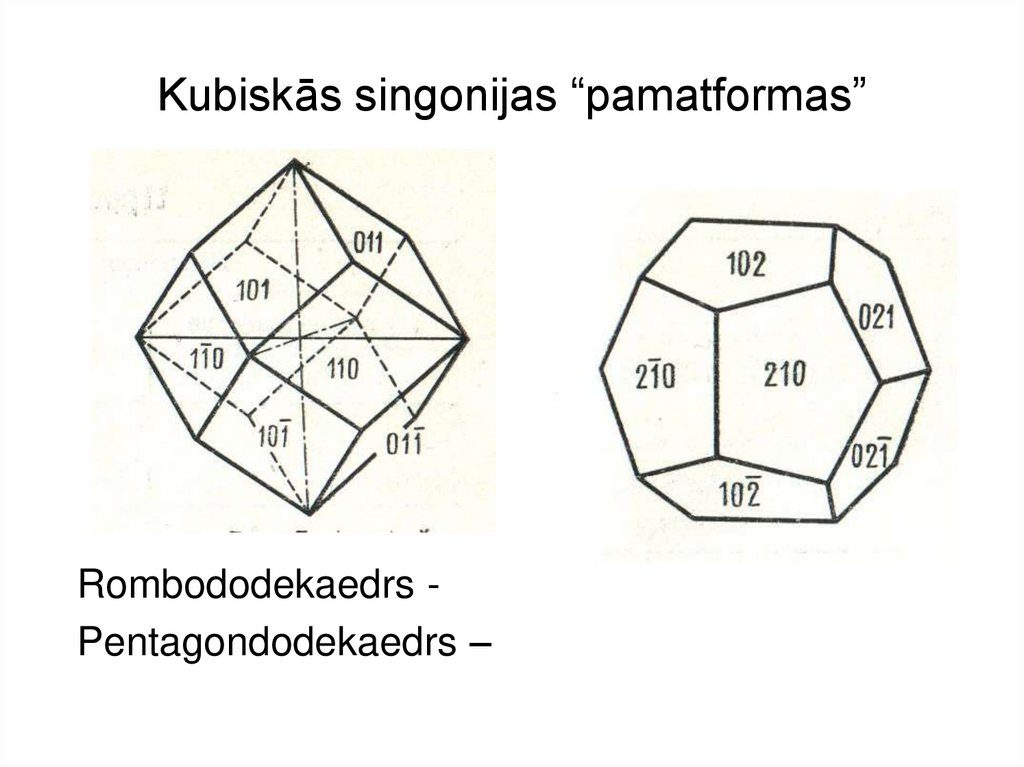
4. Kubiskās singonijas “pamatformas”

Rombododekaedrs Pentagondodekaedrs –

5. No “pamatformām” “izveidotās” formas

Jaunu formu izveidošanas principi:
daudzkāršo skaldņu skaitu
daudzkāršot var dažādi
daudzkāršotajai skaldnei var būt dažādas formas
Jaunās formas nosaukums ietver:
jaunās skaldnes formu
vecās skaldnes daudzkāršojumu
pamatformas nosaukumu

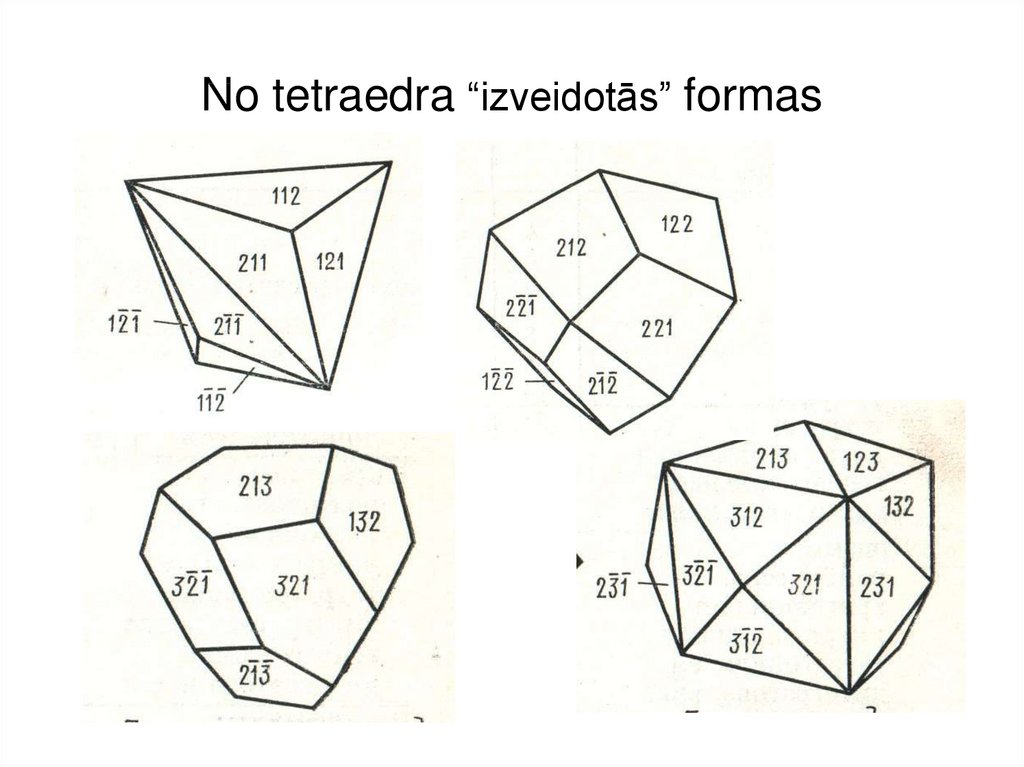
6. No tetraedra “izveidotās” formas

Trigontritetraedrs – 12 skaldnes
Tetragontritetraedrs – 12 skaldnes
Pentagontritetraedrs – 12 skaldnes (enantiomēri)
Heksatetraedrs – 24 skaldnes

7. No tetraedra “izveidotās” formas

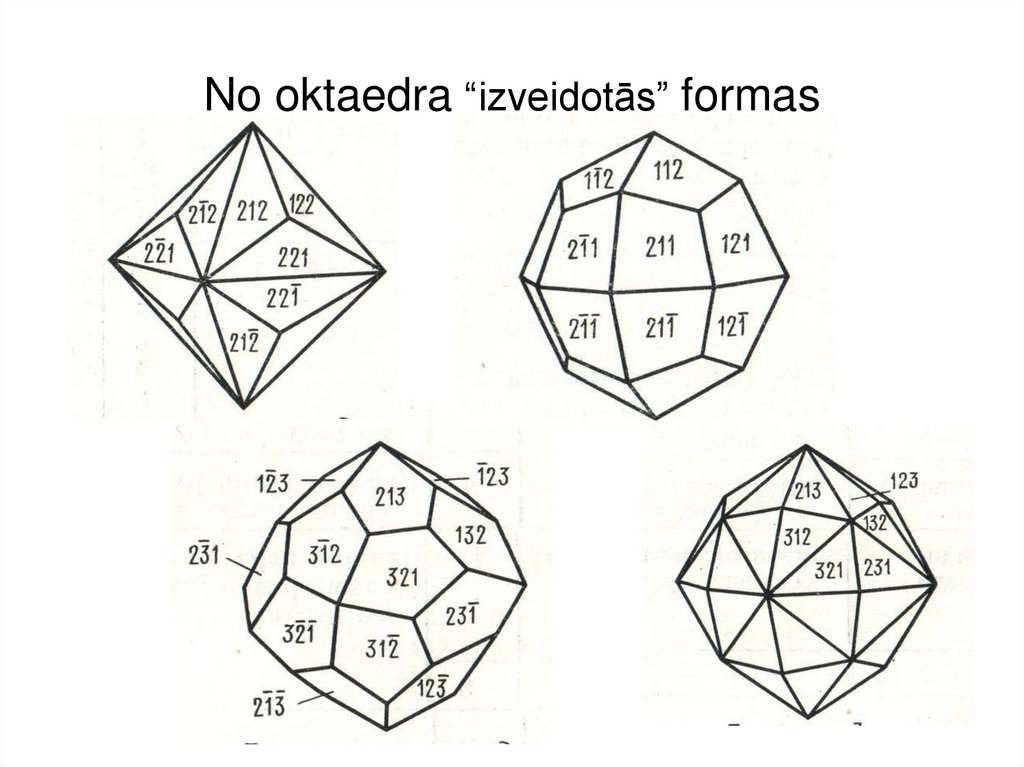
8. No oktaedra “izveidotās” formas

Trigontrioktaedrs – 24 skaldnes
Tetragontrioktaedrs – 24 skaldnes
Pentagontrioktaedrs – 24 skaldnes (enantiomēri)
Heksaoktaaedrs – 48 skaldnes

9. No oktaedra “izveidotās” formas

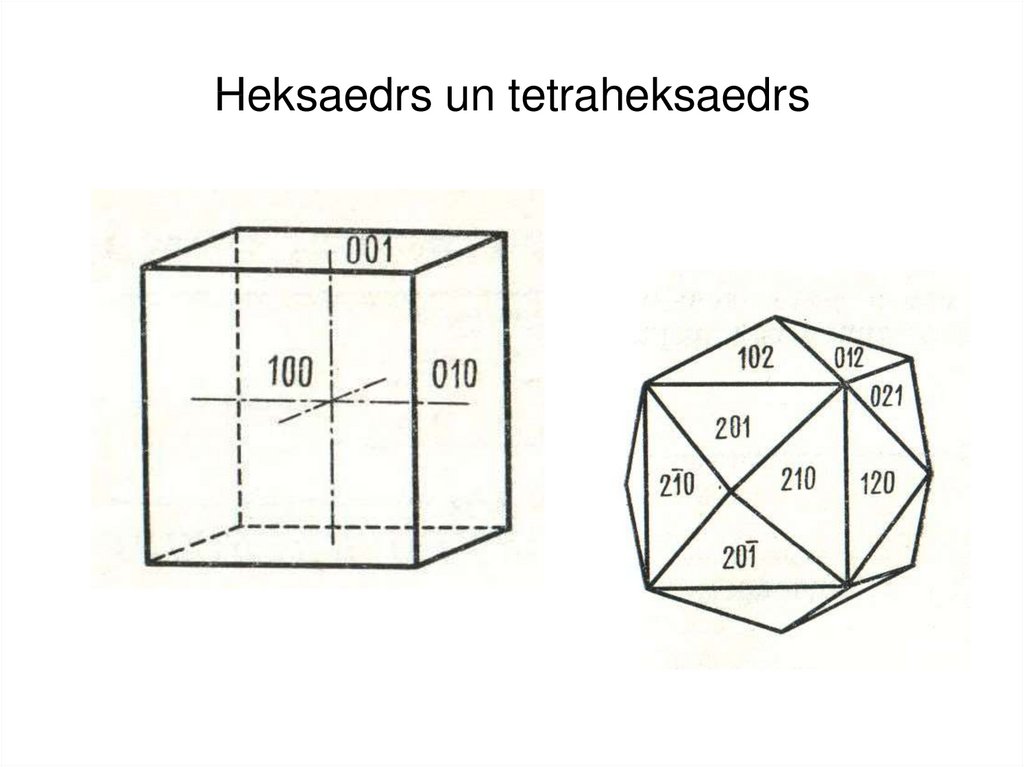
10. No heksaedra “izveidotā” forma

Tetraheksaedrs – 24 skaldnes

11. Heksaedrs un tetraheksaedrs

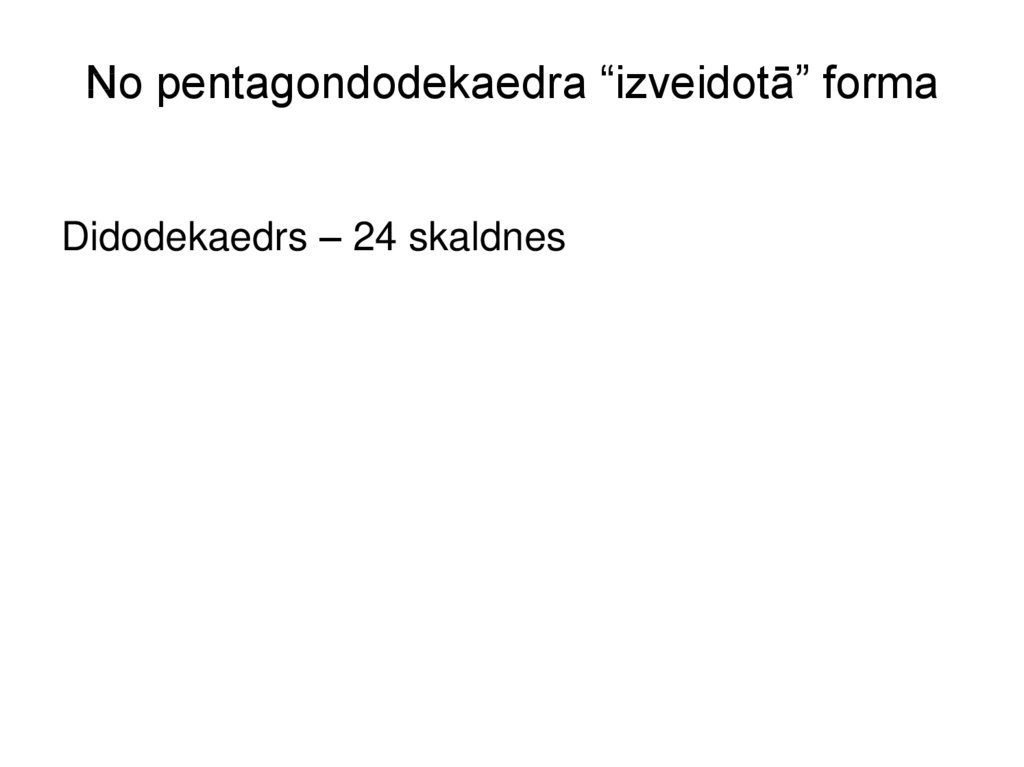
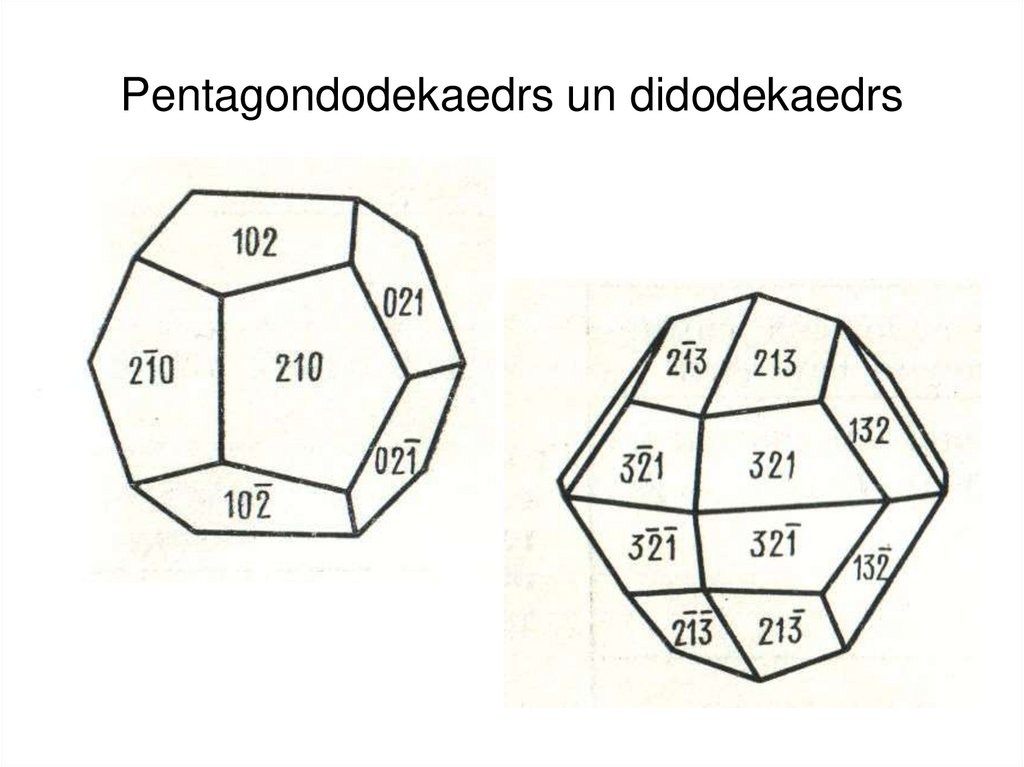
12. No pentagondodekaedra “izveidotā” forma

Didodekaedrs – 24 skaldnes

13. Pentagondodekaedrs un didodekaedrs

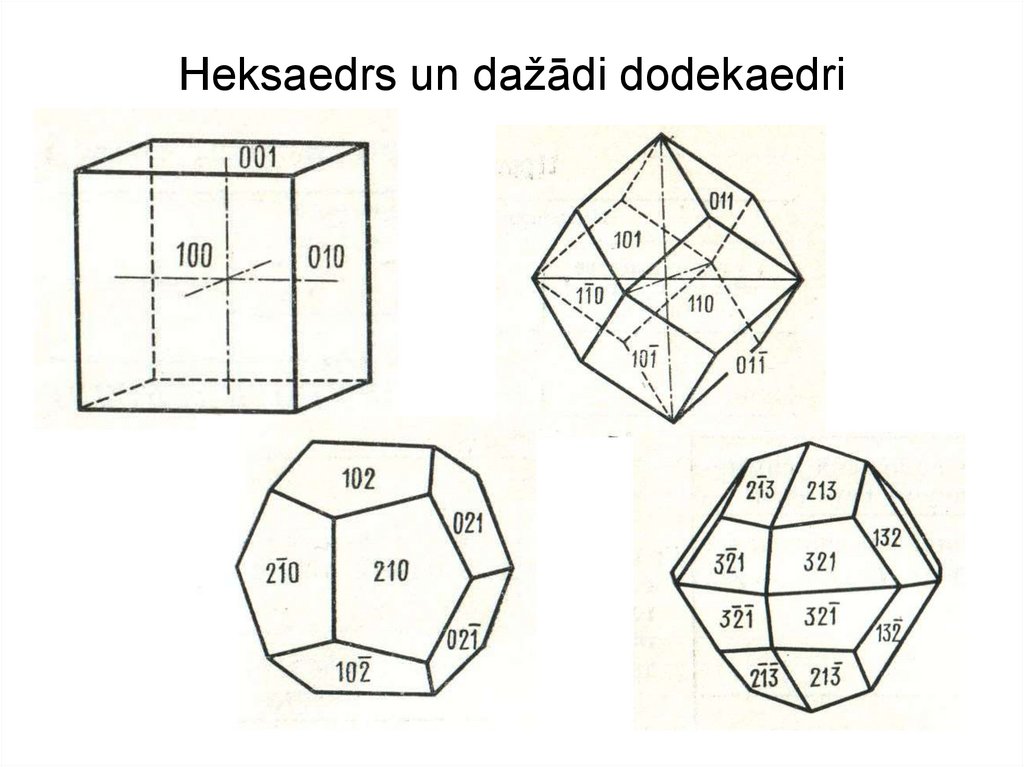
14. Heksaedrs un dažādi dodekaedri

15. Vienkāršo formu sadalījums pa simetrijas klasēm

28.
4L33L2
Heksaedrs
Rombododekaedrs
Pentagondodekaedrs
Tetraedrs
Trigontritetraedrs
Tetragontritetraedrs
Pentagontritetraedrs
1
1
D
2
D
D
D

16. Vienkāršo formu sadalījums pa simetrijas klasēm

29.
3L24L33PC Heksaedrs
Rombododekaedrs
Pentagondodekaedrs
Oktaedrs
Tetragontrioktaedrs
Trigontrioktaedrs
Didodekaedrs
1
1
D
1
D
D
D

17. Vienkāršo formu sadalījums pa simetrijas klasēm

30.
3Li44L36P
(3L24L36P)
Heksaedrs
Rombododekaedrs
Tetraheksaedrs
Tetraedrs
Trigontritetraedrs
Teragontritetraedrs
Heksatetraedrs
1
1
D
2
D
D
D

18. Vienkāršo formu sadalījums pa simetrijas klasēm

31.
3L44L36L2
Heksaedrs
Rombododekaedrs
Tetraheksaedrs
Oktaedrs
Tetragontrioktaedrs
Trigontrioktaedrs
Pentagontrioktaedrs
1
1
D
1
D
D
D

19. Vienkāršo formu sadalījums pa simetrijas klasēm

32.
3L44L36L29PC Heksaedrs
Rombododekaedrs
Tetraheksaedrs
Oktaedrs
Tetragontrioktaedrs
Trigontrioktaedrs
Pentagontrioktaedrs
1
1
D
1
D
D
D