Vienkāršās formas

1. Vienkāršās formas

2. Kāpēc tas ir svarīgi?

Kuba simetrijas elementi:
3L44L33L29PC
Oktaedra simetrijas elementi:
3L44L33L29PC

3. Definīcija

Vienkāršā forma ir skaldņu kopums, kuras ir:
1) vienādas;
2) saistītas savā starpā ar konkrētā simetrijas
veida simetrijas elementiem
No vienas skaldnes var iegūt visās pārējās
skaldnes, kas pieder šai formai
Kā iegūt?
Iedarbojoties uz to ar konkrētā simetrijas veida
simetrijas elementiem

4. Vienkāršo formu iedalījums un raksturojums

Vispārējās formas
Īpatnējās formas
Slēgtās un vaļējās formas
Kas raksturo vienkāršo formu?
Vienādo skaldņu skaits (no 1 līdz 48)
Skaldņu savstarpējais novietojums
Vai skaldnēm ir raksturīgas formas?
Jā un nē

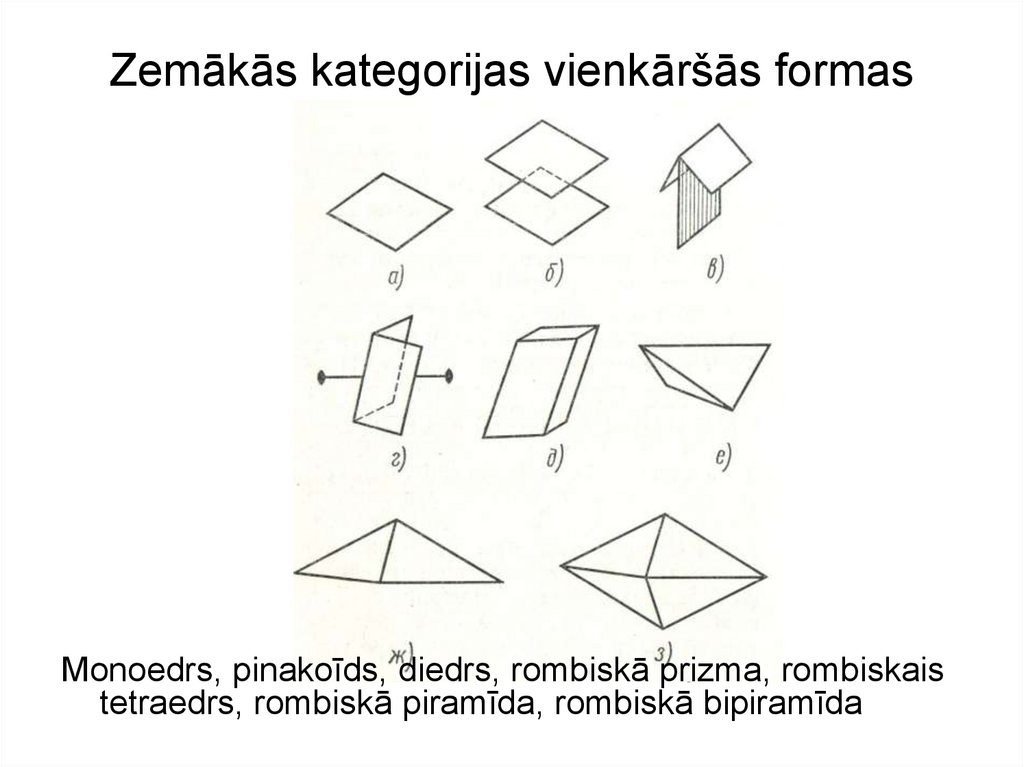
5. Zemākās kategorijas vienkāršās formas

Monoedrs, pinakoīds, diedrs, rombiskā prizma, rombiskais
tetraedrs, rombiskā piramīda, rombiskā bipiramīda

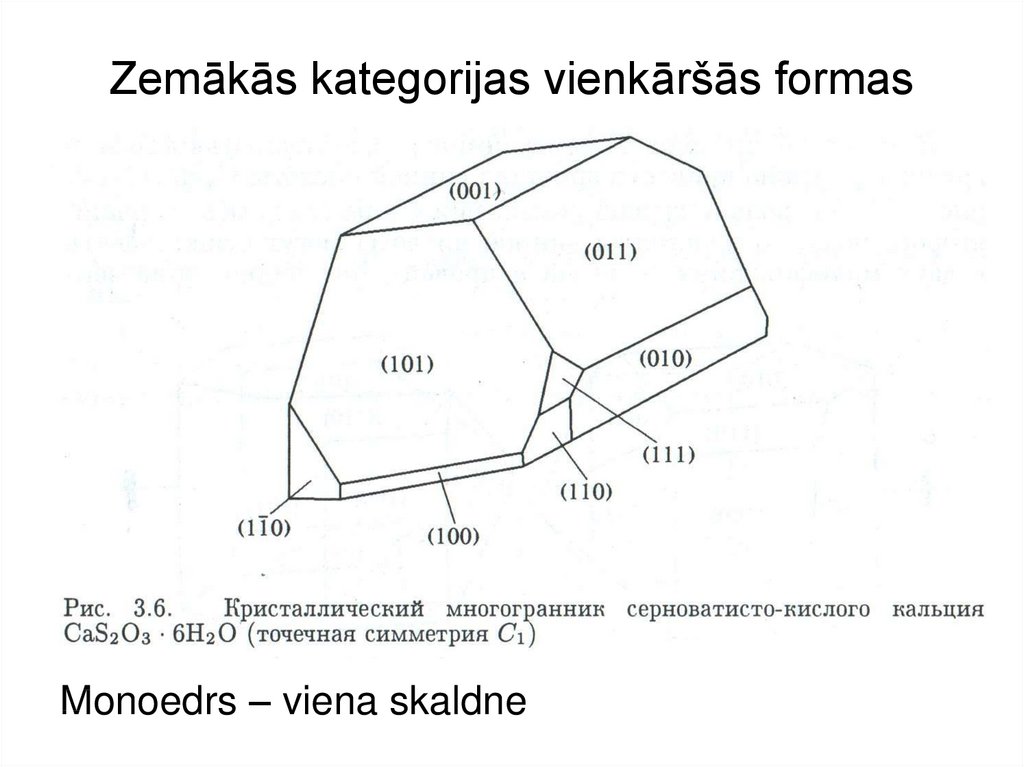
6. Zemākās kategorijas vienkāršās formas

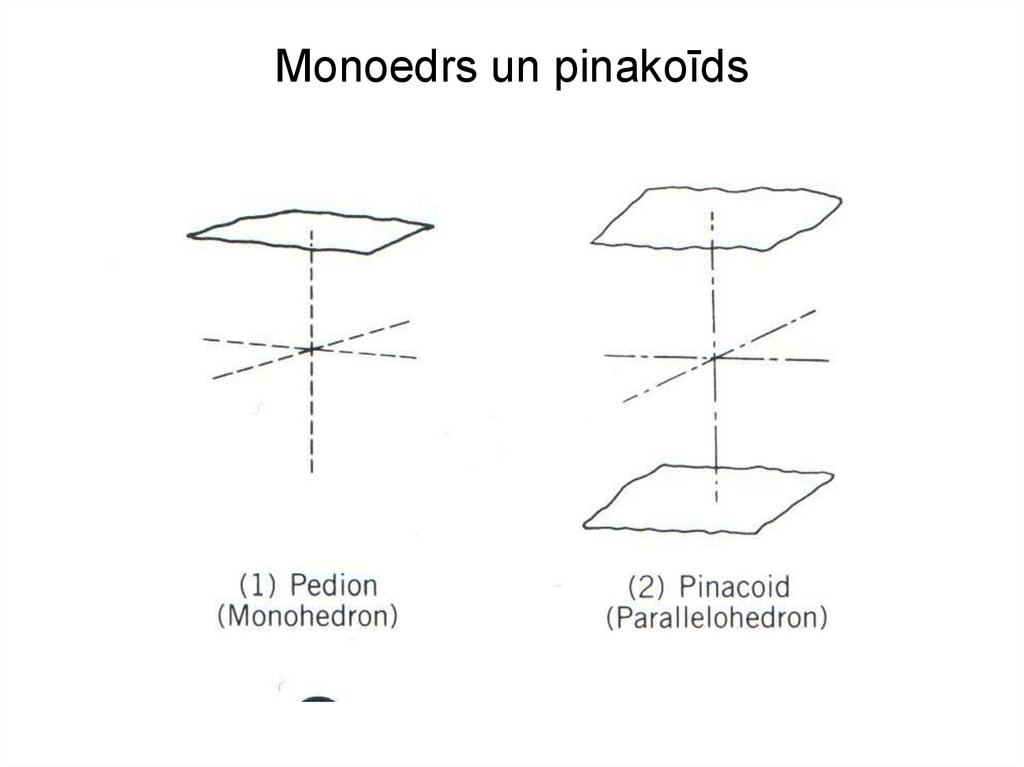
Monoedrs – viena skaldne

7. Monoedrs un pinakoīds

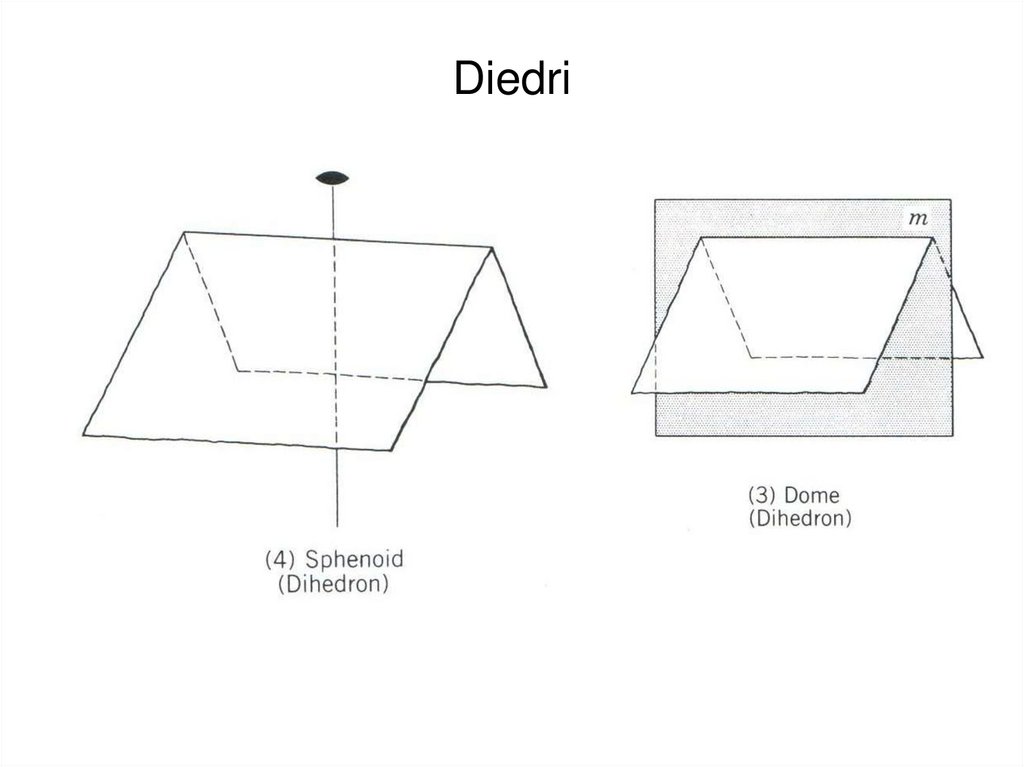
8. Diedri

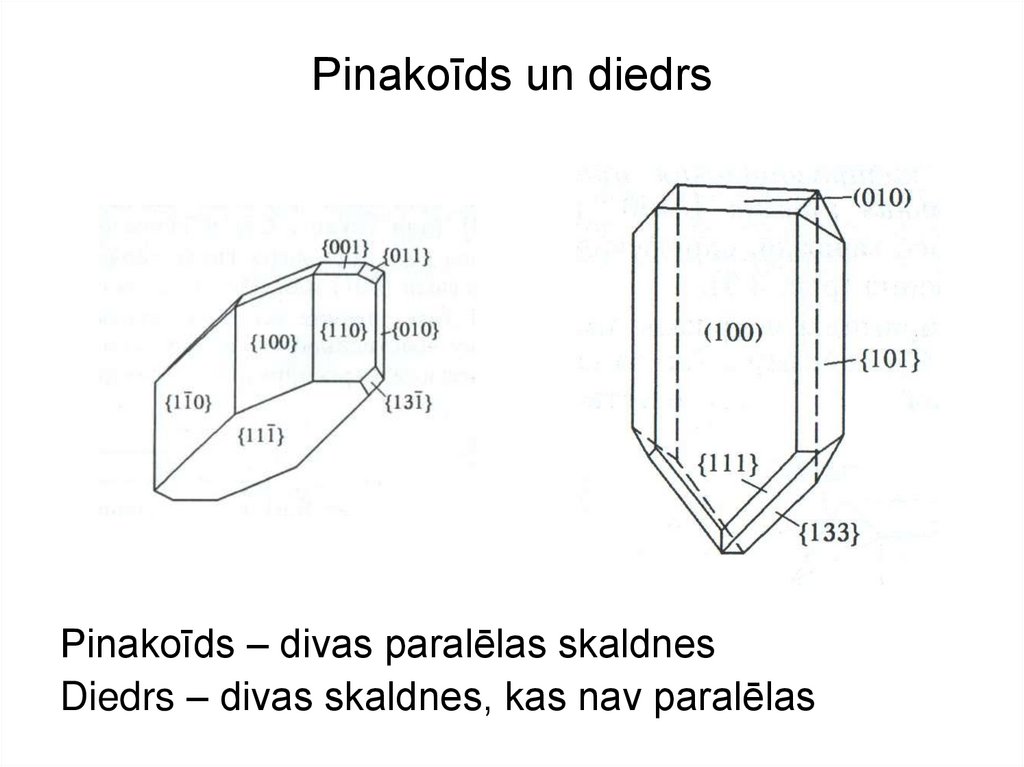
9. Pinakoīds un diedrs

Pinakoīds – divas paralēlas skaldnes
Diedrs – divas skaldnes, kas nav paralēlas

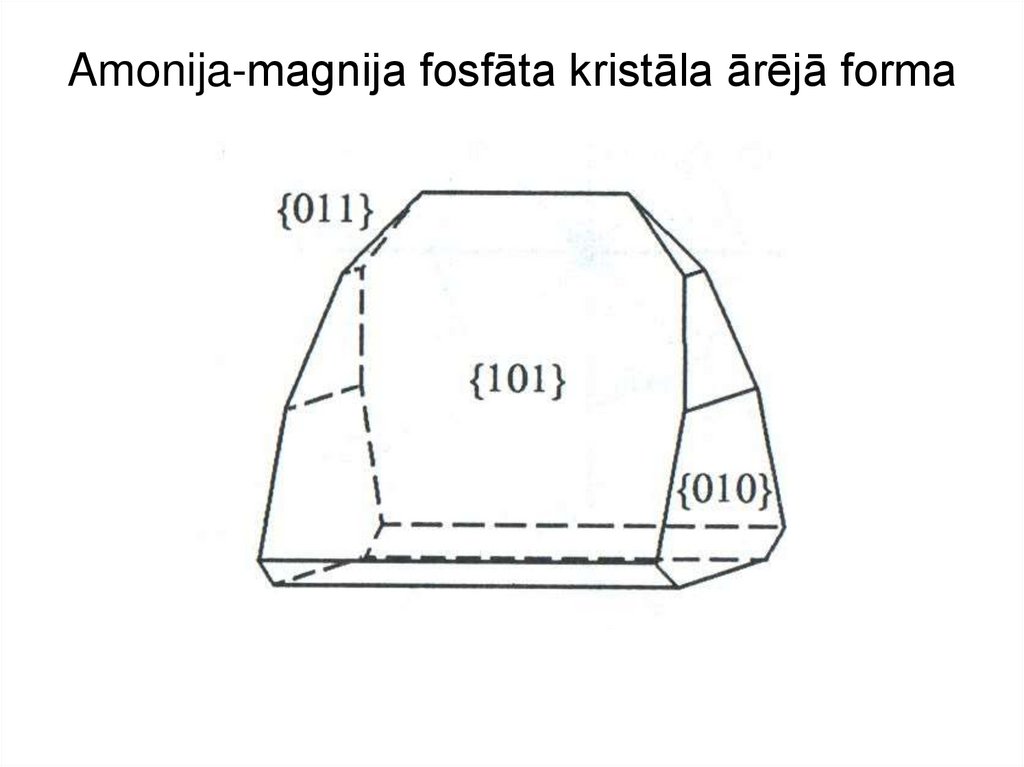
10. Amonija-magnija fosfāta kristāla ārējā forma

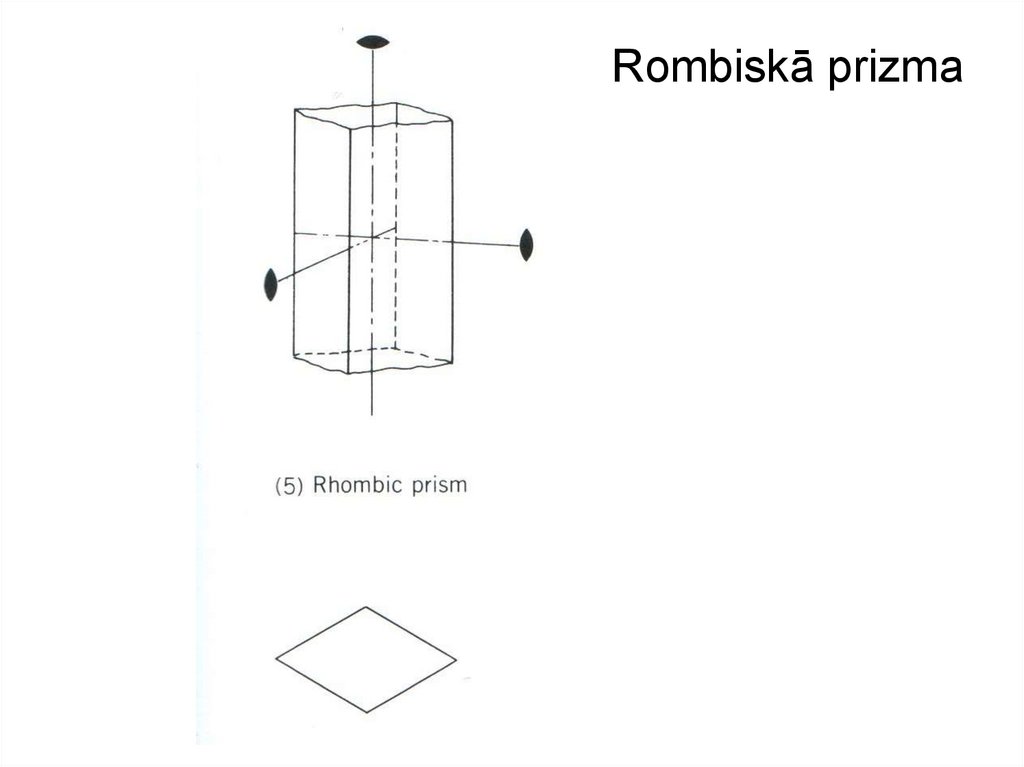
11. Rombiskā prizma

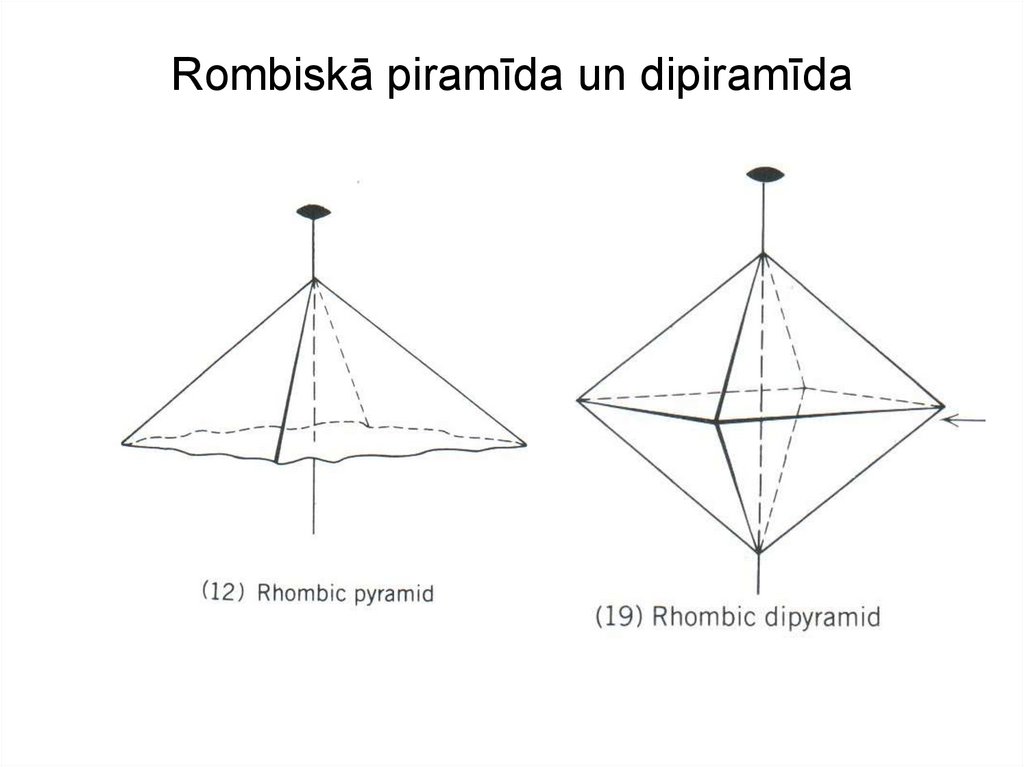
12. Rombiskā piramīda un dipiramīda

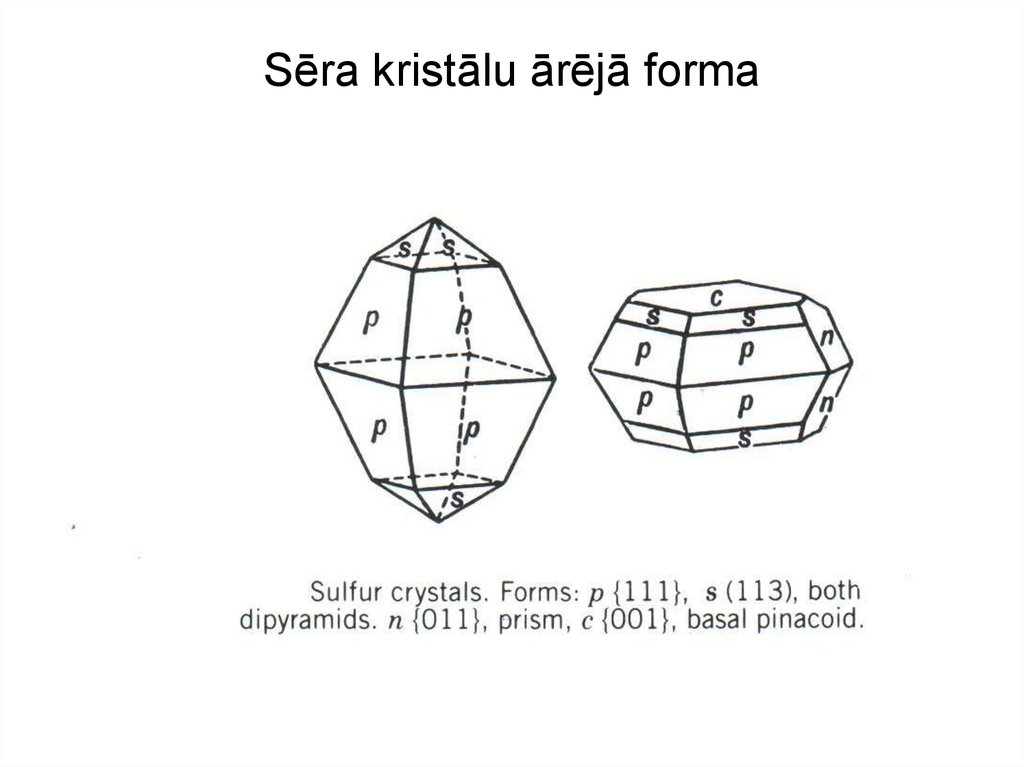
13. Sēra kristālu ārējā forma

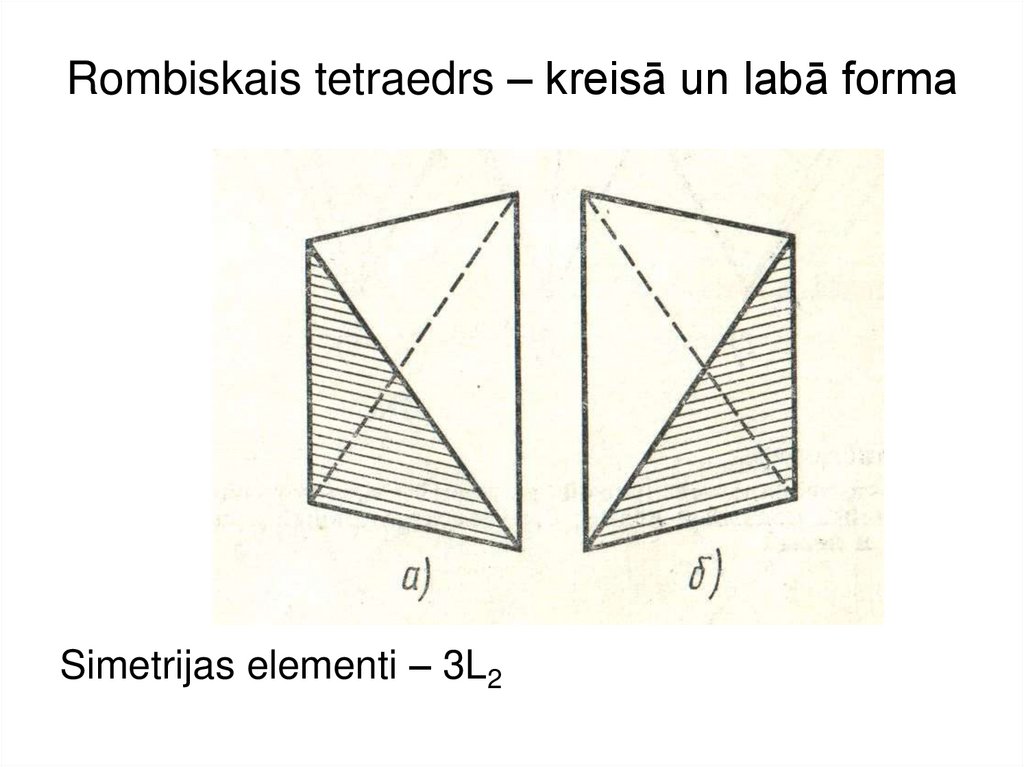
14. Rombiskais tetraedrs – kreisā un labā forma

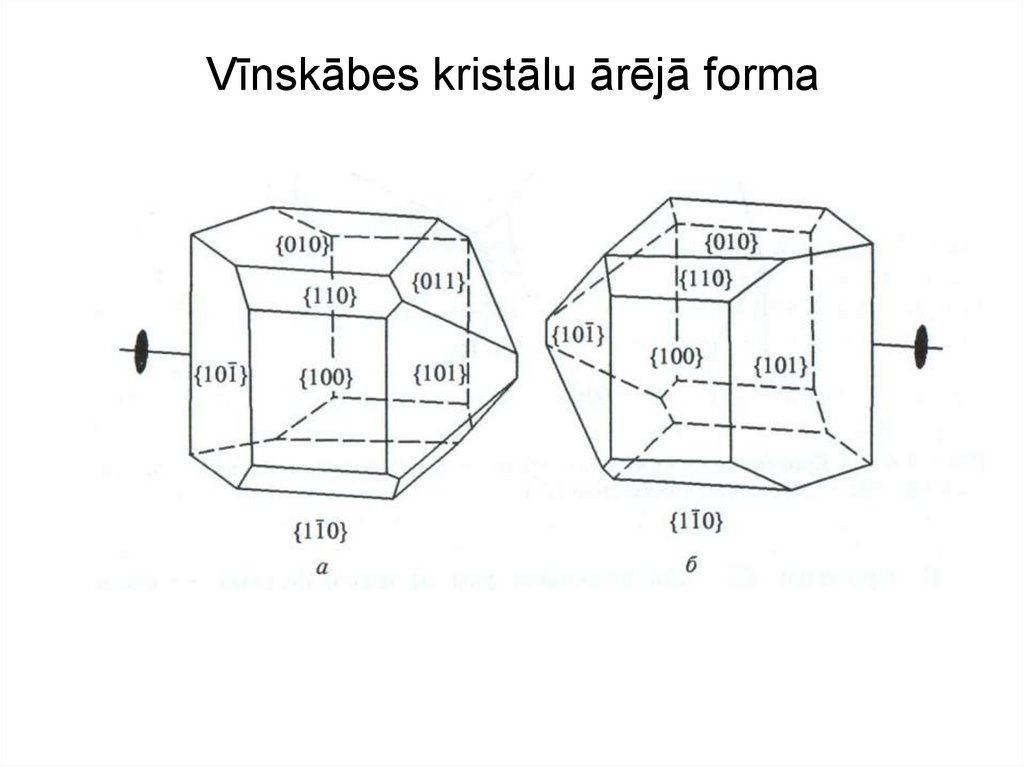
Simetrijas elementi – 3L2

15. Vīnskābes kristālu ārējā forma

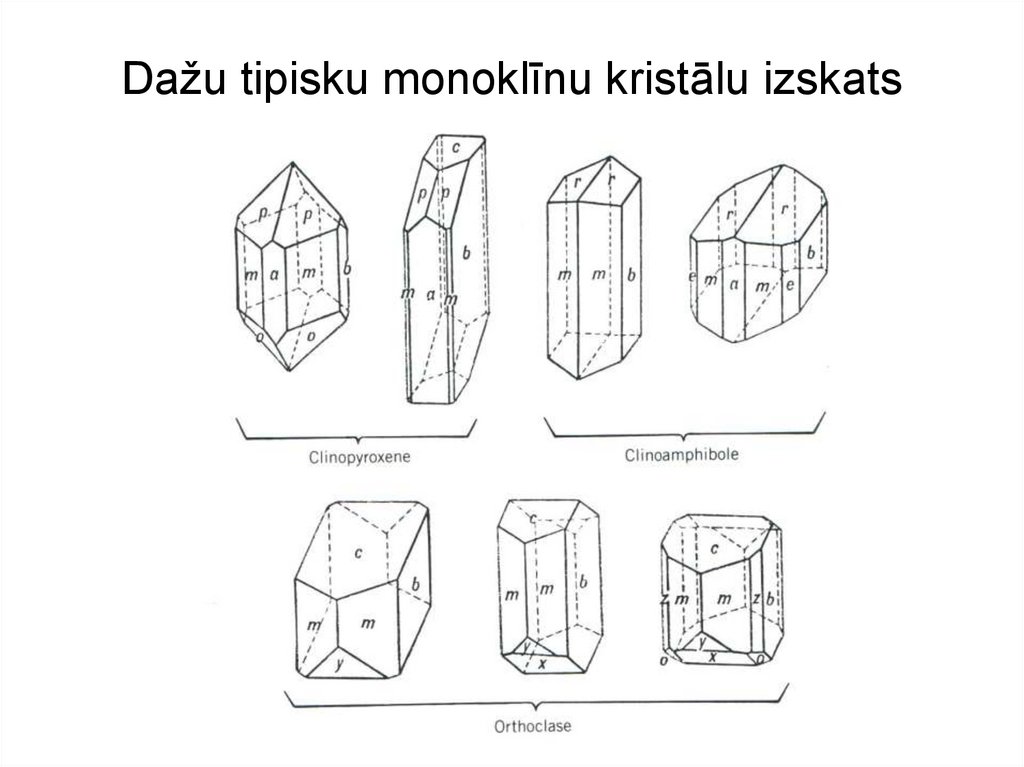
16. Dažu tipisku monoklīnu kristālu izskats

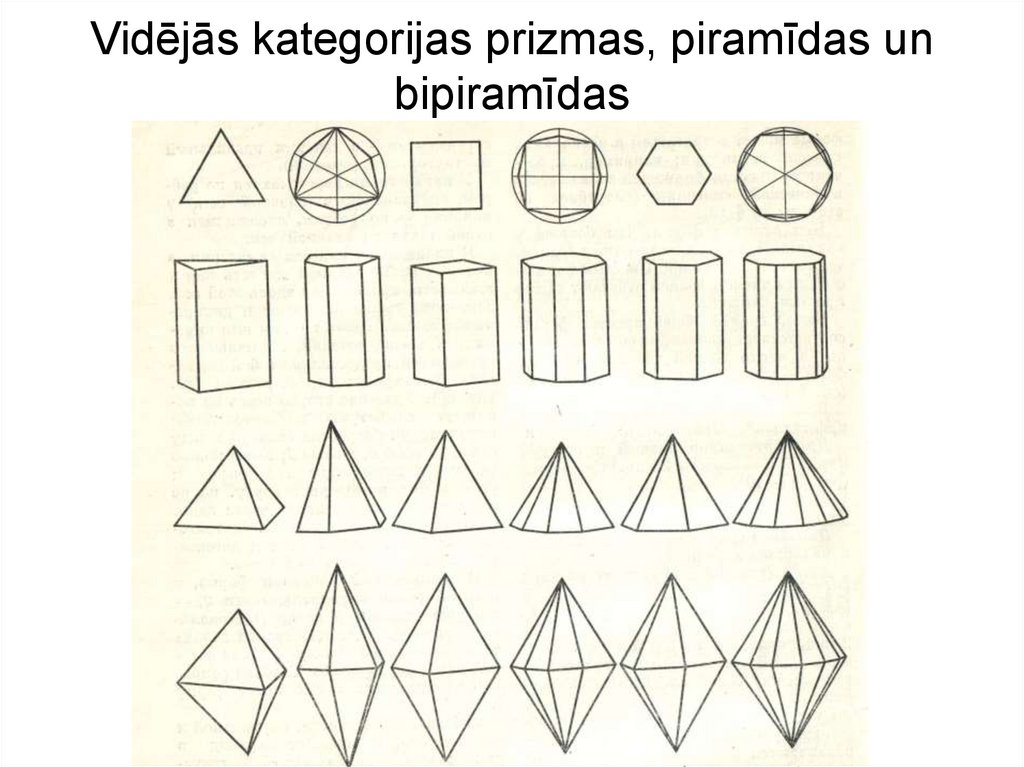
17. Vidējās kategorijas vienkāršās formas

18. Vidējās kategorijas prizmas, piramīdas un bipiramīdas

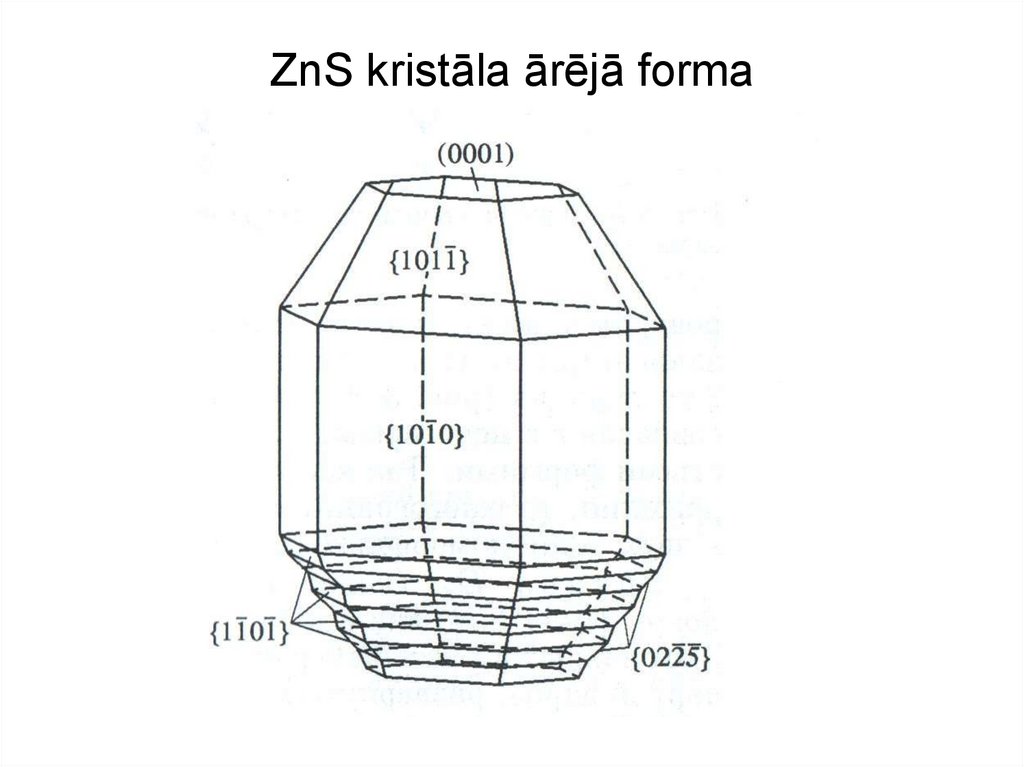
19. ZnS kristāla ārējā forma

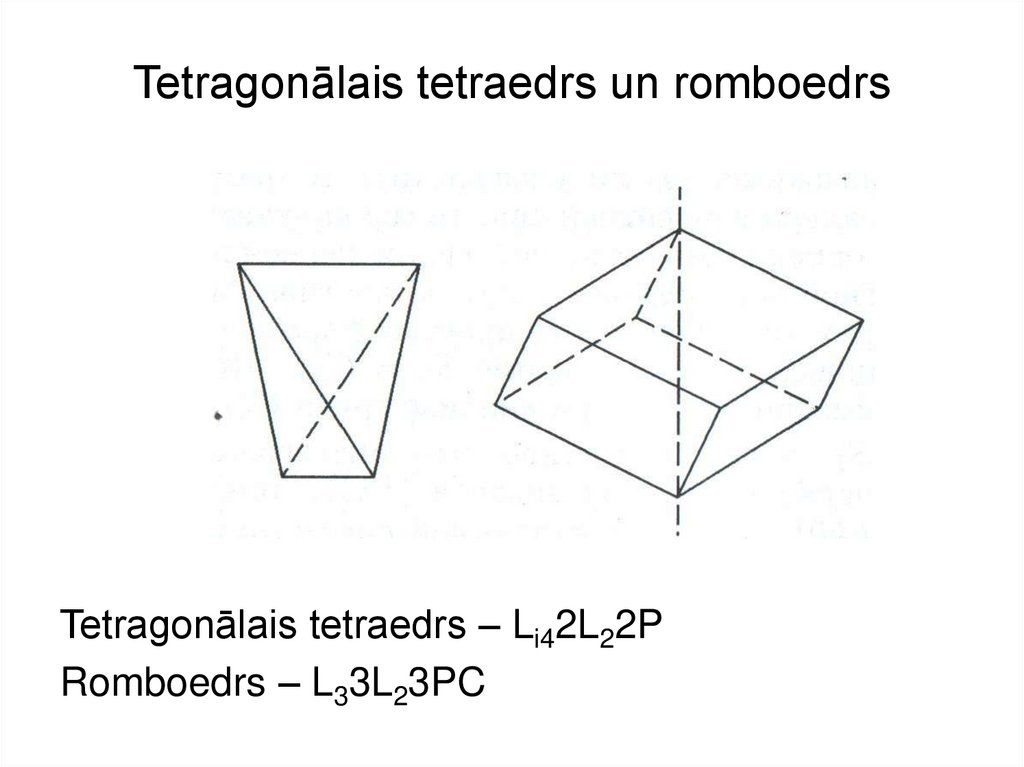
20. Tetragonālais tetraedrs un romboedrs

Tetragonālais tetraedrs – Li42L22P
Romboedrs – L33L23PC

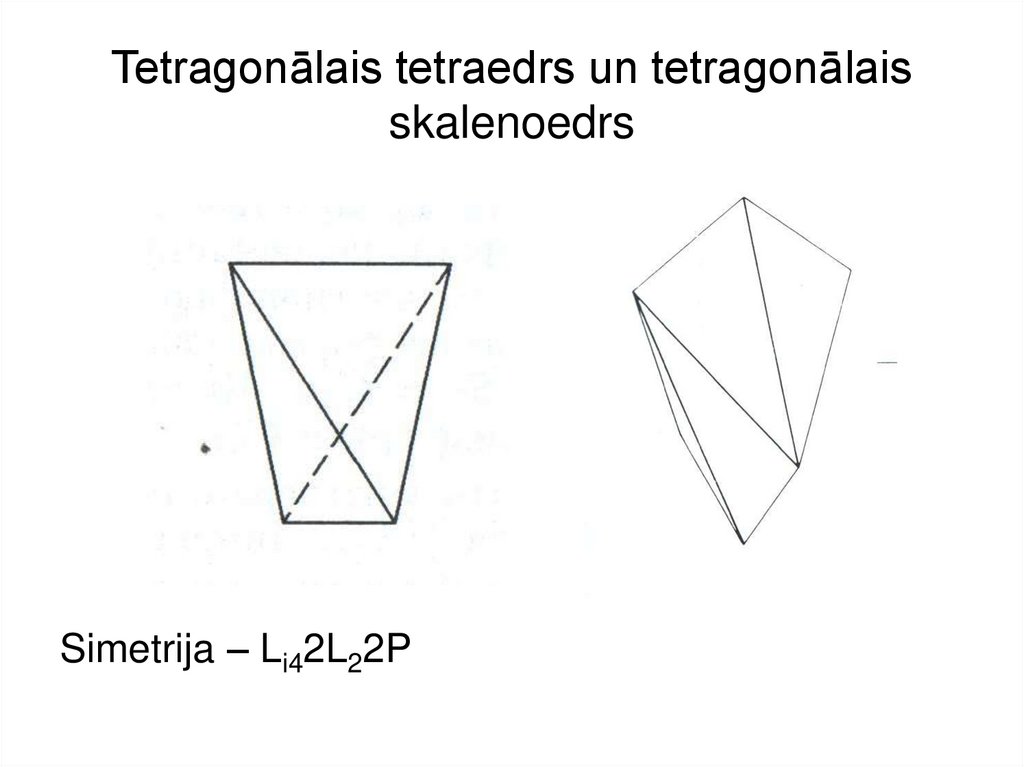
21. Tetragonālais tetraedrs un tetragonālais skalenoedrs

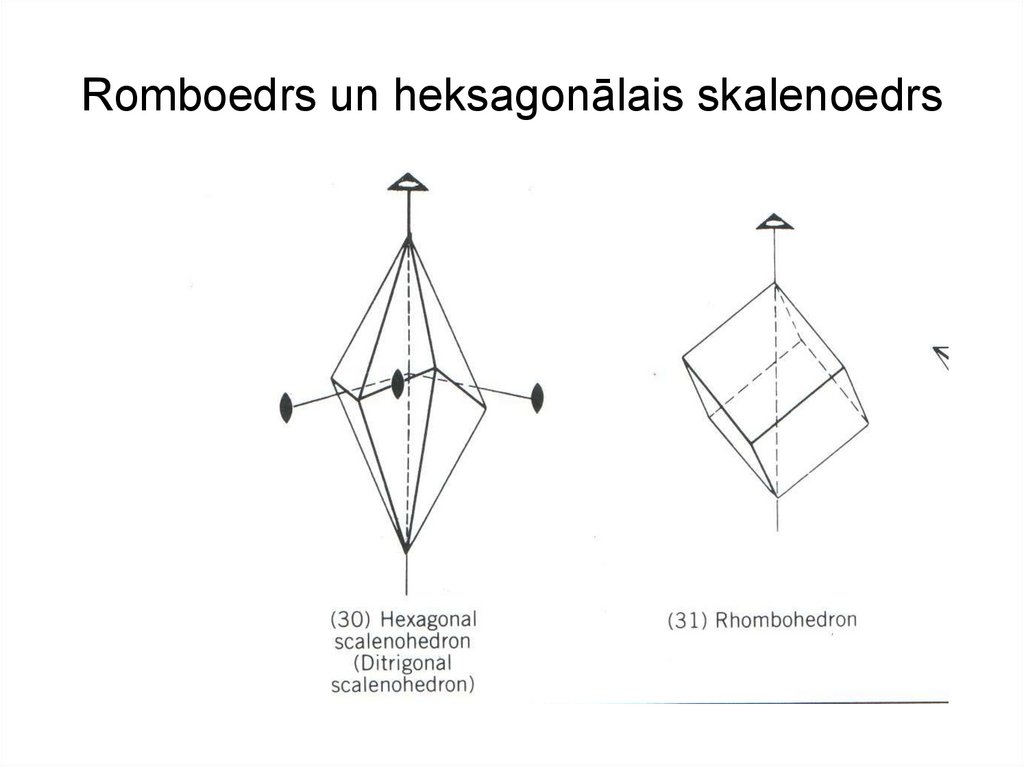
Simetrija – Li42L22P

22. Romboedrs un heksagonālais skalenoedrs

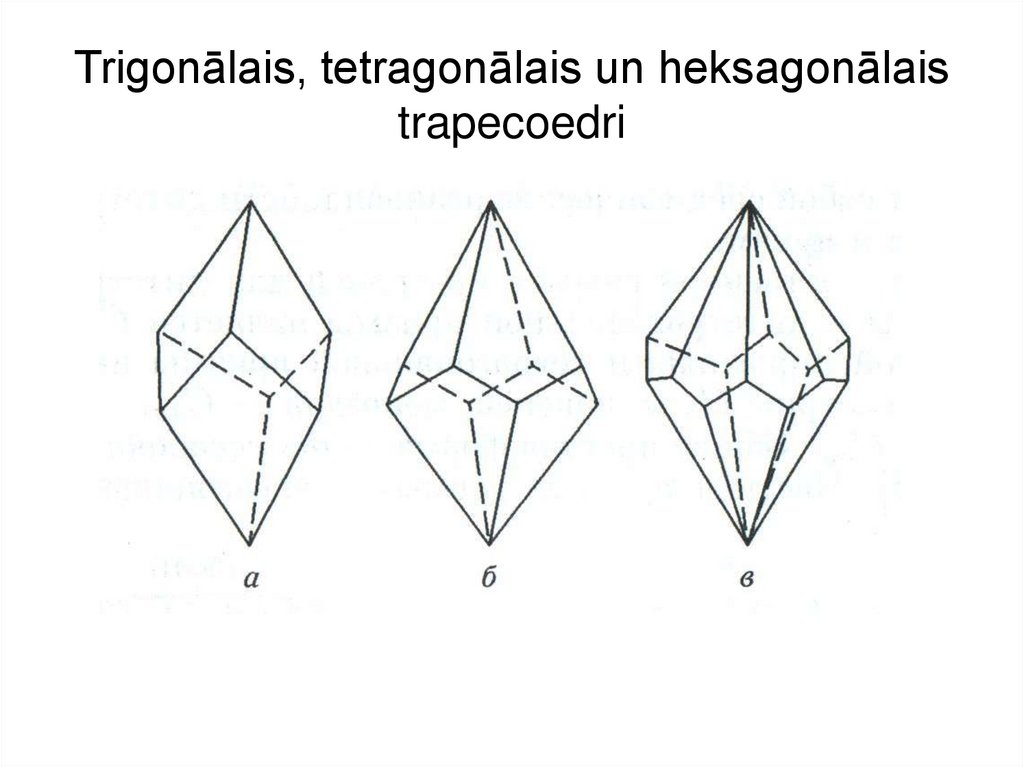
23. Trigonālais, tetragonālais un heksagonālais trapecoedri

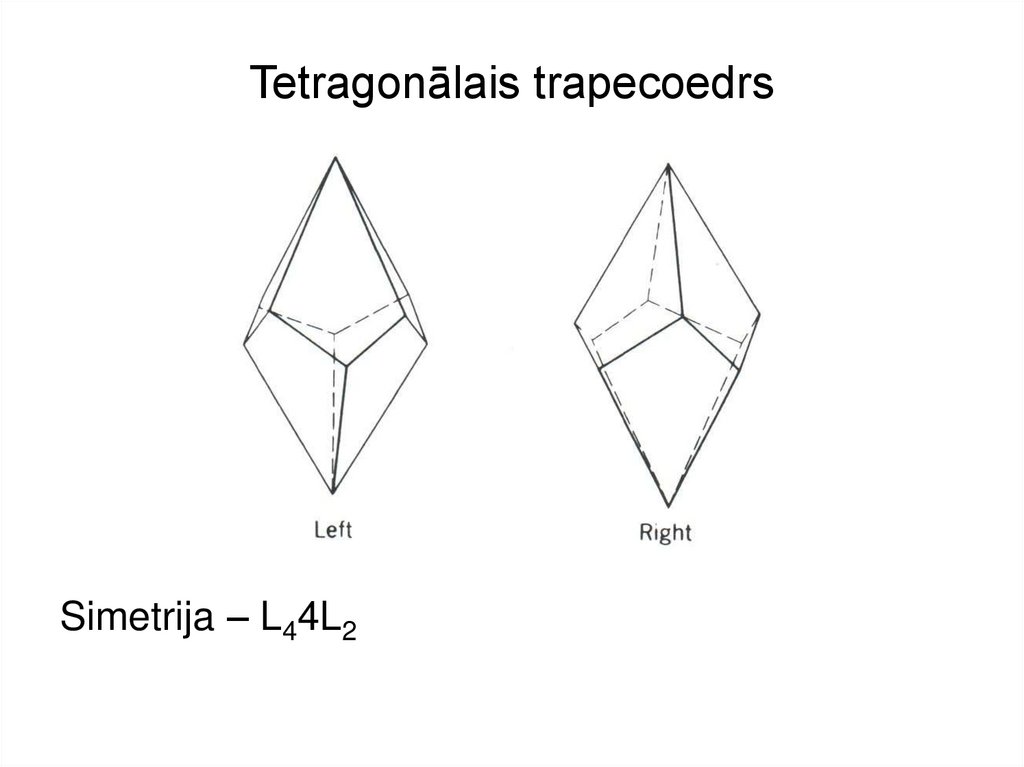
24. Tetragonālais trapecoedrs

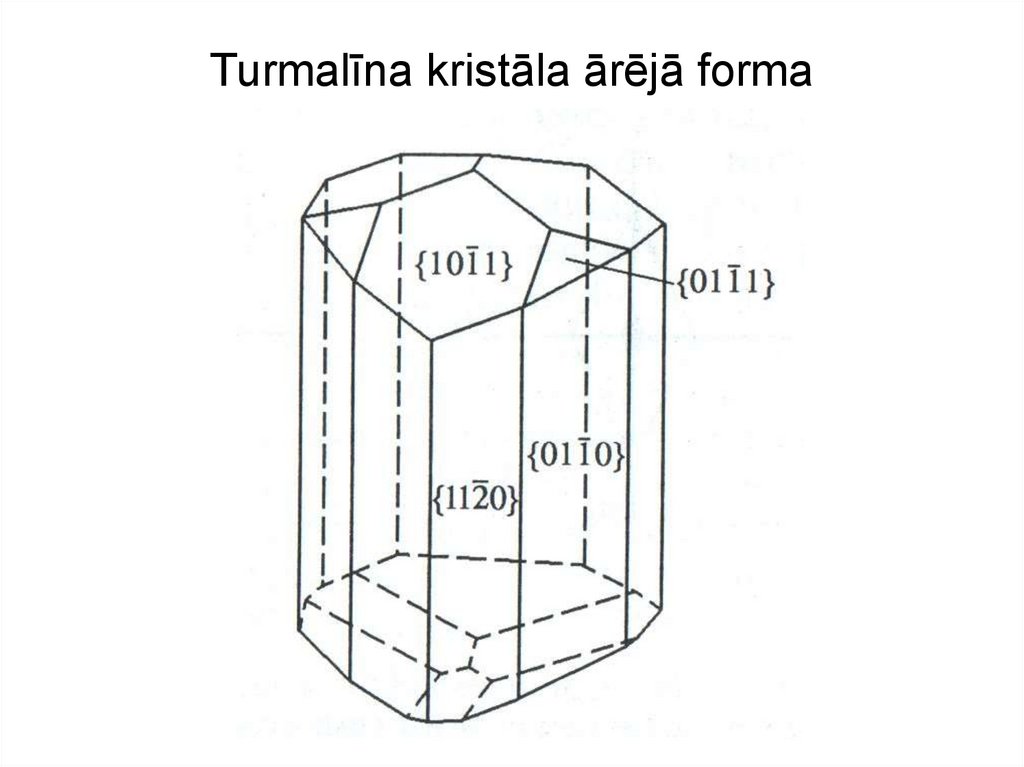
Simetrija – L44L2

25. Turmalīna kristāla ārējā forma

26. Aragonīta kristāla ārējā forma

27. Kombinācijas

Kā noteikt vienkāršo formu?
Vienādo skaldņu skaits
To savstarpējais novietojums
Sadalījums pa simetrijas grupām

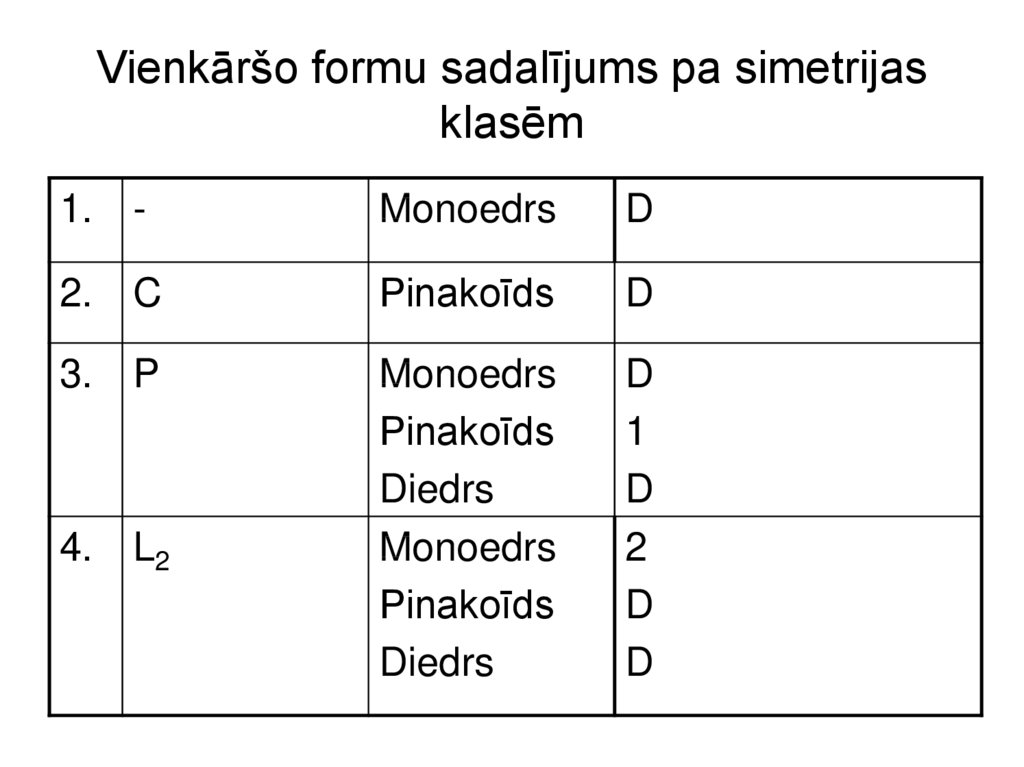
28. Vienkāršo formu sadalījums pa simetrijas klasēm

1. -
Monoedrs
D
2. C
Pinakoīds
D
3. P
Monoedrs
Pinakoīds
Diedrs
Monoedrs
Pinakoīds
Diedrs
D
1
D
2
D
D
4. L2

29. Vienkāršo formu sadalījums pa simetrijas klasēm

5. L2PC
6. L22P
7. 3L2
Pinakoīds
Rombiskā prizma
Monoedrs
Pinakoīds
Diedrs
Rombiskā prizma
Rombiskā piramīda
Pinakoīds
Rombiskā prizma
Rombiskais tetraedrs
D
D
2
2
D
D
D
3
D
D

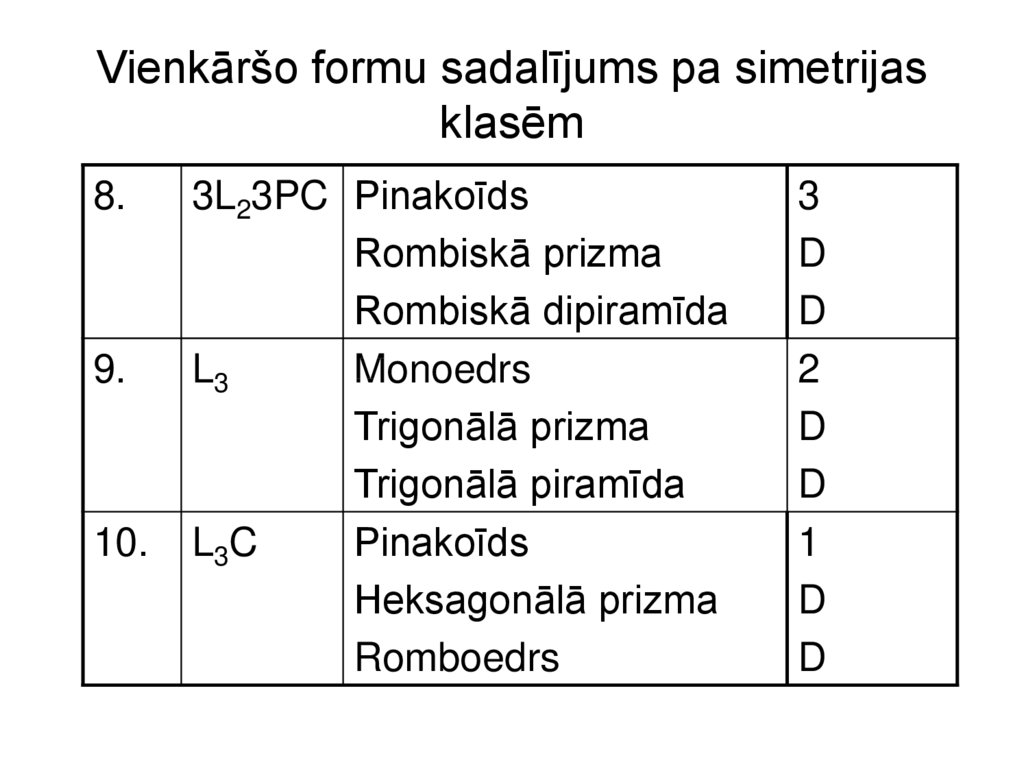
30. Vienkāršo formu sadalījums pa simetrijas klasēm

8.
9.
10.
3L23PC Pinakoīds
Rombiskā prizma
Rombiskā dipiramīda
L3
Monoedrs
Trigonālā prizma
Trigonālā piramīda
L 3C
Pinakoīds
Heksagonālā prizma
Romboedrs
3
D
D
2
D
D
1
D
D

31. Vienkāršo formu sadalījums pa simetrijas klasēm

11.
L33P
Monoedrs
Trigonālā prizma
Ditrigonālā prizma
Heksagonālā prizma
Trigonālā piramīda
Heksagonālā piramīda
Ditrigonālā piramīda
2
2
D
1
D
D
D

32. Vienkāršo formu sadalījums pa simetrijas klasēm

12. L33L2
Pinakoīds
Trigonālā prizma
Ditrigonālā prizma
Heksagonālā prizma
Trigonālā dipiramīda
Romboedrs
Trigonālais trapecoedrs
1
2
D
1
D
D
D

33. Vienkāršo formu sadalījums pa simetrijas klasēm

13.
14.
L33L23PC Pinakoīds
Heksagonālā prizma
Diheksagonālā prizma
Heksagonālā dipiramīda
Romboedrs
Trigonālais skalenoedrs
L4
Monoedrs
Tetragonālā prizma
Tetragonālā piramīda
1
2
D
D
D
D
2
D
D

34. Vienkāršo formu sadalījums pa simetrijas klasēm

15.
L4PC
16.
L44P
Pinakoīds
Tetragonālā prizma
Tetragonālā dipiramīda
Monoedrs
Tetragonālā prizma
Ditetragonālā prizma
Tetragonālā piramīda
Ditetragonālā piramīda
1
D
D
2
2
D
D
D

35. Vienkāršo formu sadalījums pa simetrijas klasēm

17.
18.
Pinakoīds
Tetragonālā prizma
Ditetragonālā prizma
Tetragonālā dipiramīda
Tetragonālais trapecoedrs
L44L2PC Pinakoīds
Tetragonālā prizma
Ditetragonālā prizma
Tetragonālā dipiramīda
Ditetragonālā dipiramīda
L44L2
1
2
D
D
D
1
2
D
D
D

36. Vienkāršo formu sadalījums pa simetrijas klasēm

19.
20.
Pinakoīds
Tetragonālā prizma
Tetragonālais tetraedrs
Li42L22P Pinakoīds
Tetragonālā prizma
Ditetragonālā prizma
Tetragonālā dipiramīda
Tetragonālais tetraedrs
Tetragonālais skalenoedrs
Li4
1
D
D
1
2
D
D
D
D

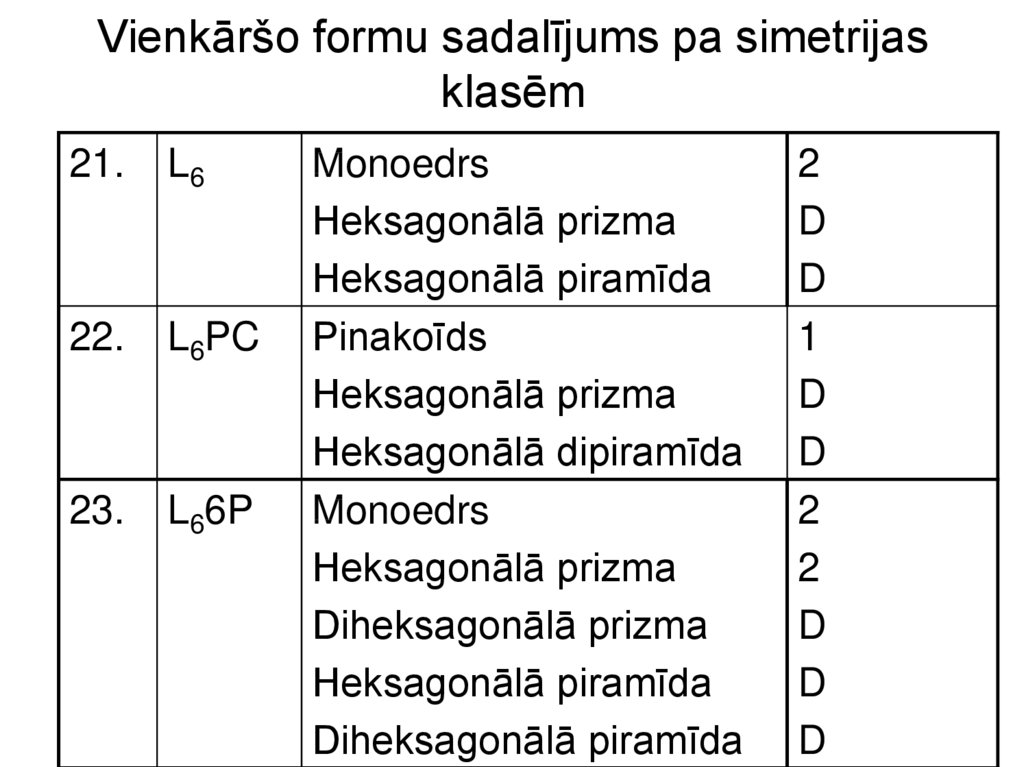
37. Vienkāršo formu sadalījums pa simetrijas klasēm

21.
L6
22.
L6PC
23.
L66P
Monoedrs
Heksagonālā prizma
Heksagonālā piramīda
Pinakoīds
Heksagonālā prizma
Heksagonālā dipiramīda
Monoedrs
Heksagonālā prizma
Diheksagonālā prizma
Heksagonālā piramīda
Diheksagonālā piramīda
2
D
D
1
D
D
2
2
D
D
D

38. Vienkāršo formu sadalījums pa simetrijas klasēm

24.
25.
Pinakoīds
Heksagonālā prizma
Diheksagonālā prizma
Heksagonālā dipiramīda
Heksagonālais trapecoedrs
L66L27PC Pinakoīds
Heksagonālā prizma
Diheksagonālā prizma
Heksagonālā dipiramīda
Diheksagonālā dipiramīda
L66L2
1
2
D
D
D
1
2
D
D
D

39. Vienkāršo formu sadalījums pa simetrijas klasēm

26. Li6
(L3P)
27. Li63L23P
(L33L24P)
Pinakoīds
Trigonālā prizma
Trigonālā dipiramīda
Pinakoīds
Trigonālā prizma
Ditrigonālā prizma
Heksagonālā prizma
Trigonālā dipiramīda
Heksagonālā dipiramīda
Ditrigonālā dipiramīda
1
D
D
1
2
D
1
D
D
D

40. Vienkāršo formu sadalījums pa simetrijas klasēm

28.
4L33L2
Heksaedrs
Rombododekaedrs
Pentagondodekaedrs
Tetraedrs
Trigontritetraedrs
Tetragontritetraedrs
Pentagontritetraedrs
1
1
D
2
D
D
D

41. Vienkāršo formu sadalījums pa simetrijas klasēm

29.
3L24L33PC Heksaedrs
Rombododekaedrs
Pentagondodekaedrs
Oktaedrs
Tetragontrioktaedrs
Trigontrioktaedrs
Didodekaedrs
1
1
D
1
D
D
D

42. Vienkāršo formu sadalījums pa simetrijas klasēm

30.
3Li44L36P
(3L24L36P)
Heksaedrs
Rombododekaedrs
Tetraheksaedrs
Tetraedrs
Trigontritetraedrs
Teragontritetraedrs
Heksatetraedrs
1
1
D
2
D
D
D

43. Vienkāršo formu sadalījums pa simetrijas klasēm

31.
3L44L36L2
Heksaedrs
Rombododekaedrs
Tetraheksaedrs
Oktaedrs
Tetragontrioktaedrs
Trigontrioktaedrs
Pentagontrioktaedrs
1
1
D
1
D
D
D

44. Vienkāršo formu sadalījums pa simetrijas klasēm

32.
3L44L36L29PC Heksaedrs
Rombododekaedrs
Tetraheksaedrs
Oktaedrs
Tetragontrioktaedrs
Trigontrioktaedrs
Pentagontrioktaedrs
1
1
D
1
D
D
D