Задачи на построение. Окружность. Урок 1

1.

Урок 1
01.03.2019

2.

Самостоятельная работа
Вариант I
1. Докажите равенство треугольников
АВЕ и DСЕ на рисунке 1, если АЕ = ЕD,
А = D.
Найдите стороны треугольника АВЕ,
если DЕ = 3 см, ДС = 4 см, ЕС = 5 см.
Рис. 1
2. На рисунке 2 АВ = АD, ВС =
= СD. Докажите, что луч АС –
биссектриса угла ВАD.
В а р и а н т II
1.
Докажите
равенство
треугольников МОN и РОN на
рисунке 3, если МОN = РОN, а
луч NO – биссектриса МNР.
Найдите углы треугольника NOР,
если МNО = 28°, NМО = 42°,
NОМ = 110°.
Рис. 2
Рис. 3
2. На рисунке 4 DЕ = DК, СЕ =
= СК. Докажите, что луч СD –
биссектриса угла ЕСК.
Рис. 4
2

3.

Определение
Предложение, в котором разъясняется
смысл того или иного выражения или
названия, называется определением.
Мы уже встречались с определениями,
например с определением угла, смежных
углов, равнобедренного треугольника и т. д.
Дадим определение еще одной
геометрической фигуры — окружности.
3

4.

Определение окружности
Окружностью называется геометрическая
фигура, состоящая из всех точек плоскости,
расположенных на заданном расстоянии от
данной точки.
Данная точка называется центром
окружности, а отрезок, соединяющий
центр с какой-либо точкой
окружности, - радиусом окружности.
Из определения окружности следует,
что все радиусы имеют одну и ту же
длину.
4

5.

Отрезок, соединяющий две
точки окружности,
называется ее хордой.
Хорда, проходящая через
центр окружности,
называется диаметром.
На рисунке отрезки АВ и EF —
хорды окружности, отрезок CD —
диаметр окружности. Очевидно,
диаметр окружности в два раза
больше ее радиуса. Центр
окружности является серединой
любого диаметра.
5

6.

Любые две точки
окружности делят ее на две
части. Каждая из этих частей
называется дугой
окружности. На рисунке ALB
и AM В - дуги, ограниченные
точками А и В.

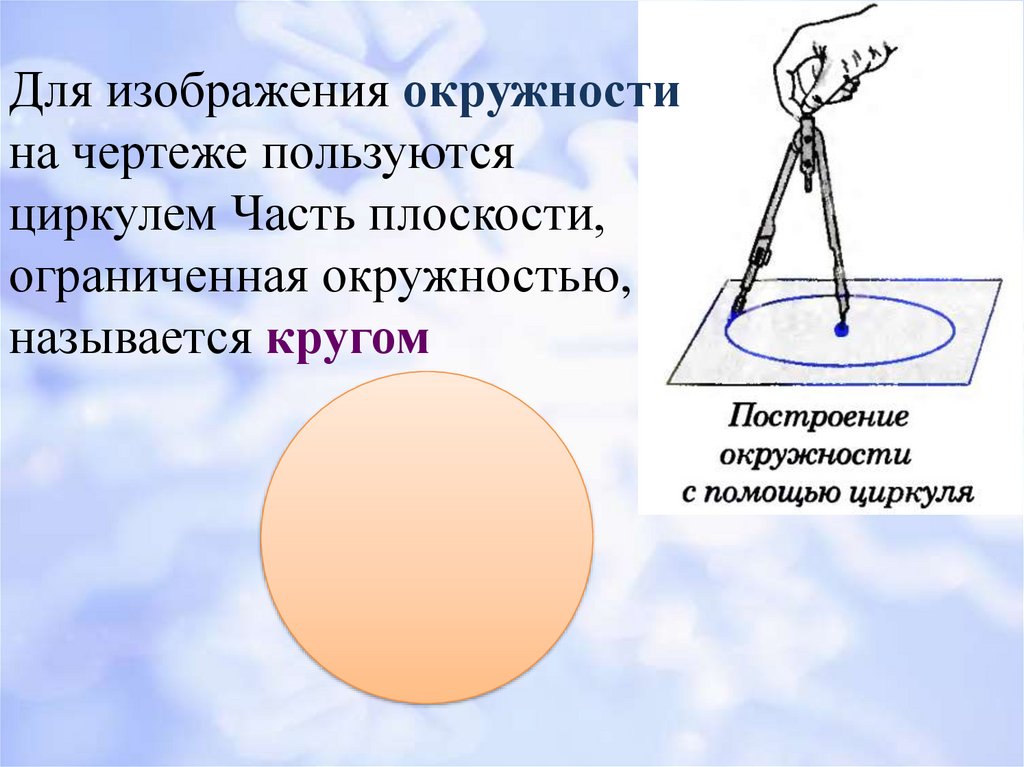
7.

Для изображения окружности
на чертеже пользуются
циркулем Часть плоскости,
ограниченная окружностью,
называется кругом

8.

Упражнения
1. № 143 (устно).
2. № 146.

9.

Упражнения
Рассмотрим треугольник ВОС и треугольник DОА:
АО = ОВ = ОС = ОD (радиусы окружности); ВОС = DОА (вертикальные
углы равны), тогда ВОС = DОА (первый признак, по двум сторонам и углу
между ними).
Значит, АD = СВ = 13 см, АО = ОВ = ОD = 16 : 2 = 8 (см); тогда Р DОА =
АD + АО + ОD = 13 + 8 + 8 = 29 (см).
C
О т в е т : 29 см.
А
О
D
В

10.

Самостоятельная работа
Вариант I
Отрезки KМ и ЕF являются диаметрами окружности с центром О. Докажите, что:
а) FEM = KМЕ; б) отрезки KЕ и МF равны.
В а р и а н т II
Отрезки МЕ и РK являются диаметрами окружности с центром О. Докажите, что:
а) EMР = МРK; б) отрезки МK и РЕ равны.
В а р и а н т III
В окружности с центром О проведены диаметр АС и радиус ОВ так, что хорда ВС
равна радиусу. Найти АОВ, если ВСО = 60°.
В а р и а н т IV
В окружности с центром О проведены хорды АВ и СD. Докажите, что АВ = СD,
если АОС = ВОD.

11.

Задание на с/п:
Изучить п. 21 из § 4; ответить на вопрос
16 на с. 50; решить задачи №№ 145, 162.
Обязательно принести на следующий урок
циркули и линейки.

12.

Синквейн
Окружность
Круглая, имеющая центр, радиус, диаметр, хорду,
Берем циркуль, чертим, отмечаем центр
все точки равноудаленные от данной точки
плоскости
Похожа на обруч!